Cybernetics and Systems, Vol.30 (1999), No.6, pp.571-585.
© A.P.Levich, A.V.Solov'yov
CATEGORY-FUNCTOR MODELLING OF NATURAL SYSTEMS
A. P. LEVICH, A. V. SOLOV'YOV
ABSTRACT
An approach to the derivation of dynamic equations for natural systems modelled by mathematical structures is suggested. The approach rests on an extremum principle which postulates that among all possible states of a system those ones are actually realized which correspond to an extremal (in a rigorous mathematical sense) structure. The suggested method of ordering the structured sets with the aid of category and functor theory generalizes the cardinality ordering of structureless sets. The method makes it possible to determine the functionals for the variational problem which describes a system under study. The approach is illustrated by a model of an ecological community.
INTRODUCTION
A theoretical description of any natural system includes two important aspects at least. First, one should construct a concrete mathematical model of both the admissible states of the system and its transitions between these states. Second, one should establish the choice rules (often in the form of an extremum principle) selecting, among the many theoretically admissible states of the system, only those states which are realized in nature under the given external conditions. In the present paper, we suggest that both these problems be solved by the methods of category theory.
Apparently, the first to widely use set theory and topology for modelling the biological processes was Rashevsky (1954, 1955) laying the foundations of abstract biology. Later, in his works on relational biology, Rosen (1958, 1959) made the next step and applied category theory to the description of biological systems, in particular, a living cell. In subsequent years, an abstract category-theoretic approach to problems of mathematical biology was developed in various ways among which we would like to note primarily: the molecular set theory (Bartholomay, 1960, 1965), the organismic supercategories (Baianu, 1968, 1970), and the energy theory of abstract ecological systems (Leguizamon, 1975, 1993).
In this work, we have attempted to construct a category-functor model of abstract natural systems (not necessarily biological) and to apply it to the description of ecological communities. The paper contains a development of ideas presented in Levich (1982).
A CATEGORY-THEORETIC MODEL OF NATURAL SYSTEMS
An analysis shows that, in all practically interesting cases, an arbitrary state or even the whole state space of a natural system can be identified with a set equipped with a certain mathematical structure: algebraic, topological, etc.
For example, it is convenient to describe a state of an ecological community by means of a set with a partition into mutually disjoint classes where elements of the set are organisms forming the community, while partition classes are populations of biological species (Levich, 1982). Below, we will illustrate the basic statements of the general theory with the ecological community example.
Returning to an arbitrary natural system, we note that a mathematical structure, specified on sets-states, models only those properties of the real system which are invariant under its transitions from one admissible state to any other. Precisely such a property is the existence of a species structure in an ecological community. Thus, in the general case, the state space of a natural system is simply a class of uniformly structured sets (such as groups, topological spaces, sets with partitions, etc.).
Let A and B be two uniformly structured sets. Consider their direct product ![]() and fix a certain subset in it. Any subset
and fix a certain subset in it. Any subset ![]() is called a correspondence from A to B. In this connection, one uses the following notation:
is called a correspondence from A to B. In this connection, one uses the following notation: ![]() for the complete image of the element
for the complete image of the element ![]() with respect to the correspondence
with respect to the correspondence ![]() and
and ![]() for the complete preimage of the element
for the complete preimage of the element ![]() with respect to the same correspondence. Situations are possible when
with respect to the same correspondence. Situations are possible when ![]() or/and
or/and ![]() for certain a and b. Let us list the most important types of correspondences from A to B:
for certain a and b. Let us list the most important types of correspondences from A to B:
Moreover, various combinations of types 1-4 are also admissible; in particular, everywhere defined functional correspondences which are identified with ordinary mappings. All of them will be needed below.
Following Levich (1982), we call correspondences preserving a mathematical structure specified on the sets A and B structure morphisms and denote them by Greek letters: ![]() For example, structure morphisms of sets with partitions are correspondences transforming each partition class of one set as a whole into some partition class of another set, so that different classes are transformed into different ones. Other examples of structure morphisms are homomorphisms of groups and continuous mappings of topological spaces.
For example, structure morphisms of sets with partitions are correspondences transforming each partition class of one set as a whole into some partition class of another set, so that different classes are transformed into different ones. Other examples of structure morphisms are homomorphisms of groups and continuous mappings of topological spaces.
According to the aforesaid, we will identify transitions between admissible states of an arbitrary natural system with corresponding structure morphisms. It is clear that each system is characterized by a specific class of structure morphisms reflecting its concrete “transitional” properties; even if two systems have the same state space, but distinct classes of structure morphisms, then one must distinguish such systems.
Thus, we suggest to associate with each natural system a mathematical construction S consisting of two classes: ![]() and
and ![]() . Here
. Here ![]() is a fixed class of uniformly structured sets which will be also called objects;
is a fixed class of uniformly structured sets which will be also called objects; ![]() is a fixed class of structure morphisms between these sets. It is not hard to see the following:
is a fixed class of structure morphisms between these sets. It is not hard to see the following:
Therefore, S is a category (Bucur & Deleanu, 1968; Goldblatt, 1979). Thus, the proposed model of natural systems has a simple category-theoretic interpretation according to which admissible states of a system are objects of the category S and permissible transitions between these states are morphisms of the category S.
In what follows, in general considerations, S will designate a category such that the class ![]() consists of all uniformly structured sets, while the class
consists of all uniformly structured sets, while the class ![]() consists of all structure morphisms between them.
consists of all structure morphisms between them.
A FUNCTOR METHOD OF COMPARISON OF STRUCTURED SETS AND AN EXTREMUM PRINCIPLE FOR NATURAL SYSTEMS
The next important step in describing a natural system is to establish an extremum principle selecting from the class of admissible states of the system only those states which are realized under the given external conditions. To this end, it is necessary to construct a function on the system state space taking values in a linearly ordered set (class) because the concept of “extreme state” is meaningful only in this case. The present section is devoted to a search for such a function defined on the class ![]() and having the most natural form from the viewpoint of category theory.
and having the most natural form from the viewpoint of category theory.
First of all, let us recall some information about cardinal numbers of nonstructured sets. Consider the category Set whose objects are arbitrary sets and morphisms are arbitrary correspondences between these sets. Below, we will call subclasses of the direct product ![]() binary relations on the class
binary relations on the class ![]() .
.
Let ![]() be the binary relation on
be the binary relation on ![]() defined by the rule:
defined by the rule:
![]() Û
there is an injective mapping of
Û
there is an injective mapping of ![]() into
into ![]() .
.
Here ![]() . It is obvious that
. It is obvious that ![]() has the following important properties:
has the following important properties:
i.e., ![]() is a preorder relation on
is a preorder relation on ![]() . We factorize this preorder by introducing the binary relation
. We factorize this preorder by introducing the binary relation ![]() on the same class
on the same class ![]() according to the rule:
according to the rule:
![]() Û
Û
![]() and
and ![]() .
.
It is not difficult to verify that the so defined relation ![]() is reflexive, transitive, and symmetric (the latter signifies that if
is reflexive, transitive, and symmetric (the latter signifies that if ![]() , then
, then ![]() as well). Therefore,
as well). Therefore, ![]() is an equivalence relation on
is an equivalence relation on ![]() . One can show (Levich, 1982) that
. One can show (Levich, 1982) that ![]() if and only if there exists a bijection between the sets
if and only if there exists a bijection between the sets ![]() and
and ![]() .
.
For each ![]() , we denote by
, we denote by ![]() the class of all the sets which are
the class of all the sets which are ![]() -equivalent to the set
-equivalent to the set ![]() , i.e.,
, i.e., ![]() . One usually calls this class the cardinal number of the set
. One usually calls this class the cardinal number of the set ![]() and writes
and writes ![]() (if
(if ![]() is a finite set, then
is a finite set, then ![]() is identified with the number of elements in
is identified with the number of elements in ![]() ). In other words, cardinal numbers of nonstructured sets are elements of the factor class
). In other words, cardinal numbers of nonstructured sets are elements of the factor class ![]() . We simultaneously have the canonical surjection
. We simultaneously have the canonical surjection ![]() ,
, ![]() .
.![]()
![]()
It is natural to define an order relation on the factor class ![]() , namely:
, namely:
![]() Û
Û
![]() .
.
The reflexivity and transitivity of ![]() follow from the corresponding properties of the preorder
follow from the corresponding properties of the preorder ![]() . The antisymmetry of
. The antisymmetry of ![]() is established by the simple reasoning:
is established by the simple reasoning: ![]() and
and ![]() Û
Û
![]() and
and ![]() Û
Û
![]() Þ
Þ
![]() . Thus,
. Thus, ![]() is indeed an order relation on
is indeed an order relation on ![]() and, moreover, this order is linear (i.e., any two cardinal numbers are comparable) (Bourbaki, 1960).
and, moreover, this order is linear (i.e., any two cardinal numbers are comparable) (Bourbaki, 1960).
Now, let us try to extend the above constructions to the case of the category S of uniformly structured sets. Let ![]() . By analogy with universal algebra, injective mappings of A into B (and vice versa) preserving a mathematical structure specified on these sets will be called structure monomorphisms.
. By analogy with universal algebra, injective mappings of A into B (and vice versa) preserving a mathematical structure specified on these sets will be called structure monomorphisms.
Consider the binary relation ![]() defined on the class
defined on the class ![]() by the following rule:
by the following rule:
![]() Û
there exists a structure monomorphism of A into B.
Û
there exists a structure monomorphism of A into B.
Evidently, the relation ![]() is reflexive and transitive; hence
is reflexive and transitive; hence ![]() is a preorder on
is a preorder on ![]() . Factorization of this preorder creates the equivalence relation
. Factorization of this preorder creates the equivalence relation ![]() on the same class
on the same class ![]() in the usual way:
in the usual way:
![]() Û
Û
![]() and
and ![]() .
.
For each ![]() , let us introduce the class
, let us introduce the class ![]() of uniformly structured sets which are
of uniformly structured sets which are ![]() -equivalent to A. Following Levich (1982), we call this class the structural number of the set A and use the notation
-equivalent to A. Following Levich (1982), we call this class the structural number of the set A and use the notation ![]() for it. Thus, by definition, structural numbers are elements of the factor class
for it. Thus, by definition, structural numbers are elements of the factor class ![]() . We simultaneously have the canonical surjection
. We simultaneously have the canonical surjection ![]() ,
, ![]() .
.
With the aid of ![]() one can define the order relation on the factor class
one can define the order relation on the factor class ![]() by setting
by setting
![]() .
.
The reflexivity, transitivity, and antisymmetry of ![]() are verified in an elementary way. However, unlike cardinal numbers, structural ones are ordered only partially. For example, there are no structure monomorphisms between two sets with the partitions:
are verified in an elementary way. However, unlike cardinal numbers, structural ones are ordered only partially. For example, there are no structure monomorphisms between two sets with the partitions: ![]() and
and ![]() (i.e., the corresponding structural numbers
(i.e., the corresponding structural numbers ![]() and
and ![]() are incomparable). Thus, functions defined on
are incomparable). Thus, functions defined on ![]() and taking values in
and taking values in ![]() cannot be used for formulating an extremum principle.
cannot be used for formulating an extremum principle.
Let us seek a way out of the above situation by constructing a suitable generalization of structural numbers. To this end, one should recall that S is a category and the factor class ![]() is ordered linearly.
is ordered linearly.
Given an arbitrary object A in the class ![]() , consider the mapping
, consider the mapping ![]() associating with each
associating with each ![]() the set
the set ![]() of structure morphisms from A to B and with each
of structure morphisms from A to B and with each ![]() the everywhere defined functional correspondence
the everywhere defined functional correspondence ![]() from
from ![]() to
to ![]() for any
for any ![]() . It is obvious that the conditions
. It is obvious that the conditions
are valid. Therefore, the mapping ![]() is a one-place covariant functor (Bucur & Deleanu, 1968) of the category S into the category Set. It is known as a representing functor.
is a one-place covariant functor (Bucur & Deleanu, 1968) of the category S into the category Set. It is known as a representing functor.
Following Levich (1982), we call the cardinal number ![]() the invariant of the object
the invariant of the object ![]() with respect to the object
with respect to the object ![]() . It is not difficult to prove the proposition:
. It is not difficult to prove the proposition:
if ![]() then
then ![]() .
.
Indeed, the inequality ![]() means that there exists a structure monomorphism of B into C. Let
means that there exists a structure monomorphism of B into C. Let ![]() be such a monomorphism and
be such a monomorphism and ![]() be arbitrary structure morphisms from A to B. Since b
is an everywhere defined functional injective correspondence, the equality
be arbitrary structure morphisms from A to B. Since b
is an everywhere defined functional injective correspondence, the equality ![]() implies
implies ![]() . Consequently,
. Consequently, ![]() is an injection of
is an injection of ![]() into
into ![]() and
and ![]() . Q.E.D.
. Q.E.D.
In particular, if ![]() , then
, then ![]() . This justifies the term “invariant” introduced above for
. This justifies the term “invariant” introduced above for ![]() . Since
. Since ![]() is a linearly ordered factor class, we have:
is a linearly ordered factor class, we have: ![]() or
or ![]() or
or ![]() for any
for any ![]() . Thus, one can compare objects of the category S by comparing their invariants. The last circumstance forms the basis of the functor method of comparison of structured sets (Levich, 1982).
. Thus, one can compare objects of the category S by comparing their invariants. The last circumstance forms the basis of the functor method of comparison of structured sets (Levich, 1982).
Having fixed ![]() , we obtain the function
, we obtain the function ![]() ,
, ![]() which is the composition of the injection
which is the composition of the injection ![]() ,
, ![]() and the canonical surjection
and the canonical surjection ![]() . The function
. The function ![]() is defined on the whole class
is defined on the whole class ![]() and takes values in the linearly ordered factor class
and takes values in the linearly ordered factor class ![]() , i.e., it can be employed perfectly well in an extremum principle.
, i.e., it can be employed perfectly well in an extremum principle.
Now, keeping in mind the subsequent applications to ecological communities, we concentrate attention on finite sets. Instead of S, consider the category ![]() whose objects are finite nonstructured sets and morphisms are correspondences between them having the type “a” (the multi-index a takes one of sixteen values which are subsets of the set
whose objects are finite nonstructured sets and morphisms are correspondences between them having the type “a” (the multi-index a takes one of sixteen values which are subsets of the set ![]() of the main types of correspondences listed in the previous section). Assume
of the main types of correspondences listed in the previous section). Assume ![]() ,
, ![]() , and
, and ![]() , where
, where ![]() are nonnegative integers. Let us denote by
are nonnegative integers. Let us denote by ![]() the invariant of the object
the invariant of the object ![]() with respect to the object
with respect to the object ![]() in the category
in the category ![]() . It is obvious that
. It is obvious that ![]() coincides with the number of morphisms from
coincides with the number of morphisms from ![]() to
to ![]() and is a function of m and n. The following is a list of the results of calculating the invariants for all the sixteen values of the multi-index a:
and is a function of m and n. The following is a list of the results of calculating the invariants for all the sixteen values of the multi-index a:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Here ![]() is the system of all coverings of the set
is the system of all coverings of the set ![]() ,
, ![]() , and
, and ![]() is an arbitrary k-element set.
is an arbitrary k-element set.
As a special case of S, consider the category ![]() such that the class
such that the class ![]() consists of finite uniformly structured sets and the class
consists of finite uniformly structured sets and the class ![]() consists of structure morphisms which have the type “a” as correspondences between sets (see the previous paragraph). The category
consists of structure morphisms which have the type “a” as correspondences between sets (see the previous paragraph). The category ![]() already gives sufficient possibilities for modeling a broad spectrum of natural systems.
already gives sufficient possibilities for modeling a broad spectrum of natural systems.
Let ![]() and
and ![]() be the invariant of the object B with respect to the object A in the category
be the invariant of the object B with respect to the object A in the category ![]() , i.e.,
, i.e., ![]() . (For example, if
. (For example, if ![]() is the category of finite sets with partitions, then
is the category of finite sets with partitions, then ![]() , where
, where ![]() is the i-th partition class of the set A and
is the i-th partition class of the set A and ![]() is the partition class of the set B into which the class
is the partition class of the set B into which the class ![]() passes as a result of morphisms from
passes as a result of morphisms from ![]() (Levich, 1982)). Moreover, let
(Levich, 1982)). Moreover, let ![]() be the same sets A and B, but only deprived of the mathematical structure on them (also known as supports of the structure). Consider the quantity
be the same sets A and B, but only deprived of the mathematical structure on them (also known as supports of the structure). Consider the quantity ![]() called the specific invariant of
called the specific invariant of ![]() with respect to
with respect to ![]() ; it has the meaning of the number of correspondences from
; it has the meaning of the number of correspondences from ![]() per one structure morphism from
per one structure morphism from ![]() . It is convenient to take the specific invariant as a quantitative measure of deviation of the structured sets A and B from the corresponding supports
. It is convenient to take the specific invariant as a quantitative measure of deviation of the structured sets A and B from the corresponding supports ![]() and
and ![]() of the mathematical structure. Applied to natural systems, this means that the states of a system with greater values of the specific invariant are “stronger” structured than the states with smaller ones.
of the mathematical structure. Applied to natural systems, this means that the states of a system with greater values of the specific invariant are “stronger” structured than the states with smaller ones.
According to the aforesaid, we introduce the following definition:
For a natural system admitting a description within the framework of the category ![]() , the logarithm
, the logarithm ![]() is called the entropy of the state
is called the entropy of the state ![]() with respect to the state
with respect to the state ![]() .
.
If a class of states between which transitions are permitted from the viewpoint of some substantial reasons, for example, due to conservation of macroscopic parameters of the system, is interpreted as a macrostate of the system and a result of an arbitrary transformation of the system is interpreted as its microstate, then ![]() is a generalization of Boltzmann’s entropy which is conventionally defined as the logarithm of the number of distinct microstates corresponding to a given macrostate. The possibility of the above interpretation and the coincidence of special cases of the quantity
is a generalization of Boltzmann’s entropy which is conventionally defined as the logarithm of the number of distinct microstates corresponding to a given macrostate. The possibility of the above interpretation and the coincidence of special cases of the quantity ![]() with the traditional formulae for Boltzmann’s entropy justify the term “entropy” applied to
with the traditional formulae for Boltzmann’s entropy justify the term “entropy” applied to ![]() . Note, however, that, in the present approach, the entropy appears without any probabilistic considerations.
. Note, however, that, in the present approach, the entropy appears without any probabilistic considerations.
For fixed ![]() , the entropy
, the entropy ![]() is a function of
is a function of ![]() taking values in the positive real semiaxis
taking values in the positive real semiaxis ![]() . Indeed, this follows from the obvious inequalities
. Indeed, this follows from the obvious inequalities ![]() and
and ![]() , where the supports
, where the supports ![]() of the structure correspond to the objects A, B and the variable
of the structure correspond to the objects A, B and the variable ![]() .
.
It is now clear that the desired extremum principle can be formulated in the form of the postulate:
In reality, a natural system passes from a given state ![]() to the state
to the state ![]() for which the entropy
for which the entropy ![]() is maximal within the bounds defined by the external conditions (for example, available power and other resources).
is maximal within the bounds defined by the external conditions (for example, available power and other resources).
The suggested principle admits the following interpretations:
In the next section we will discuss an ecological application of the above extremum principle.
THE EXTREMUM PRINCIPLE IN ECOLOGY OF COMMUNITIES
Consider an ecological community consisting of organisms of the same trophic level without an age structure (for example, cells of phytoplankton) which belong to w species and consume m mutually irreplaceable resources. Assume that in this community fission of cells and their death are admissible but absorption of one organism by another and introduction of organisms from outside are inadmissible. Since, in the adopted category-theoretic model of natural systems, states of the ecological community are described by means of sets with partitions, transitions between states of the community satisfying the above requirements are injective surjective structure morphisms of sets with partitions.
We will seek the stationary final state of the community. The following is a modification of the extremum principle for this special case:
In the course of time, the ecological community passes to the state ![]() with the maximum value of the entropy
with the maximum value of the entropy ![]() possible under the given resource restrictions.
possible under the given resource restrictions.
Let ![]() be the number of organisms of the species i in the community,
be the number of organisms of the species i in the community, ![]() be the vector of the species sizes,
be the vector of the species sizes, ![]() be the total number of organisms,
be the total number of organisms, ![]() be the amount of the k-th resource in the environment,
be the amount of the k-th resource in the environment, ![]() be the requirement of an organism of the species i for the k-th resource. Evidently, any admissible state of the community is characterized completely by the vector
be the requirement of an organism of the species i for the k-th resource. Evidently, any admissible state of the community is characterized completely by the vector![]() . One can show (Levich, 1982) that
. One can show (Levich, 1982) that ![]() where A corresponds to
where A corresponds to ![]() . On the other hand, we know from the previous section that
. On the other hand, we know from the previous section that ![]() . Thus, a conditional extremum problem appears (Levich, Alekseev, and Nikulin, 1994):
. Thus, a conditional extremum problem appears (Levich, Alekseev, and Nikulin, 1994):
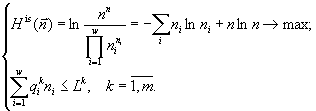
A solution of this problem is yielded by the species structure formula (Levich, 1980)
![]()
which connects the species sizes ![]() in the ecological community with the resources
in the ecological community with the resources ![]() on which n and
on which n and ![]() depend. Levich (1980) and Levich,. Zamolodchikov, and Rybakova (1993) have demonstrated the adequacy of the species structure formula to the empirical data (see also Lurie, Valls, and Vagensberg (1983)).
depend. Levich (1980) and Levich,. Zamolodchikov, and Rybakova (1993) have demonstrated the adequacy of the species structure formula to the empirical data (see also Lurie, Valls, and Vagensberg (1983)).
It has been shown as well that:
A solution of the extremum problem exists and is unique under any ![]() (
(![]() ) and realizes a maximum of the functional (the existence and uniqueness theorems) (Levich, Alekseev, and Nikulin, 1994).
) and realizes a maximum of the functional (the existence and uniqueness theorems) (Levich, Alekseev, and Nikulin, 1994).
The space of environmental resources consumed by the community splits (stratifies) into ![]() non-intersecting subsets, any of which corresponds to a unique collection of resources consumed completely; and in these subsets the state
non-intersecting subsets, any of which corresponds to a unique collection of resources consumed completely; and in these subsets the state ![]() of the community depends on the same resources as arguments and only on them (the stratification theorem) (Levich, Alekseev, and Nikulin, 1994).
of the community depends on the same resources as arguments and only on them (the stratification theorem) (Levich, Alekseev, and Nikulin, 1994).
The fractional sizes of the species depend only on the resource amount ratios in the environment and take the greatest values under the resource ratios which are equal to the given species' ratio of demands for them (the optimization theorem) (Levich, Alekseev, and Rybakova, 1993; Alexeyev & Levich, 1997). This optimization theorem creates an efficient method of management for the species structure of ecological communities with the aid of environmental resource factor flows (Levich & Bulgakov, 1993; Levich, Khudoyan, Bulgakov, and Artiukhova, 1992; Levich & Bulgakov, 1992; Levich, Maximov, and Bulgakov, 1997).
The variational problem of finding the maximum entropy under restricted (from above) environmental resource consumption turns out to be equivalent to the variational problem of finding the minimum environmental resource consumption by the community under restricted (from below) “structure entropy” of the community (“the Gibbs theorem”). This allows the suggested extremum principle to be interpreted as the principle of minimum environmental resource consumption (providing a sufficient degree of system organization) (Levich & Alexeyev, 1997).
REFERENCES
Alexeyev, V. L., and A. P. Levich. 1997. A search for maximum species abundances in ecological communities under conditional diversity optimization. Bull. Math. Biol. 59:649-677.
Baianu, J., and M. Marinescu. 1968. Organismic supercategories. I. Proposals for a general unitary theory of systems. Bull. Math. Biophys. 30:625-635.
Baianu, J. 1970. Organismic supercategories. II. On multistable systems. Bull. Math. Biophys. 32:539-561.
Bartholomay, A. F. 1960. Molecular set theory. A mathematical representation for chemical reaction mechanisms. Bull. Math. Biophys. 22:285-307.
Bartholomay, A. F. 1965. Molecular set theory. II. An aspect of biomathematical theory of sets. Bull. Math. Biophys. 27:235-251.
Bourbaki, N. 1960. Йlйments de Mathйmatique. Thйorie des ensembles. Paris: Hermann.
Bucur, I., and A. Deleanu. 1968. Introduction to the theory of categories and functors. London: John Wiley.
Goldblatt, R. 1979. Topoi. The categorial analysis of logic. Amsterdam: North-Holland Publ. Comp.
Leguizamon, C. A. 1975. Concept of energy in biological systems. A theory for environmental systems. Bull. Math. Biol. 37:565-572, 675-689.
Leguizamon, C. A. 1993. The periodic continuous effect in terms of the algebraic relational theory. J. Biol. Systems 1:1-25.
Levich, A. P. 1978. Information as system structure. Semiotika i Informatika 10:116-132 (in Russian).
Levich, A. P. 1980. The structure of ecological communities. Moscow: Moscow University Publ. (in Russian).
Levich, A. P. 1982. Sets theory, the language of category theory and their applications in theoretical biology. Moscow: Moscow University Publ. (in Russian).
Levich, A. P., E. D. Liubimova, and G. Sh. Martashvili. 1986. Species structure and the consumption of substrate and energy factors in laboratory algocoenosis. Ecological Forecasting, Moscow, pp. 69-103 (in Russian).
Levich, A. P., and N. G. Bulgakov. 1992. Regulation of species and size composition in phytoplankton communities in situ by N:P ratio. Russian Journal of Aquatic Ecology 2:149-159.
Levich, A. P., A. A. Khudoyan, N. G. Bulgakov, and V. A. Artiukhova. 1992. On the possibility of species and size community structure control in experiments with natural phytoplankton in vitro. Biologicheskiye Nauki 7:17-29 (in Russian).
Levich, A. P., V. L. Alekseev, and S. Yu. Rybakova. 1993. Optimization of the structure of ecological communities: model analysis. Biophyzics 38:903-911.
Levich, A. P., and N. G. Bulgakov. 1993. About the possibility of controlling of algal community structure in lab. Biology Bulletin of the Russian Academy of Sciences 20:457-464.
Levich, A.P., D. G. Zamolodchikov, and S. Yu. Rybakova. 1993. A study of the adequacy of a category-theoretic model of phytoplankton communities. Ecological Monitoring and Modeling Problems in Ecology 15:234-246 (in Russian).
Levich, A. P., V. L. Alekseev, and V. A. Nikulin. 1994. Mathematical aspects of variational modeling in ecology of communities. Matematicheskoye Modelirovanie 6:55-76 (in Russian).
Levich, A. P., and V. L. Alexeyev. 1997. The entropy extremal principle in the ecology of communities: results and discussion. Biophysics. 42:525-532.
Levich, A. P., V. N. Maximov, and N. G. Bulgakov. 1997. Theoretical and experimental ecology of phytoplankton: the structure and function of communities control. Moscow: SAL-Press (in Russian).
Lurie, D., J. Valls, and J. Vagensberg. 1983. Thermodynamic approach to biomass distribution in ecological systems. Bull. Math. Biol. 45:869-872.
Rashevsky, N. 1954. Topology and life. In search of general mathematical principles in biology and sociology. Bull. Math. Biophys. 16:317-348.
Rashevsky, N. 1955. The geometrization in biology. Bull. Math. Biophys. 17:31-56.
Rashevsky, N. 1955. Some remarks on topological biology. Bull. Math. Biophys. 17:207-218.
Rashevsky, N. 1955. Life, information theory and topology. Bull. Math. Biophys. 17:229-235.
Rosen, R. 1958. A relational theory of biological systems. Bull. Math. Biophys. 20:245-260.
Rosen, R. 1958. The representation of biological systems from the standpoint of the theory of categories. Bull. Math. Biophys. 20:317-342.
Rosen, R. 1959. A relational theory of biological systems, II. Bull. Math. Biophys. 21:109-127.