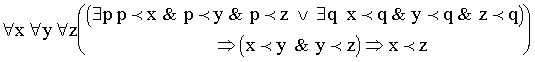In this paper about a hundred mathematical (geometric) terms connected with the collective and colloquial word "time" will be defined and described. However, those terms have not been thrusted from outside, as by an empirical generalization of the reality, or by its concrete realization within the system theory, or, say, by a system-theoretical specification of general philosophic categories.Those terms are thought of as a consistent development and complication of a single mathematical topic, namely, the order type relations. Those are relations which appear when the foundations of mathematics are developed, in mathematical logic and at the very outset of sets theory. Here we consider the "order" and its morphisms not in the most general form but in a specific modification allowing one to interpret the order in the form "one thing happened earlier than the other". Since the late sixties there has been a keyword for the studies in this direction, namely, kinematics (Pimenov 1968). Chronogeometry (Alexandrov 1959) deals with special problems of one of the kinematics, while related problems are considered within the "causal space-time structure" theory (Penrose 1968). We hope that our work will contribute to reducing the discord in the temporal terminology which sometimes makes mutual understanding at conferences rather difficult when representatives of different schools meet each other.

We will describe various mathematical constructions. Mathematics itself is to be understood here not as a teaching of numbers, quantities or in general something quantitative. It is to be treated as a certain LANGUAGE, the one forming only a very RESTRICTED part of a living human language, moreover, so much restricted that any MISUNDERSTANDINGS in using that language are EXCLUDED. Thus, mathematical logic allows one to use the words "and" (denoted "&"); "or" (denoted "Ъ "); "implies" ("Ю ") (in the context "the phrase A implies the phrase B", "the statement B logically inevitably follows from the statement A"); "is equivalent to" ("Ы "); "not" ("щ " or sometimes "~"); "exists" ("$ ") (so that the phrase "there exists an element x such that the statement P(x) is valid" is written in the language of mathematical logic in the form "$ x P(x)"); "for any" ("" ") (the statement "for any variable x with the variability domain X the assertion P(x) is valid" is written as "" xО X P(x)"); the phrase "the variable x for which P(x) is valid" is denoted "x P(x)", or sometimes "arg P(x) = 0". The notion "word", which is very complicated in socio-psychological, phonetic and semantic respects, in mathematical logic has the meaning of just a combination of letters belonging to a certain alphabet, or, more precisely, a sequence of letters. Instead, the numbers of right and left brackets are thoroughly counted.

Making the language poorer, one manages to work out some stable constructions, in whose respect it can be guaranteed that THEIR USE CANNOT LEAD TO A CONTRADICTION (i.e., to results like "0 = 1" or "A is not A"). This guarantee is twofold: on one hand, the theory of mathematical logic certifies that there will be no contradiction, and, on the other hand, the same is confirmed by employing these constructions in concrete computer programming. In that sense mathematics follows the precept of one of the founders of modern mathematics, Descartes, who said that any consideration should begin with the SIMPLEST item, with something clear and unambiguous, and only then gradually move to more and more complicated notions, preserving the clarity and reproducibility of thinking at each step. (This principle, like the others, was later mystified in the Hegelian school, where it was turned into the view that, supposedly, "nature" "develops from simplicity to complexity". Thus a feature of our cognition process was ascribed to the object of cognition.) In our presentation we would like to omit the proofs as a matter of technique, but only describe the results.

From the standpoint of mathematical logic any DEFINITION is not a reference to something known but just an ABBREVIATION of a few words or phrases to a single word. For instance, instead of saying repeatedly "the set A in a topological space cannot be represented by a union of two non-intersecting open sets" one says in short "the set A is connected". Instead of saying "an algorithm is given which works out for each natural number one of the figures 0, 1, 2, 3, 4, 5, 6, 7, 8, 9", one says "a constructive real number is given" and so forth.

A significant component in the usage of mathematical constructions is the INTERPRETATION operation. Its content is a juxtaposition of each mathematical symbol to something which does not belong to these symbols (Church 1956). Two types of interpretation are possible, namely, that WITHIN MATHEMATICS (also called formal), when a symbol is juxtaposed to another mathematical symbol belonging to another branch of mathematics. For example, the symbol "A < B" is juxtaposed to "the polynomial B is divisible by the polynomial A". Another type of interpretation, the so-called SUBSTANTIAL one, is more important. That is the operation when a mathematical symbol is juxtaposed to some entity OUTSIDE MATHEMATICS. For instance, the same symbol A < B is juxtaposed to the phrase "Ivanov is richer than Petrov". Or, for instance, the symbol {{Ж },{Ж , Ж }} (equivalently represented by the symbol "2") can be juxtaposed to "two apples", "two motor-cars", two different time instants, two reactants, etc. In such an interpretation its CONSISTENT and FORCED nature is of importance. That means that if we have once established such a correspondence, we must preserve it everywhere until our consideration is over, without hiding the cases when this correspondence, or identification, is unpleasant. ALL the symbolic relationships which have been derived mathematically, must be translated into the language of that interpretation. ALL the considered facts and objects must be represented in the language of the above symbols. It sometimes turns out that such an interpretation skids, stops being realizable. For instance, if we are considering a set of cities in a diachronic way and treating the above symbol as "two cities", then if two cities merge, a new object must be ascribed the symbol "{Ж }", or "1". However, that implies "2 = 1", i.e., a contradiction. Or, if we wanted to interpret that symbol as "two thoughts", we would immediately discover the iridescent, crumbling, universal character of a "thought", so that a number of thoughts could not be represented mathematically. The specific cases of the interpretation process will be followed below.

It should be pointed out that the manner of using the word "interpretation" is contrary in such areas as mathematics and archaeology. Thus, in sciences connected with mathematical logic and in neopositivism a transition from a verbal, "formal" model to "substantial" considerations, dealing with some objects which are given empirically, is called "interpretation". A reverse transition is called "explication". On the contrary, in archaeology interpretation is a transition from reviewing the survived pottery, logs, adornments, birch barks to verbally formulated models ("a historical fact", "culture", etc.), i.e., just the process called explication in physical and mathematical sciences.

We will adhere to the widespread naive set-theoretical language; a possible transition to various refined axiomatic set theories or to the modern language of category and topos would change essentially nothing in the models to be considered. Even a transition from the classical logic to a constructive, modal, temporal or quantum logic would hardly affect the foundations of the models to be considered here, although certainly the cumbersome constructions of our models must be dealt with in other ways in these logics.

Thus we are beginning with an object¹ called A SET. It is sufficient to know that such an object consists of ELEMENTS, or, technically, xО M, where x denotes an element, M is a set and the symbol О is read as "belongs to". An aggregate of elements a,b, ... from M itself forms a set denoted by {a, b, ...}. This is part of the set M, which is written as {a, b, ...} М M, where the symbol М is read as "is included in". A specific set which contains no elements is called an empty set and denoted by Ж . Thus we have introduced the following concepts: two objects, "a set" and "an element", two relations, "О " and "М " (both binary), a specific object, or, as it is sometimes called, "a constant", "an empty set", and the auxiliary symbol "{ }". These are all the starting concepts introduced. On their basis the following operations are constructed:

a) UNION of sets, when a summed set, A И B, is formed from the sets A and B;

c) COMPLEMENT of a set A to a set M, M \ A;

e) PRODUCT of sets M and N, Mґ N, i.e., the set of pairs

Mґ N={(x,y)Ѕ xО M & yО N};

f) THE SET N^M OF MAPPINGS (functons) from M to N, i. e.,

N^M={fЅ f: M ® N}.

Usually instead of щ xО M it is written xП M, etc.

We are presenting these operations just as a reminder (see Levich 1982).

The formal concept of a set consisting of elements can be interpreted as, e.g., the set of pages of this book, the set of all grains of sand in a given pile, the set of all stars, of all the God's angels, etc. It cannot be interpreted as the set of all the drops in the ocean, since the drops cannot be separated from one another, or the set of all elementary particles due to their mutual transformations, i.e., the absence of a stable state.

In addition to the concept of a set, we will assume that the concept of a real number is known; the set of all the standard real numbers is denoted by R. As soon as these objects are given, we can construct derivative objects from them, such as a mapping f: A ® B of the set A into the set B, or a mapping g: C ® R from a set C into the set of real numbers. (Formally the first is a certain subset f М Aґ B, where Aґ B is a "product" of a pair of sets; however, we will not be concerned with such refinements.

The whole consideration of ours will be carried out in three levels. THE FIRST LEVEL assumes that we have nothing and as though know nothing but AN ABSTRACT SET M and the set of REAL NUMBERS R. This level of consideration will be called the set-theoretical level (sometimes also "topological" as long as such a familiarity of speech is justified).

At the SECOND LEVEL we assume as given, in addition to M and, also a TOPOLOGY, i.e., a certain T М 2^M, and SMOOTHNESS, a certain F М R^M. At this level such terms appear as "a differentiable manifold", "a tangent space", "a covariant derivative", etc. We will call this level "differential-topological", or "differential-geometric". General relativity corresponds to this level of consideration.

At the THIRD LEVEL we assume that two additional OPERATIONS are given: "+": Mґ M ® M, and "Ќ ": Rґ M ® M. Thus we obtain the so-called "linear structure" (also called the "vector", or "affine" structure). This third level contains, for instance, Euclidean geometry and special relativity.

Order type relations will be present in our consideration at all the three levels as basic ones. Such a relation connects two elements x and y from a set M, therefore it is "binary", or "two-sided". Three sorts of such relations will appear: "<", the STRICT ORDER relation, " Ј ", the PRE-ORDER relation, and "p ", the LOCAL SEQUENCE relation.

The first one is antisymmetric (щ x < y & y < x)

and therefore unreflexive (щ x < x). It is transitive (x < y & y < z Ю x < z). The second one is reflexive and transitive, while the number of elements for which x Ј y & y Ј x is valid, varies from x = y to richer sets. The local sequence relation is antisymmetric but satisfies only the LOCAL TRANSITIVITY axiom:

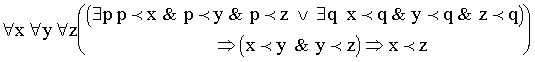.(2.1.1)

Local sequence can also be introduced in another way, by combining the strict order relation with the proximity relation a к b (a version of the tolerance relation) but here we would not like to be absorbed in these subtleties (Pimenov 1970, 1987). Let us instead give some examples (interpretations inside mathematics) of order type relations. Clearly "<" is a particular case of "p ".

EXAMPLE 2.1.1. The order of real numbers is well-known, such as 1 < 2, 3 < < 8 < 2 and so forth. It is a strict order.

EXAMPLE 2.1.2. The inclusion relation for sets, "М ", satisfies the pre-order axioms if considered in 2^M . Indeed, if A, B, C М M and A М B, B М C, then one can assure element by element that A М C. In this case A М B & B М A Ю A = B, therefore the relation М is sometimes called "unstrict order" instead of "pre-order". It should be noted that the relation О is not transitive (since xО {x} but xП {{x}}) and hence is not an order type relation.

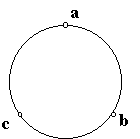
Fig. 1.

EXAMPLE 2.1.3. Let us introduce a direction (orientation) on a circle, for instance, clockwise (Fig.1). Let us say that x p y if, in the sense of the orientation, x precedes y and the angular distance between x and y is less than 180° . Then for the points x, y and z separated by angles of 120° , it is true that x p y & y p z & zp x but it is wrong that x p z. However, a local sequence relation must not necessarily contain such closed cycles.

EXAMPLE 2.1.4. Let x, yО R. Let us say that x p y if x < y as ordinary real numbers and, in addition,│ x-y│ < 10. In this case 1p 9p 15 but it is wrong that 1p 15 (as well as that 15 p 1).

Taking Example 2.1.3 with angle smaller than 180° , one can vary the relation p in such a way that the chain ap bp cp a would be impossible while the chain ap bp cp dp a would remain possible, and so on.

EXAMPLE 2.1.5. In a non-mathematical context the relation < can be interpreted as a "preference relation" in economy: x < y means that a customer prefers the article x as compared to the article y.

EXAMPLE 2.1.6. In the same spirit one can interpret the relation x p y as the fact that usually Ivanov (x) loses chess games to Petrov (y). It can also happen that normally Petrov loses to Sidorov while Sidorov in turn loses to Ivanov (a closed chain).

Unlike Examples 2.1.1-2.1.4, the last two do not require quantitative criteria.

For a theory of space-time the following two examples within mathematics are of extreme importance.

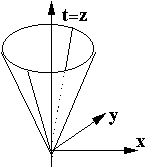
Fig. 2.

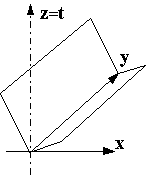
Fig. 3.

EXAMPLE 2.1.7. Let us consider the right circular cone with the vertex (0,0,0) in the three-dimensional Euclidean space. Let us imagine a similar cone at each point. The relation Ј introduced by the formula

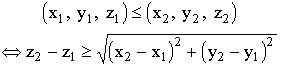
is an unstrict order relation. Figure 2 expresses this order by the fact that the point (x₂, y₂, z₂) is INSIDE OR AT THE BOUNDARY OF A CONE with the vertex at the point (x₁, y₁, z₁ ); in particular, the points (x₁, y₁, z₁ ) and (x₂, y₂, z₂ ) may coincide.

EXAMPLE 2.1.8. An order relation in the same space can be defined using a dihedral angle instead of a cone (Fig.3). The definition is given as follows

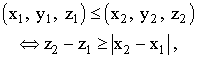
which does not contain the y coordinate! This time it is a pre-order relation: if

,

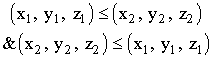then the second point lies at the edge of our dihedral angle x = x₁, z = z₁, i.e., it is an arbitrary point on the y-axis.

These are, in principle, all the simple examples of order type relations. Unfortunately, only the first one is widely known. For simplicity here we will not be concerned with the cases when several sets are given, each with its own order type relation, with a certain matching of orders at set intersections. Such a LOCAL DEFINITION of order should not be confused with a LOCAL SEQUENCE which is nevertheless a SINGLE one in the WHOLE set and in that meaning is "global".

A specific interpretation for considerations involving "time" is the one where a < b is understood as "a is earlier than b". The very word "time" is understood "collectively", like a label on a chest where various terms and combinations of terms denoted by this label in their totality are collected. A standard interpretation of a point from a set is that of an "instant", "an instantaneous event", "something that has neither length, nor width, nor height, nor duration"; at any rate, the context of usage contains the word "duration" in that or other way. Thus the symbolic formula a < b can be read more exactly as: "the event a has happened, or is happening, or will happen² earlier than the event b".

EXAMPLE 2.2.1. An actual repeat of Example 2.1.1: we associate each real number with a certain date, or temporal characteristic (temporate) of an event X. The entry x < y means that X (the event having the temporate x) happened EARLIER THAN the event Y with the temporate y. This is a way to describe the temporal model where "time flows" between -Ґ and +Ґ in a continuous way, passing through all the real number values. This is a strict order with no first or last element (neither world creation, nor end).

Clearly there is a conceptual connection between the chronological idea "earlier - later" and the causal idea "because". "Propter hoc ergo post hoc" is commonly adopted without doubt, the opposite being ridiculed. Sometimes these ideas are somewhat identified: if a is earlier than b, then the physical (or psychic) process in a could somehow affect something that happened in b, therefore one can treat a in a certain sense as a cause of b - that is how some authors reason. Such an understanding of the relation < as a POTENTIAL CAUSE is very fruitful in some studies. However, firstly, this terminology makes no difference between "a factor" and "a cause" and, secondly, the transitivity of < can lead to a blind alley. Something like that: my parents got acquainted BECAUSE my father wore a cap. Later I was born and eventually graduated from the university. Can I say, by transitivity, without looking like Kozma Prutkov, that I graduated from the university BECAUSE my father had worn a cap? To avoid such nonsense it is better to use the local sequence model. The events which are too remote in time can be considered to be connected neither causally, nor chronologically; however, the word "remote" is to be understood only qualitatively, not quantitatively.

Examples 2.1.3 and 2.1.4 are interpreted in a similar way. The words "due to", "despite", "because of", "regardless of", "cause", "consequence", "factor", "effect" and others acquire the character of local, close links when a local sequence is used. Thus cycles like a₁ p a₂ p a₃ p ... a_n p a₁ become possible and can be interpreted either as a time machine, or as "I.A.Arshavsky's metabolic cycle".

EXAMPLE 2.2.2. This example is a temporal re-formulation of Example 2.1.7: the coordinate z is replaced by the "temporate" t and, for physical clearness, the constant c called the velocity of light is introduced. The formula takes the form

(2.2.1)

and means: the event (t₂, x₂, y₂) chronologically follows the event (t₁, x₁, y₁) if (t₂, x₂, y₂) can be reached by moving from (t₁, x₁, y₁) at a velocity less than or equal to c. This chronological ordering forms the basis of special relativity, while its certain generalization in a similar way underlies the so-called chronogeometry (Guts 1982).

EXAMPLE 2.2.3. Example 2.1.8 is re-formulated in the same way, replacing z by t. Now the formula

(2.2.2)

means that motions in the abscissa direction have a finite maximum velocity (the unit one in the scale adopted), while in the y direction motions with any velocities are possible: -Ґ < dy/dt < Ґ . Such a model applied just to SPACE is hardly convenient, but applied to quantities of different dimensionalities (physical, biological or other), this idea does not look very ugly. For example, if e is a charge, no restrictions are known in physics upon the quantity de/dt, therefore, replacing y by e, one obtains a multidimensional unified model of space-time-electricity with no contrast to the experiment.

In the following the object of our consideration will always be a structure of a "partially ordered" set (M, <) (where M can vary) where < (or Ј , or p ) is interpreted as "earlier".

To shorten the formulations we need one more derivative concept.

DEFINITION 2.2.1. The set {xп a p x p b}=(a,b) is called an INTERVAL with vertices a and b (where either a < b, or a Ј b, or a p b).

Let us recall that there is a widespread word usage connecting the word "interval" with a NUMBER, a numerical measure of the distance between a and b. Unlike that, we call an interval a set of the same nature as the beginning (a) and the end (b) of an interval. In a given partially ordered set M the intervals are selected as a certain class of subsets, in other words, they define a TOPOLOGY. Therefore, dealing with a partially ordered set, we actually deal with a certain topological space. We will use this fact in what follows, allowing ourselves to speak of connection, continuity, the boundary ¶ A of a set A М M, etc., in the sense of just that interval topology.

Let us point out two concepts of interest for interpretation:

DEFINITION 2.2.2. The set {xЅ a p x}, denoted by a+, is called the FUTURE of the event a. The set {xЅ x p a}, denoted by a- , is called the PAST of the event a.

If at the outset we had a strict order or a pre-order, then (a,b)=a+З b-. For a local sequence it is not the case.

There is a specific case of ordered sets of particular interest, namely, LINEARLY ORDERED sets. This is the name of the structure (L,<) (we are using the standard notation L instead of M corresponding to an arbitrary set) for which the following axiom is valid: " x,yО Lx < yЪ x=yЪ y < x. For the relation Ј the same formula is valid, while for p the quantifier " x,yО L is replaced by " a,bО L " x,yО (a,b).

All the linearly ordered structures split into two homotopic types: a linearly ordered set can either be "infinite", or "linear", i.e., there are no chains like a₁ p a₂ p ...p p a_n p a₁ or "closed", "cyclic", containing such a chain with n > 2, so that for each xО L there exists a number i = 1,..,n such that x p a_i, or x = a_i, or a_i p x.

These two types can in turn be divided into subtypes depending on whether or not between any two given a and b (a < b) one can always find an event (an element, a point) x such that a < x < b (the QUESTION OF SPLITTING). In this way the so-called "discrete" (or "e-unconnected", as they are sometimes called) models are selected. An extreme case here is that of sets M with finite number of elements, so that the theory of partially ordered sets becomes finite graph theory. We do not consider this case. Such graphs are used in cybernetics and evolution theory. However, the models most widespread in physics and everyday life are those in which between any a < b as many points can be inserted as one wishes. For such models the following topological question is significant: is the interval (a,b) connected for arbitrary a,bО L ? Historically, this question was first formulated in the form of Dedekind's continuity axiom. Pursuing the study of possibilities (are there infinitesimal quantities? Are there ordinals or not?), we finally arrive at the two basic models: either the one from Example 2.2.1, with the infinite set R of real numbers , or

EXAMPLE 2.3.1. L is the set of all real numbers modulo 1. The relation б is defined for those pairs of numbers for which x < y and y-x< 1/2 (mod 1).

In both Examples 2.1.1 and 2.3.1 the number values as such are insignificant: in the first case everything is considered up to ordered homeomorphisms (that is, transformations f: Ra R under the only requirement x < y Ы f(x) < f(y)), while in the second case up to oriented homeomorphisms.

One can speak of homeomorphisms here because the interval topology for a linearly ordered set is very good (separable) and all the topological constructions become applicable.

The linearly ordered model is interpreted in a substantial way as a "temporal flow", "time by itself". We have nothing outside that would be dated by that time (i.e., nothing but the set L). We imagine just a set of events with a prescribed transition (orientation) from earlier to later ones, and that is all. According to Bergson, time is a pure duration, just as it is modelled by the linearly ordered model. Psychologically we can move either passing to later and later events each time NEW ones, or passing to those which have EVER HAPPENED, all that is just a secondary detail compared with the linear process of imaginary motion, without moving aside, branching or interruption. It is important that the pure, continuous (technically, "connected") duration, deprived of a spatial extent, is explicated by a linearly ordered structure. A conceivable transition from an earlier event (or events) to a later one (ones), sometimes described by the inaccurate and superfluous phrase "transition from the past to the future", is a purely speculative transition IN THE FRAMES OF THIS CONCEPTUAL STRUCTURE. (Let us note that within a cyclic structure the past, the present and the future DO NOT exhaust the whole linearly ordered cycle: " a a^- И a И a⁺ № L.) When this speculative transition is mystified as something taking place "in nature", "in reality", "independently of the cognizing subject", it leads to hypostating (substantification) of the "time flow". This explains why I called such time in some of my papers "substantial time", meaning that "substance" = "set". However, even when such a name has been given, there remains the relational character of the notion of time, i.e., it is based on an order type RELATION. It is impossible to formulate something in the above definition for (L, <) without that relation.

Substantial time is something self-contained, in no way connected with "external events". Modelling these events by some other set U and calling it "a universal", we will present another construction, a more complicated one. It can be interpreted as a temporal characteristic as well, but already for a universal. Starting from the already adopted idea of connecting the label "time" with the "earlier - later" relation, we would like to assume that a certain order type relation (<, Ј , or p ) is defined in the universal U; let us denote that relation by . If we dealt with a set U UNEQUIPPED with an order type relation, we could hardly use the terminology connected with time.

DEFINITION 2.4.1. We shall say that the mapping f: (U,)® (L,p ) is the FUNCTIONAL TIME if (L, p ) is a linearly ordered set and from xy it follows that f(x) p f(y) " x,yО U.

Technically speaking, f is an INCREASING (isotonic) function, or in other words, AN ORDERED STRUCTURE MORPHISM. Actually this means that we identify our speculative direction of running over events (L,p ) with the time describing the events external with respect to us, in some alien universal (physical, biological, geological) if and only if the earlier events, with respect to the order defined there, are earlier in our ordering (L,p ) too.

Here the specific case (the most widespread one) is possible, when L itself is viewed to be contained in the universal U, so that the orderings coincide:. Then the following formula is valid:

" x,yО Ux p y Ю f(x) p f(y). (2.4.1)

The above definition includes the arrow ® , not a . This is not an accidental error. We mean a mapping from U to L. The definition domain dom f of the mapping f can be different from the whole universal U, i.e., the case dom f U is admitted. Similarly sometimes the image f(U) L.

In what follows, when speaking of functional time, we will always write, instead of the arbitrarily taken letter f, the letter t. The case t(U) № L means that we have chosen the time L redundant for describing the given universal. For instance, L is defined as the whole number axis R, while all the considered psychic processes last not longer than a hundred years. The example of modern physical cosmology is the brightest: it uses the time defined on the axis (-Ґ , Ґ ), while all its models are confined to the semiaxis (0, Ґ ) and the zero point does not enter any physical model without a singularity. The difference between t(U) = L and t(U) № L is of particular significance in the case when a closed set (L,p ) is taken. Then t(U) № L means that we have chosen a closed (L,p ) in vain, since the universal under consideration CAN be described in terms of a linear time. The equality t(U) = L means that we have chosen the time without redundancy.

It is worse when dom t № U. This means that L is NOT A GLOBAL TIME for the given universal. There are events uncovered by our time t, i.e., events xО U without a temporate t(x)О L. Certainly such a thing can happen due to an unlucky choice of the mapping and each event will have a temporate if we take another time. However, it can happen (and such examples are known) that (U,p ) is such that one CANNOT choose L ® U and t: Ua L in a way preserving the global order. That means that universals are possible which do not admit a global ("unified") time. In the sense of cognition, that implies that it is forbidden to speak of entropy in such universals, since entropy is a function increasing with time, and if time itself cannot be defined, one cannot speak about functions of it.

Thus when we are speaking of time, we are PROJECTING the whole world diversity, with its spatial, gravitational, electric, metabolic, soil, genetic, chemical, psychic, ethic and magic characteristics ONTO ONE LINEARLY ORDERED AXIS. Such projecting is not necessarily connected with time, for instance, "thickness" can be projected to the abscissa axis. Only if projecting conserves the relation "earlier", it has something in common with the word "time".

At the second, differential-topological level of study the functional time t becomes a function whose gradient is positive (directed to the future in the tangent space).

Having at our disposal the time (L,p ) in a universal U, we can put "dates" into correspondence to events xО U in two ways: as INSTANTANEOUS DATES (temporates) and as TOPOLOGICAL DATES (intervals).

DEFINITION 2.5.1. The TEMPORATE tx of an event xО U in the temporal flow (L,p ) with respect to the functional time is the value of t at x, i.e., t_x = t(x).

Just the temporates are most commonly used, so that L is identified with R (we will take up the latter identification later on). A temporate, in particular, a numerical one, is very convenient to deal with. However, one should keep in mind that the function t is very arbitrary, it can be replaced by another function with the same isotony property but with other values. In particular, for the same pair of events it can turn out that t_x = t_y but .

DEFINITION 2.5.2. We will call the events x,yО U SIMULTANEOUS with respect to the functional time t if .

Thus the same pair of events can be simultaneous or not with respect to different functional times. There emerges a desire to find a UNIQUE function T which could be selected among all the other possible increasing functions tО L^U by some acceptable properties. Only that function is to be taken for THE TRUE TIME in the universal, while the others are to be discarded as figments. An alternative direction of thought is to accept ALL (or almost all) the admissible tО L^U on equal terms and thus not to ascribe any consistent meaning to the equality of temporates, t(x) = t(y): this equality is not invariant and therefore has no cognitive meaning. In special relativity the second viewpoint is dominating, while in Newtonian physics and in modern physical cosmology the first one is. Mathematically the result depends on the initial way of ordering in the universal; there is such an ordering method (called NEWTONIAN ORDERING) that the desired function T exists and is determined unambiguously in a certain sense (see Sections 3.1 and 3.2).

DEFINITION 2.5.3. We define the INTERVAL DATE (a,b)_x of an event xО U in the temporal flow (L,p ) as

(a, b)_x = L З (p, q)

p,qО L & xО (p,q) . (2.5.1)

Let us unravel the content of the definition. Let xО U be an arbitrary event. Let us find in L a pair of events p, q "dating" the event x in the following way: xО (p,q). This is a rough dating, indicating only that x is later than p but earlier than q. By the way, it can happen that even such a dating is impossible, i.e., (a,b)_x = Ж . However, if the above events p and q have been found, then the interval of the temporal flow LЗ (p,q) can be made more accurate, i.e., smaller. Namely, inside it one can find such p' and q' that xО (p', q') is again valid. When we continue this process boundlessly, we shall find either that the limit (intersection) of all such intervals is a unique event a, so that (a,b)_x = a, or the limit coincides with an interval (a,b)З L of the temporal flow (L,p ), so that (a,b)_x =LЗ (a,b).

The case when (a,b)_x = Ж corresponds to the absence of a global time. The case when for any event xО U the interval date is reduced to a single point, is precisely the situation which we have called "the Newtonian ordering of the universal". Finally, the case of a "dilute" date corresponds to the difficulties emerging in studies of temporal phenomena due to relativity theory. In the cognitive aspect the most significant in the "interval data" concept is the fact that in many widely accepted models having the label time" an event can be dated in an invariant way only if it is SMEARED OUT along a whole interval. According to Definition 2.5.3, no functional time is present in an interval date, i.e., the interval (a,b)_x is invariant with respect to the choice of tО L^U (but not L М U). The invariance is to be paid for by smearing-out. It should be taken into account that ONLY those phenomena (events) are smeared out which occur OUTSIDE the temporal flow itself (xО U \ L); therefore, for instance, the smearing-out³ does not apply to the experiments of A.A.Kronik and E.I.Golovakha (Golovakha and Kronik 1984) which have been implemented in the psychic time of the test subject. It is also significant that all the dating smearing-out models are somewhat connected with the short-range interaction idea.

A criterion for the possibility to choose L М U as a global temporal flow admitting an interval dating of the universal, (U, p ), is

U М И {x| ap xp b & ap b & a,bО L}. (2.5.2)

A linearly ordered (L,p ) can be associated with numbers, generally through a mapping t: (L,p )® (R,<) (certainly with order preservation) but most commonly by a direct identification of L with R and their orders. Evidently there is no "unique true" way to put into correspondence events and numbers. Each juxtaposition of this sort,

(2.6.1)

is called a CLOCK if xp y Ю t° t(x) < t° t(y).

The greatest convenience of the Newtonian ordering is that it allows one to be restricted to only ONE single clock (compare Section 3.3). Technically speaking, this circumstance is connected with the fact that the binary relation "the events x and y have the same interval date coinciding with a single point" is an equivalence relation in conformity with the pre-defined order of the universal. A factorization with respect to this equivalence - simultaneity relation leads to a linearly ordered set, i.e., to (L,p ) in (2.6.1).

At the second level of study (with the same Newtonian ordering) all the simultaneous points form a layer, a hypersurface where the metric is degenerate, so one has to introduce, instead of Riemannian or pseudo-Riemannian geometry, a semi-Riemannian (or, accordingly, semi-Euclidean at the third level of study) geometry.

DEFINITION 2.6.1. If the Newtonian ordering is valid, a TIME INTERVAL between the events p and q from a universal U with respect to a clock t is the number t(q) - t(p).

If two clocks, t: L® R and : L® R , are given in a linearly ordered L, one can speak of clock regraduation : t° ^-1: R® R ; this function will always be increasing, too.

Most probably, the first to meditate deeply on the regraduation problem was Poincarй, although he preferred to discuss the problem in terms of space rather than time. Most clearly the problem was formulated and in a certain way solved by Milne. Though, he set it up in the standard mystified form.

He posed the question: which time scale is CORRECT, the one in which equal FRACTIONS of a radioactive substance decay in equal time intervals, or the one in which equal MASSES of the same substance decay in equal time intervals? If we denote the times in the two scales by t and t, then, since in the first scale the mass decays exponentially, the times are connected by t = t₀log(t/t₀) where t₀ and t₀ are dimensional constants. Which of the two scales is "correct"? Mathematically, the point is not "which of the scales is more correct" but the possibility to identify that or other scale in some way, i.e., their invariant properties, if any. Milne considered the physical consequences of a transition from one scale to another; it will be more appropriate for us to deal with it in detail in one of the subsequent sections (see Section 3.2). A similar logarithmic transition was used in the same decades by Backman in his bioecological studies.

It should be noted that a transition to another scale through a logarithm is monstrous from the cognitive viewpoint. It changes the QUALITATIVE picture. Something that looked FINITE (the interval from 0 to t₁ ) becomes INFINITE (the beam from - 8 to t₁). Concerning stereotype breaking, such a transition just corresponds to the one proposed by Milne for radioactive decay measuring: to measure time not by the decayed matter fraction but by grams of it.

Another example of this sort of difficulty in passing from infinite to finite quantities in physics is connected with black holes: a particle of matter which falls freely to a black hole, reaches it in a FINITE time interval as measured by its own clock, while by the clock of any observer who is not falling to the black hole (and from the standpoint of the world time defined for this Schwarzschild solution) the particle will fall an INFINITELY LONG time. Therefore it is not clear how can the physical laws be the same for those who experiences so different time intervals between the same events.

There exist regraduations of less drastic nature, for instance, in relativistic cosmology it is natural (see Section 3.1) to use a transition by the formula

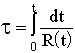, (2.6.2)

where R(t) is a well-known function in cosmology. In most of the models R is such that finite intervals are converted into other finite ones (i.e., the integral converges at zero) and no infinities appear. However, such reparametrizations cause cosmological scale changes so strong that the content of physical cosmology acquire absolutely other features.

In Newtonian physics clock regraduation was dealt with (before Poincarй) in the following way. Yes, in kinematics any transformation from one sort of temporates to another one, t ® t' (more precisely, R ® R) is quite legal and there is no reason to prefer any selected graduation. However, already in dynamics it is evident that the form of the equation is changed by a regraduation: dmv/dt = Fdt/dt, i.e., an undesired coefficient before the force appears. Hence, the DYNAMIC TIME is selected unambiguously (up to a scale factor and an additive constant). But Poincarй's conventionalism finds an objection: why don't we admit that the forces are graduated incorrectly, that the coefficient dt/dt is just a correction for the force? In the course of physical view evolution in the 20th century this objection was put aside but so far it remains unanswered. Another way of regraduation removal is pointed out in Section 3.3.

An operation in a certain sense reverse with respect to projecting a whole universal U upon a linearly ordered time L, is injecting this linearly ordered time L into a universal U.

DEFINITION 2.7.1. Given a linearly ordered time (L,p ) and a universal U, an isotonic mapping g: L a U is called a POINT OBSERVER L in U. In particular, a clock R can be taken for L; L itself is the image of L in the mapping: L = g(L) М U.

In literature the mapping g: [0,1] a (U,p ) is given different names: "a material point", "the world line of a material point", "an observer's world line", "an isotonic curve", "an isotonic path". At the differential-topological level of consideration there appear such terms as "a timelike curve", "a curve with a positive tangent vector" and even "a timelike geodesic". At the third level the most common terms are "an inertial particle" and "a timelike straight line". Creating a rigorous formulation of all the definitions, one has to recall the regraduation problem and take into account the difference between "a path" and "a curve" (the factor sets of the sets of all paths with respect to an isotonic regraduation, or reparametrization).

Essentially that means that a carrier of a self-contained time, or of a pure duration, in his mental act transfers that duration to the descriptions of all the phenomena and processes outside himself. Thus, living here, on the Earth, I assume that at Syrius (simplified to a point volume and accordingly deprived of structure) the proper time behaves in the same way as here (speaking of the direction and continuity, not of clock rate and graduation, discussed in Section 2.8). The phrase "There exists a material point (point particle)" now means that something connected with that point, has a DURATION, and for each change of the duration (creation or annihilation) with respect to mine, (L,p ), certain concrete explanations and reasons are required. Of course one can consider not a single observer but a system of observers.

DEFINITION 2.7.2. A FRAME OF REFERENCE W in a universal (U,p ) with a linearly ordered time (L,p ) is such a set W of point observers in this universal and with this time for which:

In the language of geometry such a family of curves is sometimes called "a congruence". At the second, differential-geometric level of study this definition of a frame of reference acquires the following form: "A frame of reference is a nondegenerate timelike vector field in a domain". In addition, such terms as "matter flows", "streams", "flows of material particles" are sometimes used. At the third level a frame of reference is most frequently reduced to a field of parallel straight lines. In this case it is redundant to speak of a "field", or a "congruence" because the whole frame of reference is given unambiguously by a single straight line. Therefore in this case it is usually pronounced, instead of the words "the frame of reference W ", "the observer g ", meaning gО W . However, even at the third level other frames of reference can also exist and we shall soon discuss them in more detail.

Without fixing ourselves at the questions connected with reparametrizations of the frames of reference and also with matching the mappings R , let us take up the difference between a "frame of reference" and "a coordinate frame", since these notions are often confused. At the second level, where, instead of sets, one can speak of smooth manifolds, each event is juxtaposed to the coordinates x=(x¹,..., xⁿ) in a certain map. Mathematically the maps are quite arbitrary, and in a transition to another coordinate frame the transformations between the old and new coordinates are quite arbitrary:

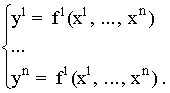(2.7.1)

only the functions f¹, ..., fn must be differentiable.

Frames of reference are another thing. For them, irrespective of the coordinate arbitrariness, a congruence of curves is chosen to play the role of temporal coordinate lines. A factorization with respect to this layer leads to the (n-1)-dimensional base of the fiber bundle, so that now the allowed coordinate transformations are of the form

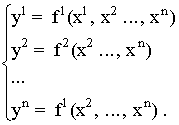(2.7.2)

Let us point out in passing that for the case of Newtonian ordering, when there is an (n-1)-dimensional layer of simultaneous events while the base of the fiber bundle is one-dimensional, the allowed coordinate transformations are

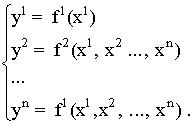(2.7.3)

At the differential-geometric level both cases (2.7.2) and (2.7.3) can be described in terms of the so-called semi-Riemannian geometry (Riemannian geometry with a metric tensor degenerate on a layer - this is the way it can be approximately sketched), and , respectively (Pimenov 1968).

It is sometimes in the case of mechanics, and the more so in biology and psychology, more reasonable to consider an object to be structured, complex rather than point-like. In such cases it is often also useful to apply a linear (chronological) time referred to something like "the center of mass". However, such an object can yield other quantities having the dimensionality of time (for instance, a pendulum clock with a "wrongly" suspended pendulum, or metabolic reaction rates, like growth of a man's beard). Let A be a symbolic (operator) description of our object, a a certain parameter set and f a certain function of all these parameters and the chronological time t. Then in general

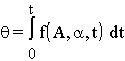(2.8.1)

is a time transformation sometimes interpreted as a transition to the proper, "biological" time of the biological object A under the conditions a. This approach makes it possible to remove a contradiction sometimes ascribed to the difference between the "biological" and "physical" times: the "biological time" is now just the chronological time (sometimes identified with the physical one) transformed under the influence of the organism A. Such A-transformations can refer not only to biological but also to some physical objects. Thus, sometimes physiological time is measured by the amount of physiological processes occurred and it is said that, for instance, "the time when someone is asleep is passing in another way than when he is awake". From the A-transformation viewpoint such a manner of expression is similar to the following: let us measure time for a kettle by the boiled water volume, then observations of how that volume depends on the voltage applied to the electric oven enable one to say that the kettle's time has different rates at voltages of 200 V and 230 V.

These A-transformations are carried out solely along the world line of the object A: only here t ® q , while in the surrounding universal nothing is affected.

In principle, the operator A can possess such properties that for some positive t negative values of q are yielded. Such an interpretation applies to Golovakha and Kronik's (1984) experiments with "calendar sheets mixing" if one interprets A as "a forgetting operator", "an inattentiveness operator", or "an inadequate wording operator".

The operator A allows one to interpret E.E.Selkov's experiments if one considers q to be a certain indicator of chemical reactant concentration; in this case it is of importance that the transformation t® q , is reversible, i.e., a single-valued function t(q ) exists and that is why those metabolic reactions can play the role of "a biological clock". The operator A can also yield periodic A-transformations, which are sometimes characterized by the words "a cycle", "a rhythm" (Rhythms of space and time, 1974) and even treated as examples of "closed time". The latter is hardly plausible. For example, if q is measured by the pH scale, a clearly expressed example of such cycles, or periods, is the acidity in a vagina: from high acidity to a neutral condition and a subsequent alkalinity increase, then an ovulation and a new period begins. However, the organism keeps in memory all the preceding periods, so that there is no ground for replacing the linear time by a periodic one.

The A-transformations are a specific case of clock regraduation; however, there the transformations were entirely arbitrary, while here we are dealing with .

Such a dependence of a regraduation on a specific operator A creates quite a new attitude to regraduations: in the former case it was a spontaneous noise, you did not know how to get rid of it, while in the latter it looks like an "objective" result of the object's influence to be studied with a hope to gain an insight.

It is natural to call "physiological process rate of an object A with respect to the chronological time". It should always be remembered that a "rate" is a two-sided (sometimes three-sided) predicate and the expressions like "a rate" and "something's rate" are incomplete.

To conclude the section, let us make a remark, not referring to it directly but often forgotten due to its triviality and creating wrong directions of thinking.

In some spaces of properties (mostly in physical spaces) the equation Ax = lx is valid. That means that l is an "eigennumber" of the operator A. It is very easy to arrange the constant l to have the dimensionality of time: for instance, if l is a wavelength, it is sufficient to divide it by the velocity of light. The relation of these "eigenvalues of time" to the problem of time is external, inessential by nature, although such eigenvalues can be very convenient for system descriptions.

The very problem of defining simultaneity appears to be difficult if we abandon considering time as something self-contained and start discussing a universal possessing some properties other than temporal (the space-time properties in physics, taxonomical, serological or other properties in biology, see Section 3.5). However, if the ordering is Newtonian, there is no difficulty: each event x is put into correspondence to a unique event lx in L in an invariant and unambiguous manner; the set of all yО U mapped into this lxО L, is called the set of events SIMULTANEOUS TO x AND EACH OTHER in the universal. The basic convenience is concealed in the addition "and each other" meaning the TRANSITIVITY OF SIMULTANEITY. If there is no transitivity, who needs that simultaneity?

In a non-Newtonian world everything becomes more complicated. The trouble is that everybody has his own past. Certainly in the Newtonian world some events had different pasts. For instance, the past of Kai Julius Caesar was not the same as that of Napoleon Buonaparte: that of the Corsican contained also Carl the Great who could not appear in Caesar's past for a single instant of his existence. However, the Newtonian world is well arranged in the following sense: for each instant there is a set of simultaneous events such that any two of them have a common past. Say, if the instant of mine on the Earth and that of my brother in mind at Syrius are synchronized, then, provided that the ordering is Newtonian, we have a common past and also a common future. Unlike that, in a non-Newtonian world (in particular, in relativity theory), whatever our synchronization is, my past and that of an alien will ALWAYS be DIFFERENT.

Therefore any definition of "simultaneity" in a non-Newtonian case based on the concepts of "the past a^- " of the event a (or its future, a⁺) is condemned to be intransitive and hence ineffective. In particular, if we called the events x and y simultaneous as long as yП x^- & yП x⁺ and, in addition, required that this definition be transitive, then very soon we would come to the conclusion that any two events in the universal are simultaneous. That is what explains the unfruitfulness of Robb's definition of simultaneity: he attempted to call two events simultaneous if they are connected by a light signal (yО ¶ x⁺ ).

To surmount this difficulty, a logical complication of the simultaneity relation has been invented. We have been saying that x is simultaneous with y assuming that the simultaneity relation is BINARY (bivalent), is a two-sided (binary) predicate. One of the achievements of relativity was the establishment of the fact that in a non-Newtonian world a BINARY TRANSITIVE predicate for explicating "simultaneity" is impossible. THREE-SIDED predicates have appeared for that purpose. Namely, one says that x is simultaneous with y in the frame of reference. It is convenient to consider both versions of this relation: for inertial particles and for an arbitrary frame of reference W (at the differential-geometric and vector levels of study).

To this end let us point out that when carrying out a consideration at the second or third level, it is possible (starting from only an order relation p ) to introduce correctly a definition of ORTHOGONALITY. Namely, one can speak of a hyperplane orthogonal to a straight line L, or of a hypersurface orthogonal to a congruence of curves W (a matter flow). In the present article we are not going to be involved in the subtleties of when those orthogonal hypersurfaces EXIST. From an external viewpoint the hyperplane la orthogonal to the timelike straight line L at the point a can be described solely in terms of an order relation:

l_a = {xО u| $ p$ q$ L' a,p,qО L' & L' ║ L & pa = aq & xО ¶ p⁺З ¶ q^-}. (3.1.1)

Here the sign ║ denotes parallelism of straight lines, the entry pa = aq means that the (affine) lengths of segments on L’ are equal. A vector structure is inevitably involved in this definition due to the notion of a straight line. The formula (3.1.1) describes the standard radar synchronization procedure: the scanned event is simultaneous with a(t₀) if the time elapsed while the signal travelled forth, pa(t0 - t1), is equal to that of its back travel, aq(t2 - t0). The radar simultaneity definition, interpreted as dating, is an extension of the interval dating by (2.5.1): given an event xО U\L’, we first ascribe a "smeared out", interval date (p, q)x referring to the observer L’, then put the temporates t1 and t2 (by the clock of the same observer) into correspondence to the end points p and q of that interval and finally ascribe a temporate to the event x by the a priori rule tx=(t2+t1)/2. The necessity of the latter a priori requirement was disputed by A.Gruenbaum who suggested that a temporate be ascribed by the law tx=(1-e)t2+et1, with 0 < e < 1; however, a discussion on this matter requires many words and promises few results (Pimenov 1987).

DEFINITION 3.1.1. x is said to be simultaneous to y with respect to the observer L if xО l_y where l_y is determined from (3.1.1).

DEFINITION 3.1.2. x is said to be simultaneous to y with respect to the frame of reference W if there exist such observers g1 and g2 belonging to W that xО g1&yО g2 and both x and y are situated at the same hypersurface orthogonal to the congruence W.

The cumbersome appearance of these definitions is caused by the very essence of the matter, i.e., the non-Newtonian and consequently essentially nonlinear nature of the universal. A regraduation by (2.6.2) will inevitably emerge if one requires that the simultaneity in cosmology be determined by the radar method, that is, by (3.1.1).

In non-Newtonian worlds clock regraduations (see Section 2.6) are closely related to the simultaneity definition. We have already noticed in connection with Definition 2.5.1 that the events x and y can have equal temporates (tx = ty) in one time t ("be simultaneous with respect to the given functional time") but not equal in another time (). Thus clock regraduations in non-Newtonian cases are connected not only with the choice of a function but also with the choice of a "simultaneity surface" in the universal. It seems that Backman worked under the presumption of Newtonian ordering, therefore this consideration does not apply. However, Milne worked with a non-Newtonian ordering and thus a choice of simultaneity surfaces is significant for his results. It cannot be asserted that Milne only changes the scale into a logarithmic one.

Let us discuss Milne's (1948) results in this aspect in more detail. He considered the "explosive frame of reference", i.e., the situation when all the material points are at the starting instant at the same spatial point, then immediately begin to escape (certainly no quicker than with the velocity of light) and later move just by inertia. If a single observer L is selected from this system W, one can speak of two simultaneity relations: as applied to an inertial particle (a straight line L), one can use Definition 3.1.1, while as applied to the whole system, Definition 3.1.2 should be used. In the first case the set of mutually simultaneous events is a hyperplane, while in the second case it is a (pseudo-Euclidean) sphere, i.e., the orthogonal section of a bundle of straight lines originating from a single point (Fig.4). Milne defines the temporate t by projections along planes and the temporate t by projections along spheres and only then uses his logarithmic transition. The main thing is that he operates with DIFFERENT simultaneity surfaces. Just this enabled him to show that both views are to be treated on equal terms: in the first one the whole world is represented by an expanding universe with a finite volume, which emerged a finite number of years ago and carries the Euclidean spatial geometry. The second one depicts a stationary world infinite both in space and time, with unchanged distances between galaxies, while the space has the Lobachevsky geometry instead of the Euclidean one. It is of importance that in both pictures the observable fact, the "spectral redshift", is present, although it is explicated by different pictures in different ways. It is a significant contribution into the foundation of conventionalism, not to be compromised by inaccurate presentations reducing everything to just a transition to the logarithmic time scale.

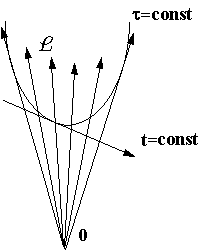
Fig. 4.

Milne himself did not touch upon the question of how his theory would work if the underlying universal were ordered in the Newtonian manner. It turns out that the paradoxical appearance of the result would decrease but some unexpectedness would remain. The point is that by the Newtonian ordering at the vector level a sphere coincides with a plane (the so-called semi-Euclidean geometry), therefore practically only a logarithmic transition remains, like that in Backman's case. Two views (conventions) are possible. In the first one the world is imagined as a Euclidean universe of infinite volume, which emerged a finite number of years ago and is uniformly growing. In the other one the world is Euclidean, with an infinite volume, but stationary and eternal.

Another example will be taken from geology. Sometimes the simultaneity relation is imposed by the very nature of the studied object, as in the case of a layer (a stratum) in geology. It is so natural to call everything in a single stratum, clearly undisplaced and with no traces of layer mixing, SIMULTANEOUS - and people do call it this way. However, in this case some difficulties appear. Consecutive layers contain both geological and biological remains. The corresponding datings are carried out, separately geological and biological ones. In our terms, the universal is supplied by two clocks, tg and tb :

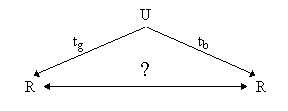
However, sometimes there is no correspondence between the readings of these clocks, i.e., there is no transition from the readings of one clock to those of the other which would preserve the order (The Rhythms of Space and Time, 1974). It sometimes happens that tg (p) < tg (q) but tb (p) > tb (q). How can one explicate such a situation? Let us first follow the logic of the authors of the cited book which led them to the idea to consider non-Newtonian orderings.

Let us suggest a clearer example. Consider a man whose age is measured, on one hand, by the number of shirts he has worn out and, on the other hand (or by the other clock) by the number of his meetings with a policeman. Can it happen that by the instant p he had worn out 500 shirts and had met a policeman 11 times but by the instant q he had already worn out 550 shirts but had met a policeman only 9 times? Our resolute answer will be "no". That would be contrary to logic and arithmetics. Can something of that sort happen in stratigraphy? Based on what reason? If the components of the layer represented the result of a LINEARLY ORDERED process (like the man in the above example), then in stratigraphy it would also be impossible and we would be obliged to treat the empirical data erroneous. An 'observer" is linear. However, if we believe that layer formation is a result of MANY linear processes ("matter currents" from Section 2.7), then new logical possibilities come into play. Say, there is a remnant of a cockle-shell p dated tg(p) geologically and that of another cockle-shell p' dated tb(p') biologically; there is also a petal imprint q dated tg(q) geologically and another imprint q' dated tb(q') biologically. It is known that p and p' are simultaneous and q and q' are also simultaneous. Can it happen that

tg(p) < tg(q) & tb(p') > tb(q')? (3.2.1)

If the ordering is Newtonian, so that tb(p') = tb(p) and tb(q') = tb(q), this cannot happen, as before, if the theory is to remain free from contradictions. However, if the ordering is Einsteinian, then tb(p') and tb(p) are not necessarily connected by an equality if p and p' are simultaneous. The same holds for t_b(q) and t_b(q') . Therefore the conjunction (3.2.1) is quite possible. Essentially that was the reason (although their arguments are not expressed in the same way) why K.V.Simakov (1982) and S.V.Meyen (1982) were inclined to admit that models of special or even general relativity ought to be used in an explication of empirical stratigraphy. They meant not only zones unattainable for a signal but even space-time curvature effects.

Such assumptions are not logically contradictory but need some immediate stipulations. First, one can then speak no more of a binary simultaneity: one has to consider a layer as a set of geobiological findings simultaneous with respect to a certain FRAME OF REFERENCE. As long as such a frame of reference is not specified, any appeal to relativistic models is incorrect. Second, because of the small sizes of the objects under study, while the velocity of light is so great, make it hard to understand where do those clearly observed deflections from the Newtonian ordering come from.

We believe that the A-transformations (Section 2.8) explicate the situation in a simpler way. The events p' and q' are situated on the world line of the object ("taxon" by Meyen) A, while the events p and q are on the world line of the taxon B. According to (2.8.1), the "own proper" geological time for p and q has the values of q g(A, t1) and q g(A, t2); respectively, the biological one is q b(A, t1) and q b(A, t2). Similar relations hold for object B. There is nothing unexpected in the fact that q g(A, t1), q g(B, t2), q b(B, t1) and q b(A, t2) can be connected by most various inequalities, despite t1 < t2. In particular, it is possible that q g(A, t1) < q g(A, t2) while q b(B, t1) > q b(A, t2). In terms of our illustrative example that would look as follows: the man A could wear out 500 shirts and meet a policeman 11 times during the same period when another man (B) wore 550 shirts and met a policeman only 9 times; and both got into the same common grave.

One of the usual negligences of word usage in the "problem of time" is that the term "time" is sometimes used as the name of an object (a "one-sided relation"), sometimes as the name of a function of a single variable (the time value t at a given event x, i.e., a two-sided relation, or a unary operation), and in other cases as the name of a function of two variables (the time t elapsed between the events p and q; as it was pointed out in connection with Definition 2.2.1, such a number is sometimes called "an interval"). The latter meaning of a "proper time" is sometimes used as a basis for building kinematics as a whole.

For the classical, Newtonian ordering such an interval is constructed in the following way:

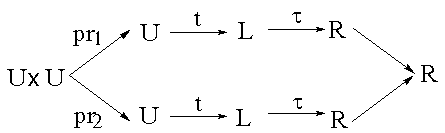
We thus have a mapping t of the universal onto a linearly ordered time t: U aL. If we want to speak of a function of two variables p, qО U, then we must form the product Uґ U thus obtaining tґ t: Uґ U a Lґ L. Assume that in the linearly ordered set (L,p ) (see Section 2.3) a certain temporal scale is given and clocks are graduated: t: L a R (see Section 2.5). The superposition of mappings t and t with a subsequent subtraction t° t(q) - t° t(p) makes it possible to ascribe a unique real number t(p, q) to the pair (p,q)О Uґ U. Thus the consecutive transition Uґ U a Lґ L a R is accomplished. The favourable properties of the Newtonian clocks provide the remarkable simplicity of the time interval between the events:

t(p,q) + t(q,r) = t(p,r). (3.3.1)

Let us mark the fact that for a cyclic time this relation must be understood locally.

The difficulties and ambiguities inherent in the selection of (L,p ) in (U,p ) applied to a non-Newtonian world have forced one to consider the direct mapping t: Uґ U a R, avoiding the intermediate linearly ordered set and the corresponding subtraction. This direct mapping was called METRIC and its result THE PROPER TIME INTERVAL, as opposed to an "improper" coordinate one. At the differential level of study the second-order derivatives of t received the name of the METRIC TENSOR.

It is entirely superfluous for our purposes to deepen into describing what is the "metric tensor". First, everything that is peculiar for the non-Newtonian case, can be described at the first, set-theoretical level of consideration without getting to the second one where the tensors live. Second, even at the differential-geometric level it is distinctly possible to do without the tensors as primary objects and without postulating the metric as a quadratic form. The matter is that (the main thing for a non-Newtonian ordering) one cannot do with a SINGLE clock (if the space-time dimensionality is greater than one, for instance, four). In the Einsteinian case there are always FOUR functionally independent clocks. And it turns out that postulating the existence of just four functionally independent clocks LEADS TO the existence of the needed metric tensor, unique up to a multiplier.

Let us return to the function t(x,y), i.e., t: Uґ U a R. Above all, to be able to speak of "a time interval", one must be sure that this function is an order type morphism, i.e.,

p p qЫ t(p,q) > 0 , (3.3.2)

while for pairs p,qО U unconnected by the order relation p this function is either just undefined, or is identically zero, or purely imaginary, or is identically -Ґ (there exist different versions of definition). Second, a specific condition must hold for t :

(p p q p r & p p r) Ю t(p,r) і t(p,q) + t(q,r) . (3.3.3)

This condition "extends" the equality (3.3.1) to an inequality, notably in a needed direction. If the reverse inequality

r(p,r) Ј r(p,q) + r(q,r) , (3.3.4)

were valid instead of (3.3.3), we would speak of a SPATIAL metric, whereas the inequality (3.3.3) makes it possible to speak of a SPACE-TIME (or kinematic) metric.

At the second, differential-geometric level of study the inequalities (3.3.3) and (3.3.4) are replaced, respectively, by the requirements that the quadratic form (the metric tensor) have the signature (+ - - ... -) or (+ +...+) (in the latter case the quadratic form is called positive-definite). At the third, vector level of consideration the same inequalities are replaced by the requirements that t be a concave function or r a convex function (of the vector variable in the corresponding domains), respectively. Here also some versions are possible: RIEMANNIAN geometry when the above tensor is DIRECTION-INDEPENDENT and FINSLERIAN geometry when it is DIRECTION-DEPENDENT. The latter metric is good for describing an anisotropic space-time. However, we would not like to fix upon that.

Thus, among all the mathematically thinkable functions, a very specific class can be connected with the label "time", namely, the functions satisfying the conditions (3.3.2) and (3.3.3).

An important point is that these conditions sharply restricts the whole immensity of possible clock regraduations. Here is an example for clarity: the equality (3.3.1) is a special case of the inequality (3.3.3). And as long as (3.3.1) holds, the whole diversity of clock regraduation is reduced to just a multiplication by a constant scale factor plus a possible displacement of the time zero point. By the way, this could be a good way of choosing a "true" time in the Newtonian case if the theory were constructed, instead of the traditional clock introduction on a linearly ordered set, axiomatically, using the condition (3.3.1). In the non-Newtonian case (3.3.3) is a weaker restriction but nonetheless it is far from the total arbitrariness of (R, <) ® (R, <).

As the space-time metric t has been introduced, each observer (material point, see Section 2.7) has a unique numerical measure of his (its) own time interval

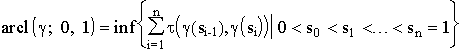. (3.3.5)

As soon as such an "arclength" g from g(0) to g(1) is found, one can select among all the possible point particles g the ones m for which the condition

(3.3.6)

is valid. Such point particles are called "geodesic" in the language of geometry and "inertial material points" in that of physics. Their properties are particularly good and the space-time studies are reduced to a great extent to studies of the behaviour of these particles. In particular, they are used when such notions as a relative velocity of two particles, curvature of a domain and others are introduced. Some of the effects of attraction and repulsion can be modelled with the aid of theorems on inertial particles. To do that it is quite unnecessary to pass to the more complicated differential-geometric level of study.

However, in order that a function of two variables from the universal could pretend to such a role, the universal must already be equipped with a structure of order p and, moreover, the conditions (3.3.2) and (3.3.3) must hold. Since in the papers by A.P.Levich (1989; see also his chapter in this book) neither of these steps is made, it is unclear whether his procedure of ascribing a "proper time interval" has something to do with a mathematical theory. Using his procedure, one can ascribe a "proper time interval" to two states of a multi-level kaleidoscope. But, whatever number or set of numbers (A.P.Levich measures time intervals by a SET OF NUMBERS rather than A NUMBER due to the multi-level nature of his systems; this complicates the verification of the permanance principle validity but this difficulty seems surmountable) could be ascribed to the difference of two states of a kaleidoscope, that has hardly anything to do with the problem of time.

There are different ways of obtaining t; we have described the AXIOMATIC one. Traditionally the metric t is derived from the group-theoretical axioms at the linear level of consideration combined with the differential-geometric ones at the second level. The original approach due to Milne, further refined by Walker and Schutz (Schutz 1973), is also of interest. Milne studies (see Section 3.2) his frame of reference W. Each observer L has his own clock entirely independent of the clocks of other observers. However, in the spirit of a "public treaty" the observers exchange light signals ¶ x+ and seek a unified time which could satisfy the natural axioms connecting the "native" time and the signal functions. These axioms turn out to yield just two solutions: the time t and the time t as described in Section 3.2. It is of great significance (although unmentioned by the researchers of that school) that the space-times where the sought unified time exists, i.e., where the above axioms are consistent with each other, are very rare. It turns out that the Milne-Schutz axioms can work only in the linear case (speaking technically, in zero curvature spaces). However, in this case the metric is determined uniquely.

Another remark here refers to the combination of RANDOMNESS and the metric. B.S.Fleischmann (1986) was absolutely right to note that in any real physical space-time metric measurements unremovable noise is present and, as long as the theory is unable to take this noise into consideration, it cannot be called an entirely justified one. Unfortunately, it is just the case for space-time theory. In the frames of the purely spatial metric theory with the condition (3.3.4) Schweitzer and Sklar (1983) managed to develop a "random metric" model. However, a similar "random space-time metric" under the condition (3.3.3) cannot be developed.

These unprecise words are applied to two situations: that of closed ("cyclic") time (see Section 2.3) and that of the automorphisms described below. Namely, the following transformations can be considered at the vector-linear level:

(3.4.1)

where t is the temporate and the radius-vector of an event. It turns out that a great number of physical theories are INVARIANT UNDER TRANSFORMATIONS (3.4.1). Thus, if a theory deals with wave equations including ¶ ²/¶ t2, the expression remains unchanged under (3.4.1). If it deals with the metric , it is also unchanged under (3.4.1), and so on. Therefore the "time reversibility in fundamental physical theories" is often discussed. As the time dealt with in the empirical data is clearly irreversible, it is sometimes claimed that there is a dramatic discrepancy between theory and practice. Actually the situation is not so dramatic. First, other "fundamental" physical theories exist in which the transformations (3.4.1) are impossible, such as the heat transfer equation

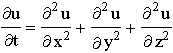. (3.4.2)

It is not invariant under (3.4.1), so that THE WHOLE EMPIRICAL MATERIAL CONNECTED WITH HEAT TRANSFER PHENOMENA CANNOT BE DESCRIBED IN TERMS OF REVERSIBLE TIME. Second, the automorphisms (3.4.1) themselves are defined at the vector-linear level of consideration (the third in our count, see Section 1.3). This level corresponds to a space tangent to the world, therefore the presence of (3.4.1) corresponds just to the differential-geometric fact that any smooth curve is symmetric at each point at the infinitesimal level, while globally the same curve is not obliged to be symmetric at any point. An example of a "fundamental physical theory" exactly repeating this property is the Friedmann-Gamow cosmology: the conditions (3.4.1) are valid for each point of the tangent space while globally the cosmological evolution is irreversible, i.e., possesses no automorphisms along the temporal coordinate. Third, even in such a highly symmetric theory as special relativity automorphisms are possible only if the anisotropy is entirely neglected. V.I.Vernadsky insisted that the space-time is anisotropic, so that isotropic models are just the first idealized approximation. Now mathematically correct anisotropic space-time theories have been built (Pimenov 1987) and they do not involve time reversibility (automorphisms (3.4.1)) even if the anisotropy is so small to be discovered experimentally.

Mathematically an anisotropic world is more complicated. Thus, one has to distinguish orthogonality from perpendicularity, i.e., the definitions of simultaneity using (3.1.1) cannot work, it is intransitive, etc. However, philosophically the inclusion of anisotropic worlds destroys the confrontation sometimes found between physics and biology: it is claimed that time in physics is reversible, unlike that in the living nature. This difference disappears, leaving just a difference between more and less idealized models.

We have mentioned that the possible non-Newtonian ordering, along with the forced character of the transition from the linearly ordered time with (3.3.1) to a more complicated universal with (3.3.3), comes into play only when we mean that there is something placed in as though quite another chest labelled "space". How can one imagine a space applied to, e.g., biology? As a number of indicators, each having a numerical value, i.e., the thing which Ashby (1956) called "a vector in cybernetics". For instance, those can be quantitative taxonomical characteristics, or a set of genes admitting a quantitative activity measure (by enzyme activity or by phenotype measurements), or other "vectors". The position of an individual (or a phenotype, a species, i.e., of an object under study) is described by a vector. The choice of a fixed nomenclature of quantitative indicators makes it possible to add these vectors and multiply them by numbers (separately for each position). As far as an order type relation in such a universal is undefined, differences between these individuals (given by vector differences, meaning either replaced element numbers, or by a metric r from Section 3.3, or in another form) supply us with information on SPATIAL DISTANCES, in the discussed example it is a biological distance in the biological space. As soon as the "earlier-later" relation is introduced for some pairs of individuals, so that the universal becomes partially ordered, the difference between individuals preceding one another becomes a metric in the biological space time. It can happen that some new indicators must be added to the nomenclature to make such an ordering possible.

If the indicator space is defined, one has a right to speak of the INDICATOR CHANGING RATE. In addition to the remarks made in Section 2.8, one has to remember that such a rate, or velocity, can be "average", "finite", for instance, Dx/Dt, Dy/Dt, Dz/Dt, when the "indicators" are the usual spatial axes, and "instantaneous", "differential", for instance, dx/dt, dy/dt, dz/dt in the same space. The admitted rate values are most closely connected with the ordering character in the universal: if and only if the ordering is Newtonian, dx/dt, dy/dt and dz/dt are entirely unbounded, i.e., can take any real values. On the contrary, if there exist the constants c1, c2, c3, c4, c5 and c6 such that c1 < dx/dt < c2, c3 < dy/dt < c4, c5 < dz/dt < c6 then the ordering is necessarily Einsteinian (the requirement c1= c2= ... = c6= c is just a special case and change nothing in the essence). Maybe some indicators involve the bounds (dx/dt) while the others do not (de/dt, see Example 2.2.3), then the ordering is neither Newtonian nor Einsteinian.

In our view, the work on the development of the time concept in biology must proceed side by side with the work on the development of the biological space concept. And while there can be controversies on whether or not it is reasonable to speak of a "biological time" or it is just a result of a certain A-transformation (2.8.1), as far as the biological space (or biological space-time) is concerned, no controversy can arise. Evidently the three physical coordinates x, y, z are INSUFFICIENT for describing biological differences between individuals, or relative remoteness of genotypes and phenotypes, and so forth. One of the aims of writing this essay was to convince the researchers that a way to creating a self-consistent and effective concept of "time in biology" is not STRAIGHT FORWARD: the concept of SPACE IN BIOLOGY was first constructed and only then the latter was reworked to form the concept of SPACE-TIME IN BIOLOGY.

Let us illustrate the capabilities of the theory by an unpublished example, considering the commonly accepted notion of biological space. Milne (1935) introduced the above (Sections 3.2 and 3.3) regraduations and signal functions on the background of a very specific theory where solutions to certain functional equations were sought under the invariance condition with respect to a certain group of automorphisms; something of that sort is done today in the theory called "physical structure theory". Thus, for instance, if t is a temporate, is a coordinate vector, is a velocity and is an acceleration, Milne seeks a function = (t, , ) invariant under the Lorentz transformations. He has also treated more complicated functions, like functions of a domain. We are not going into details of these considerations; it is sufficient to say that just the LORENTZ transformations did not turn out to be a specific feature of Milne's theory: I was able to extend it to the Newtonian case and some other groups. This model (in its Newtonian or Einsteinian version), if substantially interpreted in terms of astronomy, looked as a system of galactic nuclei which originated from a common starting point and escape in time; there appear condensations around each nucleus, while in spaces between the galaxies the voids are growing and there becomes less and less matter.

Assume now that we know what is the biological space. Then the same mathematical model admits, instead of the physical one, a BIOLOGICAL INTERPRETATION: once in the past all individuals were practically indistinguishable from each other (by biological indications) but eventually they split into groups which in due course DIVERGE more and more, increase their differences, and the INTERMEDIATE FORMS DISAPPEAR. Such a mathematical approach does not require any assumptions of "which mechanisms" cause that "formation of species", or whether there is an "evolution from simple to complex" or the reverse. The only significant mathematical requirement is the existence of a rich group of automorphisms ("symmetries") and a set of functions invariant under these automorphisms. The first requirement would correspond biologically to the EQUAL RIGHTS of different biological species (genera, classes): in this theory there is NO PRINCIPLE DIFFERENCE between mammals and bacteria, or between reptiles and protozoa, in the same way as in mechanics there is no difference between a laboratory at rest, the one falling to the sun and the one flying at a subluminal velocity. The second requirement would mean the EXISTENCE OF INVARIANT BIOLOGICAL LAWS. I obtained this result in 1959 but did not publish it because the mathematics there was trivial, the biology was heretical, while a generally accepted notion of a biological space did not exist.

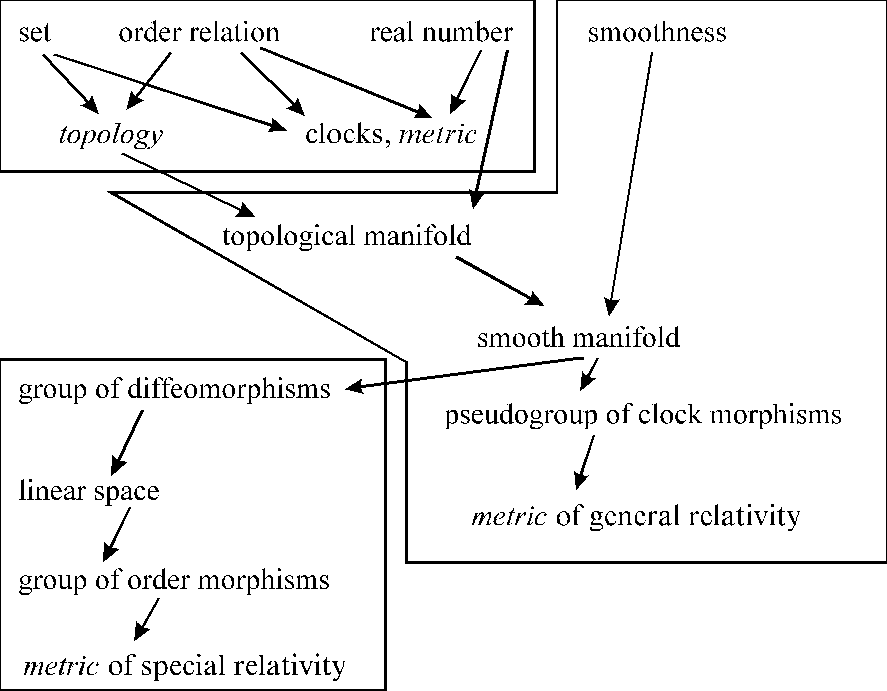
Fig. 5

Consider the scheme presented in Fig.5. The primary, underived, "a priori" notions are placed at the top. The arrows indicate the places where axioms are formulated in terms of the notions situated higher. The concepts that can be derived from Einsteinian ordering but not from the Newtonian ordering condition, are underlined.

Modern physics works in the differential equation paradigm. Therefore at the first (set-theoretical) level it is possible to formulate only the fragments of physics containing no differential equations in principle (for instance, one can consider integral equations irreducible to differential ones). At the second, differential-topological level the key point is the following. Assume that the differential equations governing the process are known. Assume further that at time t = t0 all the quantities contained in those equations are also known. Then mathematics provides the possibility to calculate all these quantities at t > t0 and thus "predict the future". In mathematics all that is called "the Cauchy problem", although Laplace had already used such a set-up (Fig.6). Figure 6 shows how the data are "carried away to the future" from the surface t = t0 by a causal influence. This implies the logical necessity of defining a "future of a set" in a rigorous way. Clearly there is no causally allowed displacement along the surface t = t0 itself. Thus a definition of an "achronous surface" is necessary. Finally, if nothing can affect the future t > t0 with the "initial data" surface t = t0 avoided, these initial data will determine everything in the future. This is the connection between the formalism of the mathematical Cauchy problem and its physical understanding in terms of causality and determinism.

Fig. 6.

Here is the sequence of the corresponding definitions dealing only with the order relation <.

DEFINITION 4.2.1. Given a set A, its FUTURE is the set A+defined as {x| $ aО A a < x}, i.e., A+= И a+ for aО A М U. The past A_ is defined similarly.

DEFINITION 4.2.2. Given a set A, its SATURATION AЕ into the future is defined as AЕ = AИ A+. Similarly for the past A.

DEFINITION 4.2.3. The set ¶ AЕ called the future CAUSAL BOUNDARY of the set A. That means that if xП (here a bar denotes the closure in the interval topology), then nothing occurring in A can affect x.

DEFINITION 4.2.4. The set AМ (U,<) is called ACHRONOUS if xП & yП holds for any x,yО A (sometimes the version щ x < y &щ y < x is used).

If we dealt with a functional time t: U a R , by its definition (2.4.1) from x < y it would follow that tx < ty and therefore such two points would not belong to the surface of simultaneity t = const. That is what Definition 4.2.4 expresses without appealing to tО R^U. All the surfaces of simultaneity which we defined in Section 3.1 are achronous in the above sense.

DEFINITION 4.2.5. Let A be an achronous set. The decreasing sequence ...< pk < pk-1 < pk-2 < ... < p2 < p1 whose first point p1 = p lies in the future A+ of A, is called EXTRANEOUS of A if pkП A and (pk, pk-1) З A=Ж for all k і 1.

What is the meaning of the chain ...<pk<pk-1<pk-2<...<p2<p1=p? It is the chain of consecutive causal influences from the past pk_ to the future p+. These influences are completed AFTER the set A (pО A+, i.e., $ a aО A & a < p). Naturally those chains of influences which ESCAPE A both themselves and by their intervals (pk, pk-1), pass ASIDE from A.

DEFINITION 4.2.6. It is said that an event pО A+ DEPENDS ON A if A is achronous and not a single sequence, extraneous of A, passes through p.

DEFINITION 4.2.7. The set of all pО U depending on A is called the future CAUCHY DEPENDENCE DOMAIN of A, denoted by D+(A).

DEFINITION 4.2.8. The set A is called a CAUCHY SURFACE for the future if any pО A+ depends on A; in another notation: A+= D+(A).

The meaning of these definitions is simple. If pО A+, this means that an event aО A CAN AFFECT p. However, are the expressions "can affect" and "determines" equivalent? No, since if p can also be affected by b and c which are in no way caused by A, we are very far from the situation "the set A determines the condition in p". Definitions 4.2.5 - 4.2.8 taken together give a definition of the situation when the future is affected by solely the events from the set A, that is, nothing else, uncontrolled by them, can exert an influence.

In a similar way D_(A) is defined. The boundaries of these sets (¶ D+(A)) \ A, (¶ D_(A)) \ A are called Cauchy horizons. They separate the causally disconnected parts from the rest of the space-time.

It should be noted that this terminology works in full power just in the case of the Einsteinian ordering, while for the Newtonian one it "skids". Moreover, for its effectiveness some more special postulates must hold, though they are irrelevant here.

A topological manifold can be defined under an Einstein ordering already at the first level of consideration: there is a topology (the interval one), there are real numbers and nothing prevents one to introduce the axiom that each point has a neighbourhood homeomorphic to Rⁿ , where n is called the number of dimensions. The things are not so simple with smoothness, the notion of necessity for the second, differential-topological level of consideration. It appears as follows. From the whole set of continuous functions from U to R (where U is already regarded as a topological manifold) we select a SUBSET OF FUNCTIONS F М R^U called (provided that it satisfies certain axioms) the family of smooth, or differentiable, functions, or, in short, the "smoothness". After the smoothness has been fixed, we acquire the right to formulate differential equations and to apply their conclusions. Here is the point where the definitions of Section 4.2 work.

And at that point a transition from three to four dimensions turns out to be fateful. As long as we are dealing with the space (x, y, z), the SMOOTHNESS IS UNIQUE. However, when we pass to the 4-dimensional manifolds, i.e., to SPACE-TIMES, it turns out that there EXIST DIFFERENT smoothnesses on the same manifold, which are not diffeomorphic to each other. More than that, even on the simplest and natural manifolds, like R⁴ , there exists an infinite number of undiffeomorphic smoothnesses (Gonut 1983). Dealing with the equations like 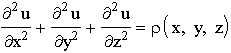one can even not mention the smoothness due to its absolute character: in that case the smoothness considerations are purely technical and are of interest only for mathematicians. However, in the equations like 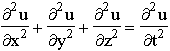, by virtue of the RELATIVITY OF SMOOTHNESS the latter gains a significant meaning unclear for physicists: in a transition from one smoothness to another the derivatives which occurs in the equations are not transformed linearly (or in ways derived from linearity); the results will not be isomorphic; and there is no physical ground to favour one smoothness over another.

On the other hand, smoothness is absolutely necessary in the key aspect discussed in Section 4.1. It is the differentiability that permits us to draw the "matter current lines" (or "the lines carrying the causal influence") for an infinitesimal interval dt after t = t0 as a family of parallel lines (see Fig.6). If the functions were not differentiable, at least one of the lines would "break", become a broken rather than a straight line. That would violate the "sedate" character of interaction transport: at a point where the broken line transfixed another line, a single event would be affected by two different, uncoordinated factors, i.e., there would be an AMBIGUITY. We need a smoothness but what is smooth in one smoothness turns out to be unsmooth in another: which of them is "true", "corresponds to the physics of the process"?

If one tries to "give up smoothness as hopeless" and include unsmooth structures into consideration, one immediately encounters enigmatic objects like Kantor's "devil's ladder". For instance, in a Newtonian universal a material point can exist which moves translationally in a single direction and advances forward; its instantaneous velocity EXISTS NEARLY EVERYWHERE (i.e., up to a set of measure zero, with a "zero temporal duration" subtracted) and at all instants when this velocity exists, it EQUALS ZERO. A point advancing forward with a constant zero velocity?! It is hard to imagine, but it is one of the first, simplest troubles which we meet when leaving the cosy class of smooth functions.

Since the times of Laplace, who first claimed the determinacy of the mechanical phenomena (apparently meant already by Newton) as a fundamental fact in the world structure, various directions in physics have emerged, trying to CIRCUMVENT this determinacy. These are the thermodynamic direction, which has expressed itself most completely in quantum physics dealing with infinite-dimensional "space of states" rather than the space-time manifold R⁴; the statistical direction involving the ideas of randomness and noise; the discrete direction which forbids infinite splitting-up and consequently the very paradigm of the differential equations.

However, in mechanics, hydrodynamics (general relativity, even its Finslerian generalization, is hydrodynamics by its structure) and electrodynamics the deterministic views were preserved, although subject to refinements like those made in Sections 4.1 and 4.2. The results are now presented not with the quantifier "in the whole world" but with the remarks like "If the initial data are given at the Cauchy surface for the future and the governing differential equations are known, then in the future, in the Cauchy dependence domain..." and further it is claimed, as before, that all the quantities involved in the equations are determined in an unambiguous way.

This formulation is killed by the existence of unisomorphic smoothnesses. The fact (discovered only in the second half of the 20th century) that not a single Cauchy surface is possible under the Newtonian ordering, since for any surface t = t0 there is an extraneous sequence, for instance, (t, x) with x = 1/(t - t0), kills this idea in the history of science as well. Newtonian mechanics is constructed so that at any instant the God (or a devil, or a demiurge) COULD through a material point from an infinitely long distance with an infinite velocity in such a way that it would affect all the events after t0, already with an allowed finite velocity, thus mixing the influences from everything given at t = t0.

It looks as if we have to admit that the idea of determinacy has no ground. Accordingly, the traces of influence of this idea upon nonphysical sciences should be revised. Those traces are vast - from the views of the "iron" determinacy of the historical processes to similar views concerning the processes studied by biology.

A more detailed presentation of the ideas outlined in the present chapter is contained in the author's book (Pimenov 1991).