By the fundamental postulates of causal mechanics, a cause and an effect are separated by arbitrarily small but nonzero space (d x) and time (d t) differences, with the time difference being of a definite sign since an effect comes after a cause. N.A.Kozyrev has called the ratio of these quantities the course of time c₂:

c₂ = dx/dt . (4.1)

The proposition that a cause and an effect cannot be spatially superimposed is used in classical mechanics as well. This proposition follows from Newton’s third law according to which the forces of action and reaction are applied to different bodies, meaning that there necessarily exists a nonzero spacing between the force application points. At the same time classical mechanics neglects the time difference between the cause and the effect. It is also apparent in Newton’s third law, where the forces applied to the cause and the effect act at the same instant. Thus one can say that classical mechanics is a degenerate case of causal mechanics corresponding to the following values of quantities: d x№ 0, d t=0 and c₂=Ґ (Kozyrev 1991).

Neglecting the time difference between the cause and the effect leads to inaccuracy of setting the directions and magnitudes of forces in classical mechanics. Let us show that.

Assume that the four-dimensional proper Euclidean space is a geometric image of space and time (which is known not to be contrary to classical mechanics). Since the four coordinates in this space should be measured with the same units, we assume, by analogy with the theory of relativity, that the time coordinate is ct, where c is the velocity of light in vacuum.

In the present section we shall interpret the quantities п d xп and п d tп differently from what was done in Section 1. These quantities will be considered to be determinate, i.e. taking quite definite values for specific cause-and-effect links, which may, however, be different for different links. It is this treatment of the above quantities that was used in N.A.Kozyrev’s papers (which is to be judged only from the context, since this issue was not discussed in detail by Kozyrev (1991)). We shall assume that Kozyrev’s law

is valid, where a is the fine structure constant (a » 1/137). It should be emphasized that in what follows our attention will be focused on “classical” forces, while the additional ones, considered in Section 3, will be discussed only at the end of the present section.

The fact that the cause and the effect manifest themselves at different instants means that they belong to different hyperplanes of simultaneous events (Fig.6). This raises the question: “Where are the forces, applied to the cause and the effect, directed: do they lie in the corresponding hyperplanes of simultaneous events or are they directed along the straight line connecting the cause and effect points?” Classical mechanics does not allow one to make a choice between these possibilities. Therefore we make use of considerations of symmetry. Since the cause-and-effect link incorporates a rotation axis, passing through its points, as an element of symmetry, it is natural to expect that the force system connected with it, has the same symmetry. This gives a ground to believe that the interaction forces are directed along the straight line connecting the cause and the effect, as shown in Fig.6. Such an orientation of forces fits the relativistic symmetry of space and time as well. (Note that this consideration does not apply to the additional forces of Section 3, since the symmetry of the latter is determined by the properties of not only the cause-and-effect link but those of time as well.)

— the cause-effect interaction force; — the temporal component of the force ; — the component of along the hyperplane of simultaneous events; ï d xï , ï d tï — the spatial and temporal intervals between the cause and the effect at a causal interaction; t — the time axis; H₁, H₂ — the hyperplanes of simultaneous events, passing through the cause and effect points, respectively; M_cC — the world line of the cause (only its part up to the instant t is shown); M_eM¢ _e — the world line of the effect; E₀ — the intersection point of the hyperplane H₁ and the world line of the effect; E¢ — the projection of the effect point E on H₁; c — the velocity of light in vacuum; it has been taken into account that the effect occurs later than the cause; the hyperplanes H₁ and H₂ are drawn with the dimension reduced by one.

Fig.7. The projections of a cause-and-effect link onto hyperplanes of simultaneous events passing through the cause point C (a) and the effect point E (b):

Being directed as described, the interaction forces have a nonzero temporal component neglected by classical mechanics. Let us find a relation between this component and that lying within the hyperplane of simultaneous events. As a straight line, being projected onto a hyperplane, passes to another straight line, the interaction force vector and both of its components lie in the (two-dimensional) plane passing through the three points: the cause point C, the effect point E and the point Eў (where Eў is the projection of the point E onto the hyperplane of simultaneous events corresponding to the point C). One of the components of the vector is perpendicular and the other is parallel to the segment CEў . Taking this fact into account, one can see from Fig.6 that the component directed along the time axis and the component directed along the hyperplane of simultaneous events are connected by the relation

.

Hence, using the law (4.2), we find

(4.3)

Thus generally the condition d t №  0 may result in the appearance of a time component of the interaction force. One of the inaccuracies of handling forces in classical mechanics lies just in neglecting that possibility.

In classical mechanics an inaccuracy of force representation is also present due to neglecting a mutual displacement of the cause and the effect taking place during the time interval d t. Let us estimate this inaccuracy.

In classical mechanics it is assumed that the cause and the effect happen at the same instant. This means that the interaction forces are applied at the points of the world lines of the cause and the effect located at the same hyperplane of simultaneous events. If d t № 0, then such a hyperplane may be arbitrarily chosen among the hyperplanes placed between those of the cause and the effect (both are shown in Fig.6).

Let us analyse the extreme situations when just these two surfaces serve as the hyperplane considered in classical mechanics (Fig.7). The figure demonstrates that in these two cases the segment connecting simultaneous events of the world lines of the cause and the effect is directed differently and varies in length due to their mutual displacement (these are the segments CE₀ and C₀E in Figs.7a and 7b, respectively). The interaction force considered in classical mechanics is directed just along this segment and is unambiguously determined by its length. In the figure it is denoted by . At the same time the component of the real interaction force has another direction, namely, along the segment connecting the projections of the cause point C and the effect point E onto the hyperplane of simultaneous events (these are CE' and C'E in Figs.7a and 7b, respectively). Note that the line of action of the component is the same for any direction of the interaction force in the plane CEE' (see Fig.6), in particular, when a time component of the force is absent, i.e., for . It should be noted as well that the (two-dimensional) planes where the prototypes of the system of vectors depicted in Figs.7a and 7b lie, may be non-coplanar in the four-dimensional space; however, the straight lines belonging to those planes and labelled in the figures by the unit vector , are mutually collinear.

Let us first estimate the direction inaccuracy of the force , neglecting the inaccuracy of its magnitude.

Assume that the accelerations of the interacting points are so small that the world line segments passed by them for the time interval d t, are close to rectilinear. Then the projections of these segments (i.e., the lines E₀E' and C'C₀ in Fig.7) are close to rectilinear as well. Hence it is easily assured that the angles y ₁ and y ₂ between the forces and are expressed as follows:

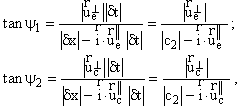(4.4)

where and are the components of the effect motion velocity, perpendicular and parallel to the force , respectively; and are the same for the cause; is the unit vector lying on the line of action of the force and directed from the point C (or its projection C') to the point E' (or E); here the law (4.2) has been used.

We shall assume that the velocities of motion of the effect and the cause are small compared with the constant c₂: п п < < п c_2п , п п < < п c_2п . Then, based on (4.4), one can write (in the linear approximation in п п /п c_2п , п п /п c_2п )

(4.5)

In this case the difference - is approximately described by the following formula for the two cases under consideration, assuming that the lengths of the vectors and are nearly equal (see Fig.7):

where g = sign(). The coefficient g sets the sign of the expression which depends on whether the cause and the effect attract (< 0) or repel (> 0) each other; the factors /п п and /п п serve as a direction unit vector setting the direction of the force -.

From the relations (4.6) it follows that the inaccuracy of the action direction of the force can be compensated by adding to it an additional force equal on the average to

(4.7)

The same relations imply that the extreme positions of the force _cl depicted in Figs. 7a and 7b differ by the value equal to

, (4.8)

where is the component of the motion velocity of the effect with respect to the cause (=-) perpendicular to the force . It should be noted that the quantity is of invariant nature since it is determined by the relative velocity of motion of the cause and the effect, whereas the quantity , being connected with the absolute velocity values, depends on the choice of the frame of reference and hence is not invariant.

Let us now estimate the inaccuracy of setting the magnitude of the force (neglecting the inaccuracy of its direction).

Consider a typical interaction law such that

, (4.9)

where f denotes all the relevant quantities except the distance; r is the distance between the interacting material points. By the postulates of causal mechanics, a spacing between the cause and the effect in interaction is п d xп . Meanwhile in the two cases depicted in Fig.7 the spacings r₁ and r₂ between the application points of the “classical” forces (i.e. the lengths of the segments CE₀ and C₀E) are other than п d xп and amount to

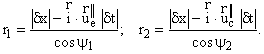(4.10)

In the case of п п < < п c_2п and п п < < п c_2п , as follows from Eqs. (4.5), the approximate equalities cosy _{1 »} 1 and cosy _{2 »} 1 are valid (in the linear approximation in п п /п c_2п and п п /п c_2п ). Based on the latter and the law (4.2), we obtain from (4.10) the following values of r₁ and r₂:

(4.11)

A substitution of these distance values into (4.9) gives the following values for the force magnitudes:

(4.12)

where F = f/п d xп ² is the real value of the “classical” interaction force magnitude.

From Eqs.(4.12) it follows that the inaccuracy of setting the magnitude of the force may be compensated by adding to it a supplementary force equal on the average to

, (4.13)

where it has been taken into account that the vectors , , and are mutually collinear and approximately parallel to the vector . From formula (4.12) it follows as well that the range of magnitudes of the force in these two cases is such that the corresponding differential force D is

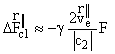, (4.14)

where is the component of the relative velocity of the effect parallel to the force . Here, as before, the force D is an invariant quantity, while is not.

Using (4.7), (4.8), (4.13) and (4.14) in practice, it is convenient to express the forces they set in terms of the mean value of the “classical” force. In the following just this mean value will be denoted by . Since these forces are small compared with , the formula obtained will remain valid (in the linear approximation in and , as considered), if one substitutes the real forces in them by their approximate “classical” value and, moreover, assumes that the velocity components denoted by the symbols ┴ and ║ are directed in perpendicular and parallel to the force but not to the force . Performing these changes, we conclude on the basis of (4.8) and (4.14) that the difference between the extreme values of the “classical” force can be presented in the form of a sum of two components, of which the first one is perpendicular and the second one parallel to the force :

(4.15)

, (4.16)

where g = sign(); F=п п . By (4.7) and (4.13), we arrive at the conclusion that the supplementary forces to be added to the “classical” force to compensate the inaccuracies of its direction and magnitude, are of the form

(4.17)

, (4.18)

the first one of these forces being perpendicular and the second one parallel to the force . Recall that the interaction law (4.9) was used in deriving Eqs. (4.16) and (4.18).

Let us unify all that with the temporal component of the interaction force, as it has been discussed earlier. From (4.3) it is easily obtained that

, (4.19)

where is a “velocity” of motion of our World along the time axis ( is parallel to the time axis, directed from the past to the future and has the magnitude c: п п  = c); here it is taken into account that the vector is pointed in the same direction as the vector in the case of repulsion and oppositely in the case of attraction (see Fig.6).

Thus in classical mechanics the interaction force proves to be inaccurately fixed due to a neglect of time difference in the instants of appearance of the cause and the effect. It has an error in the components values along the three mutually perpendicular directions: the time axis and two directions lying in the hyperplane of simultaneous events — along the force itself and perpendicular to it.

In Section 3 one more inaccuracy of the “classical” force, the one due to a specific action of time, was discussed. Let us write down all the four additives compensating the inaccuracies of the “classical” forces as applied to a particular case of the cause point being at rest ( = ). Using Eqs. (3.11), (4.17) - (4.19), we obtain

(4.20)

Here we have taken into account the following: (a) the cause-and-effect link as considered in Section 3 is actually a pair of simultaneous points on the world lines of the cause and the effect, therefore the points C and E and the force from Section 3 are, in fact, the points C and E₀ (or C₀ and E) and the force from the present section, respectively (cf. Figs.3 - 5 with Figs.6, 7); (b) Eq. (3.11) written for the case of =, = remains valid for № as well if one substitutes the quantity v (equal to ) by (since the component does not contribute to the force according to (3.6) and (3.9)); (c) = for = . Note that all the four additional forces are mutually perpendicular (recall that the unit vector is orthogonal to the vectors and ).

Attention should be drawn to the fact that all the formula of (4.20) are of the same kind. All the additional forces being described by them are, first, proportional to the absolute value of the “classical” force and, second, proportional to the ratio of the corresponding velocity to the constant c₂. This gives one more, if only indirect, argument in favour of introduction of the additional force ; at any rate in the absence of it the symmetry of the four linearly independent directions of space-time would have been violated.

Concluding the present section, we draw attention to a possibility of giving two different interpretations of the pattern depicted in Fig.6 (independent of whether or not the force has a time component). The first interpretation is based on the conception of our World as a three-dimensional hyperplane of exactly zero thickness along the time axis. In agreement with this idea the figure under consideration is an image of two states of the World separated by a time interval d t. Besides, there occurs an interaction between the future and the past states of the World. Another interpretation is based on the assumption of our World having nonzero thickness along the time axis or, speaking in the spirit of quantum mechanics, there is a “smearing” or “uncertainty” along this axis. In this case one might say that the pattern in Fig.6 depicts two interacting material points belonging to the same state of the World but lying in its different temporal sections.

REFERENCES