Time is one of the most fundamental ideas of physics. It, or, more precisely, the variable describing it (usually denoted by the letter t after the word “time”), enters into the equations of motion of Newton’s classical mechanics, Schrцdinger equation of quantum mechanics, the equations describing system evolution in thermodynamics and statistical physics and many other equations of practically all divisions of physics. Besides, time remains one of the greatest mysteries of nature. Such questions of principle as: “What is the stream of time?”, “Does the direction of time exist or not?” and a number of others have not yet been solved conclusively and rigorously.

Modern scientific world outlook knows two essentially different conceptions of time, the relational one and the substantial one (Chernin 1987; Molchanov 1977, 1990; Space... 1983). According to the first one, there exists no time “per se” in nature and time is no more than a relation (or a set of relations) between physical events. In other words, time is a specific manifestation of the properties of physical bodies and changes occurring in them. The second conception, the substantial one, assumes, vice versa, that time is an independent phenomenon of nature, a specific kind of substance, coexisting with space, matter and physical fields. The relational conception of time is conventionally associated with the names of Aristotle, G.W.Leibnitz and A.Einstein. The most ardent adherents of the substantial conception of time are Democritus, I.Newton and N.A.Kozyrev.

Nowadays physics is based exclusively on the relational conception of time. This manifests itself in the fact that only matter and physical fields are regarded in all physical theories as material objects, without any time substance of a “specific kind” involved. With such an approach it is impossible to determine purely logically, whether a time substance exists or not in reality, since it is impossible to prove the presence or absence of something which is not defined.

The aim of the present paper is to formulate the fundamentals of a physical theory based on the alternative, substantial conception of time. N.A.Kozyrev’s ideas about an active role of time in the phenomena of our World (Kozyrev 1991) impelled the author to do this work.

This section presents some data from linear algebra (Kostrikin, Manin 1986; Lang 1965; Mathematical... 1977-1985; Rashevsky 1967; Vakulenko 1972, 1992) and special relativity (Alexandrov 1988a,b; Brillouin 1970; Chernin 1987; Einstein 1905; Fock 1961; Hawking 1988; Kostrikin, Manin 1986; Landau, Lifshitz 1988; Logunov 1987; Mathematical... 1977-1985; Minkowski 1909; Okun’ 1989, 1991; Pauli 1958; Penrose, Rindler1984; Physical...1983; Polyakhov 1988; Rashevsky 1967; Sazanov 1988; Tolman 1969) to be used below directly or indirectly.

All physical events occurring in nature are ordered in a certain way. This is apparent from the fact that space and time localizations of events obey a strictly fixed law: they form a manifold possessing completely determined properties. It is usually called the space-time manifold or simply space-time. Within the problems solved by special relativity one may consider this manifold to possess the geometry of Minkowski space. Let us recall the corresponding definition.

The four-dimensional real pseudo-Euclidean space of signature (1, 3) is called Minkowski space. (Sometimes the signature (3, 1) is used.) Like any Euclidean space, Minkowski space comprises three elements: a basis set, a vector space with scalar multiplication of vectors, called the associated space to the Minkowski one, and a mapping assigning a vector of the associated space to each ordered pair of points from the basis set. With regard for such a construction Minkowski space is sometimes called a point-vector space. The vectors of the associated space and the points of the basis set are conventionally called vectors and points of Minkowski space itself, while the metric form defined on the direct product of the associated space with itself, is called the metric form of Minkowski space.

In special relativity it is conventional to denote by the term “Minkowski space” just the manifold formed by space-time locations of physical events, i.e. the space-time. The points of this manifold are called world points or events. (The latter reflects the fact that a “physical event” is understood here in an idealized sense, namely, as a position of a point object at a given place of space at a given time instant.)

It should be emphasized that in special relativity Minkowski space formed by points-events is treated as a physical reality but not just as a mathematical abstraction. It is of importance that Minkowski space is a unified manifold, unseparated into space and time, in which it fundamentally differs from our intuitive image of the Universe. The fact that we perceive time and space separately is related apparently to the specific character of our organs of sense (to which we adjust our physical instruments), lying in our ability to perceive only those characteristics of physical systems which correspond not to Minkowski space vectors themselves but separately to their spatial and temporal components. Note that the components of the same vector, calculated in different frames of reference, may take different values. It is due to this fact that the spatial size of a body or the time interval between two events may take different values being measured in different frames of reference, which is a well-known effect of relativity.

The metric form g, setting scalar multiplication of Minkowski space vectors, is a canonical real-valued non-degenerate symmetric bilinear form of signature (1, 3). The scalar multiplication operation is denoted by a point between the multipliers:

, (2.1)

where and are arbitrary vectors of Minkowski space.

It is known that any bilinear form T on a finite-dimensional vectorial space X may be regarded as a two-valent affine tensor over X. If a scalar product of vectors is defined on X, one can use the law: T(,) = Ч TЧ , to set up a correspondence between the form and the tensor. Here on the left-hand side of the equality T is a form and on its right-hand side T is a tensor; , О X. In just the same way any linear operator P defined in X may be treated as a two-valent affine tensor over X, with the correspondence between the operator or the tensor expressed by the law P() = PЧ , where on the left P is an operator and on the right P is a tensor; О X.

The above laws establish one-to-one linear mappings of the set of all two-valent affine tensors over X onto the set of all bilinear forms on X (in the first case) and onto the set of all linear operators in X (in the second case). It is of importance that these mappings are defined only by the inner properties of the sets being connected by them. In other words, these laws set up canonical isomorphisms between the sets. As is known, the presence of a canonical isomorphism allows one to identify the set elements connected by it. Therefore we have denoted the corresponding elements of the sets by the same symbol. It is needless to say that the canonical isomorphisms between these sets may be established by other laws as well, e.g., such as: T(,) =Ч TЧ , P() =, or T(,) = -Ч TЧ , P() = 2PЧ (note that generally Ч TЧ № Ч TЧ , PЧ № ). In what follows we shall use the laws written above.

The metric form g, according to the aforesaid, is at the same time a two-valent affine tensor, therefore it is also called the metric or fundamental tensor of Minkowski space. It follows from the above law of correspondence between the form and the tensor that the metric form g satisfies the relation

(2.2)

for all , , where the notation (2.1) is taken into account. Using this connection and the properties of the form g, one can prove that the form g, viewed as a tensor, satisfies the relations

(2.3)

for any vector and tensor T. From this and from the aforesaid about the connection between tensors and operators it follows that the form g is an identity (unit) linear operator, therefore it is also sometimes denoted by the symbol I: g = I.

By the properties of the metric form g the scalar square Ч of a vector may be positive, negative or zero. In the first case the vector is called timelike, in the second case spacelike, and a nonzero vector having a zero scalar square is called isotropic or null. Let be any four vectors of Minkowski space having nonzero scalar squares and orthogonal to each other in pairs (the latter means that for i № j, i,j=0,1,2,3). On the basis of the law of inertia, from the fact that the metric form g has the signature (1,3) it follows that among the above four vectors there are exactly one timelike and exactly three spacelike ones. The timelike vector is conventionally denoted by the index 0 and the spacelike vectors by the indices from 1 to 3. In such a numeration of the vectors .

If A and B are points of Minkowski space and and are their radius vectors, the scalar square of the vector =- is called squared interval s² between these points:

(2.4)

Sometimes the notion of vector length (magnitude) is introduced, defined as the number

(2.5)

where the non-negative value of the root is taken for Ч і 0 or its imaginary positive value for Ч < 0. The lengths of a timelike, spacelike and null vector are positive, purely imaginary are zero respectively. A vector with a length equal to unity (imaginary unity) is called unit (or, respectively, imaginary unit). Note that the vector length notion is introduced exclusively by convention, originating in the usual presentation of Euclidean geometry. The vector length notion is not intrinsic in the theory of Minkowski space because the root extracting operation is not used in a vector space. Moreover, this notion even involves a contradiction since Minkowski space is real and no imaginary values should appear in it. The notion of vector length can be eliminated from the consideration and replaced by that of the real-valued scalar square of a vector.

Due to the bilinearity of the metric form g the equation (k)Ч (k) = k²Ч is valid for any vector and real number k. Hence for an arbitrary vector the sign of the scalar squares of the vectors k is the same for all k № 0. Therefore in Minkowski space all nonzero vectors, belonging to the same straight line, belong to only one of the types: timelike, spacelike or null vectors. With regard to this straight lines are similarly called, in particular, a straight line containing a null vector is called null. The lines whose all tangent vectors belong to a particular type, are called in the same way.

The set of all null straight lines passing through a certain point O is called null or light (hyper) cone with the vertex at the point O (Fig.1); it is described by the equation

(2.6)

Fig.1. Cross section of a light cone by a two-dimensional plane passing through its vertex: One half of the light cone, G₁ or G₂, is the past cone, the other is the future cone; O is the cone vertex.

where A is an arbitrary point of the light cone; and are radius vectors of the points A and O. From Eqs. (2.4) and (2.6) it follows that the squared interval between any point of the light cone and its vertex is zero.

Each light cone divides Minkowski space into three subsets: the cone itself, being a three-dimensional hypersurface, the interior of the cone and its external domain. The maximum dimension of a Euclidean subspace passing through the light cone vertex, with all its remaining points located in the interior of the cone, is equal to unity. The maximum dimension of a Euclidean subspace passing through the light cone vertex and otherwise located in the external domain of the cone, is equal to three.

A certain line in the Minkowski space corresponds to each point material object and describes its time evolution. This line is called the world line of a given object. All the world lines of nonzero mass objects are timelike. All the world lines of zero mass objects (photons, etc.) are null.

Of utmost importance is the experimental fact of each line having an objectively distinguished orientation, indicating the direction of object temporal evolution. It is also important to note that the orientations of all the world lines are mutually concordant. The latter allows one to speak of the time stream direction, the same for all objects, and to introduce the concepts of the past and the future as objective characteristics of nature, independent of the choice of a direction in which the time coordinate increases. The physical manifestation of world line orientation concordance may be exemplified by the behaviour of photons radiated from a single space-time point: the world rays of all such photons are located only on one half of the light cone with a vertex at that point, although the other half is geometrically exactly identical to the first one (see Fig.1). The first of these halves of the light cone is called a future light cone and the second one a past light cone. This fact of the objective distinction and concordance of the world line orientations may be interpreted as the impossibility to realize in nature any solutions of dynamic equations corresponding to motion of objects from the future to the past. The prohibition of such solutions is sometimes called the principle of cosmological censorship. A physical mechanism underlying this fact is so far unclear.

A mapping of the Minkowski space onto itself, leaving unchanged all its points and vectors, is called the identity transformation.

We will call inversion of Minkowski space with respect to the point C the transformation of this space which reverses the signs of all vectors and transforms each point into the point symmetric to it with respect to C; the latter means that an arbitrary point A of Minkowski space is transformed into the point B such that =- (this equality is equivalent to - =- (- ), or =2- , where , , are radius vectors of the points A, B and C, respectively). The point C is called the center of inversion.

The identity transformation and the inversion of Minkowski space are one-to-one affine mappings of Minkowski space onto itself. Let us note that linear transformations of the vector space associated with Minkowski space are incorporated in these mappings. These transformations are naturally called the identity transformation and inversion of the associated space. These transformations can be expressed in terms of the metric tensor g viewed as a linear operator. Namely, the identity transformation of the vector space associated with Minkowski space is realized by the operator g obeying the rule:

(2.7)

while an inversion by the operator - g = (- 1) g:

, (2.8)

here is an arbitrary vector of the associated space and the first relation from (2.3) has been used.

Based on Eqs. (2.7), (2.8), one can write down: (gЧ )Ч (gЧ ) = (- gЧ ) Ч (- gЧ ) = Ч , where and are arbitrary vectors of the associated space. It follows that the identity transformation and inversion of the associated space leave scalar products of vectors unchanged, i.e., they are isometric transformations of this space. The latter means that the operators g and - g belong to the group of orthogonal transformations of the vector space associated with Minkowski space.

A shift, or translation on the vector , of Minkowski space is by definition a transformation of Minkowski space leaving all its vectors unchanged and transforming each point A into a point B satisfying the condition = (in other words, =+). A shift may be clearly imagined as a parallel translation of the whole Minkowski space by a vector . Note that with respect to the vector space associated with Minkowski space a shift behaves as the identity transformation. Similar to the transformations defined above, a shift is a one-to-one affine mapping of Minkowski space onto itself.

Motions of material bodies are always defined with repect to other bodies. Therefore in physics an important role belongs to frames of reference. Any of them is represented by a set of a clock and a (three-dimensional) system of spatial coordinates connected with a body with respect to which motions of other bodies are studied; this body is called a reference body.

Inertial frames of reference, i.e. the frames in which Newton’s first law is valid, correspond to the (four-dimensional) orthogonal systems of coordinates in Minkowski space. Let {x⁰, x¹, x², x³} be such a coordinate system with the origin at the point O, and {} be an orthonormal tetrad of this coordinate system (here x⁰ and are the temporal coordinate and the direction unit vector of the time axis; the remaining coordinates and vectors are spatial). By the properties of the metric form g and the definition of an orthonormal tetrad we have:

(2.9)

i.e., is a unit vector and are imaginary unit vectors (with the use of a metric form of the signature (3, 1) we would have Ч = - 1 and Ч =...= +1). Note that each of the unit vectors _i can be directed in any of the two possible directions along its coordinate axis; in particular, the unit vector , indicating the direction in which the time coordinate x⁰ increases, may be directed along the time axis from both the past to the future and otherwise.

By {⁰,¹,²,³} we denote the tetrad being mutual (dual) to the tetrad {}. It is defined by the conditions

(2.10)

From Eqs. (2.9) and (2.10) it follows that the mutual tetrad unit vectors are expressed in terms of the starting tetrad vectors as follows:

(2.11)

Let {x₀, x₁, x₂, x₃} be a coordinate system with the origin at the point O, related to the mutual tetrad. In a combined consideration of the coordinates {xⁱ} and {x_j} it is conventional to call the former contravariant coordinates and the latter covariant ones. From Eqs. (2.11) it immediately follows that in this case the coordinate axes of the contra- and covariant systems of coordinates coincide, while the coordinates themselves are connected by the relations

(2.12)

An arbitrary vector of Minkowski space is written in the tetrads under consideration as follows:

(2.13)

where the unit vectors and ^j are connected by the relations (2.11), and the components (coordinates) xⁱ and x_j of the vector satisfy (2.12); besides, here the conventional summing rule over repeated upper and lower indices has been used (sum from 0 to 3).

Any two-valent affine tensor over the space associated with Minkowski space can be represented in the following forms in the four tensor bases compiled from pair tensor products of the above tetrads vectors:

, (2.14)

where tensor product of vectors is denoted without a sign of multiplication between them.

The metric form (metric tensor) g in these four tensor bases can be represented

(2.15)

where the components of the tensor g in the bases under consideration are

(2.16)

From Eqs. (2.15), (2.16) it is seen that the component matrices of the tensor g are diagonal in all the bases used:

(2.17)

Let us prove the expressions (2.15) and (2.16). Substitute the quantities , and g=g^kl into Eq.(2.2). Using the relations (2.10), we find:

,

With the aid of the components of the metric tensor g one can carry out the so-called “index juggling”, i.e., transform the unit vectors of the starting and dual tetrads into each other, as well as the components of vectors and tensors referring to different bases:

(2.18)

Proof. Let us decompose the vector in the unit vectors of the dual tetrad: =e_ik. Multiplying scalarly on both sides of this equality by the unit vector _j and allowing for the relations (2.10) and (2.16), we find: e_ij=g_ij. Substitution of these e_ij into the above expansion of the vector _i leads to the first equality from (2.18). The second one is proved similarly. The remaining equalities are easily derived from the first two and the expressions (2.13) and (2.14). For instance, based on (2.14) and the second equality from (2.18), we have: T^ij_ij=^k_j=g^ki_ij, whence it follows T^ij=g^ki.

Each two-valent affine tensor T may be represented as a linear operator acting on the vectors either from the left: T()=TЧ , or from the right: T()=Ч T (generally TЧ № Ч T). In the matrix representation of vectors and linear operators a column matrix or a line matrix (xⁱ) is assigned to each vector . A tensor T corresponds to a square matrix of its components: either (), if T is acting on from the left, ((TЧ )ⁱ)=()(x^j), or (), if it is acting from the right, ((Ч T)^j)=(xⁱ)() (here is the notation for matrix multiplication). The trace and the determinant of these matrices are called trace and determinant of the tensor T:

(2.19)

The first relation from (2.19) follows from here as a consequence. Note that SpT№ Sp(T^ij)=Sp(T_ij) (the equality Sp(T^ij)=Sp(T_ij) is proved by (2.17) and (2.18)). The determinant detT of a tensor T may be defined in a similar way, irrespective of a coordinate system choice, although it would look somewhat bulky, and then the second relation from (2.19) could be derived.

According to expressions (2.17) and (2.19), the traces and determinants of the metric tensor g and the tensor - g, setting the identity transformation (2.7) and the inversion (2.8), respectively, are

(2.20)

In special relativity it is conventional to measure coordinates in Minkowski space in the units of length. The traditional units: a second, a minute, an hour, etc., are used in time measurements as well. Therefore the time coordinate x⁰ is expressed in terms of time using a positive constant factor c with the dimension of velocity:

x⁰ = ct . (2.21)

Let us indicate the physical meaning of the coefficient c. To this aim consider an object whose world line is a null straight line. Let be its radius vector. Let us present in the form

(2.22)

where is the temporal component of the radius vector and =x¹+x²+x³ is its spatial component. The radius vectors for two close points of the object world line are and (where d=dx¹+dx²+dx³). The scalar square of the vector connecting these points, (+d)- = d (= cdt+d), is zero:

(2.23)

by the properties of a null straight line, with allowance for (2.9). Based on (2.9), we have as well:

(2.24)

where it is denoted: dr =; dr і  0. The quantity dr is evidently the distance between the points of the three-dimensional space at which the object under consideration is located at the instants t and t+dt. Substituting the value from (2.24) into (2.23), we obtain

(2.25)

where it is denoted v =п dr/dtп and assumed that dt №  0. It is easy to see that the quantity v is the velocity magnitude of the above object. From expression (2.25) it follows that c=v. Hence the factor c in Eq. (2.21) is equal to the velocity magnitude of the object whose world line is a null straight line. As known, among these objects are photons and other zero mass particles (as they move in vacuum). Thus, the physical meaning of the quantity c is to describe the velocity of photons and other massless particles, in this connection it is conventionally called the velocity of light in vacuo.

The substantial conception of time, underlying the subsequent constructions, has a long history. Along with the substantial conception of space, it dates back to Democritus’ ideas ascribing a special kind of being a empty space. This conception has been most fully embodied in the Newtonian notion of absolute time. According to I.Newton, absolute time and absolute space are self-sufficient entities, independent both of each other and of material objects contained and processes occurring in them. It could be said that the Newtonian ideas of time have completed the formation stage of the substantial conception of time.

The further important step in the development of the substantial conception of time was made by N.A.Kozyrev (Kozyrev 1991). In his book “Causal or asymmetric mechanics in linear approximation”, published in 1958, N.A.Kozyrev formulated a number of axioms endowing time with properties in addition to duration, due to which time interacts with different physical objects and processes. He called these properties of time physical or active.

Unfortunately, N.A.Kozyrev did not provide a rigorous mathematical formulation of the notion of time substance in his papers. It should be noted that he did not use the term “substance” with respect to time at all and spoke less certainly about time as a “phenomenon of nature” which through its “active properties” may affect the course of events. The absence of a clear definition of time substance is a feature of other publications dedicated to the substantial concept of time as well. Besides, these publications neglect the fundamental difference between the time substance and any other physical field and matter. Namely, the time substance, if it exists, is necessarily an object of the fourth dimension, orthogonal to the three-dimensional space embracing matter and fields. Just this conclusion concerning the properties of the time substance undoubtedly follows from relativity.

Allowing for the aforesaid, we shall construct the theory on the basis of the following approach. Let us combine the substantial conception of time and the fundamental premise of modern physics that space and time form a single manifold. For simplicity we restrict ourselves to the case studied by special relativity when the above manifold is the four-dimensional real pseudo-Euclidean space of signature (1, 3), i.e., Minkowski space (see Section 2). Thus we adopt the following postulate.

Postulate I. Space and time form a unified four-dimensional substance; it is endowed with Minkowski space geometry and possesses certain physical properties due to which it interacts with matter, physical fields and processes occurring in it.

We call the postulated object space-time substance and denote it by S.

Since physics is a science of three-dimensional bodies, it is reasonable to introduce a notion unifying all the three-dimensional material objects, i.e. matter and physical fields. This unification is conventionally called physical space. For short, we shall call it our World. Let us define this notion more precisely.

Let us fix an orthogonal coordinate frame in the space-time substance S. We define our World M at an instant t (in accord with the ideas of special relativity) as the three-dimensional hyperplane of simultaneous events orthogonal to the time axis t and crossing it at the point with the coordinate ct, where c is the velocity of light in vacuum (Fig.2). The World M consists of matter and physical fields in the states corresponding to the given instant t. Note that due to a specific nature of pseudo-Euclidean geometry the hyperplane M, the time axis t and the instant t, generally, differ in different coordinate frames. We call the set of the World M and the space-time substance S the physical space-time. This notion incorporates all the material objects, i.e., matter, fields and the space-time substance available in the model being proposed.

The hyperplane of our World M occupies different positions in the space-time substance at different instants displaced with respect to one another along the time axis. A transformation of a space, preserving geometrical properties of figures, is called a motion (Motion, 1979). Therefore one can say that the World hyperplane moves through the space-time substance along the time axis. As it has been noted in Section 2, for each physical object of our World a world line orientation indicating the direction of its time evolution is objectively specified, so that orientations referring to different objects are concordant with each other. This experimental fact indicates that a definite direction may be ascribed to the World motion along the time axis. We call the domain of the substance S, from where the World is moving, the past, and the domain, to where it is moving, the future. The current state of the World being considered, is its present.

Let us introduce a vector , parallel to the time axis, directed from the past to the future and having a magnitude equal to c; we shall call it time direction (see Fig.2). The vector has the meaning of the World motion “velocity” through the substance S because it indicates the direction of that motion and its magnitude п п (= c) may be represented as a ratio of the “path” з cdtп passed by the hyperplane M along the time axis t for an interval dt to the absolute value п dtп of the same interval. The terms “velocity” and “path” are put in quotes to mark the relative character of their usage describing a motion along the time axis. The vector is the “velocity” of the World as a whole; as applied to specific physical objects existing in M and moving in it, appears to be the time component of their “velocities” with respect to the substance S. It should be emphasized that the directions of the vector are mutually consistent in all coordinate frames due to the above self-concordance of the world lines orientations of all physical objects (the vector itself, as well as the time axis t and the hyperplane M, may differ in different coordinate frames). Evidently the vector, which we have called time direction, is related to the unit vector of the time axis by the equality

(3.1)

where the plus sign is taken in the case of the vector directed from the past to the future, and the minus sign if otherwise.

By the aforesaid our World M moves through the space-time substance S from the past to the future with the “velocity” . At the same time for an observer inseparably linked with M, this motion looks as if the substance S flowed through our World from the future to the past with the “velocity” -. Thus the time direction is an objectively distinguished characteristic describing the relative motion of two physical realities: our World and the space-time substance.

Let us make a remark concerning the model under consideration. The notion of interaction of the space-time substance with our World is essential for this model. It is unlikely that objects having strictly different geometric dimensionalities would be able to interact with each other (e.g., a zero thick wall could be hardly felt as a barrier). Our World has apparently a certain thickness along the time axis. The thickness is probably very small, otherwise that fact would not have passed unnoticed by the researchers. The idea of nonzero thickness of the World admits two different interpretations. It could be understood as a certain fixed, determined characteristic of the World, or one might treat it in the spirit of quantum-mechanical ideas as a microscopic “uncertainty” or “smearing” of the World along the time axis reflecting an uncertainty in the values of time coordinates of the events of the World. If the World has indeed a nonzero thickness along the time axis, then its modelling by a hyperplane should be regarded as an idealization or the first approximation. Thereby in the cases when just the zero thickness of M is of importance, e.g., when using reflections in M (see below), one should understand the symbol M as indicating the middle hyperplane of the World.

In the subsequent sections the consequences of Postulate I will be analysed, including the possible observable effects of our World due to the action of the space-time substance on it. Definitions and postulates, developing the model, are also introduced.

Having adopted Postulate I on the existence of the space-time substance, one can assign a clear physical sense to the general scientific concepts of the time flow and time direction. Indeed, it has been noted that from the standpoint of an observer linked to our World M the World motion through the space-time substance S looks like a stream of the substance S through our World from the future to the past with the “velocity” -. The fact that the substance S crosses the World in a direction parallel to the time axis allows one to speak of it as of a “time flow” penetrating our World. In this connection the following meaning can be assigned to the notions of time flow and its direction.

The time flow is the World motion through the space-time substance as perceived from inside the World. (The mechanism of this perception may be presented in detail after specifying the physical properties of the substance.) Time direction is a notion reflecting the fact that the direction of the above motion is fixed in each orthogonal coordinate frame in Minkowski space. This direction is set by the vector , and that was the reason for calling it time direction. Figuratively speaking, our World is an ark sailing across the space-time ocean and time direction is the vector specifying motion direction and velocity.

Since the space-time substance S is perceived from inside the World as a “time flow”, it is reasonable to call it the time substance. In what follows we shall use for the substance S this shorter term as well.

Note that the relational outlook of time does not allow one to treat the time flow and its direction in a way similar to that presented above. It is also impossible to introduce a characteristic similar to the vector . The point is that in the framework of the relational conception of time there is no reference body, independent of M, in whose respect the World motion from the past to the future could be considered. Such a motion would be no more than a mental picture, not physical reality.

Modern physics is known to make only numerous unsuccessful attempts to realize the idea of time direction (Landau and Lifshitz 1976, Section 8; Penrose 1979; Reichenbach 1956, etc.) in spite of the seeming easiness. Therefore such divisions of physics as classical mechanics, relativity theory, quantum mechanics and statistical physics deal with time having no objectively distinguished direction. The results of the present investigation allow one to conclude that the present-day absence of a rigorous definition of time direction in physics is most likely caused by the fact that modern physics is based on the relational conception of time.

Let us compare the methods of specifying coordinate systems in special relativity and in classical mechanics.

Classical mechanics describes motions of bodies in the three-dimensional space, therefore the coordinate systems used in it generally comprise three spatial coordinates. As motions of material bodies are always studied with respect to other bodies, each coordinate system is related to a certain material body, the reference body. More precisely, a coordinate system is introduced in such a way that a certain point of the reference body (e.g., its center of mass) has fixed values of coordinates remaining unchanged in the process under study. The coordinate system is as though “attached” to the reference body at this point. Moreover, in many cases a coordinate system is “attached” to the whole reference body.

The situation is different in special relativity. Here body motions are considered in the four-dimensional space-time manifold and therefore coordinate systems incorporate the fourth, temporal coordinate in addition to the spatial ones. In this case the spatial coordinates, as well as in classical mechanics, are connected with a certain reference body while the values of the fourth coordinate are determined from readings of clocks at rest with respect to the reference body. The fact that the clocks are assumed to go permanently means that their temporal coordinate, which serves as a temporal coordinate for the reference body as well, is a variable quantity. Hence the reference body, although it looks as being at rest with respect to the given coordinate system, essentially has only three spatial coordinates fixed, whereas for the temporal one this is not the case (Fig.3). That means that coordinate systems introduced in Minkowski space are not “attached” to any body, being as though suspended in (four-dimensional) vacuum. Thus the method of specifying coordinate systems in special relativity does not correspond to that adopted in mechanics.

The reason for the above disadvantage is the fact that relativity uses the relational conception of time, assuming that there are no material objects other than matter and physical fields. If, in accordance with Postulate I, one assumes that along with these objects there is a material medium of a specific kind, i.e. the time substance S, then the above disadvantage vanishes, since just this substance serves as the reference body to which the coordinate systems of relativity are “attached”. (This “attachment” occurs since the coordinate systems used in special relativity are introduced in our model from the outset as those fixed with respect to the substance S.) Thus Postulate I enables one to reconcile one of the basic constructions of relativity with the general principles of mechanics.

The presence of the time substance and the motion of our World through it make the two sides of the World hyperplane M inequivalent: one of them is faced against the “time flow”, the other follows it. Assume that in our World there are objects nonsymmetric with respect to reflection in the hyperplane M. Such objects can be described mathematically by vectors orthogonal to the World hyperplane. Let an object specified by the vector /п п directed against the “time flow” be named a “particle” (in quotes), and an object specified by the vector -/п п of the opposite direction be named an “antiparticle”. We shall consider the “particle” and “antiparticle” to be corresponding to each other if they are described by the vectors /п п and -/п п having the same coefficient a (Fig.4).

Fig.4. A cross section of the World M crossing a “particle” and its corresponding “antiparticle”: =/ï ï is the unit vector orthogonal to the hyperplane M and having the same direction as.

Here a > 0 and b > 0; the physical dimension of the values a and b is not specified since it does not matter for what follows; /п п is the unit vector directed as ; it is assumed that № . Recalling what has been said about vector lengths in Section 2, note that the usage of the length п п is of no importance here since a unit vector like /п п can always be defined without referring to п п .

“Particles” and “antiparticles” can be hypothetically exemplified by the objects shown in Fig.5a for a World of zero thickness along the time axis and by the ones shown in Fig.5b for a World of nonzero thickness. (Figure 5 is purely illustrative since the objects depicted in it are not meant to be compared with any real physical bodies; the only purpose of the figure is to demonstrate that the required objects can exist at least from the standpoint of geometry.)

It is natural to expect that an interaction of these objects with the time substance S, if it exists, be described by a quantity incorporating scalar product of the time direction vector and a vector specifying the object (see Fig.4). For a “particle” and the corresponding “antiparticle” the above scalar product is equal to

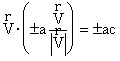, (6.1)

where it is taken into account that ; the plus and minus signs correspond to a “particle” and an “antiparticle”, respectively. It follows from (6.1) that a “particle” and its corresponding “antiparticle” interact in different ways with the substance flow S running on one side of the World. This fact may be perceived from inside the World as a difference in some properties of the above objects. Thus, one of the observable effects in our World caused by the existence of the time substance can be a difference between the properties of “particles” and their “antiparticles”.

Let us reverse the direction of World motion along the time axis, i.e. change the sign of the time direction. From the definition of “particle” and “antiparticle” and from Figs. 4 and 5 it can be seen that “particles” are thereby converted to “antiparticles” or vice versa. At the same time from inside the World this transformation will be perceived differently depending on the way of identification of the above objects. Two different cases are possible here. One consists of the “particles” and “antiparticles” being identified by their properties determined only by the World internal characteristics. To put it clearer, one can imagine a certain object to be just gripped in his hand (i.e., identified by its unchangeable geometric and mechanical properties). Then we will of course believe that before and after changing the sign of we have one and the same object. Even its comparison with similar objects would not suggest that it has been converted into something different, as all similar objects change in a similar way. Hence in this case the result of the above transformation will be perceived from inside the World as a mutual change of some properties of “particles” and “antiparticles” (namely, those caused by their interaction with the substance S). The situation is different when objects are identified by just the properties determined by their interaction with the time substance S. Then the result of this transformation will be perceived from inside the World as a real interconversion of “particles” and “antiparticles”.

From the viewpoint of an observer situated inside our World, the sign change looks like a reversion of the time flow direction, therefore in all physical theories the temporal variable t should be replaced by -t. Hence, it is quite possible that among the pairs of physical systems whose certain characteristics, or even the equations describing them, are entirely converted into one another when the t sign is changed, there are just the “particle” — “antiparticle” pairs, having different properties just due to the action of the time substance.

From the definition of these objects and the aforesaid it follows that a “particle” and its corresponding “antiparticle” may annihilate when combined (since their vectors /п п and -/п п add up to zero) and that an “antiparticle” is a “particle” moving back in time. Real particles and antiparticles are known to possess these properties, hence one may assume that the “particles” and “antiparticles” we have introduced here coincide with the corresponding real objects. It is clear, however, that this conclusion cannot be considered to be unconditionally true only on the basis of these arguments. Hence we state it in the form of a suggestion and put the names of the introduced objects in quotes.

Note that from the standpoint of the relational conception of time the existence of objects described by vectors orthogonal to the World M seems unlikely. According to this conception, there are no material bodies outside our World which would interact with it, therefore all the properties of World objects should be determined only by its internal geometry. Since from the viewpoint of internal geometry of a hyperplane its two sides are equivalent, the presence of objects distinguishing one of the World sides would be beyond the scope of its internal geometry. Even if objects similar to a “particle” and the corresponding “antiparticle” appeared in our World, they would be quite indistinguishable from one another because they would interact identically with all the other objects of our World (the latter being symmetric with respect to a reflection in M). Here, however, we should make a reservation. If the World is not flat, its two sides turn out to be inequivalent to each other. For example, if the World forms a three-dimensional hypersphere, then one of its sides is faced in the convexity direction, while the other in the concavity direction. In this case objects described by oppositely directed vectors orthogonal to the World hypersurface (if such objects existed) could, in principle, possess different properties.

Let us present some definitions corresponding to real Euclidean spaces of any finite dimension.

Two geometric figures are said to be equal (identical, coincident) if they can be made coinciding by continuous motion in the space under consideration. Two physical systems are said to be equal (identical, coincident) if the mathematical constructions describing them are equal as geometric figures. A figure or system being an image of the initial one in a reflection in a hyperplane is its mirror reflection (the formula describing the transformation of reflection in a hyperplane are omitted as it is evident). A geometric figure or physical system having a hyperplane of symmetry is called mirror symmetric. If a figure (a system) has no hyperplane of symmetry, it is called mirror asymmetric. A mirror asymmetric physical system is sometimes called dissymmetrical or chiral.

As applied to a physical system, these definitions may take into account not only geometric but also mechanical or other system characteristics. It is clear that the referring of a real physical system to the class of mirror symmetric systems or to that of mirror asymmetric ones may depend on the set of its characteristics to be taken into account and on the accuracy up to which the system and its mirror reflection are compared.

A mirror asymmetric geometric figure (physical system) and its mirror reflection are not equal to each other. This fact allows one to introduce the concept of enantiomorphism. This term denotes the phenomenon of existence of pairs of mirror asymmetric figures (physical systems) each of which is equal to the mirror reflection of the other. Two such figures or systems are called (mutually) enantiomorphous; each of them is thereby said to be an enantiomorphous modification of the other. Allowing for the latter term, a mirror asymmetric figure or system can be called a figure (system) being in a certain enantimorphous modification. As applied to physical systems, the term “enantimorphism” is interchangeably used with the terms “dissymmetry” and “chirality”.

Let us pay attention to the fact that the concept of enantiomorphism is essentially based on the condition by which a motion mentioned in the definition of figure equality occurs within the space under consideration. Indeed, if an exit into the embracing space were admitted, then at least in the case of proper Euclidean space any figure and its mirror reflection could be superposed by a continuous motion. As a result, the figure and its mirror reflection would be equal and the concept of enantiomorphism would have lost any meaning. For example, on a proper Euclidean plane two identical circumferences with fixed mutually opposite round-trip directions are known to be enantiomorphous and cannot be transformed to one another by a continuous motion within the plane. However, if one assumes the possibility of an exit into the embracing three-dimensional proper Euclidean space, they can be superposed. To that end it is sufficient to turn one of them by 180° with respect to the plane under consideration about any axis lying in it, after that the coincidence of the circumferences can be achieved just by a continuous motion within the plane (Fig.6). In a similar way the mutually enantiomorphous right- and left-screw spirals in our three-dimensional World, unable to be coincided inside the World itself, could be transformed to one another if there were a possibility of their displacement into an embracing four-dimensional proper Euclidean space.

The bases of Euclidean space constitute an important example of mirror asymmetric geometric figures. Due to mirror asymmetry of bases the whole set of them can be divided into two unoverlapping classes, the right- and left-oriented bases, with the bases of each class being connected with each other positively in a certain sense. Being reflecting in a hyperplane, the bases of the two classes transform into one another. Sometimes these bases are more concisely called right and left ones.

Right- and left-oriented bases may always be put into correspondence to a pair of enantiomorphous figures or systems. A geometric figure (physical system) to which a basis of a certain orientation has been put into correspondence is called oriented. It should be emphasized that only a mirror asymmetric figure (system) can be oriented. A correspondence of a basis of a certain orientation to a figure (system) automatically implies correspondence to the latter of the whole class of equally oriented bases. We shall subdivide the oriented figures and systems into right and left ones in accordance with the orientation of bases put into correspondence to them.

The notion of orientation is used in mathematics with respect to the whole space as well. To orient a space means to choose in it one of the two classes of bases specified by the criterion of being right or left. An orientation of space may be introduced either by a direct choice of the class of bases, or by setting a mirror asymmetric geometric figure, i.e., by putting into correspondence the classes of oppositely oriented bases to the figure and to its enantiomorphous modification by a certain rule.

The World as a whole is said to be mirror symmetric if, first, all the mirror asymmetric physical systems and their enantiomorphous modifications are represented in it in equal quantities and, second, any two mutually enantiomorphous systems possess the same properties (more precisely, all the properties of one system transform into those of the other by mirror reflection). Otherwise the World is considered to be mirror asymmetric.

Let us return to the consideration of our model.

Since the concept of a mirror asymmetric physical system and that of an oriented system are applicable to spaces of any finite dimension, we shall apply them not only to three-dimensional objects of our World, but also to the four-dimensional time substance S. Let us adopt the following postulate.

Postulate II. The physical properties of the space-time substance S are such that make it mirror asymmetric; this property is of local nature, i.e. each arbitrarily small domain of the substance is mirror asymmetric.

Note that if the substance actually possesses mirror symmetry, the adoption of Postulate II does not lead to a large error, since the theory can always be reduced to this case by tending all the parameters characterizing the difference between two enantiomorphous modifications of the substance S to zero. The locality condition is adopted here to be able to extend the conclusions concerning action of the time substance on our World to most various physical objects, including the ones simulated by material points.

The time direction objectively singles out one of the two normal directions to our World hyperplane M allowing to introduce in our World an orientation induced from the embracing substance S.

The following method is adopted in mathematics to introduce an induced orientation in a hyperplane when a singled out normal to it has been set. One takes a basis from the hyperplane and adds the normal singled out to its constituent vectors. This normal is adopted as the first one from the obtained set of vectors, while the other vectors are numerated in the same order which they had in the initial basis. This set of vectors forms a basis of the embracing space. If this basis is right (left) in the embracing space, then the initial basis of the hyperplane is also considered to be right (left). An induced orientation of the hyperplane is fixed by chosen in it a class of bases named like that chosen in the embracing space.

The hyperplane orientation introduced in such a way is evidently not a physical reality but just a mathematical construction. At the same time, due to mirror asymmetry of the time substance S and its interaction with our World, an induced orientation of the World may really become physical reality. Let us show that it is indeed the case.

Let us set an orientation of the substance S by assigning to it a class of equally oriented tetrads (which can be done due to the postulated mirror asymmetry of S). Let {} be an orthonormal basis (tetrad) of this class (the unit vectors , i=0,1,2,3, satisfy relations of the type (2.9)). Let us form the alternated tensor product, the polyvector

(7.1)

of the vectors of the above tetrad, where the square brackets mean alternation; the tensor product is written without a multiplication sign between the multipliers. The quantity x is an invariant characteristic of substance S orientation, since, as is known (Rashevsky 1967), a polyvector formed from an orthonormal system of vectors does not change when this system is replaced by any other systems of orthonormal vectors of the same orientation and changes its sign when it is replaced by an oppositely oriented system of orthonormal vectors.

Let us consider two enantiomorphous physical systems from M. We orient them by putting them into correspondence orthonormal bases (triads) in M: a right triad {} to one of them and a left triad {,,} to the other (the vectors _i and , i = 1,2,3, are imaginary-unit ones). We shall call these systems right and left ones, respectively. From the viewpoint of internal geometry of the three-dimensional World M the orientations of these systems is characterized invariantly by the polyvectors [] and []. From the standpoint of the substance S embracing the World M, the four-valent tensors

(7.2)

can be used as characteristics of these systems reflecting both their orientations and their motion along with M with respect to the substance S, where (recall) /п п is a unit vector orthogonal to M and directed in the same way as . Due to the above property of polyvectors we have [] = - [], hence

(7.3)

It is natural to assume that interaction of the mirror asymmetric time substance S with these right and left systems, if it occurs, is described by a quantity containing the product x...y for one class of systems and x...yў for the other (dots denote the operation of tensor contraction over all four pairs of indices). Let us prove that

x....y = -x....yў = m 1/4! , (7.4)

where the upper and lower signs correspond to the cases when the ordered tetrad {/п п , ₁,₂,₃} has the same and opposite orientation as the tetrad {}, respectively.

, (7.5)

Both multipliers being contracted in the right side of this expression may be represented, by definition of a polyvector, as sums of n! terms (n=4 for the first factor and n=3 for the second one). Each summand in both sums is a tensor product of the four vectors /п п , , , taken for each term in its own order; the summands are endowed with definite signs and the whole sum is multiplied by 1/n!. As the vectors are orthogonal in pairs, nonzero contributions to the contraction of sums are given only by those summands where contraction comprises scalar products of the same vectors by themselves. Since these summands have the same signs and (/п п )Ч (/п п ) = 1, Ч =Ч =Ч = -1, each contribution is equal to -1. The total number of these contributions is 3!, hence the sum is -3! in total. Multiplying this number by the coefficient ± 1/(4!3!) and taking into account Eq.(7.3), we obtain the required relation (7.4).

From Eq. (7.4) it follows that the time substance S interacts in different ways with right and left systems of our World. From inside the World it can be perceived as a difference in the properties of these systems. Hence, as has been stated above, the World orientation, induced from the time substance embracing it, may indeed be an objective physical reality able to manifest itself in the form of mirror asymmetry of the World.

Apart from the above proof, let us confirm this conclusion by the following clear example.

Let us take a narrow metallic band and twist it about its central axis to form a screw spiral. Let us also take a plate with a rectangular hole in the middle, coinciding in shape with the band cross-section. Insert an end of the band into the hole and pull it through the plate, as shown in Fig.7. As this was done, the plate will rotate (the directions of band motion and plate rotation are shown in the figure by the arrows for the case of the band being a right twisted spiral). An orientation in three-dimensional space is known to be fixed by a choice of a certain twisting direction of a screw spiral, while on the plane it is fixed by setting up the direction of rotation. In our example there is a tough dependence between the direction of band motion and that of plate rotation. However, we cannot yet say that this band twisting induces a certain plate orientation because if the band is pulled in the opposite direction, the plate will rotate otherwise as well.

Now let us make the two opposite directions of band pulling inequivalent. To do that we may place a special device in the middle of the plate: the latter should leave unchanged the described picture of band motion in one direction, while when it moves back, the width of the hole increases to the size of the band width, allowing the band to pass easily through the plate without causing any rotation of the latter (it is simply realizable technically, e.g., a humming-top contains a device like that). In this case the band motion will lead to plate rotation only in a strictly fixed direction. Thus, singling out the direction of a normal to the plate, we obtain a one-to-one connection between the orientation of the spiral and that of the plate.

The above example supports the conclusion that if a normal direction to a subspace is singled out physically, the action on material structures of the subspace exerted by mirror asymmetric structures of the embracing space may induce in that subspace a difference between the properties of right and left systems.

Let us change the sign of the time direction . Thereby the induced World orientation will become opposite: right systems will be converted into left ones and vice versa. At the same time, we, who are living inside the World, divide the systems into right and left ones in accordance with only internal geometry of the World, irrespective of geometry of the substance S. Therefore for us the change of the World orientation induced from S will look like a mutual change of that properties of right and left systems which occurs due to the action of the time substance. It has been noted above that, when the sign of is changed, the time variable t in all physical theories should be replaced by - t. Consequently, if the replacement of t by - t transforms the properties of certain physical systems into those of their enantiomorphous modifications, then it is not excluded that these properties are caused just by the action of the mirror asymmetric time substance. Note that a pair of enantiomorphous systems may be simultaneously a “particle” — “antiparticle” pair since the latter mutually change their properties when the sign of t changes as well.

Examples of observable mirror asymmetry are found in spatial parity violations in beta decays of atomic nuclei and in a number of atomic phenomena (Khriplovich 1988); one more example is the asymmetry of planetary figures with respect to reflection in the equatorial plane (Katterfeld and Galibina 1988; Kozyrev 1991) (in the latter case a screw combination is formed by the gravity force vector and the angular velocity pseudovector of the planet proper rotation; for the usual direction of planet rotation from the West to the East this screw is left for the Northern hemisphere of the planet and right for the Southern one). There are numerous manifestations of mirror asymmetry in living matter, which is most brightly expressed in the fact that the twisting of nucleic acid molecules is exclusively right, while that of proteins is exclusively left (Kizel’ 1985). This property of living matter, first studied by L.Pasteur, is considered by some scientists to be one of the basic indications of life (Vernadsky 1988, etc.).

By now no satisfactory explanation has been found for the effects of mirror asymmetry of the World, in spite of numerous attempts made in this field. The failure is probably related to the fact that all these attempts have been based on the theories using the relational conception of time. In the framework of those theories any physical phenomena should be explained only on the basis of the properties of the World itself. From the viewpoint of hyperplane internal geometry one cannot find a cause able to induce a difference in the properties of right and left systems. On the contrary, the use of the substantial conception of time, as follows from the results of the present section, gives an opportunity to resolve the problem of the origin of World mirror asymmetry.

Thus, by the results of the present and previous sections, the presence of the time substance, the unidirectionality of the World motion through it (as specified by the vector ) and an interaction between the World and the substance may lead to a difference in the properties of “particles” and “antiparticles” in the World; in addition, if the time substance is mirror asymmetric, a difference between right and left systems can be obtained. It is commonly assumed that a comparison of the World states referring to different instants is necessary to reveal the effects related to time. The result presented here shows that it is not the case. Some effects may be, figuratively speaking, imprinted even on an instantaneous photograph of the World.

N.A.Kozyrev was the first to put forward the hypothesis that the mirror asymmetry of the World is caused by the properties of time (Kozyrev 1991, pp.232-287).

Special relativity postulates that physical processes occur in the same way in any inertial frame of reference. This means, in particular, that if an arbitrary physical system is transformed from one uniform rectilinear motion (with respect to a certain inertial frame of reference) to another motion of the same kind, then all processes unrelated to external systems will proceed exactly in the same way as they did in the initial state. Consequently, these transformations of physical reality are its symmetry elements (which include, in particular, arbitrary turnings and transitions). Orthogonal coordinate systems correspond to inertial frames of reference in Minkowski space, while transformations of Minkowski space transferring one orthogonal coordinate system to another correspond to the above symmetry elements. It is of importance that these coordinate system transformations conserve the concordance of time axes directions and space axes orientations (their being right or left). The set of all such transformations forms one of the four connected components of the Poincarй group, the isometry group of Minkowski space. Characteristic of these transformations is that they can in principle be conducted in a continuous way.

We shall be interested in the symmetry properties of the described substantial space-time model under inversion transformations (being one of the types of discrete transformations of Minkowski space).

Let a transformation of the physical space-time be called a space-time inversion if it transfers all the points of the time substance S and our World M from the places where they are situated to the places symmetric to them with respect to a certain point of the World, called the centre of inversion, with simultaneous sign changes of all vector characteristics of the model, including reversion of the World motion through the substance S. We denote this transformation by the symbol W (without specifying the center of inversion and the instant when the transformation occurs). Various space-time inversions, considered as mappings of Minkowski space, together with the above continuous transformations form one more connected component of the Poincarй group. However, unlike the transformations mentioned above, they cannot be realized in a continuous way.

From Eqs. (2.8) it follows that a space-time inversion W transforms the Minkowski space vectors in the same way as the operator -g:

W = -g: a -g Ч = -, (8.1)

where g is the metric form of Minkowski space acting here as a linear operator; is an arbitrary vector of Minkowski space. Let be the radius vector of points of the time substance S or those of the World M, drawn from the center of inversion; be the time direction; /п п and -/п п be vectors specifying “particles” and “antiparticles”. By (8.1), an inversion W transforms these vectors by the rule

(8.2)

If the model has other vector characteristics, their signs should also be changed to the opposite ones; the same refers to the characteristics described by any odd rank tensors (because they can be represented in the form of linear combinations of tensor products of an odd number of vectors).

Furthermore the following transformations of the physical space-time are used along with the inversion W :

I, the identity transformation; it transforms the physical space-time into itself without any change in it (by (2.7), the transformation I coincides with the operator g on the set of Minkowski space vectors);

W _M, a restriction of the transformation W onto the hyperplane of our World M, i.e., a space-time inversion of the World with respect to one of its points (it consists of changing the signs of the radius vectors of World points and the signs of all the vectors and odd rank tensor characteristics of the World, including those having nonzero components along the time axis, in particular, it transforms all “particles” into the corresponding “antiparticles” and all “antiparticles” into the corresponding “particles”); it is realized with no change of the time substance S and the time direction;

W _S, a restriction of the transformation W to the time substance S, i.e. a space-time inversion of the substance S with respect to a certain point lying in the hyperplane of our World M; it leaves unchanged the World M and the time direction;

, sign change of the time direction , i.e., reversion of the World motion along the time axis;

P, spatial inversion, sign change of the radius vectors of all the World points, drawn from a certain point of the World; this transformation changes the orientations of physical objects in M: right objects become left ones and conversely; the transformation P differs from W _M in that it does not change any other characteristics of the World, in particular, it leaves “particles” and “antiparticles” unchanged (although displaces them in space);

C, charge conjugation, changing the signs of the vectors and , characterizing “particles” and “antiparticles”; it transforms all “particles” into the corresponding “antiparticles” and all “antiparticles” into the corresponding “particles”.

The latter two transformations, P and C, are contained in W _M .

If the World M has a nonzero thickness along the time axis, then the centers of all inversions should belong to the middle hyperplane of the World.

In Section 3 it was pointed out that the physical space-time concept incorporates all the material objects described by the model. Since this fact is essentially used in what follows, let us express it in the form of an independent postulate.

Postulate III. The physical space-time embraces the whole reality.

Now let us turn to a direct description of the symmetry of our model under inversions.

As it is easy to confirm, the physical space-time is transformed to itself if the following transformations are carried out:

perform a space-time inversion of the World M with respect to its certain point (the transformation W _M);

reverse the World motion along the time axis, i.e., change the sign of the time direction (the transformation );

perform a space-time inversion of the substance S with respect to the same point belonging to M (W _S);

perform an inversion of the whole physical space-time with respect to the same point (W ).

Consequently, we can write down:

(8.3)

Eq.(8.3) expresses the law of physical space-time symmetry under inversion transformations. Two requirements are of importance here: first, the inversions W , W _S and W _M should be carried out with respect to the same World point; second, all the transformations should be carried out at the same time instant. Let us formulate the conditions under which the first of these requirements could be removed. Let us previously prove a lemma.

Lemma 1. Let Q be an arbitrary domain of an affine space; O₁ and O₂ be any two points of the space; W ₁ and W ₂ be inversions with respect to the points O₁ and O₂. Then: (a) the images of the domain Q by the inversions, W ₁ and W ₂, differ only in their space locations, being displaced with respect to one another by the vector ;

(b) the image of the domain Q by the superposition W _{2W 1} differs from the domain Q itself only in its position in space: it is displaced with respect to Q by the same vector .

Proof. In the case of a one-dimensional affine space the validity of the lemma is evident. Assume that the space has a dimension no less than two. Choose an arbitrary point AО Q and consider the plane passing through the points A, O₁ and O₂ (Fig.8). Let us denote by A', A" and A'" the images of the point A by the inversions W ₁, W ₂ and their superposition W _{2W 1}, respectively. The points A' and A" lie in the above plane since they belong to the continuations of the segment AO₁ and AO₂ contained in it; the point A''' belongs to this plane as well because it is located on the continuation of the segment A'O₂. From Fig.8 it is seen that the segment O₁O₂ is a middle line of the triangles AA'A'' and AA'A'''. Hence , which proves the lemma due to the arbitrariness of the point A.

Let us apply Lemma 1 to the whole physical space-time. In so doing, we shall speak of its image and the images of M and S after inversions as of these objects themselves being in new states.

From Lemma 1 it follows that the states of the physical space-time after the inversion W performed with respect to different centers, differ only by its displacement (translation) as a whole by a certain vector. Since according to Postulate III there is no reference body with respect to which a displacement of the whole physical space-time could be determined, such as its states are physically indistinguishable. Therefore the symmetry law (8.3) is independent of the inversion center location used in the transformation W .

The situation is different for the inversions W _S and W _M. Being performed with respect to different centers, each of them leads to different mutual positions of the World M and the time substance S, which in principle may be detected. According to Lemma 1, these states of the World M and the substance S differ by the World’s displacements with respect to S along the World itself (since the centers of the inversions W _S and W _M lie in M). Hence, if among the symmetry elements of the substance S there are translations by an arbitrary vector parallel to M, in other words, if the substance S is homogeneous along each hyperplane of simultaneous events, then such states of the physical space-time are indistinguishable as well and the law (8.3) is valid irrespective of whether the centers of the inversions W _S and W _M coincide or not.

Thus, if the time substance S is homogeneous along each hyperplane parallel to our World M, then the requirement that the inversions incorporated in the physical space-time symmetry law (8.3) have a common center in M, may be removed. We would like to present one more condition which ensures the fulfillment of the law (8.3) irrespective of the above requirement being satisfied.

Let us consider the case when the time substance S is symmetric under an arbitrary inversion W _S with a center lying in M. This will be the case, e.g., if the properties of the substance S are characterized by homogeneous scalar fields (but not vector ones (!), since the transformation W _S changes the signs of vectors). Let us prove the following lemma.

Lemma 2. If the space-time substance S is symmetric under an arbitrary inversion W _S whose center lies in the hyperplane of our World M, then it is homogeneous along each hyperplane parallel to M.

Proof. Consider an arbitrary hyperplane M' parallel to the World M and choose any two points A and B in it, belonging to the time substance S. Let O₁ and O₂ be points of M satisfying the condition =(as M'║ M, such a pair of points exists and, moreover, is not unique). Denote by W _S1 and W _S2 the inversions of the time substance S with respect to the centers O₁ and O₂, respectively. Now let us act on the substance S by the superposition of inversions W _{S2W S1}. From Lemma 1 it follows that this procedure will result in displacing the substance S forward by the vector . Thereby the point A will be transferred into the point B of the initial state of the substance since =.

By the condition of the lemma being proved, the substance S is symmetric under the inversion W _S. Hence its state after the inversion W _S1 is indistinguishable from the initial one. Therefore the substance in the inverted state is symmetric under W _S2. This means that the superposition of inversions W _{S2W S1} is one of the symmetry elements of the substance S. As the transformation W _{S2W S1} transfers the point A into the point B, this symmetry implies that the properties of the substance S at the points A and B are identical. From arbitrariness of the positions of these points in M' it follows that the substance S is homogeneous along the whole hyperplane M'. The arbitrariness of M' in turn implies that the substance S is homogeneous along each hyperplane parallel to M, that is what we had to prove.

Note that the reverse of Lemma 2 is not true: the homogeneity of the time substance S indicated in Lemma 2 does not necessarily imply its W _S-symmetry. (Indeed, let the substance S be such that its physical properties are characterized by the same vector at all its points. Such a substance is homogeneous not only along the hyperplanes parallel to M but throughout the space-time. The inversion W _S is, however, not its symmetry element since it changes the characteristic , transforming it into .)

We have shown previously that if the substance S is homogeneous along each hyperplane parallel to the World M, then the symmetry law (8.3) is fulfilled irrespective of whether or not the centers of the inversions involved in this law coincide. This and Lemma2 lead to one more condition ensuring the validity of the law (8.3) for arbitrary centers of the inversions involved. This condition consists of the symmetry of the time substance S under any inversion W _S with a center in M.

Let us describe some properties of the transformations of interest.

Lemma 3.

, (8.4)

Proof. From Lemma 1 it follows that the physical space-time, being subject to a superposition of two space-time inversions W having a common center in M and realized at the same time instant, transforms into itself. This means that W W = I. Hence follows the equality W ^-1 = W . Similar equalities are valid for the transformations W _M, W _S and as well, therefore the first four equalities from (8.4) are true. From the symmetry law (8.3) it follows that W ^-1 = W _SW _M. Hence, allowing for the relation W ^-1 = W , we obtain the last equality from (8.4), which completes the proof.

The last equality from (8.4) may be treated as a decomposition of a space-time inversion W into component operations: an inversion of the World M, sign reversion of the time direction and an inversion of the time substance S.

We would like to present arguments in favor of regarding the space-time inversion W as a symmetry element of the physical space-time.

The transformation W possesses the following properties. First, it is a Minkowski space isometry, i.e., conserves the scalar products of vectors; second, it conserves the orientation of the substance S, which follows from the transformation determinant being positive: detW = det(-g) = 1 (see Eqs. (2.20), (8.1) and the definition of the concept of orientation identity (Rashevsky 1967, p.142)); third, it transforms our World hyperplane into itself (since the inversion center lies in it); finally, it transforms all the light cones into light cones (which immediately follows from Eqs. (2.6) and (8.2)). Hence it is seen that the transformation W leaves the basic geometric characteristics of the physical space-time unchanged.

Now let us pay attention to the following circumstance. We always judge a change of parameters of any physical system from the results of their measurements by certain instruments considered to be invariable, more simply, by confronting them to the corresponding primary standards. However, if a standard itself is a part of the system under study and changes together with it, a change which has happened cannot be detected with its aid. The transformation W realizes just this case. All standards available are part of the physical space-time and change along with it. This change proceeds in such a way that the standards serving to measure the same physical quantity change identically (the latter follows from the fact that each standard is defined ultimately by mutual arrangement of some physical objects in space and time, while the transformation W , as follows from its properties indicated above, conserves the mutual arrangement of all the points of the physical space-time). In this connection, as the symmetry properties of the physical space-time are studied from inside our World, it is impossible to detect changes induced by the transformation W . Therefore, as it has been stated above, there is good reason to believe that the inversion W should be regarded as one of the symmetry elements of the physical space-time.

It should be noted that the above consideration implicitly uses Postulate III claiming that the physical space-time embraces the whole reality. Indeed, if a certain entity interacting with our World but not belonging to the physical space-time existed, we would be able, if only in principle, to detect changes induced by the transformation W by comparing the parameters of the World and that entity. It could be possible, for instance, if the above entity were characterized by spatial inhomogeneity. In such a case we would have a frame of reference independent of the physical space-time and could have fixed that, as a result of the transformation W , some objects of our World were displaced with respect to the above frame of reference to the locations where these objects had been absent in the initial state. That alone would be evidently sufficient for asserting that W should not be included among the symmetry elements of the physical space-time. However, since such an independent entity is not observed in experiment, we are unable to detect changes induced by the transformation W .

Thus, there is good reason to believe that the symmetry group of the physical space-time as determined from inside the world M, contains the space-time inversions W .

From this conclusion it follows that, as long as the symmetry of the physical space-time is studied from inside our World, the law (8.3) appears for us in the reduced form

(8.5)

In the particular case of an W _S-symmetric substance S the same law will take the form

(8.6)

We emphasize that the symmetry laws (8.5) and (8.6) reflect not only the objective properties of nature but also the peculiarities of our perception of them from inside our World. Therefore these laws may be used only with a reservation that they describe the physical space-time symmetry from inside our World. Eq.(8.3) and the last equality from (8.4) give an exact mathematical dependence between the operators involved in these laws.

The transformation W _M converts the right objects of our World into left ones, “particles” into “antiparticles” and vice versa. At the same time, from the inside of the World it is impossible to detect these transformations, because all the primary standards, by comparison with which we might judge of objects being right or left and of their belonging to “particles” or “antiparticles”, change simultaneously and similarly with the objects themselves. For this reason the result of the transformation W _M would not be perceived from inside the World as a transformation of those objects into one another. It would be perceived instead as a mutual change of those their properties which are caused by interaction with the substance S. However, if just these properties of the objects are decisive (i.e. the objects themselves are identified by them), the result of the transformation W _M will be indeed perceived as a mutual conversion of “particles” and “antiparticles” and that of right and left objects.

Suppose that the transformation W _M causes no change in the World except interconversions of “particles” and “antiparticles” and those of right and left objects. These interconversions may be regarded as the results of two transformations: respectively, the charge conjugation C and the spatial inversion P. Therefore it may be written: W _M = CP, where P has the same center of inversion as W _M. The transformation , that is, sign reversion of the time direction , reverses the stream direction of the substance S with respect to M. It can be identified with the time reversion transformation T, considered in physics, the latter consisting in the sign change of the temporal variable t: = T. Substituting the above values of the transformations W _M and into Eqs. (8.5) and (8.6) and allowing for commutativity of the transformations, we obtain

(8.7)

(8.8)

Eqs. (8.7) and (8.8) correspond to the cases when the time substance S does not possess or possesses the W _S-symmetry, respectively. In (8.7) the inversions P and W _S should have the same center (as it has been proved previously, this condition is not compulsory if the substance S is homogeneous along each hyperplane parallel to M).

Thus, within the framework of the model being described, the phenomena observable in our World are characterized (under certain conditions) by the following symmetry. They are CPTW _S invariant if the time substance S does not possess the W _S-symmetry and are CPT invariant in the case of an W _S-symmetric substance S. This is the form in which the physical space-time symmetry appears when studied from inside our World. Meanwhile, the most complete description of the physical space-time symmetry under inversion transformations, independent of specific properties of the substance S, is given by the law (8.3). It is just the way an “external observer”, if he could look at the physical space-time “from outside”, would perceive the latter’s symmetry.

Relation to the CPT theorem. In Section 6 the arguments have been advanced in favor of the assertion that the “particles” and “antiparticles”, as they had been introduced here, might coincide with real particles and antiparticles. If this is indeed the case, all the transformations in Eq.(8.8) are identical to those used in physics with the same notations. Therefore the above conclusion concerning physical space-time symmetry may be regarded as an analogue of the well-known CPT theorem, a fundamental theorem of quantum field theory (Okun’ 1988). By this theorem, the equations of quantum field theory are invariant under the product of three transformations: charge conjugation C, spatial inversion P and time reversion T. The CPT theorem is conventionally treated as the most general manifestation of a symmetry law of nature. Note that the symmetry following from it corresponds, in the model we consider, to the particular case of an W _S-symmetric time substance S, i.e. to the case described by Eq.(8.8). At the same time the symmetry dictated by the more general formula (8.7) incorporates the transformation W _S ignored by the CPT theorem. It should be emphasized once more that the most general formula expressing the physical space-time symmetry under inversions, is Eq.(8.3).

Many divisions of physics, including non-relativistic quantum mechanics, a number of natural sciences: biology, chemistry, geology and others, are based on the conceptions of Newton’s classical mechanics regarding the properties of time and space. Let us transform the above substantial model of space-time to this case.

Classical mechanics postulates that space and time are absolute, i.e., independent of the states of physical systems and processes occurring in the World. Space is considered to be three-dimensional, proper Euclidean, and time to be one-dimensional, continuous and homogeneous (with respect to its geometric property of duration). In fact, time in classical mechanics is a universal scalar parameter equally varying (current) at all points of space. The space and time defined in this way can be unified to form a four-dimensional manifold possessing the geometry of real proper Euclidean space of signature (4, 0). This manifold will be called, as before, space-time. We will denote its metric form by g⁺.

Let us fix an orthogonal coordinate system corresponding to a certain inertial frame of reference in the “classical” space-time under consideration. Let {,,,} be the orthonormal tetrad of this coordinate system (here is the direction unit vector of the time axis, the remaining vectors are direction unit vectors of the spatial axes). By definition of an orthonormal tetrad and in view of the properties of the metric form g⁺ we have

(9.1)

In the tensor basis formed by pairwise tensor products of the vectors of this tetrad the metric form g⁺ looks as follows:

(9.2)

(cf. the expressions (9.1) and (9.2) with (2.9) and (2.15)).

The “classical” model of space and time under consideration is in complete agreement with the fundamental premise of relativity theory by which space and time form a unified four-dimensional manifold but violates another premise of this theory endowing this manifold with pseudo-Euclidean (in general, pseudo-Riemannian) geometry.

The results of calculations performed with the aid of the formula of special relativity are known to pass into the corresponding results obtainable within the frames of classical mechanics by making the dimensionless parameter v/c tend to zero (v is the velocity of motion of a physical system under study and c is the velocity of light in vacuum). At the same time, the metric form g of pseudo-Euclidean Minkowski space admits no limiting transition to the metric form g⁺ of proper Euclidean space-time, which is seen immediately when Eqs. (2.15) and (9.2) are compared. Therefore the model of space-time of classical mechanics should be constructed as an independent one, underivable from the corresponding constructions of relativity, although the two theories have much in common.

The initial postulate of the substantial model of space-time within the framework of classical mechanics can be formulated as follows.

Postulate I⁺. Time and space form a unified four-dimensional substance; the latter is endowed with geometry of real proper Euclidean space and possesses certain physical properties due to which it interacts with matter, physical fields and processes occurring.

The postulated object, as before, will be called the space-time substance or simply the time substance S. Further definitions and postulates repeat those introduced in Sections 3-8 actually word by word. Therefore, without presenting them again, let us consider Postulates II and III, along with the definitions of the World M, physical space-time, time direction , a “particle” and an “antiparticle”, right and left systems and the space-time inversion W to be valid in the “classical” model. Note that the situation here proves to be somewhat simpler than in the case considered before because in proper Euclidean space-time, unlike the pseudo-Euclidean one, the hyperplane of the World M and the time direction are unique for all the coordinate systems, while the time axes are parallel to one another.

The possibility of an extension of the definitions and postulates formulated above to the “classical” case is explained by the fact that they do not use the metric form signature explicitly, moreover, they are principally based on the affine properties of space-time, which are identical in the cases of proper Euclidean and pseudo-Euclidean geometries. Only the definition of a light cone may be called an exception. The concept of a light cone, based on the equality (2.6), cannot be introduced in the “classical” model in principle due to the absence of null vectors (nonzero vectors having a zero scalar square) in proper Euclidean space-time.

One more difference between the “classical” model and the “relativistic” one corresponds to its symmetry. Since Section 8 did not use the metric form signature in the analysis of model symmetry, its content may be entirely extended to the “classical” case. Hence the “classical” model has exactly the same symmetry under inversions as the “relativistic” one. Besides, everything that was said at the end of Section 8 concerning the relation of the symmetry law to the CPT theorem, is true for the “classical” model. At the same time, in the “classical” case, unlike the “relativistic” one, Eqs. (8.7) and (8.8) describing the symmetry of phenomena observable in our World, may be derived not only using discrete transformations of inversion, but with the aid of continuous ones, describing physical space-time rotation, as well. Note that in the “relativistic” case a similar derivation method cannot be realized due to the fact that the light cone is an insuperable obstacle for continuous rotation of the time axis in pseudo-Euclidean space-time. Indeed, if the time axis could pass from the interior of the light cone to its external domain in a rotation, then at the instant of crossing the light cone the unit vector would be converted into a null vector with a zero scalar square, which is impossible.

Let us formulate the symmetry law of the physical space-time under rotation transformations for the “classical” model.

Preliminarily we would like to remind that the rotation is realized: in two-dimensional space about a point, in three-dimensional space about a straight line and in four-dimensional one about a plane. We shall call the plane about which the rotation of a body in four-dimensional space is performed, the plane of rotation (in a similar way as the axis about which a body rotates in three-dimensional space is called the axis of rotation). Note that if material points forming the plane of rotation belong to the rotating object, then they rotate together with it, as well as do atoms lying on the rotation axes of the Earth or of a top. We notice this evident fact in order to emphasize that in the case of rotation of the whole physical space-time there remains no material point with respect to which this rotation might be fixed.

Let us introduce the following physical space-time transformations for the “classical” model:

Y , a rotation of the physical space-time as a whole by the angle 180° about some plane belonging to the World M;

Y _M, a restriction of the transformation Y onto the hyperplane of our World M, i.e. an overturn of the World M “upside-down”; it is performed by rotating the World M by 180° about one of the planes belonging to it; it leaves the time substance S and the time direction unchanged;

Y _S, a restriction of the transformation Y to the time substance S, i.e. a rotation of the substance S as a whole by 180° about some plane belonging to the World M; it is performed without changing the World M and the time direction ;

, sign reversal of the time direction , i.e., reversal of the World motion along the time axis (identical to the transformation from Section 8).

We shall assume that the rotations Y , Y _M and Y _S not only turn objects but, like the transformations W , W _M and W _S, change their vector characteristics in a certain way. Namely, for each vector characteristic they reverse the signs of the two (out of four) components which are orthogonal to the plane of rotation (they as though turn these components along with the object by 180° ). Evidently the rotations Y , Y _M and Y _S can be realized in a continuous way, i.e. by a continuous set of isometric transformations of the corresponding object.

The physical space-time, as it is seen directly from Fig.2, will transform into itself after performing the following transformations: an overturn of the World M “upside-down” by a rotation about a certain plane lying in it (the transformation Y _M); a reversal of the World motion along the time axis, i.e. the sign reversal of the time direction (); a rotation of the time substance S by 180° about the same plane lying in M (Y _S); finally, a rotation of the whole construction by 180° again about the same plane (Y ). Hence it follows that in the “classical” case the law of physical space-time symmetry under rotation transformations is expressed by the formula

(9.3)

where I is, as before, the identity transformation. It should be stressed here that all the transformations should be performed at the same instant and, in addition, the rotation planes should coincide for the transformations Y , Y _M and Y _S. The requirement of coinciding rotation planes may be removed if the time substance S is homogeneous along each hyperplane parallel to the World M. This is proved by a method similar to that used in Section 8 to prove a similar statement with respect to formula (8.3).

The remaining content of the present section is devoted to derivation of Eqs. (8.3), (8.7) and (8.8) on the basis of the symmetry law (9.3).

Denote by F , F _M, F _S the rotations of the whole physical space-time, the World M as a whole and the time substance S as a whole, respectively, by 180° about a plane containing two crossing straight lines, one of which lies in M and the other is orthogonal to M (i.e., parallel to the time axis). By analogy with the case of the above rotations we shall assume that the rotations F , F _M, F _S reverse the signs of two out of the four components of each vector characteristic of an object being turned, namely, those which are orthogonal to the plane of rotation. The rotations F , F _M, F _S may be realized continuously, in such a way that each hyperplane of simultaneous events belonging to the object being turned, will be translated only along itself. Note that the rotations Y , Y _M and Y _S do not possess such a property: any continuous realization of these rotations extracts the hyperplanes of simultaneous events out of their “bedding hyperplanes”. This difference between the two types of rotations may be clarified on the example of rotation of a two-dimensional plane in three-dimensional proper Euclidean space. Being rotated about an axis perpendicular to it, a plane translates along itself (Fig.9a). Unlike that, in the case of rotation about an axis lying in it, a plane goes out of its “bedding plane” (Fig.9b).

We present two lemmas, of which the first one describes some properties of the rotations considered and the second one establishes an interrelation between the transformations Y , F and W .

(9.4)

, (9.5)

where the operators entering into a single equality have a common plane of rotation in M and are realized at the same instant.

Proof. It is evident that the physical space-time after two successive rotations by 180° about the same plane passes to its initial state. This means that Y Y = I, whence Y - ¹ = Y . Similar equalities also are valid for the other rotations and sign reversal transformation involved in (9.4) and (9.5). Therefore the first four equalities from (9.4) and the first three in (9.5) are true. The last one from (9.4) evidently follows from the symmetry law (9.3) and the relation Y - ¹ = Y . The rotation F is carried out about a plane parallel to the time axis, hence it conserves the vector characterizing the mutual motion of the World M and the time substance S. Consequently, the transformation F consists only in rotation of the World M and the substance S, which is reflected by the last equality from (9.5). Thus, the lemma has been proved.

I b ), (9.6)

where the symbols in parentheses by the rotation and inversion operators denote the plane of rotation and the center of inversion, respectively; a is an arbitrary plane lying in the World M; b is the plane containing two crossing lines: the normal to a lying in M and the straight line orthogonal to M (a I b is a onepoint set). Similar equalities are also valid for the transformation triads Y _M, F _M, W _M and Y _S, F _S, W _S.

Proof. Let us introduce an orthogonal coordinate system in the physical space-time, with the origin at the point a I b , two axes lying in the plane a and other two axes posed in the plane b (evidently such a coordinate system exists). Let us perform a rotation Y of physical space-time about the plane a . It leads to a 180° rotation of the coordinate axes situated in the plane b . Now let the physical space-time be subject to rotation F about the plane b . In this case the axes lying in the plane a turn by 180° . As a result, the directions of all the four coordinate axes turn out to be reversed. Since the rotations leave mutual arrangements of the points of physical space-time unchanged, all its points in the new state have the same coordinates in the turned coordinate system as they had in that system in the initial state. Hence, with respect to the coordinate system in its position before the rotation, all points of the physical space-time change the signs of their coordinates, which means a reversal of their radius vectors. The vector characteristics of the physical space-time also reverse their directions in this procedure, since the rotation Y changes the signs of their two components perpendicular to the plane a , while the rotation F changes the signs of their two components perpendicular to the plane b . Hence it follows that the superposition of rotations Y F is equivalent to the space-time inversion W centered at the origin a I b . This conclusion is evidently independent of the succession of performing the rotations. Therefore Y F = F Y = W , i.e. the equality (9.6) is true. The above considerations remain valid if the physical space-time is replaced by the World M or the time substance S, hence similar equalities are fulfilled for the transformation triads Y _M, F _M, W _M and Y _S, F _S, W _S, which completes the proof.

Let us continue the analysis of the model symmetry.

As a result of two successive rotations by 180° about the same plane, the physical space-time passes into itself, therefore F F =I. From Lemma 4 it follows that F =F _{SF M}. A combination of these equalities gives F F _{SF M} = I. Hence the left-hand side of formula (9.3) does not change its value being multiplied by F F _{SF M}. Performing such a multiplication and using the commutativity of the transformations, we find:

(Y F )(Y _{SF S})(Y _{MF M}) = I .

Based on Lemma 5 and the equality = , from this relation we obtain the symmetry law for the “classical” model under inversions:

, (9.7)

here the centers of all inversions are at the intersection point of the rotation planes of the transformations Y and F . Eq.(9.7) coincides with Eq.(8.3) from Section 8. This result once again proves the identity of symmetries of the “classical” and “relativistic” models under inversions.

Now let us derive Eqs.(8.7) and (8.8). Evidently it can be done with the aid of the law (9.7) in the same way as in Section 8. We shall, however, act otherwise and obtain these formula from the symmetry law (9.3).

It is natural to admit that the transformation Y does not lead to observable changes in the World, since according to Postulate III there exists no reference body independent of M and S with respect to which a turn of the whole construction depicted in Fig.2 might be considered. Therefore when the symmetry of the physical space-time is studied from inside the World, the law (9.3) will have the form

. (9.8)

Let F _M be a rotation about the plane that passes through two straight lines: the normal to the rotation plane of the transformation Y _M, which lies in M, and the straight line orthogonal to M and crossing that normal. Then by Lemma 5

, (9.9)

where the center of the inversion W _M coincides with the intersection point of the rotation planes of the transformations Y _M and F _M. Hence one can see that an inversion of the World M can be realized by two successive rotations, one of which is associated with the World going out of its “bedding hyperplane”, while the other is performed by World motion along itself.

It has been mentioned previously that the inversion W _M leads to interconversions of “particles” and “antiparticles”, as well as that of right and left objects. Let us assume, as it was done in Section 8, that there occur no other changes in the World under the inversion W _M. Then W _M = CP, where (recall) C is charge conjugation; P is a spatial inversion; here P has the same center of inversion as W _M. In Section 8 it has been indicated that = T, where T is time reversion. Using the values of transformations W _M, written above, along with (9.9) and the fact that =, we come to the equalities

(9.10)

A substitution of these expressions into (9.8), with allowance for transformations commutativity, gives

(9.11)

According to Lemma 4, F = , hence F = F . Neglecting here the transformation F as unobservable from inside the World, we have = . From this condition and Lemma 5 we find: ==, where, as easily seen, the center of inversion coincides with the center of the transformation P. A substitution of this value of the product to (9.11) yields the formula to be found

(9.12)

In the particular case of an W _S-symmetric time substance S Eq.(9.12) takes the form

(9.13)

Eqs. (9.12) and (9.13) describe the physical space-time symmetry as studied from inside the World; they coincide exactly with Eqs. (8.7) and (8.8) from Section 8 obtained by inversion transformations.

Thus, in the case of the “classical” model the use of both continuous rotation transformations and discrete inversion transformations leads to the same conclusions concerning the symmetry of observable phenomena of our World, with this symmetry proving to be the same as in the “relativistic” case.

On the whole one can say about the “classical” substantial model of space-time that the results of Sections 3-8 are practically completely applicable to it; this is due to the fact that they are based mainly on affine (rather than metric) properties of space-time.

The models of space and time considered in classical mechanics, special and general relativity, relativistic theory of gravity and other physical theories, have a common feature: in all the models there is a concordance of time stream tempo in different frames of reference. Thus, in classical mechanics, employing the conception of absolute time, the latter even streams at exactly the same tempo in all frames of reference. In special and general relativity and in some other theories the time stream tempo can be different in different frames of reference, however, it is connected by a quite definite dependence for different frames. (Furthermore we will mention, for brevity, only special and general relativity, although the conclusions to be made are applicable to other theories as well.)

As known from relativity theory, the time stream tempo is determined by the geometry of the space-time manifold, or, more precisely, by the local value of the metric form. Therefore, from the viewpoint of mathematics, the concordance of time stream tempo is a consequence of the existence of such a metric form field on the space-time manifold that the metric form values are mutually coordinated at different points of the manifold, i.e., connected by a certain functional dependence. In special relativity the metric form field is assumed to be homogeneous, therefore the above functional dependence is just an identity. In general relativity, where the metric form field may be inhomogeneous, this dependence is expressed in the form of the Einstein equations.

The common feature of the models discussed here, the concordance of the time stream tempo, or, more generally, the concordance of the values of the metric form in different points of space-time, is confirmed by experiment and hence correctly reflects the properties of nature. Therefore it is natural to ask the following question: “What is the cause of the time stream tempo concordance (metric form value concordance) in different points of space-time?”

It would be unrealistic to believe that the concordance we are dealing with is just a coincidence occurring by accident. Indeed, if one even admits that at the birth of the Universe the metric form and thereby the course of time were perfectly coordinated at all points, but there existed nothing able to maintain that coordination, then the many billions of years of Universe evolution would certainly lead to a disagreement of those values even at points of the Universe close to each other. Thus time and the metric form would have become random functions of the spatial coordinates. However, it has not happened. Therefore it remains to admit that there exists a certain objective cause, more weighty than a mere accident, able to provide the concordance.

It is easily assured that neither of the known physical fields or material bodies can constitute such a cause. Indeed, as follows from general relativity, when the energy of all fields and masses of all bodies tend to zero, the space-time manifold evolves from a pseudo-Riemannian one, having a nonzero curvature tensor, to a pseudo-Euclidean manifold (Minkowski space) where the curvature tensor is identically zero. As was done, the metric form becomes the same everywhere and time begins to flow at the same tempo in all frames of reference which are mutually at rest. Thus, after a transition to empty space-time the concordance of interest is not only unviolated but even actually turns to an entire identity. Therefore, indeed, no field or material body can be a cause of the time stream tempo and metric form value concordance at different points of space-time.

Surprisingly, in physical publications the problem of a cause of metric concordance is not investigated. And herewith such a second-order effect as the possibility of metric distortion by matter and physical fields is discussed in much detail, although its influence on the scale of the part of the Galaxy surrounding us is negligibly small. Moreover, based on this effect, the conceptual proposition is adopted that just matter and the physical fields create the space-time metric, the proposition regarded to be a decisive argument in favour of the relational conception of time. Meanwhile, this proposition is in sharp contradiction with the fact that the main term in the expression for the metric form, the one corresponding to empty space-time, in no way depends on the properties of matter and physical fields.

Thus one may assert that, first, the metric concordance at different points of space-time is maintained by some objective cause, in other words, there is a material object providing the concordance, and, second, manifestly neither matter, nor physical fields can constitute that object. Hence it follows that within the modern physical theories which consider matter and fields to be the only material objects, it is impossible in principle to obtain an answer to the above question.

Meanwhile, the substantial model of space-time leads to an easy solution of this problem. Since, according to Postulate I, the time substance S is the carrier of the space-time metric, one can quite definitely assert that just that substance provides metric concordance at different space-time points: this concordance is a direct consequence of the unity of the substance properties in its whole volume.

However, it should be noted that this assertion is still not a complete answer to the question of interest. The point is that the idea of metric concordance, being the basis of the above considerations, has been taken from modern theories of space and time. Meanwhile, in those theories the metric concordance is not a characteristic of the space-time substance (it does not appear in those theories at all) but that of matter and fields. Therefore the assertion that it is the substance S that provides metric concordance, should be supplemented by an explanation of how it endows the matter and fields with its metric. The explanation turns out to be very simple if the World and the time substance are interrelated in quite a definite way. The next section is dedicated to working out this interrelation in detail.

The substantial model of space-time under consideration admits different versions of relations between our World (i.e., matter and physical fields) and the time substance S.

By one of the versions, our World and the substance S are mutually independent physical realities. At first sight such an approach appears to be plausible; however, it is unsatisfactory because it leaves unresolved the problem of metric transfer from the substance S to the matter and fields. The situation is further aggravated by the fact that if the matter and the fields are independent of the substance S, it is admissible to consider a limiting case when there is no substance S at all. What happens in such a case? Are the matter and the fields left without a metric, or, maybe, they possess a specific metric of their own, which, according to the contents of Section 10, can be uncoordinated in different space-time points? No apparent answer to these questions is seen. Meanwhile, as shown by practice, if the foundations of a theory leave unanswered any questions of this kind, concerning the most fundamental features of the phenomena to be described, there is little hope that such theory would answer them after a deep elaboration.

However, another version of the relations between the World and the time substance is possible. We will take this version as a basis. It is established by the following postulate.

Postulate IV. The matter and all the physical fields which form our World are not independent physical entities but are specific structures of the space-time substance. Our World as a whole is a solitary wave (like a soliton) propagating in the space-time substance.

The adoption of this postulate is justified by a primary nature of the notions of space and time as compared with those of matter and field; this nature manifests itself in the fact that the former can, at least in principle, exist without the latter, while the reverse is not true. Indeed, the idea of Minkowski space, unfilled with matter or fields, is quite meaningful as long as it can be given a rigorous mathematical description; unlike that, the idea of a material body having no spatial characteristics, in particular, occupying no (even zero) spatial volume, as well as the idea of a material process having no temporal characteristics, are deprived of any physical content.

If the time substance S is endowed with pseudo-Euclidean geometry, the wave of our World, mentioned in Postulate IV, is, in general, different in different coordinate systems (although its propagation directions are coordinated, see Section 2). If, on the contrary, it is endowed with proper Euclidean geometry, then the wave of our World is unique for all the coordinate frames. Note that in both these cases the wave of our World has a flat shape. If the model is extended to the case studied by general relativity, the substance S should possess the geometry of a pseudo-Riemannian space. Thereby, due to specific effects predicted by this theory, both the substance S and our World wave will be appreciably curved near structures of high energy.

Thus by Postulate IV the matter and fields are certain structures of the time substance (like condensations, vortices, dislocations, etc.). In such a version of the relations between the World and the time substance the problem of metric transfer from the substance to the matter and fields, posed in Section 10, is resolved at once. As matter and fields are specific states of the substance itself, no special metric transfer is required since these objects have a common metric with the substance from the outset.

It is easily verified that Postulate IV leaves unchanged all the constructions of the previous sections.

Apparently just one of the propositions of the previous sections could cause doubt as regards the possibility of its extension to the case considered. It concerns the use of inversions and rotations which transform the World M and the time substance S separately from each other. (Such transformations were used when the model symmetry was analysed.) The plausibility of using these transformations can be easily illustrated again on the example of dislocations in a crystal. The fact that a dislocation is a structure over a crystal lattice, as it is well known, does not exclude the possibility of different positions of a dislocation with respect to the lattice. Similarly, in the case of the World M the fact that it is a structure of the time substance is not by itself an obstacle for realizing its different positions with respect to the substance S. Therefore in the present version of the model it is admissible to use the inversions W _M and W _S and the rotations Y _M, Y _S, F _M and F _S which transform the World M and the substance S independently of each other. Therefore all the conclusions of Sections 8 and 9 concerning the model symmetry, remain valid for the model version incorporating Postulate IV as well.

We would like to restrict the discussion of the present version of the model to a few brief comments.

Evidently, the idea of a time substance satisfying Postulate IV, is in some respects close to the quantum-field-theoretical concept of physical vacuum from which particles of matter are created. Meanwhile, our model is free of a certain ambiguity inherent in the physical vacuum concept. The latter consists in the fact that the term “vacuum” in its very sense denotes emptiness, i.e., absence of anything at all, and at the same time in quantum field theory vacuum is endowed with certain physical properties, i.e., is actually treated as a material object. Such an ambiguity certainly cannot favour further development of the theory.

The suggested model version observes the famous Occam principle (Okun’ 1988, p.187) claiming that essences should not be multiplied without necessity. Here, instead of numerous sorts of matter and physical fields there is only one essence, the time substance, while all the rest is just its structures.

The fact that modern physical theories are successful in describing the properties of matter and fields without addressing to a time substance forming them, does not mean that such a substance is absent. Recall that lately in the 19th century it was also believed (Physicists Joke 1966, p.32) that the then available physical theories were quite sufficient for describing the properties of matter, although nothing was known about the elementary particles forming it. By the way, modern physics is successful in doing without the notions of life, man, consciousness (such notions are just absent in either “Physical Encyclopaedic Dictionary”, or in subject indices to the ten volumes of “Theoretical Physics” by L.D.Landau and Ye.M.Lifshitz), which nevertheless does not mean that those phenomena do not exist.

A difference between the presently introduced time substance and the known ether models is as follows. The time substance S is four-dimensional, while ether is three-dimensional. The substance S flows across our World normally to it, while ether is at rest with respect to the World as a whole (in this connection it is often considered as an absolute frame of reference). The substance S possesses pseudo-Euclidean geometry and therefore satisfies all the statements of special relativity while ether is commonly endowed with proper Euclidean geometry, leading it to contradictions with relativity.

That the time substance has not yet been discovered by experiment, can be explained by the fact that the physical instruments available and our organs of sense are able to interact only with matter and fields but not directly with the time substance forming them.

Thus the suggested substantial model of space-time in its version incorporating Postulate IV, easily resolves the question of why the metric is coordinated in different space-time points, the question having no answer in modern physical theories. This version of the model reduces the properties of all the physical objects of our World to those of the time substance. A further development of the model should consist in concretizing physical properties of the substance which would satisfy Postulates I - IV.

Space-time as a four-dimensional substance and the three-dimensional World moving through it are the basic features of the suggested model. It gives a clear meaning to the notions of time flow and time direction and easily proves a proposition on the World symmetry similar to the CPT theorem of quantum field theory, while the method of specifying space-time coordinates is brought into correspondence with that adopted in mechanics. It is shown that the observed mirror asymmetry of the World, along with its asymmetry with respect to particles and antiparticles, can be consequences of the action on the World exerted by the space-time substance. A version of the model has been suggested in which our World is a specific structure of the space-time substance. It has been possible to obtain all these results without knowing the physical properties of the substance. Their specification is a subject of further investigations.

N.A.Kozyrev’s results concerning the properties of time and those of the present paper constitute just an initial stage in the development of the substantial model of space-time; however, even they testify that this model has a rich potential. Therefore the question taken as the title of the present article, namely, “What can be obtained from the substantial conception of time?”, is to be answered in the following way: this conception can give an understanding of the essence of space and time, the basic concepts of natural science, which would be deeper and more adequate to reality than the existing one.

The author expresses his deep gratitude to E.L.Aero, A.D.Alexandrov, V.A.Antonov, A.D.Chernin, Yu.M.Dal', Yu.I.Kopilevich, S.E.Kozlov, A.V.Krivov, A.P.Levich, V.M.Lomovitskaya, K.L.Malyshev, V.V.Orlov, Yu.A.Romashov, V.A.Shvetsova, A.V.Soldatov, A.A.Vakulenko and S.I.Vasilyev for discussing the papers included in the present edition and for useful comments which provided a refinement of some propositions of the theory.

REFERENCES