Реляционная статистическая модель часов
и ОПИСАНИЕ ФИЗИЧЕСКИХ свойств времени
§1. Введение
Описывается теоретическая модель часов и связанная с ней модель времени, которая основывается на учете осредненного движения всех частиц мира. Попытка установления связи между временем и движением — один из традиционных подходов к пониманию природы времени. Не останавливаясь на историческом обзоре реляционных представлений о пространстве-времени (они имеют давнюю традицию и восходят к античности), можно сказать, что в новейших физических теориях, и прежде всего в теории относительности, реляционные представления получили подтверждение.
Но несмотря на то, что в теории относительности пространство-время обрело новый единый четырехмерный статус (это связано с фундаментальным характером скорости света), приборы, применяемые для измерения времени и расстояния (часы и линейки), имеют принципиально различный характер. Анализ пространственных и временныў х величин позволяет поставить вопрос: нельзя ли свести две различные процедуры измерения к одной (выступающей, естественно, в различных функциях для времени и пространства)? “Время” в таком понимании, в такой модели будет представлено в виде некоторой функции от величин, которые получены путем измерения с помощью масштабной линейки. Данное математическое уравнение будет положено в основу предлагаемой теории, и, исходя из него, будут выводиться кинематические и динамические соотношения (аналоги законов сохранения и уравнений движения).
Такой подход, по-видимому, близок к принципу Маха, понимаемому здесь как некий обобщенный философский принцип, определяющий связь пространства-времени с движением физических тел (о формулировке инерционных свойств в принципе Маха в модели говорится в §3). Во всяком случае, в предлагаемых построениях реализуется представление о том, что время течет, поскольку есть движущиеся частицы.
На важность моделирования масштабов и часов указывали различные физики и философы. Приведем только несколько цитат известных авторов.
А.Эйнштейн (1967): “...собственно говоря, теорию масштабов и часов следовало бы выводить из решений основных уравнений (учитывая, что эти предметы имеют атомную структуру и движутся), а не считать ее независимой от них. Обычный образ действия имеет, однако, свое оправдание, поскольку с самого начала ясна недостаточность принятых постулатов для обоснования теории масштабов и часов. Если вообще не отказываться от физического толкования координат (что само по себе было бы возможно), то лучше уж допустить такую непоследовательность, но с обязательством избавиться от нее на дальнейшей стадии развития теории”.
А.Пуанкаре (1983): “Таким образом, пространство в действительности аморфно, оно — рыхлая лишенная твердости форма, которую можно приложить ко всему; оно не имеет своих собственных свойств. Заниматься геометрией — это значит изучать свойства наших инструментов, т.е. свойства твердого тела. ... То, что мы сказали о пространстве, применимо и ко времени. Говоря это, я имею в виду не время, как его понимают ученики Бергсона, не ту длительность, которая не является чистым количеством, лишенным всякого качества, но которая является, так сказать, самим качеством, длительность, различные части которой, взаимно проникая друг в друга, качественно друг от друга отличаются. Эта длительность не могла бы быть инструментом ученого; она могла бы стать им, лишь подвергнувшись коренному преобразованию, лишь “опространствившись”, как говорит Бергсон. Действительно, необходимо, чтобы она стала измеримой; то, что недоступно измерению, не может быть и объектом науки. Но измеримое время по существу также относительно. Если бы все процессы в природе замедлились и если бы то же самое произошло с нашими часами, то мы бы ничего не заметили... Таким образом, свойства времени — только свойства часов, подобно тому как свойства пространства — только свойства измерительных инструментов”.
В.Паули (1975): “Думаю, что после того, как существование материи найдет свое выражение в математическом языке теории, построить модель часов будет не очень трудно. Все сходятся на том, что часами следует называть не любую систему, а лишь такую, которая измеряет собственное время ds2”.
В последнее время обсуждались возможные теоретические концепции о пространстве и времени в физике. С точки зрения предлагаемой модели интерес представляет проблема “макроскопического пространства и времени”. Из современных авторов, затрагивающих этот вопрос, можно назвать Дж.Чу и Е.Циммермана. Е.Циммерман (1962) высказывает предположение о том, что пространство-время возникает из взаимодействия частиц, подобно термодинамическим величинам, применяемым только к макроскопическим объектам (правда, никакой математической модели не предлагается).
В наших построениях ход часов будет моделироваться с помощью функции от определенным образом учитывающегося движения очень большого числа частиц (в пределе его можно полагать равным, например, количеству нуклонов в Метагалактике — это так называемое число Эддингтона, с точностью до нескольких порядков, равное 1080).
Такие представления о свойстве часов (и соответственно времени в физике) связаны с тем, что в любых обычных часах всегда реализуется движение некоторого физического объекта (Солнца, стрелки часов и т.д.). Однако ход часов нельзя сопоставить с движением произвольно выбранного тела, так как это физическое тело в заданной системе отсчета может, к примеру, остановиться. Наше сложившееся представление о приемлемых часах связано с пониманием хода часов как непрерывного и равномерного процесса. Под непрерывностью понимается свойство постоянства течения времени, передаваемое часами, предполагается, что идеальные часы должны идти постоянно (конечно, конкретные часы могут остановиться, но “сумма” всех часов, в том числе всех природных движущихся объектов, должна передавать течение времени). Равномерность пока понимается в интуитивном смысле (о проблеме равномерности времени речь будет идти в §6). Оба указанных свойства могут быть удовлетворены, если мы рассмотрим осредненное движение N частиц, составляющих рассматриваемую систему, которая будет моделировать сумму движения частиц в мире. Причем движение каждой частицы будет определяться как пространственное перемещение между двумя опытами без изначального понятия времени.
В отличие от традиционных часов, конструируемых на основе использования периодических процессов, предлагаемая модель оперирует со случайными движениями частиц. Осреднение по большому числу частиц приводит к тому, что отличия от стандартного подхода невелики и определяются статистической ошибкой, зависящей от числа частиц. При стремлении числа частиц к бесконечности может реализовываться соответствие данного подхода и традиционной модели. Обычно подчеркиваемая важность именно периодичности, представленной в часах, на наш взгляд, является вторичным признаком, позволяющим удобно ввести единицу времени (легко представить часы, представляющие собой такое устройство: стрелка, расположенная над бесконечной равномерно протягиваемой лентой с нанесенными на ней делениями единиц времени с увеличивающимися числами). В часах важнее свойство равномерности, причем равномерное движение имеет “исторический” характер, поскольку ход идеальных часов все время корректируется путем подстройки под движение астрономических и других объектов.
Временноў й интервал между двумя опытами, в которых фиксируются пространственные положения всех частиц, определяется как среднее от квадратов приращений радиусов-векторов частиц. Характерным в модели конструируемых “мировых” часов является то, что здесь используется интегральная характеристика, охватывающая максимально допустимое число частиц в системе (т.е. все наблюдаемые частицы в мире), с другой стороны, важно то, что интервал времени вводится для инфинитезимального перемещения всех частиц. Это означает, что в основной формуле будут связаны некоторые интегральные и дифференциальные характеристики системы (но не в рамках вариационного принципа).
Исходя из основного уравнения, задающего интервал времени через указанные перемещения частиц, выводятся преобразования Галилея и аналоги уравнений движения, строится релятивистское обобщение, изучаются возможные отличия от традиционной теории, связанные со статистичностью модельного времени.
В предлагаемой модели дается количественное выражение утверждению, что время является мерой изменения состояния системы, понимаемой как сумма пространственных характеристик всех частиц этой системы. Вводимое понятие состояния системы характеризует момент модельного времени. (Движение, воспроизводимое в часах, определяется через разность близких в некотором смысле состояний.) Это позволяет делать различные заключения о свойствах данного времени, в частности, поставить вопрос о понятии необратимости в модели. В заключительном параграфе обсуждаются возможности и перспективы таких представлений. Помимо “мирового” времени можно рассматривать время для подсистемы с меньшим числом частиц, такие вложенные друг в друга времена могут образовывать определенную иерархию. Обсуждаются также возможности обобщения модели.
§2. Основные положения модели и получение
кинематических соотношений классической механики
Для построения классических часов рассмотрим систему N частиц. Частицы будем считать одинаковыми, это будет проявляться в том, что в основную сумму будут входить только их кинематические характеристики (перемещения). Время будет определяться через движение всех рассматриваемых частиц. Движение задается как изменение пространственного положения частиц в заданной системе отсчета.
Как известно, системой отсчета обычно называют геометрическую систему отсчета, дополненную часами (континуальное множество геометрических точек, расстояния между которыми фиксированы, называют геометрической твердой средой, которая и принимается за геометрическую систему отсчета). Для задания системы отсчета рассмотрим систему неподвижных относительно друг друга частиц (понятие “неподвижные” будет расшифровано далее). Пусть это будут частицы с номерами 1, ..., L (предполагается, что всем частицам в мире можно сопоставить определенные номера). Такая дискретная система будет являться приближением для абстрактной континуальной твердой среды. В предлагаемой модели время не является изначально задаваемой величиной, поэтому часы не будут фигурировать в качестве элемента системы отсчета. Время будет задаваться с помощью движения всех частиц системы.
Определим, что будет пониматься под пространственным перемещением (движением) частиц. Будем предполагать, что имеется физический сигнал, с помощью которого могут быть связаны все пространственные точки. Для определенности будем считать, что в качестве такого сигнала выступает свет. В каждой точке пространства (для заданной системы отсчета вводится система координат) поместим некоторый идеализированный прибор — “фотоаппарат”. С помощью этого прибора можно фиксировать положения всех частиц мира, т.е. получать “фотографии”. Если взаимное положение некоторого набора частиц (например, с номерами 1, ..., L) на различных “фотографиях” не меняется, то такую совокупность частиц можно считать “неподвижной”. С помощью такого “неподвижного” тела фактически и вводилась система отсчета.
Зададим в выбранной системе отсчета декартову систему координат. Тогда на “фотографиях” можно фиксировать положение всех частиц мира у соответствующих отметок координатной системы. Это означает, что каждой частице на данной “фотографии” можно поставить в соответствие определенную координатную отметку. Назовем “опытом” набор радиусов-векторов всех частиц, полученных с помощью указанного прибора, находящегося в некоторой точке (например, в А), т.е.
R(A) = {![]() , ...,
, ..., ![]() }.
}.
Здесь, как указывалось, значение ![]() определяется по видимой на “фотографии” отметке координат, находящейся рядом с i-й частицей.
определяется по видимой на “фотографии” отметке координат, находящейся рядом с i-й частицей.
Рассмотрим вначале классическую нерелятивистскую модель, соответствующую случаю, когда скорость света будет бесконечной и абсолютное время можно ввести естественным образом (о релятивистском обобщении речь будет идти в §5). Будем считать, что в точках системы отсчета, которые связаны одним и тем же сигналом (лучом света) с точкой А, будут идентичные по взаимному расположению частиц “фотографии” и одинаковые “опыты”. Их естественно отнести к одному моменту вводимого времени. Поэтому в заданной системе отсчета достаточно одного прибора (“фотоаппарата”), например, в начале координат. (для традиционной нерелятивистской системы отсчета, как известно, достаточно только одних часов в начале отсчета, так как здесь нет проблемы определения одновременности пространственно-разделенных событий.)
Будем вводить время t модели (связь этого теоретического времени с временем tc, измеряемым по обычным физическим часам, устанавливается дальше). Потребуем, чтобы величина приращения времени dt была функцией от изменения пространственного положения всех частиц. Заранее можно указать желаемые свойства для этой функции:
1) обращается в нуль, когда все ее аргументы равны нулю;
2) неотрицательна при любых значениях аргументов, что соответствует однонаправленности времени, моделируемому в обычных часах (вопрос об обратимости времени затрагивается в §6);
3) симметрична относительно всех своих аргументов (это связано с тем, что пока все частицы в модели считаются одинаковыми).
Пусть получены два опыта
![]()
Будем предполагать, что между этими “опытами” частицы переместились на дифференциально-малые расстояния, т.е.
![]() .
.
Промежуток времени dt, протекшего между двумя этими “опытами”, определим так:
 . (2.1)
. (2.1)
Причем, поскольку все перемещения дифференциально-малые (для этого надо нажимать на затвор “фотоаппарата” достаточно быстро), исключается возможность перемещения частиц “туда и обратно”, что могло бы привести к тому, что ![]() равнялось бы нулю (если бы все частицы ко второму “опыту” вернулись в прежние положения).
равнялось бы нулю (если бы все частицы ко второму “опыту” вернулись в прежние положения).
Отметим, что величина ![]() равна нулю не только в случае равенства нулю всех приращений
равна нулю не только в случае равенства нулю всех приращений ![]() , но и когда все
, но и когда все ![]() равны среднему значению
равны среднему значению ![]() , т.е. когда все частицы движутся одинаковым образом. В принципе равенство нулю приращения времени в этом случае можно было бы считать естественным ограничением модели — это означало бы, что время не течет, если весь мир движется как некое неразделимое целое. Однако в рамках принятых предположений такой случай не реализуется, так как есть L неподвижных относительно друг друга частиц (“неподвижное тело”, с помощью которого задается система отсчета), легко видеть, что, если только все частицы не покоятся относительно данных L частиц, то dt не равно нулю.
, т.е. когда все частицы движутся одинаковым образом. В принципе равенство нулю приращения времени в этом случае можно было бы считать естественным ограничением модели — это означало бы, что время не течет, если весь мир движется как некое неразделимое целое. Однако в рамках принятых предположений такой случай не реализуется, так как есть L неподвижных относительно друг друга частиц (“неподвижное тело”, с помощью которого задается система отсчета), легко видеть, что, если только все частицы не покоятся относительно данных L частиц, то dt не равно нулю.
Значок (A), отмечающий точку, в которой расположен “фотоаппарат”, в соответствии с предыдущими рассуждениями можно опускать. Будем полагать множитель a постоянным. Для нерелятивистского случая величина a не имеет фундаментального значения и является некоторым переводным коэффициентом с размерностью частного от деления единицы вводимого времени на единицу расстояния. В релятивистском случае a будет связана со скоростью света c (см. §5).
Скорость каждой частицы определяется естественным образом
![]() . (2.2)
. (2.2)
Из (2.1) и (2.2) следует соотношение
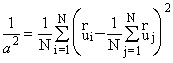 , (2.3)
, (2.3)
т.е. величина 1/a равняется среднеквадратичной скорости всех частиц.
Введение модельного времени по формуле (2.1) оправдано тем, что вычитание величины ![]() , характеризующей движение “центра масс”, приводит к тому, что dt2 описывает сумму только “хаотической части” N частиц. Данная статистическая сумма аналогична той, которая возникает для выражения температуры (в кинетической теории газов), где последняя определяется как среднее от суммы квадратов отклонений скоростей частиц от их средней скорости. Однако в основной формуле (2.1) есть и существенное отличие — здесь связываются инфинитезимальные величины, причем в правой части они объединены в сумме, т.е. здесь присутствует и некоторая интегральная величина (естественно, можно попытаться ввести обобщение, переходя от суммы к некоторому интегралу по всей массе системы).
, характеризующей движение “центра масс”, приводит к тому, что dt2 описывает сумму только “хаотической части” N частиц. Данная статистическая сумма аналогична той, которая возникает для выражения температуры (в кинетической теории газов), где последняя определяется как среднее от суммы квадратов отклонений скоростей частиц от их средней скорости. Однако в основной формуле (2.1) есть и существенное отличие — здесь связываются инфинитезимальные величины, причем в правой части они объединены в сумме, т.е. здесь присутствует и некоторая интегральная величина (естественно, можно попытаться ввести обобщение, переходя от суммы к некоторому интегралу по всей массе системы).
Будем изучать преобразование кинематических характеристик при переходе между системами отсчета, находящимися в относительном движении. Будем считать, что если в двух находящихся рядом точках разных систем отсчета (пусть это будут точки A и Aў ) получены “фотографии”, то образы всех частиц на “фотографиях” совпадут. это согласуется, по-видимому, с предположением об одинаковой для всех систем отсчета бесконечно-большой скорости сигнала и возможностью связать все частицы единым сигналом. Но хотя образы частиц при наложении “фотографий” полностью совпадут, координатные отметки рядом с этими образами будут различными, поскольку координаты точек A и Aў (каждые в своей системе отсчета и системе координат) в общем случае будут различными. В силу однородности и изотропности пространства эти отличия для всех координатных отметок будут равны различию в координатах точек A и Aў .
Рассмотрим две системы отсчета, движущиеся относительно друг друга. Пусть первые “опыты” для каждой из этих систем получены, когда начала отсчета их были совмещены. Имеем
![]()
где O и Oґ — начала отсчета “лабораторной” и “штрихованной” систем отсчета соответственно.
Второй “опыт” получим, когда точка Oґ сместится относительно точки O и будет находиться рядом с некоторой точкой A “лабораторной” системы отсчета. Получаем
![]()
причем в силу сказанного выше “опыты”, полученные для этого момента времени в точках A и O, полностью совпадут, т.е.
![]()
Все координатные отметки, полученные во втором “опыте” для “штрихованной” системы отсчета, будут отличаться от координатных отметок “лабораторной” системы на величину сдвига точки A относительно точки O. Этот сдвиг равен
![]() .
.
Здесь под ![]() подразумевается радиус-вектор точки O, который определяется в 1-м “опыте” (так как точка O — начало координат, то в данном случае
подразумевается радиус-вектор точки O, который определяется в 1-м “опыте” (так как точка O — начало координат, то в данном случае ![]() = 0),
= 0), ![]() — радиус-вектор точки A, определяемый во 2-м “опыте”. Имеем
— радиус-вектор точки A, определяемый во 2-м “опыте”. Имеем
![]() , i = 1, ..., N.
, i = 1, ..., N.
Вычитая из левой части этого равенства величину ![]() , а из правой части — равную ей величину
, а из правой части — равную ей величину ![]() , получим соотношение для приращений радиусов-векторов
, получим соотношение для приращений радиусов-векторов
![]() (2.4)
(2.4)
где ![]() ,
, ![]() .
.
Выражение для ![]() определяется аналогично (2.1):
определяется аналогично (2.1):
 .
.
Подставляя в правую часть этого равенства выражение из (2.4), получим
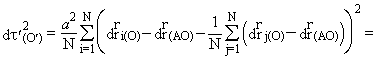
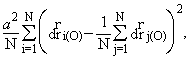
это означает, что
![]() . (2.5)
. (2.5)
Величина ![]() характеризует скорость движения одной системы отсчета относительно другой. Поэтому (2.4) есть преобразование Галилея, которое можно записать в обычном виде:
характеризует скорость движения одной системы отсчета относительно другой. Поэтому (2.4) есть преобразование Галилея, которое можно записать в обычном виде:
![]() . (2.6)
. (2.6)
Таким образом, равенства (2.5) и (2.6) есть традиционные преобразования классической ньютоновой механики. Новым является то, что время t оказывается инвариантным относительно преобразований (2.6), т.е. равенство (2.5) не постулируется, как в стандартной теории, а выводится.
Из галилеевых преобразований (2.5) и (2.6) следует обычное выражение для преобразований скоростей
![]() . (2.7)
. (2.7)
Причем эти преобразования справедливы для всех систем отсчета (по крайней мере, движущихся относительно друг друга поступательно, но не обязательно с постоянной скоростью). Понятие инерциальной системы отсчета пока не определено. Сформулируем критерий инерциальности и соответственно установим связь предложенных математических соотношений с уравнениями движения в механике Ньютона.
§3. Получение уравнений Ньютона в модели
Уравнение (2.1) будет служить основой для получения аналогов законов сохранения и уравнений движения (для данной модели правильней говорить не о законах сохранения, а о равенствах, выражающих сохранение некоторой величины, поскольку теперь эти равенства будут уже не постулируемыми положениями, а следствиями изначального уравнения (2.1)).
Введем условие, определяющее инерциальную систему отсчета. Поскольку в определение модельного времени входят глобальные характеристики всех частиц — в пределе это вся масса Метагалактики, то естественно ожидать, что определение инерциальной, а, следовательно, и неинерциальной системы отсчета соприкасается с принципом Маха, затрагивающего, в частности, связь свойств системы отсчета со свойствами движения тел, которые представляют систему отсчета.
Раскрывая в правой части (2.3) сумму квадратов, получим
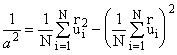 .
.
Выделим группу M частиц, инерционные свойства которой будем изучать. Представим последнее равенство в следующем виде:
 . (3.1)
. (3.1)
Инерционные свойства заданной системы отсчета будут определяться через динамические характеристики N-M частиц (или через свойства M частиц — это традиционный способ определения инерционных свойств системы отсчета). С их помощью и будем формулировать критерий инерциальности системы отсчета. Напомним, что в данной модели система отсчета образуется из “неподвижного тела” — некоторых L частиц (с их помощью задается и система координат) и “подвижного тела” — всей совокупности частиц, движущихся относительно “неподвижного тела”. Ход часов в модели определяется поведением всех частиц, в том числе и частиц “неподвижного тела”, поскольку в сумме (2.1) эти L членов в общем случае дают ненулевой вклад. Характер движения частиц относительно выбранного “неподвижного тела” может быть различным. В зависимости от этого систему отсчета (с отмеченными частицами, выбранными в качестве “неподвижного тела”) можно назвать инерциальной или неинерциальной. Если в качестве “неподвижного тела” выбрана иная система частиц с номерами L+1, ..., L1, то движение рассматриваемых N-M частиц относительно него может быть иным. Соответственно и новая система отсчета может обладать иными свойствами (стать инерциальной или неинерциальной).
Получение из скалярной меры (кинетической энергии) векторной меры движения частиц (импульса) существенно опирается на групповые свойства рассматриваемого уравнения. Как известно, на инвариант непрерывной группы накладываются некоторые условия (являющиеся следствием инвариантности), задаваемые с помощью инфинитезимальных операторов. В данном случае группа — трехпараметрическая (галилеева), поэтому и получаются три уравнения. Если инвариантом является кинетическая энергия, сохраняющаяся во времени, то получаем три уравнения, выражающие собой сохранение во времени импульса выбранной системы частиц. (Отметим, что методологические рассуждения, в которых из скалярной меры движения с привлечением галилеевых преобразований получалась векторная мера, были развиты Сорокиным (1956) и воспроизведены Айзерманом (1974).) В нашем случае принципиальное отличие заключается в том, что галилеевы преобразования не постулируются, а получаются как следствие исходного уравнения (2.1).
Рассмотрим вначале важный пример инерциальной системы отсчета. Таковой будет система отсчета, в которой центр масс всех частиц движется равномерно, т.е. ![]() , где
, где ![]() , такую систему в качестве инерциальной определял еще Мах (1979). Легко видеть, что любая система отсчета, движущаяся с постоянной скоростью относительно указанной, также будет удовлетворять этому условию. Из (3.1) можно заключить, что для данного класса систем отсчета будет постоянна во времени суммарная кинетическая энергия всех частиц. С учетом групповых свойств отсюда следует сохранение суммарного импульса всех частиц (этот вывод можно сделать и на основании того, что центр масс движется с постоянной скоростью). Будем считать теперь, что выделенная система M частиц замкнута, т.е. взаимодействиями ее с другими частицами можно пренебречь. Естественно в этом случае “разделенности” частей мира положить
, такую систему в качестве инерциальной определял еще Мах (1979). Легко видеть, что любая система отсчета, движущаяся с постоянной скоростью относительно указанной, также будет удовлетворять этому условию. Из (3.1) можно заключить, что для данного класса систем отсчета будет постоянна во времени суммарная кинетическая энергия всех частиц. С учетом групповых свойств отсюда следует сохранение суммарного импульса всех частиц (этот вывод можно сделать и на основании того, что центр масс движется с постоянной скоростью). Будем считать теперь, что выделенная система M частиц замкнута, т.е. взаимодействиями ее с другими частицами можно пренебречь. Естественно в этом случае “разделенности” частей мира положить ![]() , где
, где ![]() , и, как тогда следует из (3.1),
, и, как тогда следует из (3.1), ![]() . Так как последнее равенство инвариантно относительно преобразований Галилея (это справедливо для систем отсчета, движущихся с постоянной скоростью относительно данной), то можно записать
. Так как последнее равенство инвариантно относительно преобразований Галилея (это справедливо для систем отсчета, движущихся с постоянной скоростью относительно данной), то можно записать
![]() (3.2)
(3.2)
где инфинитезимальные операторы Xa группы Галилея имеют вид (например, для компоненты скорости u0x):
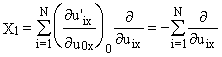 .
.
Применяя эти операторы в (3.2), получим
![]() (3.3)
(3.3)
Умножим обе части (3.3) на me (подчеркнем, что для простейшей модели одинаковых частиц величина массы me не имеет значения, ее можно положить равной, например, массе нуклона). Имеем
![]() , (3.4)
, (3.4)
т.е. суммарный импульс системы M частиц сохраняется. Для общего случая сформулируем следующее условие (критерий) инерциальности выбранной системы отсчета:
![]() . (*)
. (*)
Из условия (*), как легко показать, получаются уравнения (3.3) и соответственно аналог закона сохранения импульса (3.4). Заметим, что в данном общем случае первая сумма в (3.1), являющаяся по сути кинетической энергией системы N частиц, не обязательно сохраняется. из (3.4) не следует еще, что
![]() ,
,
поскольку не всегда выполнено равенство
![]() .
.
Действительно, равенство (3.1) означает, что постоянной является разность между кинетической энергией всех частиц и кинетической энергией движения центра масс всего мира. Каждый из членов в этой разности в принципе может меняться со временем. Если меняется суммарная кинетическая энергия
![]() ,
,
то будет меняться и суммарный импульс системы N частиц (как следует из (3.1)).
Если для системы M = N частиц применить инфинитезимальные операторы Xa, то из (3.1) получим
 ,
,
т.е. имеем тождество
![]()
или в векторном виде
![]() -
- ![]() = 0.
= 0.
Отсюда нельзя сделать заключение о том, сохраняется ли величина ![]() со временем или нет, соответственно и суммарная кинетическая энергия всех частиц может быть постоянной или меняться со временем.
со временем или нет, соответственно и суммарная кинетическая энергия всех частиц может быть постоянной или меняться со временем.
Если приведенные рассуждения о сохранении суммарного импульса (3.4) в инерциальной системе отсчета применить к отдельной частице (M = 1), то получим аналог 1-го закона Ньютона. Пусть M = 2, из (3.4) получим
![]() .
.
Продифференцировав обе части этого равенства по времени, имеем
![]() . (3.5)
. (3.5)
Если назвать выражение в правой части (3.5) силой ![]() , действующей на 1-ю частицу со стороны 2-й (т.е. дать таким образом определение силы), то получим аналог 2-го закона Ньютона.
, действующей на 1-ю частицу со стороны 2-й (т.е. дать таким образом определение силы), то получим аналог 2-го закона Ньютона.
Соответственно называя силой ![]() , действующей на 2-ю частицу со стороны 1-й, величину
, действующей на 2-ю частицу со стороны 1-й, величину ![]() , получим аналог 3-го закона Ньютона.
, получим аналог 3-го закона Ньютона.
Если условие (*) нарушается, т.е. хотя бы одна из компонент вектора ![]() непостоянна, то данная система отсчета не будет инерциальной, поскольку суммарный импульс выбранной группы частиц не сохраняется.
непостоянна, то данная система отсчета не будет инерциальной, поскольку суммарный импульс выбранной группы частиц не сохраняется.
В предлагаемой модели инерциальные свойства вводятся в соответствии (в определенном смысле) с принципом Маха. Представления самого Э.Маха (1979) сформулированы следующим образом: “Вместо того чтобы относить движущееся тело K к пространству (к какой-нибудь координатной системе), будем рассматривать непосредственно его отношение к телам мира, посредством которых только и можно определить систему координат”. Если условие (*) выполнено, то определена инерциальная система отсчета (причем, как легко видеть, одна инерциальная система отсчета может двигаться относительно другой только с постоянной скоростью). В случае нарушения условия (*) данной моделью описываются, по крайней мере, все неинерциальные системы отсчета, движущиеся относительно инерциальных поступательно и ускоренно. Рассмотрим для примера систему отсчета, скорость которой относительно некоторой инерциальной системы равна ![]() (t), причем
(t), причем ![]() . Пусть M = 1. В инерциальной системе отсчета выделенная 1-я частица движется с постоянной скоростью, т.е.
. Пусть M = 1. В инерциальной системе отсчета выделенная 1-я частица движется с постоянной скоростью, т.е. ![]() = const.
= const.
Преобразования (2.7) справедливы и в рассматриваемом случае, учитывая их, получим для значения ускорения 1-й частицы в ускоренной системе отсчета
![]() ,
,
т.е. 1-й закон Ньютона нарушается (естественно, что условие (*) не выполняется в указанном случае, иначе получилось бы, что ![]() ).
).
Запишем вид силы инерции для рассматриваемого случая. Продифференцировав по времени все члены в равенстве
![]() ,
,
получим
![]() .
.
Величину, стоящую в правой части последнего равенства, можно отождествить с воздействием всех частиц системы на 1-ю частицу, т.е. с силой инерции, действующей на эту частицу в неинерциальной системе отсчета. Так трактуется принцип Маха в рамках рассматриваемой модели. Здесь он пока формулируется на уровне уравнений движения, дальнейшее развитие данных представлений требует, естественно, введения закона для силы, зависящей от расстояния, для чего надо будет построить модель пространства (масштабных линеек).
§4. Принцип соответствия и эффекты, связанные
с конечностью числа частиц N
Необходимо определить, каким образом введенная математическая модель часов (время t) соотносится с реальными физическими часами, т.е. с прибором, с помощью которого производятся измерения в обычной физической модели (время tc). Будем полагать, что заданы N векторных случайных процессов (например, однородных с независимыми приращениями), которые моделируют величины ![]() (i = 1, ..., N) с учетом характера получения “фотографий”. Тогда
(i = 1, ..., N) с учетом характера получения “фотографий”. Тогда  также являются случайными величинами. Будем полагать, что для “идеальных физических часов”, по которым определяется время tc, должно выполняться соотношение
также являются случайными величинами. Будем полагать, что для “идеальных физических часов”, по которым определяется время tc, должно выполняться соотношение
![]() , (4.1)
, (4.1)
где MO обозначает математическое ожидание случайной величины dt2, которая определяется из (2.1), поэтому более подробно это равенство переписывается так:
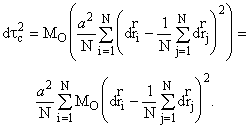
Смысл введения такого выражения для dtc заключается в следующем. Можно предположить, что ход реальных часов устанавливался путем создания все более точных эталонов времени, получаемых сравнением хода часов с движением большого числа астрономических и других объектов. Об этом подробнее будет сказано в §6. Осредненной таким образом величине hi можно поставить в соответствие ![]() , а для всех частиц
, а для всех частиц ![]() .
.
Пусть независимые случайные величины ![]() имеют конечные дисперсии (они одинаково распределены). Тогда в условиях выполнения предельной теоремы (см. это выражение, например, в книге Б.В.Гнеденко (1961)):
имеют конечные дисперсии (они одинаково распределены). Тогда в условиях выполнения предельной теоремы (см. это выражение, например, в книге Б.В.Гнеденко (1961)):
 ,
,
где дисперсия ![]() . Если ее считать порядка величины dt2, то получим
. Если ее считать порядка величины dt2, то получим
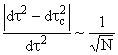 . (4.2)
. (4.2)
Реальные конкретные физические часы могут, конечно, отличаться в своих показаниях от “идеальных физических часов”, которые дают показания, близкие к dt согласно (4.1) (в рамках принятой вероятностной модели). Это означает, что с помощью какого-нибудь типа часов, например, атомных, могут быть получены отклонения большие, но во всяком случае, не меньшие, чем O![]() .
.
При N ® Ґ величина dtc стремится к dt по вероятности. Тогда все соотношения классической теории выполняются точно. Так устанавливается принцип соответствия в модели.
Важно подчеркнуть, что получающиеся из (2.1) уравнения (в них пока фигурирует величина dt) являются, по сути, следствием математических аксиом, которые позволяют совершать различные операции над величинами в (2.1) (коммутативный, ассоциативный и другие математические законы). Формула (2.1) дает возможность уменьшить число независимых физических размерных величин на единицу, поскольку время измеряется здесь через пространственные величины. Сведение уравнений к безразмерному виду и позволяет высказать важное предположение, что в основе нашего знания о мире лежат математические соотношения, а физический смысл им придается, если подставляются вместо математических формальных величин некоторые физически измеримые значения.
Применительно к уравнению (2.1) это соответствует тому, что вместо dt должна быть подставлена физически измеримая величина dtc. Но после такой подстановки окажется, что уравнения движения, соответствующие аналогичным уравнениям в ньютоновой механике, выполняются с точностью до O![]() . Этот факт может служить основой для получения наблюдаемых эффектов, которые отличают данную теорию от традиционной. Указанные отклонения, правда, лежат далеко за пределами возможностей современных приборов (при N ~ 1080 оказывается
. Этот факт может служить основой для получения наблюдаемых эффектов, которые отличают данную теорию от традиционной. Указанные отклонения, правда, лежат далеко за пределами возможностей современных приборов (при N ~ 1080 оказывается ![]() ~ 10-40).
~ 10-40).
Наличие указанных отклонений можно сопоставить с предположениями работы Дж.Лоренса и Г.Замоси (L.K.Lawrence, G.Szamosi, 1974), где для получения известной связи между фундаментальными константами выдвигается гипотеза о том, что физические параметры частиц одного класса (например, массы) образуют статистическое распределение, зависящее от общих тепловых свойств Вселенной (флуктуации порядка ![]() ), отсюда можно заключить, что две элементарные частицы двигаются (в одинаковых условиях), отличаясь в своих кинематических характеристиках на величину такого же порядка.
), отсюда можно заключить, что две элементарные частицы двигаются (в одинаковых условиях), отличаясь в своих кинематических характеристиках на величину такого же порядка.
Отметим, что в проекте “фундаментальной теории” (Эддингтон, 1949) все расстояния определяются с точностью не выше, чем ![]() . Следовательно, и здесь уравнения содержат флуктуации такого же порядка.
. Следовательно, и здесь уравнения содержат флуктуации такого же порядка.
§5. Построение релятивистского обобщения модели
До сих пор модель была ограничена предположением о существовании единого сигнала (света), охватывающего весь мир, что позволяло получать в пространственно-разделенных точках идентичные “фотографии”. Будем рассматривать более общую ситуацию, когда в пространственно-разделенных точках нельзя получить полностью идентичные “фотографии”, в этих условиях и будем получать зависимости между величинами, которые характерны для специальной теории относительности (СТО). Эта ситуация более сложна для анализа, поскольку пространственно-разделенные “фотографии”, даже связанные световым лучом, выпущенным из первой точки во вторую, будут давать одинаковые положения только для частиц, также связанных именно этим лучом. Другие световые лучи, пришедшие во вторую точку, принесут другую информацию, чем лучи, пришедшие в первую точку. Поэтому теперь нельзя, как при выводе формулы (2.4), считать, что будет равенство для вторых “опытов”, полученных в различных пространственных точках. Это означает, что в общем случае
![]()
и соответственно ![]() теперь нельзя заменить на
теперь нельзя заменить на ![]() . Таким образом, теперь нельзя ввести единое время, поскольку
. Таким образом, теперь нельзя ввести единое время, поскольку ![]() не равно
не равно ![]() , но можно попытаться построить модель собственного времени (в духе вышеприведенного высказывания Паули), которая позволяла бы получать инвариантное значение в различных системах отсчета, а затем на его основе найти обобщение модельного времени, принятого в СТО.
, но можно попытаться построить модель собственного времени (в духе вышеприведенного высказывания Паули), которая позволяла бы получать инвариантное значение в различных системах отсчета, а затем на его основе найти обобщение модельного времени, принятого в СТО.
Будем использовать те же обозначения, что и в §2. Собственное время в “штрихованной” системе задается обычным образом
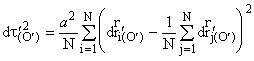 . (5.1)
. (5.1)
С помощью величин ![]() , измеренных в собственной системе отсчета, будем определять некие величины dri(OA) по следующей формуле:
, измеренных в собственной системе отсчета, будем определять некие величины dri(OA) по следующей формуле:
![]() (5.2)
(5.2)
Эти величины отнесены к точкам O и A, поскольку, по крайней мере для точки A (которой соответствует Oґ в “штрихованной” системе), величина ![]() может быть определена по двум “фотографиям”, соответствующим 1-му “опыту” в точке O и 2-му “опыту” в точке A (действительно,
может быть определена по двум “фотографиям”, соответствующим 1-му “опыту” в точке O и 2-му “опыту” в точке A (действительно, ![]() ). Другие величины
). Другие величины ![]() , определяемые из (5.1), не могут быть в общем случае измерены по разности двух “опытов” в O и A. В самом деле, при фотографировании неподвижного и движущегося объекта получаются различные образы, поэтому соотношение между координатами частиц в “опытах”, полученных в движущихся относительно друг друга системах отсчета, не может иметь характер простого сдвига (5.1) (вопросу видимой формы движущихся объектов посвящена обширная литература, см., например, один из последних обзоров (Болотовский, 1990)).
, определяемые из (5.1), не могут быть в общем случае измерены по разности двух “опытов” в O и A. В самом деле, при фотографировании неподвижного и движущегося объекта получаются различные образы, поэтому соотношение между координатами частиц в “опытах”, полученных в движущихся относительно друг друга системах отсчета, не может иметь характер простого сдвига (5.1) (вопросу видимой формы движущихся объектов посвящена обширная литература, см., например, один из последних обзоров (Болотовский, 1990)).
Образуем из ![]() величину, аналогичную модельному времени
величину, аналогичную модельному времени
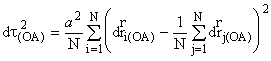 . (5.3)
. (5.3)
Из (5.2) следует
![]() . (5.4)
. (5.4)
Определим теперь время ![]() , прошедшее между двумя событиями, первое из которых заключается в пролете точки Oґ мимо точки O, а второе — в пролете точки Oґ мимо точки A (будем сопоставлять вводимый временноў й интервал с аналогичной величиной в СТО):
, прошедшее между двумя событиями, первое из которых заключается в пролете точки Oґ мимо точки O, а второе — в пролете точки Oґ мимо точки A (будем сопоставлять вводимый временноў й интервал с аналогичной величиной в СТО):
 . (5.5)
. (5.5)
Для каждого слагаемого в данной статистической сумме добавлен член, учитывающий “запаздывание”, — оно должно проявиться и для макроскопической величины. Раскрывая квадраты и проводя суммирование в правой части (5.5), имеем
![]() . (5.6)
. (5.6)
переписывая (5.6), получим знакомое выражение из СТО для собственного времени
![]() . (5.7)
. (5.7)
Можно получить ограничение на скорость частицы уже из (5.6) (для описания движения частицы мы можем связать с ней начало отсчета Oґ “штрихованной” системы, скорость частицы определяется естественным образом ![]() ):
):
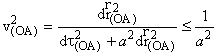 . (5.8)
. (5.8)
Величину, ограничивающую скорость частицы, можно сопоставить со скоростью света в вакууме c, т.е. a = 1/c.
Предельное значение 1/a достигается, когда ![]() = 0 или скорость
= 0 или скорость ![]() , которая определяется, как и раньше:
, которая определяется, как и раньше: ![]() , стремится к бесконечности.
, стремится к бесконечности.
Отметим, что, как следует из основного уравнения (2.1) (или аналогичного уравнения (5.1)), величина c, т.е. 1/a, имеет смысл среднеквадратичной скорости всех частиц мира, определяемой при “фотографировании” из одной точки (см. (2.3)). Это не противоречит теории относительности. Промежуток времени ![]() , и это соответствует теории относительности, определяется посредством измерения в двух различных точках. Синхронизация аналогична синхронизации по Эйнштейну, что следует из (5.6). Как известно, собственная скорость в СТО (определяемая с помощью собственного времени) может быть неограниченно большой, она стремится к бесконечности, когда скорость, определяемая по
, и это соответствует теории относительности, определяется посредством измерения в двух различных точках. Синхронизация аналогична синхронизации по Эйнштейну, что следует из (5.6). Как известно, собственная скорость в СТО (определяемая с помощью собственного времени) может быть неограниченно большой, она стремится к бесконечности, когда скорость, определяемая по ![]() , стремится к c. Величина скорости, определяемая по модельным часам с помощью “фотоаппарата”, находящегося в одной точке, также может быть сколь угодно большой, поэтому неудивительно, что средняя скорость в этом случае равна c.
, стремится к c. Величина скорости, определяемая по модельным часам с помощью “фотоаппарата”, находящегося в одной точке, также может быть сколь угодно большой, поэтому неудивительно, что средняя скорость в этом случае равна c.
Связь между ![]() и
и ![]() аналогична соотношению между обычной и собственной скоростью в СТО:
аналогична соотношению между обычной и собственной скоростью в СТО:
![]() .
.
Отметим, что время из (5.5) переходит в модельное время, задаваемое формулой (2.1), если А стремится к О, т.е. если частица, с которой мы связываем собственную систему отсчета, неподвижна. Аналогично ![]() . Из (5.7) следует
. Из (5.7) следует
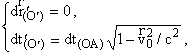 (5.9)
(5.9)
что соответствует частному случаю преобразований Лоренца. Подчеркнем, что в отличие от преобразований Галилея (получавшихся в §2), справедливых для всех частиц мира, преобразование Лоренца (5.9) справедливо только для одной рассматриваемой частицы. Эта частица находилась ко второму “опыту”, полученному в собственной системе отсчета в точке Oґ, в точке A. Время ![]() и вводится только для одной этой точки. Другие
и вводится только для одной этой точки. Другие ![]() (как указывалось, они не определяются по “опытам” в O и A, а находятся из величин “опытов” в точке Oґ) не связаны лоренцевым соотношением с
(как указывалось, они не определяются по “опытам” в O и A, а находятся из величин “опытов” в точке Oґ) не связаны лоренцевым соотношением с ![]() , поэтому не возникает противоречия с “галилееподобным” преобразованием (5.1).
, поэтому не возникает противоречия с “галилееподобным” преобразованием (5.1).
Преобразований (5.9) достаточно для вывода уравнений релятивистской динамики, однако рассмотрим вначале получение преобразований Лоренца в общем случае.
Пусть, как и ранее, 1-е событие состоит в пролете частицы мимо начала отсчета O, 2-е событие состоит в пролете данной частицы мимо некоторой точки B. Но теперь этой точке будет соответствовать некоторая точка Bґ, не совпадающая с началом отсчета Oґ “штрихованной” системы. Свяжем с рассматриваемой частицей начало отсчета OІ собственной (сопутствующей) системы отсчета. Собственное время для этой точки записывается аналогично (5.1):
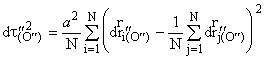 . (5.10)
. (5.10)
С помощью величин ![]() , измеренных по двум “опытам” в этой системе отсчета, определим величины
, измеренных по двум “опытам” в этой системе отсчета, определим величины ![]() и
и ![]() для “штрихованной” и “лабораторной” систем по аналогии с (5.2):
для “штрихованной” и “лабораторной” систем по аналогии с (5.2):
![]()
![]() (5.11)
(5.11)
Теперь вводим величины
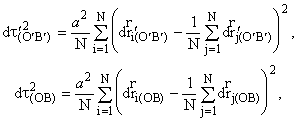
как следует из (5.11), они равны величине интервала времени (5.10)
![]()
Определяя величину релятивистского времени аналогично (5.5):

получим окончательное соотношение
![]()
Отсюда, если, как обычно, предположить линейную зависимость величин ![]() и
и ![]() от dt(OB) и dx(OB), то получим преобразования Лоренца в общем случае.
от dt(OB) и dx(OB), то получим преобразования Лоренца в общем случае.
Уравнения движения с использованием инвариантного времени получаются таким же образом, как и в §3; так как вид зависимости в определении этого времени в (5.3) полностью соответствует зависимости в основной формуле (2.1), то уравнения движения также будут соответствовать полученным ранее. Например, для некоторой (1-й) частицы имеем
![]() . (5.12)
. (5.12)
Этот вид уравнения в инвариантной форме, принятой в СТО. В правой части (5.12) стоит трехмерная часть от 4-вектора силы Минковского (Паули, 1983). Для перехода к ньютоновой силе (в релятивистском обобщении) заменим dt через dt согласно (5.9), получим
 ,
,
где 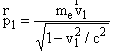 — релятивистский импульс частицы. В обычном виде уравнение движения записывается следующим образом:
— релятивистский импульс частицы. В обычном виде уравнение движения записывается следующим образом:
![]() ,
,
где ньютонова сила связана с силой Минковского уравнением ![]() .
.
Определяя работу обычным образом, получим из (5.12) выражение для релятивистской энергии.
Таким образом, в модели получаются релятивистские динамические уравнения. Отличия от стандартной теории, связанные со статистичностью модели, могут проявиться при очень большой скорости частицы. При этом вклад этой частицы в основную сумму в (2.1) оказывается столь большим, что нарушаются условия выполнения предельной теоремы, и для выполнения условия типа (4.1) надо отделить член в сумме, который задает рассматриваемая частица. Это приводит к некоторому изменению в уравнениях движения. Не приводя выкладок, лишь отметим, что отличия от традиционных уравнений могут проявиться, когда скорость частицы станет равной по порядку величине ![]() . Если N~1080, то данное значение скорости на много порядков превышает максимальные скорости элементарных частиц, достигнутых в современных ускорителях.
. Если N~1080, то данное значение скорости на много порядков превышает максимальные скорости элементарных частиц, достигнутых в современных ускорителях.
Отличия, связанные со статистическим характером данной модели, могут проявиться при конечном N. Строго говоря, заключение о конечности массы Метагалактики можно сделать лишь после построения модели замкнутого мира в рамках общей теории относительности (это должно быть сделано на следующем этапе развития последовательной реляционной теории пространства-времени в данной модели, что связано, в частности, с построением модели масштабных линеек). Но статистические эффекты указанных порядков должны, по нашему мнению, проявляться на разных уровнях будущих построений, это связано с необходимостью объяснения больших чисел в так называемых космологических совпадениях. Важными в этом смысле представляются следующие слова Г.Вейля (1984): “Постулат Маха все еще ждет своей теории (не будет ли это статистическая теория гравитации, на которую вроде бы указывает квадратный корень в законе ![]() )?”. В этих рассуждениях вводится предполагаемая связь между e — отношением констант гравитационного и электромагнитного взаимодействия и числом частиц в мире N.
)?”. В этих рассуждениях вводится предполагаемая связь между e — отношением констант гравитационного и электромагнитного взаимодействия и числом частиц в мире N.
§6. Свойства модельного времени и возможные обобщения
До сих пор речь шла в основном о метрических свойствах времени, определяемых предложенной моделью часов (фактически рассматривался темп мировых часов), именно эти свойства были важны для получения соотношений традиционной схемы механики и некоторых отличий от нее. Однако можно заметить, что данная модель обладает “избыточностью”, позволяющей более подробно по сравнению со стандартной описывать свойства времени. Действительно, в результате 3N-параметризации времени в конфигурационном пространстве обретает смысл понятие “мгновение”, в котором заложена информация о пространственном положении всех частиц мира. Это позволяет более определенно поставить вопрос о некоторых свойствах времени. В данном параграфе и будут изучаться общие черты предлагаемой конструкции времени, а также рассматриваться возможные перспективы усовершенствования модели.
Здесь не будут обсуждаться многочисленные философские проблемы, связанные с категорией времени. Можно заметить только, что данное модельное время связано с более широким понятием “движение”, онтологическая основа такого времени лежит в первичной возможности различения оппозиции “субъект — объект”. Вопрос о происхождении движения в мире здесь не рассматривается.
Остановимся кратко на возможности фиксирования в модели самого движения частиц и тем самым элементов длительности, из которой и строится промежуток времени. Проблема “теперь” подробно обсуждалась еще в “Физике” Аристотеля (1981): “Одна часть его была, и ее уже нет, другая будет, и ее еще нет; из этих частей слагается и бесконечное время, и каждый раз выделяемый промежуток времени. А то, что слагается из несуществующего, не может, как кажется, быть причастным существованию. Кроме того, для всякой делимой вещи, если только она существует, необходимо, чтобы, пока она существует, существовали бы или все ее части, или некоторые, а у времени, которое также делимо, одни части уже были, другие — будут, и ничто не существует. А “теперь” не есть часть, так как часть измеряет целое, которое должно слагаться из частей; время же, по всей видимости, не слагается из “теперь”.” В предлагаемой модели “теперь”, т.е. “мгновенье”, действительно, чисто пространственно, оно не содержит еще временноў й характеристики. Время слагается из малых промежутков, которые определяются из разностей “теперь”. Для этого использовались, как указывалось, пары “фотографий”. Можно отметить, однако, что в силу конечности “выдержки” на “фотографии” можно фиксировать, по-видимому, не только радиусы-векторы ![]() всех частиц, но и их малые приращения
всех частиц, но и их малые приращения ![]() (все частицы будут на “фотографиях” выглядеть несколько “смазанными”). Тем самым будут фиксироваться следы, “мазки”, отпечатки движений частиц. Начало и конец векторов приращений
(все частицы будут на “фотографиях” выглядеть несколько “смазанными”). Тем самым будут фиксироваться следы, “мазки”, отпечатки движений частиц. Начало и конец векторов приращений ![]() можно зафиксировать некоторым способом, поскольку есть различие в открывании и закрывании “объектива фотоаппарата” (включая при открывании и закрывании нужные световые фильтры, можно добиться того, чтобы начала векторов приращений
можно зафиксировать некоторым способом, поскольку есть различие в открывании и закрывании “объектива фотоаппарата” (включая при открывании и закрывании нужные световые фильтры, можно добиться того, чтобы начала векторов приращений ![]() получались на “фотографиях”, например, зелеными, а концы — синими).
получались на “фотографиях”, например, зелеными, а концы — синими).
6.2. Описание течения времени и вопрос об “обратимом времени”
В определении величины dt, которое дается в формуле (2.1), вопрос о направлении времени не ставился. Характерно, что в (2.1) входят квадратичные величины, это означает, что порядок следования “опытов” здесь не имеет значения. Важна только величина расстояния (в 3N-мерном конфигурационном пространстве) между двумя “опытами”. Оказывается, что данных метрических соотношений достаточно для получения уравнений классической механики, обратимых во времени.
Для того чтобы подойти к тому, как может пониматься “необратимость” времени в модели (и соответственно его “обратимость”, но в более общем смысле, чем это принято понимать в механике), необходимо рассмотреть вопрос об описании течения времени. Для этого можно использовать несколько более сложный прибор — “фотоаппарат с памятью”, т.е. к “фотоаппарату” присоединяется некоторое запоминающее устройство, в котором фиксируется вся последовательность полученных “опытов” (отметим, что многими философами понятие памяти выдвигается в качестве необходимого условия для формирования понятия времени).
Рассмотрим процесс описания течения времени с помощью такого прибора. Вначале в “памяти” ничего не зафиксировано. Получаем некоторый “опыт” и соответственно запоминаем набор радиусов-векторов всех частиц. Этому “опыту” присваивается номер 1. Получаем значение некоторого другого “опыта”, причем значения всех радиусов-векторов отличаются от соответствующих значений в “опыте номер 1” на дифференциально-малые величины. Новому “опыту”, который фиксируется в “памяти”, присваивается номер 2 и т.д.
Принципиально, что здесь не ставится вопрос о том, имеется ли заданная “изначально” последовательность моментов времени, т.е. подразумеваются ли заложенными некоторые свойства времени. Важно, что дается способ описания смены “мгновений”, который операционально достаточен для моделирования интуитивно понимаемого течения времени и описания последовательности моментов времени с помощью обычных часов. В рамках предлагаемой модели момент времени полностью определяется “опытом”. Указанным выше образом “опытам” будет поставлена в соответствие некоторая возрастающая последовательность целых чисел (этот процесс аналогичен до некоторой степени тому, как изменяющимся в нашем визуальном пространстве образам зримого мира ставится в соответствие некоторая возрастающая последовательность чисел в электронных часах). Эту последовательность (“опытов” и целых чисел) и можно связать с направлением времени. (Все данные в этом абзаце апелляции к аналогии измерения времени по обычным часам с теоретической точки зрения фактически нужны для того, чтобы перейти к некоторой “аксиоме измерения” в рассматриваемой модели, которая соответствует процессу установления последовательности моментов времени в модели.)
Понимание “необратимости” времени в данной расширенной модельной формулировке связано с тем, что различные “опыты” отличаются друг от друга. Если считать, что частицы перемещаются некоторым случайным образом, то вероятность совпадения двух различных “опытов” чрезвычайно мала. Теоретически можно представить ситуацию, что некоторый “опыт” совпадет с другим из полученной последовательности. В такой ситуации можно было бы считать, что время “вернулось назад”, хотя, суммируя положительные величины из формулы (2.1), мы получали бы конечное значение времени, прошедшего между этими “опытами”. Такую ситуацию и можно было бы связать с “обратимостью” времени (противоположной “необратимости” в указанном выше смысле). В математической формулировке такое более сложное время должно было бы описываться так, что при обнаруженной “обратимости” отсчет можно было бы начать с прежней отметки (с “динамической точки зрения” два состояния мира надо было бы считать полностью идентичными, если кроме совпадения всех радиусов-векторов имело бы место совпадение и всех скоростей частиц). Обычное “житейское” ощущение необратимости времени связано с пониманием того, что “что-то меняется” в мире по сравнению с тем, что было раньше; рассматриваемая модель, принимая атомарную гипотезу, формализует это знакомое всем ощущение с помощью фиксации изменения “опытов”.
6.3. Обобщение понятия времени для различных систем частиц
В предыдущих параграфах число частиц полагалось равным максимально большому в мире (переход к точным уравнениям механики происходит при стремлении этого числа к бесконечности). Однако аналогичные построения можно провести и для различного числа частиц.
Минимальное число, для которого формула (2.1) имеет смысл, равно 2. Для одной частицы (если вообще можно представить себе такой вырожденный случай, который характеризует “неразделенный” мир) время не течет, поскольку с единственной частицей должна быть связана система отсчета.
Можно вводить по аналогии с (2.1) “внутреннее время” системы N1 частиц. Если число частиц в системе мало, то можно влиять, воздействовать на движение частиц, в этом случае “время” такого микрокосма является в определенным смысле управляемым (“рукотворным”). Множитель a2, который стоит в (2.1), описывает термодинамические свойства мира в целом (N частиц). Для системы из меньшего числа частиц N1 можно использовать другой множитель ![]() , характеризующий термодинамические свойства именно этой системы (легко видеть, что он равен массе частицы, деленной на температуру системы). Можно поэтому описать “времена” для различных систем, содержащих различное число частиц N1, N2, ... и построить иерархию “внутренних времен” (как бы вложенных друг в друга), причем предельно общей шкалой будет являться шкала, задаваемая “мировым временем” с предельно большим числом частиц.
, характеризующий термодинамические свойства именно этой системы (легко видеть, что он равен массе частицы, деленной на температуру системы). Можно поэтому описать “времена” для различных систем, содержащих различное число частиц N1, N2, ... и построить иерархию “внутренних времен” (как бы вложенных друг в друга), причем предельно общей шкалой будет являться шкала, задаваемая “мировым временем” с предельно большим числом частиц.
В некоторых физических ситуациях, по-видимому, более удобным при сравнении “внутренних времен” различных систем частиц может быть использование одного и того же множителя a2 из “мирового времени”.
Можно попытаться приложить понятие данного физического времени к системам, где естественно было бы вводить биологическое, географическое, геологическое время и т.д. Для этого надо выделить в рассматриваемой системе некоторые “частицы”, наблюдение за которыми позволяло бы судить о движении. Затем можно ввести “внутреннее время” описанным выше способом, соответствующие часы которого служили бы мерой движения именно для этой системы.
Интерес представляет возможность обобщить модель времени на случай неравновесных систем таким образом, чтобы не было приращения времени в случае теплового равновесия системы. То есть при максимуме энтропии в некоторой системе такое “неравновесное время” остановилось бы, что соответствует взглядам некоторых исследователей (например, В.И.Вернадского) на природу времени, считающих, что имеет смысл вводить время только для неравновесных систем. (Подчеркнем, что и в этом случае приращение времени, задаваемое формулой (2.1), не равнялось бы нулю.) Формула (2.1) не учитывает специфичность неравновесной системы, множитель a2 связан с температурой, однако в неравновесном случае нет полной однородности системы. Для указанного возможного обобщения в рассматриваемой неравновесной системе выделим p групп частиц, которые соответствуют физическим частям системы, поддерживающимся примерно в однородных условиях (это существенное предположение в данном построении). Пусть общее число частиц в системе равно N. Имеем
![]() ,
,
причем будем полагать, что каждая группа частиц достаточно представительна, чтобы проводить осреднение для получения в ней “внутреннего времени” с небольшими флуктуациями. Определим интервал “неравновесного времени” следующим образом:
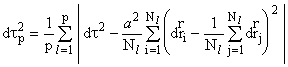 ,
,
где dt2 определяется для системы N частиц по формуле (2.1). Смысл такого интервала “неравновесного времени” заключается в том, что здесь осредняется отклонение некоторой характерной величины (для каждой однородной части) от этой же величины (для всей системы). Оказывается, что в неравновесном состоянии ![]() при переходе к равновесию отдельные достаточно большие части системы имеют примерно одинаковые физические характеристики, поэтому в равновесии
при переходе к равновесию отдельные достаточно большие части системы имеют примерно одинаковые физические характеристики, поэтому в равновесии ![]() , т.е. величина
, т.е. величина ![]() качественно соотносится с H-функцией Больцмана. Поиск более сложной связи с движением в “неравновесном времени” по сравнению с тем, как это задается в (2.1), представляется важным. На этом пути, по-видимому, надо привлечь вышеизложенные соображения о построении “необратимого” времени. Результатом такой конструкции могло бы стать получение некоего фундаментального “необратимого во времени” уравнения (типа кинетического уравнения Больцмана).
качественно соотносится с H-функцией Больцмана. Поиск более сложной связи с движением в “неравновесном времени” по сравнению с тем, как это задается в (2.1), представляется важным. На этом пути, по-видимому, надо привлечь вышеизложенные соображения о построении “необратимого” времени. Результатом такой конструкции могло бы стать получение некоего фундаментального “необратимого во времени” уравнения (типа кинетического уравнения Больцмана).
6.4. О моделировании равномерности времени
Представление о том, что уравнение (2.1) способно моделировать равномерность времени, основывалось на интуитивных соображениях. Постараемся более четко понять, почему осреднение по ансамблю частиц системы позволяет, в принципе, описать равномерность времени.
Само понятие “равномерность” нуждается в некоторых пояснениях. Рейхенбах замечает (Рейхенбах,1985), что, как и для пространственных величин, для времени должна быть использована идея координатной дефиниции: “Первая координатная дефиниция относится к единице длины, вторая — к конгруэнтности. Вопрос о том, равны ли два удаленных друг от друга линейных отрезка, есть вопрос не познания, а определения, и это определение в конечном счете сводится к соотнесению некоторого физического объекта и единицы измерения... проблема конгруэнтности временныў х интервалов приводит к проблеме равномерности времени”. Одно из возможных независимых определений равномерности времени по Рейхенбаху дается с помощью законов механики. Рассматриваемая модель соответствует данному определению, поскольку здесь конструируется такое время, в котором законы движения, в частности закон инерции, являются следствием построений. Другое определение равномерности дается с помощью естественных часов.
Проблему равномерности естественных часов можно попытаться трактовать следующим образом. Как уже указывалось, представляется, что ход часов совершенствовался на протяжении длительного исторического времени, это усовершенствование происходило и в смысле достижения все большей равномерности. Промежутки времени, определяемые по движению Луны, Солнца, других объектов, постоянно совершенствовались. Известен термин “уравнение времени”, возможно, точнее этот процесс было бы назвать “уравнивание времени”, поскольку происходило уточнение хода часов путем сравнения их с движением астрономических объектов. Ход реальных часов устанавливался путем создания все более точных (в определенном смысле) эталонов времени. Выработка эталонного хода часов происходила длительно с помощью некоторого осреднения, по сути дела, по “опытам”; можно сказать, что темп часов постепенно подстраивался под ход всей множественной системы объектов мира (путем сравнения “временныў х” шкал систем и частиц).
В рамках рассматриваемой модели подобные представления можно пояснить на следующем простейшем примере. Будем считать, что N частиц движутся независимо, но реализуют одну и ту же случайную величину (реализация этой случайной величины для i-й частицы ![]() , следуя ранее введенному обозначению, есть
, следуя ранее введенному обозначению, есть 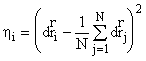 ). По закону больших чисел среднее по реализациям стремится к математическому ожиданию при увеличении числа реализаций:
). По закону больших чисел среднее по реализациям стремится к математическому ожиданию при увеличении числа реализаций:
![]() ,
,
здесь n обозначает номер случайного испытания. Имеется в виду любая случайная величина ![]() , обозначенная через h. В данном простейшем примере среднее от N случайных величин
, обозначенная через h. В данном простейшем примере среднее от N случайных величин ![]() можно рассматривать как осреднение по большому числу реализаций одной случайной величины. Если удастся построить прибор (часы), который подстраивался бы под средний ход часов частиц, а в данном примере — под средний ход (движение) по реализациям даже одной частицы, то можно в этом смысле получить равномерное течение времени, т.е. всегда воспроизводить величину MO(h). Но эту среднюю за большой отрезок времени величину можно моделировать с помощью формулы (2.1) в каждый момент времени; действительно, в обозначениях, принятых в §4, имеем
можно рассматривать как осреднение по большому числу реализаций одной случайной величины. Если удастся построить прибор (часы), который подстраивался бы под средний ход часов частиц, а в данном примере — под средний ход (движение) по реализациям даже одной частицы, то можно в этом смысле получить равномерное течение времени, т.е. всегда воспроизводить величину MO(h). Но эту среднюю за большой отрезок времени величину можно моделировать с помощью формулы (2.1) в каждый момент времени; действительно, в обозначениях, принятых в §4, имеем

Это равенство выполняется с точностью O(![]() ).
).
Данные рассуждения имеют определенный недостаток, поскольку здесь производятся операции с “ненормированными” величинами h(l), “нормировка” означала бы переход к соответствующим скоростям, для этих случайных величин надо было бы провести аналогичные выкладки.
6.5. Свойства модельного времени и возможное развитие модели
Рассмотрим в заключение некоторые общие свойства времени, определяемые на основе введенной модели часов. Это время реляционное, динамическое, конвенциальное и универсальное. Но можно строить “внутреннее время” для любой системы с числом частиц меньшим, чем предельное. Время непрерывно, поскольку пока координаты всех частиц описываются классическим образом — с помощью континуального пространства. Так как время определяется согласно формуле (2.1), то оно одномерно. Однако, в принципе, допустимы и другие, более подробные меры движения. Можно сказать, что в пределе время как характеристика изменений, происходящих в мире, в рамках модели может определяться изменениями всех 3N координат частиц, т.е. в этом смысле время 3N-мерно.
Отметим кратко направления, в которых может быть развита изучаемая модель. Математическое выражение для интервала времени в (2.1) искалось таким образом, чтобы удовлетворить динамическому поведению существующих приборов — часов и соответственно традиционным уравнениям движения. Но можно предложить иной математический вид интервала в формуле, аналогичной (2.1), в которой, например, величины приращений для радиусов-векторов входили бы с весовыми множителями, зависящими от расстояний между частицами и прибором, т.е. “фотоаппаратом”. Для того чтобы придать физический смысл таким построениям, необходимо создать новые часы, которые позволяли бы осреднять движения частиц согласно новой формуле для интервала времени из модифицированного равенства (2.1). Тогда уравнения движения будут иметь также иной вид, где временнаґя переменная будет приобретать физический смысл только при сопоставлении ее с измерением по новым часам. Проблема возможности обобщения модели лежит, таким образом, на пути построения возможных новых приборов как новых способов интеграции движения. (В этом смысле интересно представить себе гипотетическую дисциплину: “физическую математику”.) Введение новых временныў х характеристик может позволить более подробно и полно описывать реальность.
Литература
Айзерман А.И. Классическая механика. М., 1974. С.46-47.
Аристотель. Физика. т.1-4. М., 1981. Т.3. С.145-146.
Болотовский Б.М. О видимой форме движущегося тела // Эйнштейновский сборник. 1986-1990. М., 1990. С. 279-328.
Вейль Г. Основные черты физического мира. Форма и эволюция // Избранные труды. Математика. Теоретическая физика. М., 1984. С.349.
Гнеденко Б.В. Курс теории вероятностей. М., 1961.
Мах Э. Механика. Историко-критический очерк ее развития // Альберт Эйнштейн и теория гравитации. М., 1979. С.57.
Паули В. Физические очерки. М., 1975. С.422-423.
Паули В. Теория относительности. М., 1983.
Пуанкаре А. Последние мысли // О науке. М., 1983. С.422-423.
Рейхенбах Г. Философия пространства и времени. М., 1985. С.133-134.
Сорокин В.С. Законы сохранения и мера движения в физике // Успехи физических наук. 1956. Т.IX, вып.2. С.325-362.
Эйнштейн А. Автобиографические заметки // Собр. научн. трудов. М., 1967. Т.1. С.280-281.
Eddington A. Fundamental theory. Cambridge, 1949.
Lawrence J.K., Szamosi G. Statistical physics, particle masses and the cosmological considenses // Nature. 1974. V.252. P.538-539.
Zimmermann E.J. The macroscopic nature of space-time // American Journ. of Physics. 1962. V.30, №2. P.97-105.