Андрей ГАЛАКТИОНОВ

ПРИРОДА
НЕОБРАТИМОСТИ

Почему мы можем свободно перемещаться в пространстве вперед и назад, а время неумолимо бежит только в одну сторону? Оказывается, все дело во взаимодействии объективной случайности микромира со структурой пространства-времени, которая описывается специальной теорией относительности Эйнштейна. Это новая гипотеза автора статьи. Впервые удалось довести абстрактные теоретические представления по проблеме "стрелы времени" до экспериментально проверяемых фактов. Автором предсказано принципиально новое макроскопическое явление, которое, по-видимому, уже наблюдалось в экспериментах Российских ученых. Новые представления о природе необратимости помогут лучше понять окружающие нас повседневно процессы электрического сопротивления, трения, загрязнения, старения и, возможно, уменьшить связанные с ними потери и неудобства.

В основах современного естествознания есть противоречие, которое является ключевым. Оно более века зажигает эмоциональные дискуссии в среде физиков, математиков и философов. Оно тесно связано с глубокими проблемами в основах квантовой теории, статистической механики, теории алгоритмов и теории информации. Многочисленные попытки его разрешения породили целый ряд новых научных направлений. Это противоречие тесно связано с нашим мировоззрением и постоянно находится под пристальным вниманием идеологов. Оно разделяет мир на части - обратимый и необратимый, микроскопический и макроскопический, детерминированный и случайный.

В чем же заключается это противоречие? Это противоречие между необратимой во времени эволюцией макроскопических систем, то есть систем, состоящих из большого числа частиц и обратимостью фундаментальных физических законов движения.

ИСТОРИЧЕСКОЕ
ВВЕДЕНИЕ

Исторически сложилось так, что первыми были открыты фундаментальные законы классической механики - законы Ньютона, которые применялись к макроскопическим телам как к целому. Эти законы обратимы, то есть, не зависят от направления времени. Уравнения механики симметричны - не изменяются при замене t на - t . Механика Ньютона, дополненная в начале прошлого века аналитическими методами Лагранжа и Гамильтона, долгое время считалась идеалом физической теории. Она представляла собой замкнутую универсальную систему знаний, в принципе способную дать ответ на любой поставленный вопрос. Предсказать будущее и заглянуть в прошлое. Предсказания классической теории строго детерминированы, то есть в ней нет места случаю. Классическая механика прекрасно описывала (в пределах погрешностей измерений того времени) движение планет, которые дают хороший пример обратимой макроскопической механической системы. Если луну закрутить вокруг земли в противоположном направлении, то она будет вращаться точно так же, как она и вращается на самом деле.

Успехи классической механики, совпавшие по времени с эпохой Великой Французской революции, породили веру в то, что наука способна дать решения всех проблем и оказали огромное влияние на мировоззрение общества. Социалист утопист Сен-Симон даже предлагал учредить поклонение Ньютону в особых храмах, а общество должно было бы управляться "Великим Ньютонианским Советом", состоящим из знаменитых ученых.

Революционные изменения в физических представлениях, произошедшие в начале нашего века, почти не затронули обратимого характера фундаментальных физических законов. Релятивистская теория - специальная теория относительности Эйнштейна, устранившая противоречие между классической механикой и электродинамикой Максвелла, не зависит от направления времени и остается строго детерминированной теорией. Обратимыми во времени являются и уравнения квантовой механики. Однако квантовая теория уже содержит в себе принципиально неустранимую, объективную случайность и элементы необратимости, которые мы обсудим позже. Обратима и релятивистская квантовая теория - квантовая теория поля, объединяющая квантовую механику со специальной теорией относительности, которая лежит в основе физики элементарных частиц. Это значит, что любой физический процесс с элементарными частицами может быть осуществлен как в прямом, так и в обратном направлении (иногда с заменой частиц на античастицы и пространственной инверсией). Релятивистская квантовая теория позволила создать атомную и водородную бомбы, эти наиболее разрушительные достижения науки нашего века.

"Куб теорий"  В основании куба расположены "механические" теории. Они претендуют на максимально точное описание природы.  В верхней части куба расположены "статистические" теории. Они связывают микро и макро уровень описание явлений, не претендуя на полноту описания.  Отдельно расположена термодинамика. Она дает общие соотношения, не интересуясь внутренним строением вещества.  Решение проблемы видимо следует искать в одном из наиболее сложных разделов физики.

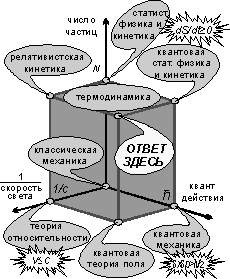
Перечисленные теории лежат в основе современных физических представлений и наглядно показаны на рисунке в основании "куба теорий". Они прекрасно описывают результаты эксперимента, если в нем участвует не слишком много частиц. Примечательно, что квантовая механика и специальная теория относительности привнесли в естествознание две фундаментальные константы. Это скорость света в вакууме с = 3 10⁸ м/с и квантовая постоянная, известная как постоянная Планка h = 6 10 ^-34 Дж с . С ними связанны два фундаментальных неравенства. Скорость любого физического сигнала v не может превышать скорость света v <= c . Наиболее известная форма другого неравенства - соотношения неопределенности Гейзенберга, связывает квантомеханическую неопределенность координаты и импульса частицы . В простейшем случае импульс это произведение массы частицы на ее скорость, однако, и безмассовая частица фотон обладает импульсом p = E/c, где E - энергия фотона. Несмотря на свое революционное влияние на мировоззрение, все новые теории не противоречат друг другу и классической механике. Они удовлетворяют Принципу Соответствия, который гласит, что новая теория должна переходить в уже известную теорию в области применимости последней. Уравнения специальной теории относительности и уравнения квантовой механики переходят в уравнения классической механики при предельных переходах 1/c стремится к 0 и h стремится к 0 по ребрам "куба теорий". Принцип Соответствия справедлив и для квантовой теории поля.

В середине прошлого века из практических потребностей создания тепловых машин параллельно с совершенствованием механики была развита поразительная по своей общности и кажущейся простоте наука термодинамика. Термодинамика не интересуется внутренним строением вещества и из общих соображений, основанных на данных опыта, отвечает на вопросы о том, что произойдет с макроскопическим телом, если его, например, сжать или расширить, нагреть или охладить. Термодинамика ввела в науку две важных величины - температуру T и энтропию S , которые не имеют никакого микроскопического или механического смысла, а могут характеризовать лишь равновесное состояние системы из большого числа частиц. Важнейшим результатом термодинамики явилось осознание того факта, что ряд процессов в природе принципиально необратим. Каждая замкнутая теплоизолированная система, например газ, будучи предоставлена самой себе, стремится к состоянию равновесия. Это обстоятельство нашло строгую формулировку в виде знаменитого второго начала термодинамики Клаузиуса, которое утверждает, что энтропия S замкнутой системы может только увеличиваться с течением времени dS/dt >= 0 . Необратимые процессы стремления систем к равновесию изучает физическая кинетика.

Позже было осознано, что необратимые процессы или процессы диссипации (рассеяния) окружают нас повсеместно и, как правило, связаны со всевозможными потерями и неудобствами. Это всем известное трение, из - за которого изнашиваются детали машин и нагреваются тормоза. Это и электрическое сопротивление, из-за которого на пути от электростанции до вашего утюга 15 - 20 процентов электроэнергии тратится на вредный нагрев проводов, что при плохой электропроводке приводит к пожарам. Это и загрязнение вашей одежды или окружающей среды за счет диффузии разнообразной грязи. Всем известно, что испачкаться легко, а отмыться или собрать разлитую нефть порой очень трудно. Это и перенос тепла от более горячего тела к холодному, из-за которого остывает ваш чай. И, наконец, мы стареем и умираем из-за необратимых процессов, протекающих в наших организмах. Не смотря на важность всех этих процессов, их микроскопическая природа до сих пор не ясна.

Учеными было создано большое количество разнообразных теорий, которые успешно описывают необратимые процессы. К ним относятся теория теплопроводности, газовая динамика, макроскопическая электродинамика и многие другие. Однако все эти теории являются более или менее феноменологическими, то есть основанными на постулатах, взятых непосредственно из опыта, и используют некоторые характеристики вещества, которые необходимо измерить. Большинство ученых считают эти теории практически полезными, но не фундаментальными.

Задача обоснования макроскопических законов термодинамики и физической кинетики на основе законов механики, применяемых на микроскопическом уровне, то есть к атомам и молекулам, стояла с середины прошлого века. Основополагающие результаты в этом направлении связаны с именами Больцмана и Гиббса. Эти ученые, основываясь на строго детерминированной классической механике (квантовой теории тогда еще не было) вынуждены были ввести в физику статистический или вероятностный подход. Естественной мотивировкой его введения было то, что макроскопические тела состоят из огромного числа атомов и молекул (порядка числа Авогадро 10²³ ) и нет никакой практической возможности, да и необходимости следить за движением каждого атома для полного механического описания движения системы. Следует изучать лишь средние микроскопические характеристики. Статистический подход оказался весьма плодотворным и позволил связать макроскопические свойства вещества со свойствами составляющих его атомов и молекул. Это дало возможность теоретически рассчитывать ряд макроскопических свойств веществ, таких как теплоемкость, вязкость, теплопроводность, которые до этого определялись лишь экспериментально. К сожалению, эти расчеты очень сложны и большинство свойств по-прежнему измеряется в эксперименте. Статистическому подходу отвечает вертикальное ребро на "кубе теорий", исходящее из классической механики.

Людвиг Больцман первый открыл микроскопический смысл термодинамической энтропии S как меры молекулярного хаоса и предложил кинетическое уравнение для молекул разреженного газа, из которого следовал закон возрастания энтропии. С тех пор в физической литературе необратимые процессы интерпретируются как процессы стремления молекул к беспорядку, хаотизации, потери информации, забывания начальных условий и т.п. Уравнение Больцмана необратимо во времени и первоначально вызвало ожесточенную критику как противоречащее основным принципам механики. Однако позже появился ряд строгих математических выводов уравнения Больцмана и ряда других необратимых кинетических уравнений непосредственно из уравнений классической механики. Тем не менее, все эти математические выводы содержат ту или иную дополнительную искусственную процедуру, например, осреднение по малому объему, обрыв зацепляющейся цепочки уравнений, сглаживание быстро осциллирующего интеграла или отбор части начальных условий, которые и позволяют нарушить временную симметрию уравнений механики. Таким образом, благодаря статистическому подходу противоречие между обратимыми уравнениями механики и вторым началом термодинамики переместилось с макроскопического на микроскопический уровень описания необратимых процессов, однако не было разрешено.

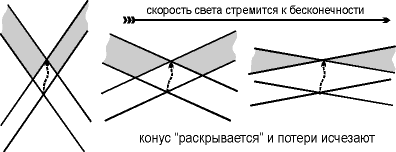
С открытием специальной теории относительности и квантовой механики статистическая механика и необратимые кинетические уравнения были обобщены на релятивистский и квантовый случаи. Парадоксально, но эти более сложные, чем классическая механика, теории позволили даже упростить решения целого ряда вопросов статистической физики и кинетики. Например, простым следствием квантовой статистики стало до этого постулируемое третье начало термодинамики, которое утверждает, что при абсолютном нуле температуры ( -273 ° C ) энтропия равна нулю. Релятивистский вывод уравнения Больцмана проще классического и для разреженного газа позволил установить, что макроскопическая и микроскопическая необратимости (то есть необратимость реакции между столкнувшимися элементарными частицами) не связаны между собой. С развитием математических методов квантовой теории поля оказалось, что некоторые из них применимы и в статистической физике. Эти обстоятельства позволяют заподозрить, что физические причины макроскопической необратимости следует искать в релятивисткой квантовой теории многих частиц. Однако релятивистская квантовая теория чрезвычайно сложна. Поэтому практически все усилия ученых до сих пор ограничивались анализом лишь классического и, реже, квантового случая. Считается, что релятивистские эффекты существенны, только если скорости частиц сопоставимы со скоростью света. Ими вполне обоснованно пренебрегали, поскольку скорости частиц газа - порядка скорости звука невелики при обычных температурах. Во многих системах пренебрежимо малы и квантовые эффекты.

Попытки отыскать естественный формализм, позволяющий устранить это противоречие и понять физическую природу необратимости, активно продолжаются и поныне. Более подробно с ними можно ознакомится по замечательным книгам нобелевского лауреата Ильи Пригожина "От существующего к возникающему", "Время, хаос, квант", который несколько последних десятилетий напряженной работы посвятил этой проблеме.

ГДЕ ИСКАТЬ
РЕШЕНИЕ

Гипотеза о том, что необратимость имеет квантовую природу, давно находится в поле зрения ученых. Дело в том, что, несмотря на обратимость своих уравнений, квантовая механика существенным образом содержит неэквивалентность обоих направлений времени. Эта неэквивалентность проявляется в связи с ключевым для квантовой теории процессом взаимодействия квантового объекта с измерительным прибором. Причем известно, что измерительный прибор должен быть макроскопическим и необратимым. В противном случае можно придумать квантовый вечный двигатель, нарушающий второе начало термодинамики. В таинственном процессе взаимодействия квантового объекта с классическим прибором необратимо реализуется один из возможных исходов эксперимента с квантовым объектом, вероятность которого и позволяют рассчитать обратимые и детерминированные уравнения квантовой механики. Причем граница между квантовым объектом и классическим прибором четко не определена. Такое положение дел не устраивало многих ученых, с самого момента создания квантовой теории. Однако многолетние попытки придумать что-то существенно лучшее пока не увенчались успехом. Тем более что самые удивительные предсказания квантовой теории неизменно находят экспериментальное подтверждение.

Сильным аргументом в пользу наличия тесной связи между квантовыми эффектами и необратимостью являются два наблюдаемых в эксперименте макроскопических квантовых явления - сверхтекучесть и сверхпроводимость. Они как раз и заключаются в том, что при низких температурах, достаточных для проявления квантовых эффектов, в жидком гелии пропадает вязкость, а в целом ряде веществ электрическое сопротивление. Это значит, что макроскопическое течение сверхтекучей части жидкости, и протекание электрического тока становится обратимыми. Сверхтекучий гелий ведет себя весьма удивительным образом. Например, если его налить в стоящую на блюдце чашку, то вопреки силе тяжести он будет "выползать" из чашки на блюдце (а затем и на стол) до тех пор, пока уровень жидкости в них не выровняется.

Ландау и Лившиц в их всемирно известном курсе теоретической физики писали, что "в принципе закон возрастания энтропии мог бы быть макроскопическим выражением физической неэквивалентности направлений времени в квантовой механике. В таком случае должно было бы существовать содержащее квантовую постоянную h неравенство, обеспечивающее справедливость этого закона и выполняющееся в реальном мире". Однако до сих пор такое неравенство предложено не было.

Строгое общепринятое определение необратимого процесса, применимое в общем случае, в настоящее время отсутствует. Мы лишь можем с уверенностью утверждать, что та или иная математическая модель реальности является обратимой или необратимой. Однако ясно, что обратимый процесс в природе является скорее идеализацией, чем реальностью. Каждый реальный процесс хотя бы чуть-чуть необратим. Даже луна, вызывая приливы воды в океане и магмы в земном ядре, а значит, вязкое трение воды о берега и магмы внутри земли, медленно расходует свою энергию и увеличивает период своего вращения вокруг земли, а также продолжительность земных суток. По данным астрономов всего на 0.0181 секунду за тысячу лет. При этом, однако, диссипирует 3 10¹² ватт, то есть мощность пятисот Красноярских ГЭС, что, конечно же, мелочь в планетарном масштабе.

Универсальный характер необратимости заставляет предположить, что существует единый физический механизм, приводящий к выделению направления времени. Причем он должен быть предельно простым, поскольку сложное не может быть общим.

УГАДАЕМ
РЕЗУЛЬТАТ

Основной результат данной статьи легко "угадать" из соображений размерности. Найдем ответ на следующий простой вопрос. Какие еще фундаментальные физические константы может содержать неравенство, о котором писали Ландау и Лившиц? Ограничимся простейшим случаем однородной и изотропной среды без химических реакций. Действительно, в общем случае могут возникнуть лишь дополнительные константы, но уже включенные константы исчезнуть не могут. С другой стороны, общий физический механизм, приводящий к необратимости должен работать и в простейшем случае. Рассмотрим большую систему, например газ, первоначально выведенную из состояния термодинамического равновесия. Условиями равновесия являются однородность температуры и давления, знание которых полностью определяет термодинамическое состояние системы. Изучим поведение системы на больших временах. Поскольку, как правило, давление достигает равновесия быстрее температуры, предположим, что давление уже выровнялось, и исследуем процесс роста энтропии изза окончательного выравнивания температуры. Искомое неравенство должно усиливать второе начало термодинамики dS/dt >= ? >= 0 . Поскольку энтропия системы является суммой энтропий ее частей, в неравенстве должен стоять интеграл по объему системы. Используя соображения симметрии (формула не должна меняться при сдвигах и поворотах системы отсчета) и общие термодинамические соотношения нетрудно показать, что этот интеграл должен иметь вид

Среди ученых имеется много различных точек зрения о том, из каких соображений и какие физические постоянные следует считать фундаментальными. Здесь же естественно считать, что постоянная Больцмана k=1.38 10^-23 Дж/К не является фундаментальной. Она лишь устанавливает связь между единицей энергии джоулем и единицей температуры градусом. Мы могли бы проградуировать все термометры в джоулях и обойтись без нее вовсе. Это просто неудобно. Если исключить постоянную Больцмана, то энтропия будет безразмерной, а температура будет иметь размерность энергии. Чтобы сократились джоули, следует поделить правую часть на квантовую постоянную h в квадрате. (Постоянная h имеет размерность джоуль*секунда). Нетрудно подсчитать, что для того чтобы согласовать размерности правой и левой части, теперь не хватает константы размерности скорости. В итоге получим a ~ 1/h²c . Чтобы вернуться к обычной системе единиц СИ, следует умножить a на куб постоянной Больцмана k . Окончательно получим

Возможно ли присутствие каких - нибудь еще фундаментальных постоянных, быть может, безразмерных, в полученном неравенстве? Анализ показывает, что невозможно. Только эти две константы фигурируют в фундаментальных механических неравенствах - ограничении максимальной скорости распространения взаимодействий Эйнштейна и соотношения неопределенности Гейзенберга. Другие константы используются лишь в равенствах. Таким образом, полученное неравенство видимо и является предельным случаем неравенства, существование которого предполагали Ландау и Лившиц. Оно справедливо лишь в случае малого отклонения системы от состояния равновесия. Видимо никакого другого, более общего неравенства для энтропии в настоящее время и не может быть предложено. Это связано с тем, что общего определения энтропии для произвольной неравновесной системы пока просто не известно, несмотря на многочисленные попытки ее определить, хотя необратимость эволюции во времени имеет интуитивно понятный смысл в любом случае.

К сожалению, непосредственная экспериментальная проверка неравенства для энтропии невозможна, поскольку в арсенале физических приборов отсутствуют "энтропомеры". Энтропия всегда вычисляется на основе измерения других физических величин. Сравним полученное неравенство с известной формулой для скорости увеличения энтропии за счет теплопереноса

В простейшем случае пластины толщины l , поверхности которой находятся при температурах T₁ и T₂ , поток энергии через квадратный метр пластины равен

Коэффициент пропорциональности A (Вт/м К) называется коэффициентом теплопроводности и чаще измеряется экспериментально. Легко видеть, что неравенство для скорости роста энтропии может быть интерпретировано как существование фундаментальной нижней границы коэффициента теплопроводности

Полученное неравенство усиливает второе начало термодинамики и справедливо в пределе малого отклонения системы от равновесия. Помимо постоянной Планка h оно содержит и скорость света. Это значит, что необратимость является не только квантовым, но и релятивистским эффектом. Второе начало термодинамики постулирует, основываясь на опыте, что тепло передается только от горячего тела к холодному. Новое неравенство утверждает, что существует минимально возможная скорость переноса тепла от горячего тела к холодному. Тепловой поток это количество энергии, которое передается за одну секунду через квадратный метр пластины. Он пропорционален перепаду температур и обратно пропорционален толщине пластины. Фактически мы вывели ограничение на коэффициент этой пропорциональности - коэффициент теплопроводности, который и является мерой скорости переноса тепла.

СРАВНИМ С
ЭКСПЕРИМЕНТОМ

Неравенство для теплопроводности уже можно сравнить с экспериментальными данными. Например, при комнатной температуре A_min(300K)~1.73 10^-5 Вт/м К. Это значение лишь приблизительно в сто раз меньше коэффициента теплопроводности в вакууме лучших теплоизоляторов ( ~2 10^-3 Вт/м К ), которые состоят из тончайших, несколько молекул в диаметре, волокон кварца и специального порошка зачернителя. Для сравнения, теплопроводность обычных теплоизоляционных материалов вроде стекловаты или пенопласта примерно в двадцать раз больше. Следовательно, теоретическая граница недалека от реальности и вполне доступна современной экспериментальной технике. Минимальная теплопроводность увеличивается пропорционально квадрату температуры. Просмотрев много толстых справочников, содержащих экспериментальные данные, можно убедится, что полученное неравенство для теплопроводности не нарушается ни при высоких, ни при низких температурах.

Ограничение на минимальное значение теплопроводности, казалось бы, должно нарушаться в вакууме. Однако в вакууме между двумя непрозрачными поверхностями с температурами T₁ и T₂ имеется тепловое электромагнитное излучение, которое переносит энергию от горячей поверхности к холодной точно так же, как солнце греет землю (видимый свет это тоже тепловое излучение солнца) или электрокамин с рефлектором греет ваши ноги. В обычном термосе, для того, чтобы медленнее остывал чай, стенки вакуумной стеклянной колбы изнутри покрывают зеркальным слоем металла, который почти все отражает, а значит и слабо испускает тепловое излучение. Теплообмен в зазоре между двумя хорошо проводящими, а значит мало излучающими, металлами дает интересный и важный способ экспериментальной проверки фундаментального неравенства для теплопроводности. Из формулы для теплового потока q = A(T₂-T₁)/l , а значит, q >= A_min(T₂-T₁)/l очевидно, что поток тепла должен возрастать при уменьшении зазора обратно пропорционально его ширине l . Но в элементарной теории поток теплового излучения не зависит от ширины зазора.

Обратимся к эксперименту, проведенному около двадцати лет назад в Институте теплофизики Сибирского отделения Академии наук. Там измеряли зависимость теплового потока от ширины зазора между двумя полированными медными дисками в вакууме. На графике сопоставлены наша оценка и экспериментальные данные при температуре одного диска 77 , а другого 150 градусов Кельвина (- 196 и - 123 ° С). Видно, что при ближении дисков тепловой поток начинает расти в полном соответствии с нашими предсказаниями. На том же графике приведены результаты расчета потока по теории теплообмена флуктуационным электромагнитным полем. Эта теория тоже предсказывает рост теплового потока обратно пропорционально ширине зазора, но его рост начинается при ширине зазора примерно в десять раз меньшей, чем наблюдается в этом эксперименте. Теория теплообмена флуктуационным электромагнитным полем представляет собой синтез макроскопической электродинамики и статистической физики. Она развивалась, начиная с пятидесятых годов, с целью расчета тепловых шумов антенн, резонаторов, волноводов и других радиотехнических устройств. Однако, насколько известно автору, практического применения эта теория не получила. Расчеты показывают, что ее расхождение с нашей оценкой в предсказании расстояния, начиная с которого должен наблюдаться рост теплового потока, не зависит от температуры и может достигать ста и более раз. Таким образом, в эксперименте можно получить однозначный ответ, какая из теорий справедлива.

Поток тепла между медными дисками в вакууме  Здесь сопоставлены результаты эксперимента и расчет по нашей оценке.  Приведен расчет и по теори электро - магнитных флуктуаций.

Насколько известно автору, в настоящее время не существует последовательной теории, которая позволила бы рассчитать теплообмен в вакуумном зазоре между двумя хорошими проводниками. Мы получили лишь теоретическую оценку его минимально возможного значения. Известны несколько грубых инженерных моделей, которые, однако, вполне достаточны для практических нужд расчета вакуумной экранной теплоизоляции. По-видимому, двадцать лет назад ученые Института теплофизики наблюдали новый макроскопический релятивистский квантовый эффект, и, не подозревая, что собственно они наблюдают. Похожие эксперименты с качественно близкими результатами проводились около тридцати лет назад в Соединенных штатах и Голландии. Однако поскольку цели у всех трех экспериментальных групп были сугубо прикладными, их необычные результаты остались незамеченными в бурном потоке научных публикаций.

Макроскопических квантовых явлений известно не так уж много. Это уже упоминавшиеся эффекты сверхтекучести и сверхпроводимости, а также ряд других, в основе которых лежит сверхпроводимость. Открытие этих эффектов и разработка весьма сложных теорий, которые их объясняют, отмечены несколькими нобелевскими премиями. Примечательно, что все они наблюдаются только при низких температурах. Открытая в 1986 году высокотемпературная сверхпроводимость исчезает при 125 К (- 148 ° С) и несмотря на многолетние усилия многих ученых, окрыленных надеждой создать сверхпроводник, работоспособный при комнатных температурах, до сих пор не нашла удовлетворительного теоретического объяснения.

Единственным известным макроскопическим релятивистским квантовым эффектом является эффект Казимира, который заключается в возникновении слабой силы притяжения между металлическими пластинами, которая обратно пропорциональна четвертой степени расстояния между ними. Так считает профессор Хокинг, заведующей кафедрой в Кембридже, той самой, которой в свое время руководил Ньютон. Хокинг знаменит тем, что теоретически предсказал, будто даже черные дыры не совсем черные, а испускают очень слабое тепловое излучение, которого, впрочем, никто не видел, как и сами черные дыры. Однако не все специалисты разделяют его точку зрения на эффект Казимира. Силу Казимира можно объяснить и теорией электромагнитных флуктуаций, которая приводит к той же теоретической зависимости, а, следовательно, выбор между конкурирующими теориями не может быть сделан на основе эксперимента.

Рост теплового потока при уменьшении зазора между металлами наблюдается при любых температурах. Его наблюдаемая величина существенно отличается от предсказаний всех известных теорий. Тепловой поток измерить гораздо легче, чем силу Казимира. Поэтому эффект роста теплового потока представляется чрезвычайно важным новым макроскопическим релятивистским квантовым эффектом. Он нужен для проверки новых теорий, призванных решить проблему необратимости. Например, очень интересных результатов можно ожидать, если использовать сверхпроводящие диски вместо медных.

Важно то, что теперь проблема необратимости, бывшая до сих пор, в лучшем случае, объектом усилий чистой теории, а чаще метафизики и философии, наконец, встает на твердую экспериментальную почву.

СЛЕДСТВИЯ
ДЛЯ ТЕОРИИ

Мы убедились, что "угаданный" результат, по крайней мере, нелегко опровергнуть экспериментально. Он представляет собой нечто новое, поскольку значительно расходится в своих предсказаниях с существующей теорией. Обсудим его следствия, концептуально важные для дальнейшего развития теории.

Прежде всего, отметим, что наличие фундаментальной нижней границы для коэффициента теплопроводности означает, что замкнутых систем в природе принципиально не существует. Можно показать, что это макроскопическое следствие объективной нелокальности релятивистской квантовой теории, которая на микроскопическом уровне проявляется в таких активно изучаемых в последнее время эффектах как, например, "квантовая телепортация" и в целом ряде других. В этих экспериментах фотон "чувствует" состояние другого фотона, который может находится за несколько километров от него.

Для термодинамики отсутствие замкнутых систем такая же "неприятность", как для классической механики - квантовое соотношение неопределенностей Гейзенберга. Специалисты по термодинамике, конечно, прекрасно понимают, что абсолютно теплоизолированная система практически неосуществима. Это только удобная физическая идеализация. Однако считалось, что специальными ухищрениями к ней можно приблизится с любой степенью точности. Теперь ясно, что она неосуществима в принципе. Точно также в начале века специалисты по классической механике прекрасно понимали, что практически невозможно измерить координату и импульс частицы, точное знание которых позволило бы предсказать все ее будущее и восстановить ее прошлое. Однако считалось, что принципиальных ограничений не существует и все дело в совершенствовании технических возможностей. Квантовая теория разрушила идиллию детерминизма, установив, что это невозможно в принципе. Достаточно малую частицу невозможно полностью "зажать" в тисках измерительного прибора, она обязательно "вывернется", оставив за собой некоторую свободу выбора.

Другим важным следствием полученных неравенств является понимание того, что необратимость является не только квантовым, но и принципиально релятивистским явлением. На это указывает присутствие в неравенствах скорости света. На первый взгляд, этот вывод кажется парадоксальным. И крайне пессимистичным в плане перспектив создания микроскопической теории необратимых процессов. В ее основе теперь должны лежать результаты крайне сложной квантовой теории поля. А что толку в слишком сложной теории, выводы которой трудно довести до практических рекомендаций? Однако ситуация далеко не так безнадежна. Ее я постараюсь описать в следующих статьях, разъясняющих микроскопический вывод "угаданных" неравенств.

Здесь мы разберем, каким образом могут проявляться релятивистские квантовые эффекты, крайне малые, например, в благородном газе аргоне при нормальных условиях, который хорошо описывается классической теорией. Ответ на данный вопрос дает сравнительно недавно развитая теория детерминированного хаоса. Эта математическая теория изучает класс систем, в которых нет места случаю, но которые, тем не менее, внешне ведут себя как случайные. Траектории частиц в таких системах неустойчивы к малым возмущениям, поскольку, будучи первоначально близки, они очень быстро удаляются друг от друга. Это приводит к быстрому запутыванию траекторий и перемешиванию частиц. Неустойчивость многократно усиливает возмущения классического движения, причиной которых являются малые релятивистские квантовые эффекты. Это обстоятельство и разрешает кажущийся парадокс между малостью релятивистских квантовых эффектов и наблюдаемым процессом установления термодинамического равновесия в почти классическом газе.

ПРИРОДА НИЧЕГО
НЕ ЗАБЫВАЕТ

Теперь мы можем попытаться понять наш основной результат - ключевую роль структуры пространства - времени для необратимых процессов. Для этого, вспомнив основы специальной теории относительности, рассмотрим одну классическую частицу. К счастью, теория относительности содержит одно абсолютное понятие. Это световой конус в четырехмерном пространстве - времени (t,x,y,z) . Для наглядности на следующем рисунке три пространственные координаты (x,y,z) обозначены как одна ось x, а конус "выродился" в крестик. Световой конус абсолютен, поскольку скорость света не зависит от выбора системы отсчета. Он разбивает все события в пространстве - времени на три части - абсолютно прошедшие, абсолютно будущие и абсолютно удаленные события. Только события, лежащие в конусе прошлого (нижняя часть), могут влиять на частицу в пункте А . Частице доступны события, лежащие в конусе будущего. Абсолютно удаленные события недоступны для частицы, и частица в пункте А недоступна для них.

Световой конус  Он разбивает все события в пространстве - времени на три части - прошедшие, будущие и удаленные.  Световой конус абсолютен потому что не зависит от выбора системы отсчета.

Рассмотрим движение одной классической частицы. Двигаясь вдоль траектории AB из пункта A в пункт B , частица увлекает с собой свой световой конус, который переходит в новый световой конус (серый). Траектория частицы может лежать только внутри конуса будущего, поскольку скорость частицы ограничена скоростью света.

Эволюция светового конуса во времени  С течением времени классическая частица, перемещаясь в пространстве, увлекает с собой свой световой конус.   В результате этого часть событий, доступных ранее, становятся принципиально недоступны для частицы.   Это и является причиной необратимых процессов в природе и технике.

Легко видеть, что необратимость может быть интерпретирована как потеря части будущего, доступного частице (закрашено темным). Для любой траектории при произвольном выборе системы отсчета эти потери неизбежны.

Отметим, что ограниченность скорости необходима, поскольку при формальном стремлении скорости света к бесконечности световой конус "раскрывается" и потери доступного будущего исчезают. Становится понятным, почему многолетние усилия теоретиков не привели к решению проблемы необратимости. Если мы возьмем за основу нерелятивистский вариант механики, значит, мы уже перешли к пределу с = 0 , а, следовательно, уже выплеснули ребенка.

Нерелятивистский предел  Мы принципиально не можем построить теорию необратимых процессов опираясь на вариант механики, который не учитывает конечности скорости распространения физических сигналов.

Новая интерпретация необратимости противоречит широко распространенной точке зрения на необратимые процессы как на процессы "забывания" начальных условий, хаотизации, ослабления корреляций, потери информации и т. п., которые являются процессами "утраты прошлого". Природа ничего не забывает! Старый конус прошлого лежит внутри нового конуса прошлого.

Новая интерпретация необратимости интуитивно очевидна, поскольку наше тело является классическим. Если вы читаете эту статью, вы необратимо теряете возможность поиграть в футбол. Но никто не может отнять у вас вашего прошлого. Таким образом, необратимость естественно трактовать как утрату части доступных альтернатив.

Особенно важно отметить, что наш рисунок обратим. Если мы изменим направление времени на противоположное (перевернем рисунок), что поменяет прошлое и будущее, то частица будет двигаться из пункта B в пункт A и по прежнему будет терять часть будущего. В этой связи вспоминается точка зрения Эйнштейна, который считал, что необратимые процессы не более чем иллюзия.

Обращение времени  При смене знака времени на противоположный прошлое симметрично меняется с будущем, но потери остаются. Это обстоятельсво разрешает известное противоречие между обратимосью механических теорий и необратимостью макроскопических процессов.

В квантовом случае ситуация не столь очевидна, поскольку понятие траектории кантовой частицы теряет смысл. Для квантовой частицы с определенной координатой доступен весь световой конус, поскольку ее скорость неизвестна в соответствии с соотношением неопределенности. При использовании стандартной интерпретации квантовой механики, будущее теряется лишь в момент необратимого измерения наблюдателем координаты частицы в пункте B . Однако в квантовой теории отсутствует четкая грань между квантовым объектом и измерительным прибором, а процесс измерения объективен. Поэтому нам ничто не мешает объявить нашу частицу (или любую их совокупность) квантовым объектом, а всю остальную систему - измерительным прибором. Тогда получится, что необратимые процессы в природе результат ее "самоизмерения".

Воспользовавшись словами Эйнштейна, можно сказать, что квантовая частица, взаимодействуя с окружением, по "собственному свободному решению выбирает" одну из альтернатив. Однако она выбирает ее в рамках закона, то есть так, чтобы соблюсти поддающиеся расчетам вероятности альтернатив. Точно также мы ходим туда, куда сами того хотим, подчиняясь при этом не знающему исключений закону всемирного тяготения.

Разумеется, столь крайняя точка зрения сегодня не может трактоваться буквально. Однако ее труднее принять, чем понять. Известна философская концепция, что принципиально вероятностный характер предсказаний в квантовой механике является физической основой свободы воли. Эта идея не противоречит детерминизму. Кстати становится понятным, отчего явления самоорганизации, которые изучаются последователями Ильи Пригожина в качестве возможного моста между живой и неживой природой, наблюдаются только в диссипативных системах.

ЧТО
ДЕЛАТЬ

Оставим философские проблемы философам. Приведенные аргументы позволяют предположить, что противоречие между обратимой релятивистской квантовой теорией и наблюдаемой необратимостью макроскопических систем исчезнет, если нам удастся непротиворечивым образом включить процесс "измерения" в теорию. Над нерелятивистской квантовой теорией измерений ученые бьются с момента создания квантовой механики, однако, вопрос до сих пор остается открытым. Теперь есть надежда, что ответ будет найден в релятивистской теории.

По-видимому, обратимые уравнения механики и необратимые кинетические уравнения по сути дела две упрощенные модели реальности, которые отражают различные грани природы. Не следует пытаться выводить кинетические уравнения из уравнений механики, а следует пытаться построить объединяющую теорию, из которой предельными переходами по количеству частиц в системе будет получаться и механика, и кинетика.

Все практические приложения данной работы сегодня трудно предвидеть. Очевидно, что благодаря развитию теории можно будет создать более совершенные теплоизоляционные материалы, уменьшить шумы в устройствах радиоэлектроники, возможно, лучше понять явление сверхпроводимости.

Это долгосрочная программа. Предстоит еще много работы, прежде чем описанные результаты, не смотря на их кажущуюся очевидность, будут приняты научным сообществом. В науке как в хорошем детективе. От уверенности следователя в личности преступника до сбора всех необходимых доказательств, которые убедят присяжных заседателей, большой объем работы. Необходимо проанализировать все теоретические следствия для различных разделов физики. Многие из них не поместились в статью. Необходимо иначе поставить и тщательно повести эксперименты.

К сожалению, эксперименты по теплообмену в зазоре, не смотря на всю простоту своей постановки, весьма трудоемки, поскольку требуют создания высокого вакуума, точного измерения малых расстояний и малых тепловых потоков.

При сегодняшнем уровне финансирования фундаментальной науки даже дальнейшее развитие теории, не говоря уж о проведении экспериментов, упирается в отсутствие средств.