Гл. 3. Проблема равномерности времени
Начиная с Аристотеля, во все последующие времена одним из наиболее важных и фундаментальных свойств времени считалась и по сей день считается равномерность. Однако вплоть до возникновения классической механики не было сколь-либо серьезных попыток обосновать подобное представление. Даже в те далекие времена, когда еще не было механических часов, позволяющих практически измерять интервалы равномерного времени и неограниченно долго вести счет равных друг другу единиц измерения времени, и когда в повседневной практике вынуждены были пользоваться постоянно изменяющимися в течение года и в общем случае не равными друг другу "дневными" и "ночными" часами, мыслители проявляли удивительную уверенность в том, что истинное время на самом деле течет равномерно.
Аристотель рассматривал равномерность в качестве важнейшего, наряду с общедоступностью и максимальной простотой, критерия при поисках движения, наиболее пригодного для измерения времени. Таким движением Аристотель считает суточное вращение небесной сферы, или "сферы неподвижных звезд".
С его точки зрения, равномерность - настолько общеизвестное и самоочевидное свойство времени, что указание на него является веским аргументом при доказательстве истинности тезиса: "время не есть движение". “Изменение и движение каждого [тела], - пишет Философ, - происходит только в нем самом или там, где случится быть самому движущемуся и изменяющемуся; время же равномерно везде и при всем. Далее, изменение может идти быстрее и медленнее, время же не может, так как медленное и быстрое определяется временем: быстрое есть далеко продвигающееся в течение малого времени, медленное же - мало [продвигающееся] в течение большого [времени]; время же не определяется временем ни в отношении количества, ни качества” /Физ,IV,10,218b10-15/.
Согласно данному утверждению, для определения большего и меньшего движения мы должны иметь возможность сравнивать, какое расстояние проходят движущиеся тела за равные или заведомо большие или меньшие по сравнению с данным отрезком времени интервалы, т.е. здесь предполагается, что мы априори умеем оценивать и сравнивать между собой различные интервалы времени. Это возможно только в том случае, если мы допускаем, что время всегда течет одинаково, т.е. равномерно, и что наши единицы измерения времени (например, полные сутки) каждый раз одинаковы по длительности.
Единственное, на чем основывается представление о равномерности времени, - это интуитивная уверенность Аристотеля в том, что время - это нечто априори равномерное. И это не случайно. Дело в том, что, во-первых, невозможно непосредственно сравнивать между собой, как бы накладывая друг на друга, длительности таких естественных единиц измерения времени, как, например, длительности полных суток; во-вторых, во времена Аристотеля не существовало таких измерителей времени, как механические часы, которые достаточно долго сохраняли бы постоянство своего хода и таким образом давали бы возможность измерять и сравнивать между собой длительности отстоящих друг от друга интервалов времени.
Но проблема равномерности времени, как мы увидим позднее, не снимается даже после появления механических часов, поскольку для определения постоянства или непостоянства их хода необходимо или непосредственно сравнивать между собой следующие друг за другом отмериваемые ими единицы времени, что в принципе невозможно; или иметь некоторый заведомо равномерный стандарт измерения времени, но тогда проблема равномерности в полной мере переносится на этот стандарт; или, наконец, придумать какие-то особые критерии равномерности. Поэтому было бы тщетно искать у Аристотеля какое-либо обоснование равномерности времени, и, что бы ни думал сам Философ, единственным основанием представления о равномерности как о фундаментальном свойстве времени остается его (Аристотеля) интуитивная уверенность в том, что "время... равномерно везде и при всем".
Не преуспели в обосновании равномерности времени и более поздние мыслители. Например, ни у Плотина, ни у Аврелия Августина мы не найдем каких-либо попыток разъяснить это свойство времени. Согласно Плотину, равномерность является естественным и самоочевидным свойством тех движений, при помощи которых мы измеряем время /Эннеады, III, 7,9; III, 7, 12/. Что касается самого времени, то оно представляет собой равномерно развертывающуюся “в бесшумно наступающих изменениях” длину жизни души /III, 7, 12/. Точно так же и Аврелий Августин помещает время в душе и тем самым снимает проблему равномерности объективного времени.
Астрономы и философы-номиналисты позднего средневековья, как мы видели, продолжают рассматривать равномерность как одно из основных и самоочевидных свойств истинного времени. При определении движения, пригодного для измерения времени "в наиболее собственном смысле", средневековые последователи Аристотеля ради равномерности даже жертвуют таким его требованием к "мировым часам", как общедоступность для наблюдения ("наибольшая известность"), и признают в качестве такого движения вращение невидимой гипотетической "девятой" сферы. В результате происходит отделение равномерного времени от всех чувственно воспринимаемых движений и таким образом формируется идея абстрактного "математического времени", которое, в отличие от "времен", измеряемых при помощи чувственно воспринимаемых движений, протекает равномерно.
Однако средневековые перипатетики, хотя и оказались вынужденными обсуждать вопрос о множественности времен, тем не менее так же, как и Аристотель, не раскрыли природу равномерности "времени в наиболее собственном смысле" (т.е. времени "первого движения") и не смогли обосновать правомерность использования равномерного времени, отсчитываемого при помощи невидимой "девятой сферы", для измерения неравномерных земных движений. Как пишет В.П. Зубов, “позднейшее объяснение арабских мыслителей (Аверроэса), вводившее новое произвольное допущение космологического порядка, а именно указание на причинную обусловленность всех "подлунных движений" движением "мировой сферы", также не было ответом на поставленный вопрос. Единственное, что, быть может, заслуживает внимания, это более четкое различение двух видов мер: время обращения мировой сферы есть "внутренняя" мера движения этой самой сферы, для всех же других движений время ее обращения есть "внешняя", или непосредственно не связанная, с ними мера (mensura separata)” /Зубов, 1960, с.35/. Нерешенным, по мнению Зубова, остался также вопрос о том, что гарантирует равномерность вращения небесной сферы.
Природа и критерии равномерности времени оставались невыясненными и во времена И. Ньютона.
Так, Джон Локк (1632-1704) считал, что понятия последовательности и продолжительности мы получаем не из наблюдений внешнего движения, а из рефлексии последовательной цепи идей, появляющихся друг за другом в нашем уме /Локк, т. 1, 1985, с.232/. Согласно Локку, цепь идей в уме человека имеет известную степень быстроты. Этот тезис обосновывается тем, что человек не воспринимает как слишком быстрые, так и слишком медленные движения. В первом случае, события, слишком быстро следующие друг за другом, занимают время одной идеи и не могут быть различимы людьми. В случае же слишком медленных движений, “...другие идеи наших собственных мыслей имеют... возможность проникать в наш ум между идеями, которые доставляет нашим чувствам движущееся тело...", и "чувство движения исчезает”/Там же, с. 235/ (Здесь и далее курсив автора. - И.Х.)..
Следующим после приобретения идеи продолжительности естественным делом ума является “приобретение некоторой меры для этой общей продолжительности, по которой он мог бы судить о ее различной величине и рассматривать определенный порядок, в котором существуют вещи... Такое рассмотрение продолжительности как ограниченной известными периодами и обозначенной определенными мерами, или эпохами... и есть то, что мы называем собственно временем” /Там же, с.237-238/.
Итак, согласно Локку, время есть измеренная продолжительность. Причем хорошее измерение должно делить всю его продолжительность на равные периоды. Вместе с тем философ прекрасно понимает, что “мерой продолжительности может быть только продолжительность...” /Там же, с. 238/ и поэтому невозможно иметь “...какую-нибудь установленную неизменяемую меру продолжительности, состоящей в постоянной текучей последовательности, подобно тому, как мы имеем меры для измерения протяженных величин - дюймы, футы, ярды и т.д., раз отмеченные на прочном материале” /Там же/. Поэтому для измерения времени “может быть пригодно только то, что разделило всю величину его продолжительности на очевидно равные части постоянно повторяющимися периодами” /Там же/.
Такой наиболее подходящей мерой времени, считает Локк, являются вращения Солнца и Луны. Но в результате постоянного измерения времени при помощи этих движений люди стали думать, “будто движение и продолжительность измеряются одно другим, ибо при измерении величины времени люди привыкли к идеям минут, часов, дней, месяцев, лет и т.д. и о них начали думать всякий раз при упоминании о времени или продолжительности (а все эти отрезки времени измерялись движением небесных тел). Поэтому они стали склонны смешивать время и движение или по крайней мере думать, что они необходимо связаны друг с другом” /с.238/. На самом же деле, по Дж. Локку, время измеряется не самим движением Солнца, а его периодичностью, и поэтому для измерения времени не обязательно иметь какие-либо движения, а необходимо и достаточно иметь периодические процессы. “И если бы замерзание воды или цветение растения повторялись во всех частях света через равноотстоящие периоды, то они служили бы людям для счета лет так же хорошо, как и движение Солнца” /с.239/. Поэтому “мы... должны тщательно различать саму продолжительность от мер, которыми мы пользуемся для суждения о ее величине. Продолжительность сама по себе должна рассматриваться как движущаяся вперед одним постоянным, ровным и однообразным потоком. Но насколько нам дано знать, такою не способна быть ни одна из тех ее мер, которыми мы пользуемся; не можем мы быть уверены и в том, что их определенные части, или периоды, равны между собой по продолжительности, ибо, как бы мы ни измеряли две последовательные величины продолжительности, никогда нельзя доказать их равенства” /Там же, с. 240/.
В отличие от используемых в качестве меры времени периодических процессов, равенство периодов которых всегда остается под сомнением, понятие самой продолжительности, считает Локк, остается тем не менее ясным. Поскольку нет возможности непосредственно сопоставить длительности двух частей последовательности и поэтому нельзя знать с достоверностью их равенства, то для измерения времени остается только принять за меру времени непрерывные последовательные явления, следующие через периоды, кажущиеся равноотстоящими. Для определения этого равноотстояния “у нас нет другой меры, кроме той, которую для нашего убеждения в их равенстве в согласии с другими вероятными доводами запечатлела в нашей памяти цепь наших собственных идей” /с.241/. Иными словами, реально существует неограниченно длящаяся как в прошлое, так и в будущее равномерная продолжительность, ясную идею которой человек получает путем рефлексии равномерного потока идей в своем уме. Время же есть ограниченная часть этой продолжительности, измеренная той или иной относительно точной мерой - часом, сутками, годом и т.д.
Таким образом, согласно Локку, представление человека о равномерной длительности возникает в результате существования у него некоторой "постоянной и правильной последовательности идей", т.е. некоторого внутреннего движения идей или, выражаясь современным языком, "потока сознания". Однако кроме общих заверений, что это так и только так, Дж. Локк не может привести каких-либо разъяснений, почему "цепь наших собственных идей" всегда следует с одной и той же неизменной скоростью.
На протяжении всей доньютоновской истории философии и естествознания единственным основанием представления о равномерности времени (или длительности) оставалось субъективное чувство времени, или интуиция равномерного дления.
Не внес в этот вопрос ясности и Ньютон, который, фактически, постулировал существование, абсолютную равномерность и независимость ни от каких материальных объектов и процессов "абсолютного, истинного математического времени". При этом Ньютон отмечал, что, возможно, и не существует такого идеально равномерного процесса, при помощи которого можно было бы измерять абсолютное время, но он полагал, что достаточно хорошим приближением к абсолютному времени является исправленное при помощи "уравнения времени" относительное время, которое измеряется при помощи вращения Земли вокруг оси.
Активное стремление обосновать ньютоновскую концепцию времени мы находим у Ж.-Л. д'Аламбера.
Ж.-Л. д’Аламбер считал, что все доступные познанию свойства движения, пространства, времени и материи постигаются математикой или такими науками, как механика и физика, которые опираются в своей методологии на математику. Вопросы же о сущности познаваемых объектов д’Аламбер отвергает как "метафизические". Этими вопросами, считает он, могут заниматься лишь философские сектанты, которые, несмотря на все различия их сект, при познании, например, пространства, вынуждены пользоваться одной и той же геометрией.
Вполне понятно, что, стоя на подобных позициях, д’Аламбер не мог без критического анализа и определенной конкретизации признать в качестве объекта познания такую априорно постулируемую И. Ньютоном сущность, как "абсолютное, истинное математическое время". Принимая и отстаивая ньютоновскую концепцию времени, д’Аламбер не может, конечно, сделать абсолютное время доступным непосредственному восприятию и познанию. Более того, он согласен с Ньютоном в том, что, возможно, и не существует такое абсолютно равномерное движение, при помощи которого можно было бы измерять абсолютное время. Тем не менее он стремится доказать, что равномерность абсолютного времени - это его объективное свойство, которое вполне поддается выявлению и математической фиксации.
Прежде чем рассмотреть предложенные д'Аламбером критерии равномерности, которые позволяют выделить пригодные для измерения времени равномерные процессы, кратко остановимся на посленьютоновской эволюции идеи абсолютного времени классической физики. Это позволит нам более адекватно оценить даламберовские критерии и раскрыть их истинное значение в развитии представлений о времени.
Сформировавшаяся еще в конце средневековья и на протяжении трех столетий господствовавшая в сознании естествоиспытателей идея "математического времени" как некоторой абстрактной абсолютно равномерной независимой переменной, используемой при расчетах движений небесных тел, в ньютоновской механике обретает субстанциальность и превращается в некую реально существующую и равномерно текущую сущность. Но вместе с тем, хотя между "математическим временем" доньютоновской астрономии и механики и абсолютным временем ньютоновских "Начал" и существует определенная генетическая связь, тем не менее усвоение идеи абсолютного времени, равно как и самих "Начал", несомненно, потребовало от исследователей определенных усилий и достаточно длительного времени. Формальное сходство "математического времени" доньютоновской астрономии и механики с абсолютным временем ньютоновских "Начал" создают иллюзию легкости и беспроблемности для естествоиспытателей XVII века усвоения ньютоновских представлений о времени50. Только в работах тех великих последователей И. Ньютона, которые проявили себя не только как естествоиспытатели, но и как философы, задумывавшиеся о содержании и сущности исходных понятий естествознания, можно уловить коллизии протекавшего на протяжении, по крайней мере, первой половины XVII века процесса утверждения ньютоновской концепции времени.
Как мы показали во второй главе, характерный для естествознания феноменологический подход к времени лишь как к количественной мере движения в сущностном, онтологическом плане дополнялся различного рода философскими и теологическими концепциями, характерной особенностью которых была тенденция субъективизации времени. Поэтому естествоиспытатели, которые не только восприняли ньютоновскую концепцию времени, но и стремились ее обосновать и утвердить, были вынуждены обратить особое внимание на проблему объективности времени.
Так, Леонард Эйлер (1707-1783) в "Механике" (1736) и в "Теории движения твердых тел" (1765) отстаивает идею абсолютно равномерного временного течения и, не называя имен, полемизирует с теми, кто субъективирует время.
У Л. Эйлера сохраняются и некоторые элементы традиционных представлений о времени. В частности, он считает, что человек обладает внутренним, безотносительным к наблюдаемым движениям чувством времени и способностью интуитивно определять равенство различных интервалов длительности. Он пишет, что “если бы у нас, как некоторые склонны думать, не было других средств для определения времени, кроме как из рассмотрения движения, то мы не могли бы признать ни времени без движения, ни движения без времени...” /Эйлер, 1938, с. 278/. Правда, Эйлер отмечает, что делить время мы научились от наблюдений за движением Солнца, но “и без помощи движения мы имеем представление о том, что такое до и после, а отсюда, по-видимому, само собой вытекает понятие последовательности” /Там же/. И хотя более детальным познанием времени мы обязаны рассмотрению движения, “отсюда еще не следует, что время само по себе представляет собой не что иное, как лишь то, что мы воспринимаем. Что представляют собой два равных промежутка времени, это понимает всякий, хотя бы в течение этих промежутков, может быть, и не произошло равных изменений, на основании которых можно было бы прийти к заключению о равенстве этих промежутков времени” /с. 279/.
Вместе с тем Эйлер считает, что “деление времени на части не является чисто умственной операцией, как обыкновенно утверждают те, которые помещают время только в нашем сознании, не отделяя понятия времени от самого времени.
В самом деле, если бы время представляло собой не что иное, как последовательность наступающих друг за другом явлений, и если бы вне нашего сознания не существовало никаких средств для измерения времени, то нам ничто не мешало бы при всяком движении считать равными те части времени, в течение которых проходятся равные пути, так как они кажутся следующими друг за другом через равные промежутки. Следовательно, мы могли бы с одинаковым основанием рассматривать любое движение как равномерное. Однако сама природа вещей достаточно убедительно свидетельствует, что равномерное движение существенно отличается от неравномерного; следовательно, равенство промежутков времени, на котором это основывается, представляет собой нечто большее, чем содержание наших понятий” /с. 284-285/.
Здесь мы наблюдаем, фактически, стремление сочетать представление о времени как о некоторой абстракции от наблюдаемых движений с ньютоновской идеей абсолютного времени.
Развернувшаяся в конце XIX - начале XX вв. критика идеи абсолютного времени классической физики раскрыла несостоятельность представлений о времени как о некоторой самостоятельной равномерно текущей сущности. Однако в период становления и поступательного развития ньютоновской механики даже основоположники позитивизма О. Конт (1798-1857) и Г. Спенсер (1820-1903) не смогли разглядеть в ньютоновских абсолютных пространстве и времени ненавистных им априорных метафизических сущностей. И хотя основоположники позитивизма чувствуют и понимают всю сложность интерпретации понятий пространства и времени, тем не менее им кажется, что за априорными метафизическими идеями абсолютных пространства и времени классической физики скрывается некая реальность.
Так, например, Г. Спенсер считает, что наше сознание непосредственно свидетельствует о том, что “пространство и время существуют не в мысли, а вне ее и столь абсолютно не зависят от нее, что их нельзя понять, как переставшими существовать даже в том случае, если ум перестал существовать” /Спенсер, т.1, с. 28/. Правда, пространство и время как таковые не могут быть познаны ни как сущности, ни как атрибуты сущностей. Они познаются лишь в отношении к сознанию. Время - это абстракт отношения последовательности, а пространство - абстракт отношения сосуществования /с. 93/. При этом понятия пространства и времени, как и другие абстрактные понятия, образуются из отдельных конкретных фактов, но их отличие “состоит в том, что, в данном случае, систематизация опыта прошла через всю эволюцию мышления” /с. 93/.
Что касается критики ньютоновских концепций пространства и времени со стороны Лейбница и Канта, то, как отмечает У.И. Франкфурт /Франкфурт, 1978, с. 157/, эта критика, не имея под собой достаточных оснований для физической дискуссии, осталась на чисто философском уровне и не оказала сколь-либо заметного влияния на сознание естествоиспытателей. В результате ньютоновская идея абсолютного времени вплоть до конца XIX столетия оказывается единственной научной концепцией и в сознании естествоиспытателей настолько естественной, самоочевидной, не требующей никакого обсуждения и обоснования, что становится возможным строить всю аналитическую механику, а в дальнейшем и все другие разделы физики без какого бы то ни было обсуждения свойств и сущности времени51.
Ньютоновское представление о времени на протяжении более чем 200 лет оставалось незыблемым как среди естествоиспытателей, так и среди значительной части философов. Правда, в философии параллельно развивались и иные, в частности кантианские, взгляды на время, но до конца XIX столетия они не оказывали заметного влияния на развитие естествознания.
К концу XIX века “механика, идущая по своему победоносному пути в разрешении различных проблем по естествознанию, достигает своего апогея” /Жуковский, 1937, т. IX, с. 245/, и в своем стремлении всяческому физическому явлению давать механическое толкование останавливается перед объяснением некоторых накопленных в физике опытных данных. Возникает необходимость приложить начала классической механики “не к простейшим элементам механики - силе и массе, а к различным физическим элементам: магнитному полюсу, элементу тока, наэлектризованному шарику, электрону, квантам и т.д.” /Там же/. Трудности в объяснении накопленных в физике фактов наводят исследователей на мысль, что возможно они не могут быть объяснены с помощью начал классической механики и что для их объяснения нужны некоторые видоизменения этих начал /Там же/.
В этот период начинает осознаваться абстрактность понятий абсолютного пространства и времени; вновь становятся актуальными проблемы измерения времени, определения одновременности пространственно удаленных друг от друга событий и т.д. До естествоиспытателей доходит, наконец, и кантианская критика исходных ньютоновских понятий классической физики. Так, Г.Р. Герц (1857-1894) предпринимает попытку изложить механику, исходя из кантианских представлений о пространстве и времени (См: /Герц, 1959/).
Критический анализ ньютоновских представлений о пространстве и времени одним из первых среди естествоиспытателей начал Эрнст Мах (1838-1916).
Э. Мах отмечает, что равномерное движение - это такое движение, при котором одинаковые приращения пройденного телом пути соответствуют равным изменениям другого тела, служащего в качестве эталона (например, вращение Земли). “Вопрос, равномерно ли движение само по себе, не имеет никакого смысла. В такой же мере мы не можем говорить об "абсолютном времени" (независимо от всякого изменения). Это абсолютное время не может быть измерено никаким движением, и поэтому не имеет никакого ни практического, ни научного значения; никто не вправе сказать, что он что-нибудь о таком времени знает, это праздное "метафизическое" понятие” /Мах, 1909, с. 187/.
Идею абсолютного времени подверг критике Анри Пуанкаре (1854-1912). Он пишет, что у человека нет непосредственной интуиции равенства двух промежутков времени, и мы не можем быть уверены в равенстве длительности повторяющихся процессов..
При измерении времени такими движениями, как качания маятника, считает Пуанкаре, мы принимаем постулат, согласно которому “длительность двух идентичных явлений одна и та же; или, если угодно, что одни и те же причины требуют одного и того же времени, чтобы произвести одни и те же действия” /Пуанкаре, 1990, с.222/. Однако, пишет он далее, следует быть осторожными. “Не может ли случиться так, что в один прекрасный день опыт опровергнет наш постулат?” /Там же/. Подводя итоги обсуждению проблемы измерения времени, А. Пуанкаре делает вывод, что отсутствующую у нас интуицию равенства двух промежутков времени мы заменяем некоторыми правилами, которые мы выбираем “не потому, что они истинны, а потому, что они наиболее удобны...” /с. 232/.
Не раскрыл природу равномерности и Альберт Эйнштейн (1879-1955).
В специальной теории относительности (СТО) предполагается, что в каждой точке пространства локальное время течет равномерно, и это фиксируется расположенными в этих точках вполне идентичными часами. Для того чтобы синхронизировать часы, находящиеся в разных точках пространства, достаточно обменяться между этими точками сигналами, фиксируя моменты посылки сигнала, скажем, из точки А в точку В, отражения его в точке В и возвращения в точку А. Иными словами, под синхронизацией часов в СТО понимается установка для них некоторого нуль-пункта, а не выверка разности их хода. Последнее не требуется в силу того, что в СТО предполагается обусловленная равномерностью течения локального времени одинаковость хода идентичных часов в разных точках одной и той же инерциальной системы отсчета. Правда, ход часов меняется при ускоренных движениях, поэтому "расставлять" часы в инерциальной системе отсчета следует с большой осторожностью, а еще лучше предполагать (что обычно и делается), что идентичные часы изначально расположены в каждой точке инерциальной системы отсчета и не совершали никаких перемещений в пространстве.
В общей теории относительности (ОТО) ход часов в каждой точке пространства зависит от силы гравитационного поля, поэтому проблема равномерности времени становится значительно более сложной. В ОТО, несмотря на зависимость метрики времени от силы гравитационного поля, приходится считать, что в каждой точке пространства время течет равномерно. При этом предполагается, что если бы вдруг во всем пространстве исчезло гравитационное поле, то расположенные в каждой точке пространства часы стали бы идти одинаково.
Однако на чем основана подобная уверенность в том, что расположенные в разных точках пространства часы могут идти одинаково? По-видимому, только на одинаковости их устройства и изготовления (См, например: /Сивухин, 1989, с. 25/). Иными словами, предполагается, что длительность идентичных явлений одна и та же /А. Пуанкаре/. Правда, А. Пуанкаре, высказывая сомнение по поводу такого постулата, имел в виду представление об абсолютной истинности этого постулата, тогда как в СТО и ОТО, казалось бы, указаны границы его истинности и выявлены факторы, от которых зависит истинность этого утверждения. Но тем не менее и в СТО остается нераскрытой природа равномерности времени и, в частности, одинаковости хода "идентичных" часов в разных точках одной и той же инерциальной системы отсчета.
Вопрос о природе равномерности времени оказался настолько сложным, что и по сей день остается нерешенным. Поэтому неудивительно, что и сегодня многие исследователи считают, что "равномерность" не имеет под собой никакой объективной основы и что "равномерность" - это такое свойство эталонных часов, а следовательно и отмеряемого этими часами времени, которое устанавливается соглашением52.
Разумеется, мы можем договориться считать равными интервалы времени между последующими повторениями любого повторяющегося процесса. Так, используя пример Р. Карнапа /Карнап, 1971/, мы можем по договоренности считать, что мистер Смит выходит из дома через равные интервалы времени, и по его выходам из дома измерять время. Вопрос только в том, какова ценность подобного способа измерения. Не следует, видимо, забывать, что у А. Пуанкаре под "удобством" того или иного способа измерения времени имеется в виду не бытовая комфортность приемов и методов процесса измерения, а степень простоты формулировок законов физики, механики и астрономии, которую обеспечивают эти способы измерения времени (См. :/Пуанкаре, 1990, с. 232/). Это не только общеизвестно, но и общепринято. Даже те авторы, которые считают, что равномерность эталонных часов устанавливается по соглашению, далеко не произвольным образом выбирают эталонные часы, а сохраняют в качестве эталонных именно те, которые уже отобраны человечеством на практике и которые как раз и обеспечивают наиболее простую "формулировку естественных законов" природы /А. Пуанкаре/. При этом, однако, удивительным образом не замечается то обстоятельство, что "часами", обеспечивающими подобного рода "удобство", неизменно являются движения или процессы, относящиеся к обширному классу "равномерных" движений и процессов, которые, как писали Л. Эйлер и Ж.-Л. д’Аламбер, по самой их природе весьма существенно отличаются от неравномерных.
Ж.-Л. д’Аламбер указал на одно очень важное свойство именно равномерных движений, заключающееся в том, что отношение расстояний, пройденных двумя равномерно движущимися телами за один и тот же интервал времени, оказывается величиной постоянной для любых произвольно выбранных (не равных нулю) интервалов длительности.
Однако этот критерий равномерности многими исследователями не принимается во внимание. Это объясняется тем, что до сих пор остается невыясненной природа равномерности, и равномерность сохраняет статус интуитивно понятного и не требующего объяснения свойства времени. При этом, как мы видели, до сих пор широкое распространение имеет представление о том, что равномерность - это вовсе не объективное свойство времени, а чисто условное, которое мы приписываем тем движениям или процессам, которые выбрали в качестве эталонных (основных) часов и по которым градуируются все остальные часы. Однако если принять последнюю точку зрения, то становится непонятной проблема точности измерения времени, успешным решением которой не без оснований гордится современная наука53. Действительно, что означает точность измерения времени, если можно договориться считать равномерным любой процесс и сделать его эталонным? В этом случае под точностью измерения времени придется понимать только то, насколько точно часы, которыми мы пользуемся, воспроизводят ход наших эталонных часов и ничего более. Вместе с тем реальное положение дел в области измерения времени совершенно не допускает подобного произвола.
Таким образом, вопрос о природе равномерности времени и критериях, при помощи которых можно выявлять пригодные для измерения времени равномерные процессы, по сей день остается актуальным.
Д'Аламбер, как и Ньютон, считал, что “время по своей природе течет равномерно” /Даламбер, 1950, с. 19/, но поскольку мы не можем непосредственно воспринимать время, то вынуждены для его измерения прибегать к чувственно воспринимаемым движениям, причем для этой цели в принципе пригодны любые, в том числе и неравномерные движения. Однако, замечает д’Аламбер, “при помощи неравномерного движения невозможно было бы измерять время, не зная откуда-нибудь заранее, какая связь между отношением времен и отношением пройденных путей соответствует данному движению” /Там же, с.46/. Для того, чтобы использовать неравномерное движение для измерения времени, необходимо знать уравнение этого движения, которое можно рассматривать как уравнение, выражающее “не соотношение между пространством и временем...”, а “соотношение между отношением частей времени к единице времени и отношением частей пройденного пространства к единице пространства” /Там же, с.19/. Но уравнение движения, отмечает д’Аламбер, мы можем знать только из опыта, который предполагает, “что уже имеется вполне определенная мера времени” /Там же, с.46/.
Поэтому для измерения времени мы должны искать “такой частный вид движения, при котором связь между отношением промежутков времени и отношением пройденного пути известна независимо от каких бы то ни было допущений, а просто в силу природы самого движения” /Там же, с.45/. А поскольку “длительность или продолжительность существования вещей одна и та же, быстры ли движения (по которым измеряется время), медленны ли, или их совсем нет...” /Ньютон, 1989, с.32/, то искомый частный вид движения должен быть единственным, обладающим указанным выше свойством. “Обоим этим условиям (т.е. требованию априорной известности уравнения движения и условию единственности. - И.Х.) удовлетворяет только равномерное движение” /Даламбер, 1950, с.45/.
“В самом деле, - рассуждает д’Аламбер, - движение тела само по себе будет равномерным...: ускоренным или замедленным оно становится лишь при действии той или иной внешней причины, и тогда это движение может подчиняться бесчисленному множеству законов изменения. Закон равномерности, т.е. равенство отношения между промежутками времени и отношения между пройденными путями, является свойством этого движения, взятого само по себе. Поэтому равномерное движение имеет наибольшее соответствие с длительностью, и вследствие этого оно наиболее пригодно служить мерой этой длительности, поскольку части последней следуют одна за другой также неизменно и равномерно. Напротив, всякий закон ускорения или замедления движения, так сказать, произволен и зависит от внешних обстоятельств. Неравномерное движение не может быть, поэтому, естественной мерой времени” /Там же, с.46/.
Каким же образом убедиться в том, что данное движение является абсолютно равномерным? Вслед за Ньютоном, который предполагал, что, может быть, и “не существует (в природе) такого равномерного движения, которым время могло бы измеряться с совершенною точностью” /Ньютон, 1989, с.32/, д’Аламбер также склоняется к мысли, что, видимо, нельзя найти в точности равномерного движения. “Но, - пишет он, - отсюда вовсе не следует, что равномерное движение не является по своей природе единственной первичной и простейшей мерой времени. Если у нас нет возможности найти точную и строгую меру времени, то мы должны искать, по крайней мере, приближенную меру, - среди движений примерно равномерных” /Там же, с.46/.
Таким образом, "равномерность" рассматривается д'Аламбером как абсолютное свойство некоторого единственного класса движений, в силу чего все наблюдаемые процессы предполагается возможным однозначно разбить на "равномерные" (или, по крайней мере, "приближенно равномерные") и неравномерные. Поэтому мы вправе ожидать, что даламберовские критерии равномерности помимо разделения всех движений на "равномерные" и "неравномерные", позволяют обеспечить также однозначность подобного разбиения.
Приступая к анализу предлагаемых Ж. д'Аламбером трех способов определения равномерности тех или иных движений, мы должны особо подчеркнуть, что все способы предполагают сравнение между собой двух или нескольких движений (процессов). Эта особенность даламберовских критериев далеко не случайна. Дело в том, что если нам дан один единственный процесс, то мы ничего не сможем сказать о его равномерности или неравномерности, поскольку для этого должны будем сравнивать между собой периоды времени, на протяжении которых наблюдаемая нами система изменяется одинаковым образом. Но эти периоды времени невозможно сравнивать между собой непосредственно, поскольку они следуют друг за другом во времени. Для решения нашей задачи мы должны были бы иметь некоторый "хранитель длительности", т.е. некоторые "часы", при помощи которых можно было бы сравнивать различные интервалы длительности. Но подобный "хранитель длительности" сам должен быть некоторым процессом, что противоречит нашему условию. Следовательно, вопрос о равномерности или неравномерности тех или иных процессов правомерен лишь в том случае, если мы имеем возможность сравнивать исследуемый процесс с другими материальными процессами. В этом случае мы можем воспользоваться следующим критерием равномерности:
“...Движение можно считать приближенно равномерным, когда мы, сравнивая его с другими движениями, замечаем, что все они управляются одним и тем же законом. Так, если несколько тел движутся таким образом, что пути, проходимые ими за одно и то же время, всегда находятся (точно или приближенно) в одном и том же отношении друг к другу, то считают движение этих тел равномерным или по меньшей мере весьма близким к равномерному” /Даламбер, 1950, с.47/. И далее д’Аламбер следующим образом поясняет эту мысль.
Пусть мы имеем равномерно движущееся тело А, которое за произвольно взятый промежуток времени Т проходит путь Е, а другое тело В, которое также движется равномерно, за тот же промежуток времени проходит расстояние е. “Тогда независимо от того, одновременно ли начали двигаться эти два тела или нет, отношение Е к е будет всегда одним и тем же. И этим свойством обладает лишь равномерное движение” /Там же, с.47/.
Однако нетрудно заметить, что если все равномерные движения одновременно (независимо от того, когда началось то или иное движение) ускоряются или замедляются по одному и тому же закону, то и числитель, и знаменатель отношения Е/е будут умножаться на одну и ту же (постоянную или переменную) величину и отношение останется неизменным (разумеется, при вполне естественном предположении, что рассматриваемые коэффициенты ускорения или замедления движения не обращаются в нуль). Поэтому рассуждения д'Аламбера будут справедливы лишь в том случае, если сравниваемые движения не могут одновременно и совершенно одинаковым образом изменять свои скорости. Если же предположить, что наблюдаемые процессы взаимосвязаны (скажем, через какие-то фундаментальные законы той или иной формы движения материи, к которой относятся сравниваемые процессы, или в силу принадлежности сравниваемых процессов к некоторой единой целостной системе, либо в силу каких-то иных причин) и совершенно одинаковым образом изменяют свои скорости, то мы должны прийти к выводу, что рассматриваемый критерий равномерности не дает возможности выделить из всего многообразия материальных процессов "истинно" равномерные, а лишь указывает на соравномерность сравниваемых процессов, т.е. на то, что данные процессы подчиняются одному и тому же (или одним и тем же) закону (или законам) и синхронно изменяют свои скорости одинаковым образом.
Не позволяют установить "абсолютную равномерность" и два других предлагаемых д'Аламбером критерия равномерности.
Согласно одному из них, “...движение тела можно считать приближенно равномерным в том случае, если тело проходит одинаковые пути за такие промежутки времени, которые мы можем считать одинаковыми. Промежутки же времени мы можем считать одинаковыми в том случае, если многократные наблюдения показывают, что в течение их происходят одинаковые события, которые можно считать длящимися одинаково. Так, мы можем считать, что из одной и той же клепсидры вода вытекает всякий раз за одно и то же время” /Там же, с.47/.
Для того чтобы применять этот критерий равномерности, надо быть уверенным, что существуют процессы, протекающие всякий раз одинаково, при помощи которых можно отождествлять удаленные друг от друга (во времени) временные интервалы. Однако вывод о том, что данный процесс всякий раз протекает одинаково, опирается на наш повседневный опыт и основан, в конечном итоге, на сравнении этого процесса с другими. Но какова гарантия того, что сравниваемые процессы не связаны между собой какими-либо не известными нам фундаментальными законами природы и не входят в один и тот же класс соравномерных процессов?
Аналогичное возражение можно высказать и по отношению к третьему критерию равномерности, согласно которому “...движение можно считать приближенно равномерным, когда мы вправе полагать, что действие ускоряющей или замедляющей причины - если таковая имеется, - может быть только неощутимой” /Там же, с.47/.
Однако, в общем случае, о наличии или отсутствии подобных причин мы можем судить лишь по результатам их действия, т.е. по реальному ускорению или замедлению наблюдаемого движения или процесса, что также требует сопоставления исследуемых объектов с объектами, которые, по нашему мнению, либо не претерпевают никаких изменений, либо одинаковые изменения всякий раз длятся одинаково. Но в таком случае все те причины, которые одинаково ускоряют или замедляют все сравниваемые процессы, останутся для нас "неощутимыми".
Таким образом, предложенные Ж. д'Аламбером критерии равномерности основаны на сравнении двух или нескольких процессов между собой и позволяют установить лишь их соотносительную равномерность, т.е. равномерность их относительно друг друга.
Рассмотрим теперь предложенный Рудольфом Карнапом (1891-1970) способ выделения пригодных для измерения времени строго периодических процессов.
Обсуждая вопрос о способах измерения времени, Р. Карнап обращается к периодическим процессам, среди которых различает "слабые периодические процессы", такие, как выходы мистера Смита из дома, пульс человека и т.п., т.е. процессы, у которых периоды могут каким-то образом изменяться, и "сильные периодические процессы", у которых периоды сохраняются постоянными. Для измерения времени желательно было бы взять такой периодический процесс, периоды которого всегда оставались бы неизменными. Но если мы еще не умеем измерять время, то мы и не можем априори сказать, какие периодические процессы относятся к слабым, а какие - к сильным. С целью выделения последних Р. Карнап вводит понятие эквивалентности периодических процессов. Он пишет: “Если мы обнаружим, что некоторое число периодов процесса ![]() всегда соответствует определенному числу периодов процесса
всегда соответствует определенному числу периодов процесса ![]() , тогда мы говорим, что эти два периодических процесса эквивалентны” /Карнап, 1971, с.133/.
, тогда мы говорим, что эти два периодических процесса эквивалентны” /Карнап, 1971, с.133/.
Нетрудно заметить, что это условие эквивалентности периодических процессов тождественно первому условию равномерности д'Аламбера. Только в случае периодических процессов вместо пройденных путей Е и е мы берем числа периодов ![]() и
и ![]() и требуем, как и д'Аламбер, чтобы отношение этих величин, т.е.
и требуем, как и д'Аламбер, чтобы отношение этих величин, т.е. ![]() , оставалось постоянным на любых произвольных интервалах времени -
, оставалось постоянным на любых произвольных интервалах времени - ![]() . Поэтому эквивалентные периодические процессы можно было бы назвать "равномерными периодическими процессами"54.
. Поэтому эквивалентные периодические процессы можно было бы назвать "равномерными периодическими процессами"54.
Общепринятый способ измерения времени Р. Карнап считает основанным на том, что эмпирически выявлен большой класс эквивалентных периодических процессов, каждый из которых может быть использован для измерения времени. К этому классу относятся вращательные движения небесных тел, колебания маятников, движения балансирных колесиков часов и др. При этом Р. Карнап замечает, что, “насколько мы знаем, существует только один обширный класс такого рода” /Там же, с.133. Подчеркнуто Р. Карнапом/. Если это замечание истинно и существует только один класс эквивалентных процессов (что соответствует утверждению Ж. д’Аламбера о существовании единственного класса равномерных движений), то должна существовать единственная метрика времени, связанная с этим единственным классом эквивалентных процессов. Вопрос об эквивалентности (или равномерности) тех или иных процессов оказывается правомерным лишь в том случае, когда мы имеем возможность сравнивать исследуемый процесс с другими процессами. Это наводит на мысль о том, что в принципе возможны различные группы соравномерных (или периодических эквивалентных) процессов, т.е. таких, которые в силу каких-то причин (например, в силу подчинения общим законам, принадлежности единой целостной системе и т.д.) изменяются совершенно одинаковым образом; поэтому, сравнивая эти процессы друг с другом, мы должны будем убеждаться в том, что они "равномерны" (или "эквивалентны"). Но при сравнении друг с другом процессов, принадлежащих к разным группам соравномерных (или эквивалентных) процессов, мы будем обнаруживать, что они между собой не соравномерны (не эквивалентны). В этом случае должна появиться возможность (а в определенных ситуациях и необходимость) введения различных временных метрик.
Некоторые свойства подобных классов соравномерных и периодических эквивалентных процессов можно исследовать при помощи следующего мысленного эксперимента.
- Представим себе, что на плоской, достаточно широкой и неограниченно длинной ленте нанесена декартова система координат с осью абсцисс, направленной вдоль, и осью ординат - поперек ленты. Лента изготовлена из идеально эластичной пленки и может, не образуя складок и не разрываясь, неограниченно сжиматься и растягиваться вдоль оси абсцисс, оставаясь неизменной вдоль оси ординат, т.е. растяжения и сжатия пленки представляют собой непрерывное взаимнооднозначное (гомеоморфное) отображение, при котором на континууме числовой оси (оси абсцисс) не исчезают существующие и не возникают новые точки, а также не меняется порядок их следования вдоль оси. Пленка, из которой сделана лента, может находиться и в фиксированном, как бы "замороженном", состоянии, когда она полностью теряет свою эластичность и становится абсолютно жесткой, недеформируемой;
- Представим далее, что мы зафиксировали ("заморозили") ленту в некотором исходном состоянии, нанесли на ось абсцисс равномерную шкалу (назовем ее q-шкалой) и, используя ее как шкалу времени, нанесли на ленту множество самых различных графиков, считая деления на оси ординат шкалами некоторых изменяющихся во времени величин. При этом пусть графики ![]() представляют собой графики равномерных,
представляют собой графики равномерных, ![]() - периодических и графики
- периодических и графики ![]() - более сложных и в том числе стохастических функций равномерного аргумента q;
- более сложных и в том числе стохастических функций равномерного аргумента q;
- Представим теперь, что лента "разморожена" и по всей длине оси абсцисс деформирована так, что в каждой точке этой оси коэффициент деформации является случайной величиной. После этого мы снова зафиксировали ("заморозили") ленту, на ось абсцисс нанесли новую равномерную шкалу (назовем ее r-шкалой) и,используя ее как шкалу равномерного времени, нанесли на ленту новое множество графиков, среди которых графики ![]() представляют собой графики равномерных,
представляют собой графики равномерных, ![]() - графики периодических и
- графики периодических и ![]() - графики более сложных и в том числе стохастических функций равномерной переменной r;
- графики более сложных и в том числе стохастических функций равномерной переменной r;
- Предположим, что мы большое число раз проделали описанные выше операции "замораживания" и "размораживания" пленки и каждый раз наносили на ленту новые множества графиков, среди которых были как равномерные, так и периодические и более сложные функции наносимых каждый раз на ось абсцисс равномерных переменных. Обозначим последнюю нанесенную на ось абсцисс шкалу как шкалу t-времени, а графики равномерных функций обозначим ![]() , графики периодических функций -
, графики периодических функций - ![]() и графики более сложных функций -
и графики более сложных функций - ![]() ;
;
- И, наконец, представим себе, что все нанесенные на ось абсцисс шкалы исчезли или настолько перепутались, что мы ими воспользоваться не можем; что у нас нет никакой линейки, при помощи которой можно было бы установить равенство различных отрезков на оси абсцисс; что мы не знаем, в каком состоянии находится наша пленка, и нам неизвестно, подвергалась ли она каким-либо сжатиям и растяжениям после того, как были нанесены последняя равномерная t-шкала и последнее множество графиков.
Спрашивается: можно ли каким-то образом восстановить на оси абсцисс равномерную шкалу?
Для ответа на этот вопрос попытаемся воспользоваться критерием эквивалентности строго периодических процессов Р. Карнапа.
Итак, на ленте имеется огромное количество различных графиков, которые после их нанесения на ленту многократно деформировались вместе с лентой. Хотя мы не можем априори установить, какие графики и когда были нанесены - в этом отношении графики для нас неразличимы, - тем не менее для удобства рассуждений сохраним их обозначения, пометив только штрихами в знак того, что исследуемые графики отличаются от исходных в силу тех деформаций, которые испытала пленка после нанесения на нее каждого очередного множества графиков. Итак, мы имеем графики:
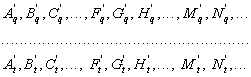
Поскольку мы не можем непосредственно отличить "сильные" периодические процессы от "слабых", то выделим из множества графиков графики всех повторяющихся процессов, т.е. таких, у которых изменяющиеся параметры с большей или меньшей регулярностью возвращаются к одним и тем же значениям. В эту группу попадут графики как всех строго периодических функций, обозначенных ![]() , так и графики повторяющихся, но не строго периодических, а “более сложных” функций, обозначенных литерами M, N и т.д.
, так и графики повторяющихся, но не строго периодических, а “более сложных” функций, обозначенных литерами M, N и т.д.
Теперь на произвольно выделенных отрезках оси абсцисс будем подсчитывать число повторений (максимумов, или минимумов, или точек перемены знака функции от минуса к плюсу или наоборот) выделенных нами повторяющихся функций. Пусть для i-го произвольного отрезка ![]() оси абсцисс число таких повторений указанных функций будет
оси абсцисс число таких повторений указанных функций будет
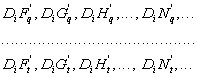
Если мы рассмотрим системы попарных отношений этих величин для большого числа произвольных отрезков ![]() оси абсцисс, то обнаружим, что среди всего множества повторяющихся процессов имеются различные их группы, удовлетворяющие условию эквивалентности, а именно те, в обозначениях которых имеются индексы q, ..., t.
оси абсцисс, то обнаружим, что среди всего множества повторяющихся процессов имеются различные их группы, удовлетворяющие условию эквивалентности, а именно те, в обозначениях которых имеются индексы q, ..., t.
Действительно, по самому характеру нанесения на ленту соответствующих групп графиков и последующей деформации ленты можно утверждать, что если на некотором отрезке оси абсцисс при нанесении графиков помещалось ![]() периодов ("повторений") одной периодической функции и
периодов ("повторений") одной периодической функции и ![]() периодов ("повторений") другой, то при любых деформациях пленки отрезок оси абсцисс, содержащий
периодов ("повторений") другой, то при любых деформациях пленки отрезок оси абсцисс, содержащий ![]() повторений первой функции, будет содержать
повторений первой функции, будет содержать ![]() повторений второй функции.
повторений второй функции.
Аналогичным образом можно было бы воспользоваться и первым критерием равномерности д’Aламбера, который гласит, что отношение приращений двух равномерных функций есть величина постоянная для любых интервалов времени. Но с этой целью нам пришлось бы выделить группу монотонных функций ![]() , и рассмотреть множество попарных отношений приращений этих функций на произвольных отрезках
, и рассмотреть множество попарных отношений приращений этих функций на произвольных отрезках ![]() оси абсцисс. Поскольку пленка деформируется только вдоль оси абсцисс, то при любых деформациях для каждой группы монотонных функций с индексами q, ... , t мы найдем, что характерное для них в момент нанесения графиков на пленку свойство равенства отношений их приращений за произвольные интервалы равномерного времени сохранится и после деформации.
оси абсцисс. Поскольку пленка деформируется только вдоль оси абсцисс, то при любых деформациях для каждой группы монотонных функций с индексами q, ... , t мы найдем, что характерное для них в момент нанесения графиков на пленку свойство равенства отношений их приращений за произвольные интервалы равномерного времени сохранится и после деформации.
Действительно, если в исходном состоянии пленки, когда на нее только что нанесена очередная группа графиков, на произвольных отрезках ![]() оси абсцисс две равномерные функции А и B имели приращения
оси абсцисс две равномерные функции А и B имели приращения ![]() и их попарные отношения на любых интервалах оси абсцисс оставались равными, т.е.
и их попарные отношения на любых интервалах оси абсцисс оставались равными, т.е.
![]() ,
,
то после всех деформаций пленки на тех интервалах оси абсцисс, на которых первая функция имеет рассмотренные выше приращения ![]() , вторая функция будет иметь те же приращения
, вторая функция будет иметь те же приращения ![]() , которые мы имели до деформации пленки, в силу чего их отношения также останутся константами.
, которые мы имели до деформации пленки, в силу чего их отношения также останутся константами.
Полученные результаты означают, что равномерную шкалу времени на оси абсцисс можно восстановить выбрав в качестве строго периодического процесса один из эквивалентных процессов, выявленных либо среди периодических процессов ![]() , либо - процессов
, либо - процессов ![]() и т.д., либо, наконец, среди процессов
и т.д., либо, наконец, среди процессов ![]() .
.
Если в качестве единицы измерения времени мы выберем периоды, скажем, функции ![]() , то получим некоторую равномерную шкалу (назовем ее q-шкалой), состоящую из точек ..., q[-j],..., q[-1], q[0], q[1], ,..., q[i],..., где расстояния между соседними точками равняются периодам функции
, то получим некоторую равномерную шкалу (назовем ее q-шкалой), состоящую из точек ..., q[-j],..., q[-1], q[0], q[1], ,..., q[i],..., где расстояния между соседними точками равняются периодам функции ![]() (точнее, функции
(точнее, функции ![]() , поскольку периоды функции
, поскольку периоды функции ![]() мы считаем равными). При этом восстановится равенство периодов (с некоторой степенью точности) и всех эквивалентных
мы считаем равными). При этом восстановится равенство периодов (с некоторой степенью точности) и всех эквивалентных ![]() , но более долгопериодических функций. Однако восстановление равенства периодов процесса
, но более долгопериодических функций. Однако восстановление равенства периодов процесса ![]() не обязательно должно вести к восстановлению равенства периодов более короткопериодических, чем
не обязательно должно вести к восстановлению равенства периодов более короткопериодических, чем ![]() функций, поскольку внутри каждого периода процесса
функций, поскольку внутри каждого периода процесса ![]() лента осталась деформированной. Иными словами, период процесса
лента осталась деформированной. Иными словами, период процесса ![]() (обозначим
(обозначим ![]() ) оказывается своего рода "далее неделимым квантом" времени, а восстановленное таким образом
) оказывается своего рода "далее неделимым квантом" времени, а восстановленное таким образом ![]() -время (точнее
-время (точнее ![]() -время)55 оказывается "точечным" "квантованным" временем. Мы можем "уплотнить" количество точек
-время)55 оказывается "точечным" "квантованным" временем. Мы можем "уплотнить" количество точек ![]() -времени, если в качестве единицы измерения возьмем период более короткопериодической, чем
-времени, если в качестве единицы измерения возьмем период более короткопериодической, чем ![]() , эквивалентной периодической функции.
, эквивалентной периодической функции.
Можно показать, что с переходом к ![]() -времени также точечно восстановится равномерность и всех тех равномерных функций, графики которых были начерчены на ленте до ее деформации.
-времени также точечно восстановится равномерность и всех тех равномерных функций, графики которых были начерчены на ленте до ее деформации.
Действительно, пусть до деформации ленты за время ![]() периодов процесса
периодов процесса ![]() равномерные функции
равномерные функции ![]() имели приращения
имели приращения ![]() ,
, ![]() ,
, ![]() , ..., а их попарные отношения
, ..., а их попарные отношения ![]() ,
, ![]() , ... ,
, ... , ![]() , ... оставались константами вдоль оси абсцисс. После деформации ленты и нанесения на ось абсцисс новой равномерной r-шкалы графики
, ... оставались константами вдоль оси абсцисс. После деформации ленты и нанесения на ось абсцисс новой равномерной r-шкалы графики ![]() стали в единицах r-времени графиками стохастических функций. Но поскольку при деформации ленты точки вдоль оcи ординат не смещались, то приращения функций
стали в единицах r-времени графиками стохастических функций. Но поскольку при деформации ленты точки вдоль оcи ординат не смещались, то приращения функций ![]() за те же
за те же ![]() "периодов" функции
"периодов" функции ![]() (ставшей теперь "слабой" периодической функцией, в терминологии Р. Карнапа) остались теми же, т.е.
(ставшей теперь "слабой" периодической функцией, в терминологии Р. Карнапа) остались теми же, т.е. ![]() ,
, ![]() ,
, ![]() , ... , и соответственно остались константами попарные отношения приращений этих функций за время произвольного числа
, ... , и соответственно остались константами попарные отношения приращений этих функций за время произвольного числа ![]() периодов функции
периодов функции ![]() . Не внесет изменений в приращения функций
. Не внесет изменений в приращения функций ![]() за те же К периодов функции
за те же К периодов функции ![]() и восстановление равенства периодов этой функции и переход таким образом к
и восстановление равенства периодов этой функции и переход таким образом к ![]() -времени.
-времени.
И наконец, следует заметить, что квантованностью и точечностью ![]() -времени можно будет пренебречь при описании процессов и явлений, совершающихся в достаточно больших временных масштабах, при которых
-времени можно будет пренебречь при описании процессов и явлений, совершающихся в достаточно больших временных масштабах, при которых ![]() , т.е. период эталонной функции
, т.е. период эталонной функции ![]() , станет "бесконечно малой" величиной.
, станет "бесконечно малой" величиной.
Что касается функций, графики которых были начерчены на ленте после ее деформации, то с переходом к ![]() -времени все эти функции станут стохастическими, поскольку восстановление равенства периодов процесса
-времени все эти функции станут стохастическими, поскольку восстановление равенства периодов процесса ![]() равносильно деформации пленки с коэффициентами, представляющими собой случайные величины, которые в точках ...,
равносильно деформации пленки с коэффициентами, представляющими собой случайные величины, которые в точках ...,![]() с точностью до постоянного множителя совпадают с коэффициентами первоначальной деформации пленки, но взятыми с обратными знаками.
с точностью до постоянного множителя совпадают с коэффициентами первоначальной деформации пленки, но взятыми с обратными знаками.
Если же для восстановления равномерной шкалы на оси абсцисс выберем один из эквивалентных процессов, обнаруженных, скажем, в группе ![]() , то так же точечно восстановим равномерную
, то так же точечно восстановим равномерную ![]() -шкалу. По построению нашей гипотетической модели мы знаем, что эта шкала непрерывная, но так как нам неизвестно, как строились графики, то вынуждены будем повторить все те рассуждения, которые были приведены в связи с восстановлением
-шкалу. По построению нашей гипотетической модели мы знаем, что эта шкала непрерывная, но так как нам неизвестно, как строились графики, то вынуждены будем повторить все те рассуждения, которые были приведены в связи с восстановлением ![]() -шкалы.
-шкалы.
Аналогичным образом можно было бы рассмотреть любые группы выявленных повторяющихся (квазипериодических) процессов с другими индексами и "восстановить" на оси абсцисс соответствующие равномерные шкалы.
Таким образом, мысленный эксперимент показал, что в принципе возможно реальное существование качественно различных, не сводимых друг к другу классов соравномерных процессов, которые относительно друг друга в общем случае выглядят как группы стохастических процессов.
Итак, равномерность представляет собой соотносительное свойство как минимум двух сопоставляемых между собой материальных процессов и в принципе возможно существование неограниченного множества классов соравномерных процессов. При этом "критерии равномерности", которыми мы можем воспользоваться, не позволяют ни один из этих классов выделить как класс "действительно", "истинно" или "абсолютно" равномерных процессов. Что касается вопроса о реальном существовании качественно различных, не сводимых друг к другу классов соравномерных процессов, то современная наука, фактически, уже дала на него положительный ответ. Именно такими специфическими классами являются протекающие в живых организмах определенные совокупности биологических процессов, что позволяет, используя единицы биологического времени, описывать процессы жизнедеятельности и развития живых организмов не как стохастические, каковыми они выглядят при описании их в общепринятых единицах физического времени, а как динамические процессы56.
Вместе с тем общепринято представление о том, что существует один единственный класс равномерных (и строго периодических) процессов, при помощи которых (с определенной степенью точности) можно измерять абсолютно равномерное время. У исследователей, кажется, вообще не возникает сомнений в том, что равномерность - это некоторое уникальное свойство равномерно текущей сущности - "времени" и что оно недоступно для непосредственного анализа, поскольку для этого потребовалось бы иметь какое-то другое равномерное время57.
Весьма серьезной основой для подобной абсолютизации свойства равномерности измеряемого общеизвестными способами времени является и то обстоятельство, что хронометрирование и теоретическое описание материальных процессов в единицах этого времени позволило человечеству раскрыть многие объективные законы природы и построить научные теории, которые достаточно адекватно отражают свойства объектов, процессов и явлений материальной действительности. Высокая познавательная эффективность измерения времени при помощи таких "равномерных" и "строго периодических" процессов, как вращение Земли вокруг оси и обращение ее вокруг Солнца, колебания физических маятников, кристаллических, молекулярных и атомных осцилляторов является достаточно веским аргументом в пользу предположения, что это действительно равномерные и строго периодические процессы, хотя никакими экспериментами подобные представления невозможно доказать.
Учитывая полученные результаты, мы можем утверждать, что перечисленные выше механические движения входят в один класс соравномерных процессов, представляющий собой материальную основу общеизвестного физического времени. В связи с этим возникает вопрос: что объединяет в один класс соравномерных процессов те материальные движения, при помощи которых обычно измеряется время?
50 Как отмечают исследователи истории становления и развития классической механики, процесс освоения естествоиспытателями ньютоновских "Начал" растянулся на несколько десятилетий, в течение которых развитие классической механики продолжалось без должного влияния этого гениального произведения (См.: /Погребысский, 1971, стр. 122; Франкфурт, 1978, стр. 158/). Это вполне понятно. Восприятие новых идей даже в современной динамично развивающейся науке требует подчас двух-трех десятилетий, т.е. времени творческой жизни поколения ученых (См.: /Кун, 1977/). В XVI-XVII вв. переходный период от старых идей к новым, несомненно, был значительно более продолжительным. При этом не следует забывать грандиозность масштабов научной революции XVI-XVII вв., важным элементом которой явилась разработка И. Ньютоном исходных понятий, принципов и математического аппарата классической физики.
51 В этом отношении характерна работа Ж.Л. Лагранжа (1736-1813) "Аналитическая механика" (1788), в которой автор, не обсуждая проблему времени и даже не определяя понятие времени, активно использует абсолютно равномерную независимую переменную "t".
52 Такую точку зрения, как мы уже отмечали (см. стр. 29), часто можно встретить в учебных пособиях по физике. См., например: /Сивухин, 1989, стр. 25/.
53 Вот какую таблицу эволюции точности измерения времени приводит Дж. Б. Мэрион /Мэрион, 1986, с. 12/:
Песчаные часы .....................................точность 1 секунда в 1.5 мин
Маятниковые часы................................ - " - 3 часа
Камертон................................................. - " - 1 сутки
Колебания кварцевого кристалла........ - " - 3 года
Резонатор молекулы аммиака............. - " - 30 лет
Цезиевый резонатор............................. - " - 30 тыс. лет
Водородный мазер............................... - " - 3 млн. лет
В настоящее время, как известно, в качестве эталонных часов используются часы, основанные на цезиевом резонаторе, а в будущем, видимо, придется перейти на часы, использующие в качестве стандарта равномерности частоту колебаний водородного мазера.
54 Строго говоря, не все эквивалентные периодические процессы являются равномерными. Как отметил еще Г. Галилей, равномерным является лишь такое движение, “при котором расстояния, проходимые движущимся телом в любые равные промежутки времени, равны между собой” /Галилей, 1964, с. 234/. При этом Галилей подчеркивает слово "любые", замечая, что возможны такие движения, когда тело в некоторые определенные равные промежутки времени будет проходить равные расстояния, тогда как в равные же, но меньшие части этих промежутков пройденные расстояния не будут равны /Там же/.
С этой точки зрения, вращение Земли вокруг оси - это действительно равномерный и вместе с тем ритмический процесс, тогда как качание физического маятника не является равномерным движением, поскольку маятник на протяжении каждого периода дважды останавливается, а между этими остановками движется с переменной скоростью. Поэтому, говоря об эквивалентных периодических процессах как о равномерных, мы не будем рассматривать их течение внутри отдельных периодов, а будем эти периоды считать далее неделимыми "квантами" данного периодического процесса. Именно в этом смысле все эквивалентные периодические процессы будут одновременно и "равномерными".
55 Поскольку мы не знаем первоначального масштаба q-шкалы и не можем его восстановить, то речь идет, разумеется, о восстановлении этой шкалы с точностью до некоторого масштабного коэффициента. Иными словами, q-шкала восстанавливается в том смысле, что восстанавливается равенство (конгруэнтность) периодов процесса ![]() , а не абсолютная величина этих периодов в единицах первоначальной q-шкалы.
, а не абсолютная величина этих периодов в единицах первоначальной q-шкалы.
56 Введенное нами понятие “класс соравномерных процессов” эквивалентен понятию “класс конгруэнтности”, используемому чаще применительно к пространственным расстояниям, чем к интервалам длительности (См.: /Грюнбаум, 1969/). В качестве примеров времен с несовместимыми классами конгруэнтности обычно указывают на введенные Милном t
- и t-времена, которые связаны между собой нелинейным отношением t
= ![]() (См.: /Miln, 1948, p/ 22/). Такое положение дел можно объяснить тем, что в длительности как одномерном многообразии разные классы конгруэнтности не позволяют развить особые математические теории времени (своего рода “хронометрии”) на подобии метрически разных геометрий трехмерного пространства. До сих пор разные классы конгруэнтности временных интервалов можно было вводить только при помощи тех или иных математических соотношений, связывающих новый класс конгруэнтности с конгруэнтностью интервалов длительности, устанавливаемых при помощи обычных часов. Эмпирическое же введение конгруэнтности временных интервалов казалось возможным только при помощи единственного в своем роде класса равномерных и строго периодических процессов. Однако теперь мы видим, что в принципе возможны разные классы конгруэнтности, связанные с реально существующими или, по крайней мере принципиально возможными в материальном тире классами соравномерных процессов.
(См.: /Miln, 1948, p/ 22/). Такое положение дел можно объяснить тем, что в длительности как одномерном многообразии разные классы конгруэнтности не позволяют развить особые математические теории времени (своего рода “хронометрии”) на подобии метрически разных геометрий трехмерного пространства. До сих пор разные классы конгруэнтности временных интервалов можно было вводить только при помощи тех или иных математических соотношений, связывающих новый класс конгруэнтности с конгруэнтностью интервалов длительности, устанавливаемых при помощи обычных часов. Эмпирическое же введение конгруэнтности временных интервалов казалось возможным только при помощи единственного в своем роде класса равномерных и строго периодических процессов. Однако теперь мы видим, что в принципе возможны разные классы конгруэнтности, связанные с реально существующими или, по крайней мере принципиально возможными в материальном тире классами соравномерных процессов.
57 Характерны в этом отношении рассуждения М.Д. Ахундова относительно парадоксальности ньютоновского абсолютного времени, которое “по самой своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно, и иначе называется длительностью”. /Ньютон/. Во-первых, пишет Ахундов, само рассмотрение течения времени уже есть представление времени как процесса во времени, а во-вторых, “трудно принять утверждение о равномерном течении времени, ибо это предполагает нечто, контролирующее скорость потока времени. Если же время рассматривается "без всякого отношения к чему-либо внешнему", то какой смысл может иметь предположение, что оно течет неравномерно?” /Ахундов, 1973, с. 338/. При этом М.Д. Ахундов опирается на аналогичные рассуждения Уитроу /Уитроу, 1964, с. 48/.
Можно предположить, что подобного рода соображения препятствуют исследованиям этого таинственного свойства равномерности и выяснению его объективных и субъективных основ. Поэтому равномерность общеизвестного измеряемого общепринятыми единицами физического времени до сих пор либо аксиоматически вводится (в порядке определения или даже просто пояснения понятия времени), либо негласно предполагается как само собой разумеющееся свойство времени.