Трюизмом звучит тезис о том, что решить загадку жизни - это познать жизнь как особую форму движения материи. Однако в этом тезисе заключен глубокий смысл, связанный с тем, что ни в одной области материальной действительности движение - непрерывные изменения состава, структуры и состояний объектов - не имеет столь важного значения, как в живой материи. Можно c полным правом утверждать, что сущность жизни - в ее непрерывном движении. Поэтому раскрыть сущность жизни - это значит раскрыть временную структуру биологических процессов, познать законы временной организации процессов функционирования и развития живых организмов и, в конечном итоге, научиться математически описывать жизнь как особое движение материи.
Серьезным препятствием на пути решения этой задачи является преобладание в живой материи стохастических процессов, требующих для своего описания статистических и вероятностных методов, тогда как в современной науке имеются многочисленные факты, свидетельствующие о том, что развитие организмов, а следовательно, и обеспечивающие это развитие биологические процессы, подчиняются каким-то неизвестным науке динамическим законам, которые скрыты за внешней стохастичностью процессов.
В этом отношении большой интерес представляют работы тех биологов, которые хронометрируют исследуемые процессы не в астрономических единицах физического времени, а в особых единицах длительности, отмеряемых при помощи тех или иных процессов самого изучаемого живого организма. При таком способе хронометрирования обнаруживается удивительное единообразие в развитии организмов, говорящее о существовании внутренних динамических законов развития, которые не могут быть выявлены при использовании общепринятых единиц измерения времени.
Подобный способ временного описания не укладывается в рамки общепринятых представлений о времени. Поэтому даже сами биологи, использующие специфические единицы длительности, склонны рассматривать их не как единицы особого биологического времени, а как некоторые искусственно введенные безразмерные характеристики развития изучаемого живого организма.
Но выше было показано, что равномерность - это не абсолютное свойство одного единственного класса материальных процессов, а соотносительное, и что возможно существование неограниченного множества классов соравномерных процессов. В общем случае различные классы соравномерных процессов взаимно стохастичны. Поэтому можно предположить, что стохастичность биологических процессов в значительной степени обусловлена тем, что материальные процессы биологических систем, объективно структурированные в равномерном биологическом времени, мы хронометрируем и пытаемся теоретически описывать в физическом времени, единицы которого стохастичны по отношению к единицам биологического времени.
Вполне понятно, что признание объективного существования биологического времени будет иметь для естествознания весьма серьезные и далеко идущие последствия и потребует пересмотра многих общепринятых представлений, поскольку при этом исчезнут все те мировые константы и единицы производных величин, в размерностях которых фигурирует размерность времени “секунда”, и возникнут новые константы и единицы производных величин, в размерностях которых будет присутствовать размерность биологического времени; перестанут действовать многие общеизвестные законы физики, в формулировках которых присутствует независимая переменная І tІ , т.е. физическое время, и появятся новые законы, в которых в качестве независимой переменной І t І будет фигурировать биологическое время.
Подобная смена парадигмы требует самого тщательного методологического анализа всего круга проблем, связанных с введением в понятийный аппарат биологии понятия биологическое время. Вполне естественно, что методологический анализ невозможен без определенного вторжения философии в пределы естествознания, но, в отличие от так называемого натурфилософского подхода, он не предполагает получения “готовых решений естественнонаучных проблем путем дедукции этих решений из философских принципов” /Бранский, 1989, с. 28/. Поэтому высказанные в настоящей главе соображения о наиболее фундаментальных единицах биологического времени следует воспринимать лишь как гипотезы, призванные помочь обосновать принципиальную возможность существования наиболее фундаментальных и единых для всех периодов развития живого организма “ квантов” биологического времени.
* * *
Живая материя отличается крайней противоречивостью, которая проявляется в виде удивительного сочетания в ней, во-первых, “поразительной устойчивости” с “тончайшей чувствительностью к изменениям” /Уотермен, 1968, с. 12/ и, во-вторых, невероятного многообразия живых организмов с однотипностью их строения и единством исходных принципов организации и функционирования.
В силу высокой чувствительности биологических систем к изменениям, при попытках математически описать биологические процессы приходится учитывать огромное число в большинстве своем случайно изменяющихся переменных72, что вполне естественно приводит к использованию статистических и вероятностных методов описания. Зависимость биологических процессов от большого числа случайным образом изменяющихся переменных в сочетании с безграничным разнообразием форм жизни наводит некоторых исследователей на мысль о том, что в биологии, в отличие от физики, нет "абсолютных явлений"73.
Но вместе с тем, как показали открытия середины XX столетия в генетике, в биохимии и молекулярной биологии, в анатомии и физиологии клетки, живые организмы, начиная с микроорганизмов и кончая человеком, имеют в своей основе гораздо больше общего, чем можно было предполагать. Так, выяснилось, что они пользуются одним и тем же генетическим кодом для передачи наследственной информации74, всеобщими оказались основные реакции клеточного обмена75, а также многие внутриклеточные структуры76. Подобного рода факты приводят к выводу, что наблюдаемое многообразие форм жизни является в значительной мере внешним и что в основу фантастического многообразия организмов Природой положено поразительно мало принципов /Грин, Голдбергер, 1968, с. 15/. Выявление этих принципов и построение на их основе теоретической биологии, способной количественно описывать как отдельные биологические процессы, так и поведение биологических систем в целом, признавались как наиболее актуальные проблемы науки77. Многим исследователям казалось, что биология наконец-то приближается к построению такой теоретической дисциплины, которая по своим возможностям будет близка к теоретической физике78.
В это время благодаря развитию молекулярной биологии все более глубоко раскрывается фундаментальное значение клетки как основной структурной и функциональной единицы живых организмов и все более широкое признание получает представление о том, что решение многих общебиологических проблем может быть достигнуто лишь "на уровне клетки"79. Поэтому представлялось, что одним из важных этапов в создании теоретической биологии должно явиться построение математической модели клетки и внутриклеточных процессов.
Однако несмотря на огромные успехи ряда наук, занятых изучением клетки80, теоретическая цитология была еще весьма далека от того, чтобы описывать клетку как “... материальное выражение некоего комплекса принципов механики, обладающее уникальной молекулярной архитектурой и организацией” /Грин, Гольдбергер, 1968, с.17/. Анализ же имевшихся в то время попыток создать математическую модель клетки и внутриклеточных процессов приводил исследователей к неутешительному выводу, что “нет сколько-нибудь реальной возможности создания математической модели клетки” /Молчанов, 1967, с.308/.
При рассмотрении причин, затруднявших математическое описание биологических систем, высказывалась даже мысль о том, что “объекты, изучаемые в биологии, чрезвычайно сложны, и сколько-нибудь адекватное их описание лежит, как правило, за пределами возможностей современной математики” /Гнеденко, Фомин, Хургин, 1962, с.103/, формировавшейся на основе количественного описания объектов и процессов неживой природы, и что к адекватному математическому описанию биологических систем и процессов можно будет приблизиться лишь тогда, когда будет разработан математический аппарат, соответствующий природе живой материи81. Разумеется, успешное развитие теоретической биологии может привести к дальнейшему развитию самой математики, однако трудно согласиться с тем, что имевшийся в 60-х годах математический аппарат был недостаточно сложен (или универсален) и поэтому не пригоден для адекватного описания биологических систем и процессов. Неудачи математического описания таких биологических систем, как живая клетка, на наш взгляд, были обусловлены прежде всего неудовлетворительностью понятийного аппарата самой биологии, который в значительной мере состоял из понятий, механически перенесенных в биологию из наук о неживой природе и не отражавших специфики живой материи82. Правы были те авторы, которые, говоря о необходимости развития теории клетки и внутриклеточных процессов, прежде всего подчеркивали важность теоретического обобщения достижений современной биологии. Наиболее четко эта мысль была выражена авторами монографии “Регуляторные механизмы клетки”, которые писали: “За последние два-три десятилетия биология накопила огромный фактический материал описательного характера. В то же время теоретическая биология, теоретические обобщения далеко не соответствуют возможностям, которые создаются благодаря наличию большого объема эмпирических знаний. Хотя проблемами биологии глубоко заинтересовались математики, кибернетики, физики и химики, их стремления в значительной мере сдерживаются тем, что современная теоретическая биология еще не обобщила, не систематизировала накопленный материал с определенной объединяющей позиции и не вскрыла наиболее общие черты строения всего живого, течения процессов жизнедеятельности, не подготовила почвы для моделирования сущности жизни” /Сытник, Кордюм, Кок, 1969, с.3/.
В работах, посвященных изучению и описанию клетки и внутриклеточных связей и процессов, достаточно четко выделились два направления, одно из которых можно назвать структурно-функциональным, другое - феноменологическим.
Первое связано с детальным исследованием структуры клетки и внутриклеточных образований, конкретных физико-химических механизмов взаимодействия различных элементов внутриклеточной организации, каналов внутриклеточной коммуникации, физико-химических свойств материальных носителей информации, способов обмена информацией между отдельными элементами клеточной структуры и т.д.
Разрабатывая это уже достаточно развитое к концу 60-х годов направление исследования, обычно предполагали, что, детально изучив отдельные компоненты клетки, выяснив и исследовав конкретные физико-химические механизмы внутриклеточных связей, можно будет в дальнейшем прийти к синтезу целого в виде некоторой идеальной модели "минимальной клетки". Предполагалось, что эта модель, обладая лишь минимумом необходимого для любой клетки оснащения, будет копировать с той или иной степенью точности (в зависимости от того, что признается "необходимым оснащением") материальную структуру клетки и отдельных ее элементов и позволит, наконец, понять функционирование живой клетки как целостной системы.83
Признавая большую познавательную ценность структурно-функционального направления в изучении живой клетки, мы тем не менее считаем, что при построении математической теории клетки и внутриклеточных процессов значительно более перспективным являлось второе - феноменологическое - направление, связанное с формированием таких теорий, которые, отвлекаясь от причинного анализа внутренних механизмов, управляющих явлениями, сосредоточивают свое внимание на установлении количественных соотношений и описании внешних сторон изучаемых объектов и процессов и дают такую формулировку закономерностей в области наблюдаемых явлений, “в которой не делается попытки свести описываемые связи к лежащим в их основе общим законам природы, через которые они могли бы быть понятыми” /Гейзенберг, 1967, с.731/.
В развитии физики, отмечает В. Гейзенберг, феноменологические теории всегда играли значительную роль, причем они “развиваются всегда там, где наблюдаемые явления еще не могут быть сведены к общим законам природы. Причина этой невозможности может состоять либо в чрезвычайной сложности соответствующих явлений, которая еще не допускает такое сведение из-за математических трудностей, либо в незнании упомянутых законов” /Там же/. Еще более важная причина частого обращения в физике к феноменологическим теориям заключается в том, что материальными носителями действующих в неживой природу "сил", а также материальными субстратами эмпирически наблюдаемых явлений и процессов оказываются объекты и процессы микромира, труднодоступные для экспериментального изучения. Поэтому общие законы природы, которые лежат в основе объяснения многих явлений физического мира, нередко сами оказываются феноменологическими теориями более фундаментальных процессов и явлений неживой природы.
Совершенно иначе обстоит дело в биологии. Здесь "материальные механизмы" процессов жизнедеятельности живого организма оказались "слишком доступными" для непосредственного наблюдения. Более того, доступными для непосредственного экспериментального изучения оказались материальные носители не только собственно биологических, но и многих лежащих в их основе физических и химических процессов. Отсюда велик соблазн искать "механизмы" биологических процессов в области химических реакций и физических взаимодействий на уровне молекул, атомов и даже элементарных частиц, "из которых состоят биологические системы" и которые "лежат в основе биологических процессов". Поэтому сложность построения в биологии таких феноменологических теорий, которые адекватно отражали бы специфику живой материи, заключается в трудности абстрагирования от доступных непосредственному наблюдению молекулярных "механизмов" наиболее фундаментальных биологических процессов, а следовательно, и от тех физических и физико-химических теорий, которые позволяют математически описывать функционирование этих "механизмов". Ситуация усугубляется еще и тем, что господствующая в экспериментальной биологии редукционистская установка не позволяет уделять должное внимание поискам собственно биологических, не подчиняющихся физическим и физико-химическим законам принципов организации биологических процессов84. Более того, на наш взгляд, именно редукционистский способ мышления помешал исследователям, занятым проблемами теоретического описания биологических процессов, должным образом оценить выдающееся по своей сути эмпирическое открытие рядом биологов биологического времени.
Правильному восприятию результатов исследований таких ученых, как Х. Фрай, Г. Кейт, К. Торнтвейт, Г.П. Еремеев, Д.А. Сабинин, Т.А. Детлаф и др., мешало и то обстоятельство, что признание используемых ими единиц длительности единицами особой формы времени вступало в резкое противоречие с общепринятыми представлениями, согласно которым время - это нечто единое, универсальное, всеобщее, равномерно текущее и достаточно точно измеряемое общепринятыми единицами при помощи обычных часов. Вполне естественно, что, не имея достаточно обоснованного положительного решения философской проблемы многообразия форм времени, трудно отойти от господствующих в сознании людей понятий и признать биологическое время столь же полноценным, каким признается физическое время.
Но, как мы показали, принятые ныне представления о времени нуждаются в серьезном пересмотре. Мнение об уникальности времени и о принципиальной невозможности его измерения не иначе, как обычными часами и общепринятыми единицами, основано на негласном признании единственности класса равномерных и строго периодических процессов. Анализ же свойств равномерности и периодичности материальных процессов показал, что они являются не абсолютными, а соотносительными свойствами и что в принципе возможно существование неограниченного множества соравномерных (и периодических эквивалентных) процессов.
В предыдущей главе был рассмотрен класс инерциально-равномерных движений, от которых абстрагировано общепринятое представление о времени, и было показано, что соравномерность входящих в этот класс механических движений возникает благодаря подчиненности соответствующих динамических систем закону сохранения механической энергии. Но соравномерность материальных процессов может быть обусловлена и другими причинами, например, принадлежностью их целостной высокоинтегрированной материальной системе. Примерами таких систем являются живые организмы.
О том, что в живых организмах существуют классы соравномерных процессов, синхронно и пропорционально ускоряющих и замедляющих свой ход под воздействием множества различных и, в том числе, случайным образом изменяющихся факторов, свидетельствуют результаты исследований Т.А. Детлаф и ее коллег. Они установили, что с изменением температуры среды длительности различных этапов эмбрионального развития пойкилотермных животных изменяются пропорционально и что эта закономерность имеет фундаментальный характер, охватывая процессы всех структурных уровней организации эмбриона. Как пишет Т.А. Детлаф, “... с изменением температуры пропорционально изменяется длительность процессов, имеющих самую разную природу и осуществляющихся на разных уровнях организации организма: внутриклеточном (молекулярном и ультраструктурном), клеточном (при делении клеток и их дифференцировке), на уровне морфогенетических движений, процессов индукции и органогенеза” /Детлаф, 1996, с. 140/. Иными словами, вся совокупность биологических процессов, из которых складывается развитие эмбриона, ведет себя как единый целостный поток, синхронно и пропорционально изменяя свою скорость в зависимости от изменений температуры среды. В этом едином потоке имеются как сравнительно медленные (например, протекающие на клеточном уровне процессы деления клеток и их дифференцировка), так и весьма быстрые, протекающие на внутриклеточном, молекулярном уровне, к которым относятся, например, ферментативные реакции внутриклеточного метаболизма. При этом достаточно очевидно, что если бы на каких-то структурных уровнях организации эмбриона нарушалась синхронность и пропорциональность изменения темпов биологических процессов, то это разрушило бы закономерное течение всего потока процессов формирования и развития живого организма. Подчеркивая это обстоятельство, Т.А. Детлаф пишет: “Не будет преувеличением, если мы скажем, что без этой способности пойкилотермные организмы вообще не могли бы существовать в меняющихся условиях внешней среды: если бы разные компоненты комплекса процессов, из которых складывается любой этап развития, изменялись асинхронно, то это приводило бы к возникновению нарушений нормального развития, а на более поздних стадиях - к нарушению нормального функционирования организма. Не случайно, что одной из первых реакций зародышей на приближение к границам оптимальных температур является десинхронизация отдельных процессов развития”85 /Там же/.
Пропорциональность изменений длительностей различных процессов эмбрионального развития пойкилотермных животных при изменениях температуры внешней среды позволяет, взяв за единицу длительность одного из этапов эмбрионального развития, выразить через нее длительности всех остальных этапов. В качестве такой единицы в лаборатории Т.А. Детлаф избрана длительность одного митотического цикла периода синхронных делений дробления (t ![]() ), получившей наименование “ детлаф” . Для того, чтобы длительности разных этапов эмбрионального развития, измеряемые на практике в минутах, перевести в “ детлафы” , предварительно для каждого вида исследуемых животных во всем диапазоне оптимальных температур определяются (в минутах) величины t
), получившей наименование “ детлаф” . Для того, чтобы длительности разных этапов эмбрионального развития, измеряемые на практике в минутах, перевести в “ детлафы” , предварительно для каждого вида исследуемых животных во всем диапазоне оптимальных температур определяются (в минутах) величины t ![]() и строятся графики зависимости t
и строятся графики зависимости t ![]() от температуры86. Непосредственно хронометрируя развитие эмбрионов в минутах, длительности этапов развития переводятся в “ детлафы” простым делением полученных величин на величину t
от температуры86. Непосредственно хронометрируя развитие эмбрионов в минутах, длительности этапов развития переводятся в “ детлафы” простым делением полученных величин на величину t ![]() , соответствующую температуре среды, при которой идет развитие эмбриона.
, соответствующую температуре среды, при которой идет развитие эмбриона.
Такой способ перевода минут в “ детлафы” может создать ложное представление о том, что измеряемое при помощи детлафов биологическое время - это аффинно преобразованное физическое время87. В действительности же биологическое время взаимно стохастично с физическим и не может быть результатом аффинного преобразования физического времени. Но для того, чтобы выявить взаимную стохастичность биологического и физического времени, необходимо от измеряемой детлафами макроструктуры биологического времени перейти к измеряемой значительно более мелкими единицами его “ тонкой структуре” . Возможность перехода от детлафов к более мелким единицам измерения длительности обеспечена тем, что синхронность и пропорциональность изменений длительностей биологических процессов представляют собой фундаментальное свойство живой материи и охватывают процессы всех уровней ее организации. Поэтому если в некотором интервале длительности содержится Р![]() периодов биологических процессов одного уровня и Р
периодов биологических процессов одного уровня и Р![]() периодов другого уровня, то отношение Р
периодов другого уровня, то отношение Р![]() / Р
/ Р![]() будет оставаться константой при любых (допустимых) изменениях температуры. Обозначив величину этого отношения через С, мы имеем: Р
будет оставаться константой при любых (допустимых) изменениях температуры. Обозначив величину этого отношения через С, мы имеем: Р![]() = С* Р
= С* Р![]() . Таким образом, если в некотором интервале укладывается одна крупная единица, то в этом интервале уложится С мелких единиц. Иными словами, константа С представляет собой масштабный коэффициент при переходе от единиц биологического времени более высокого “ макроскопического” ) уровня к единицам более низкого (“ микроскопического” ) уровня.
. Таким образом, если в некотором интервале укладывается одна крупная единица, то в этом интервале уложится С мелких единиц. Иными словами, константа С представляет собой масштабный коэффициент при переходе от единиц биологического времени более высокого “ макроскопического” ) уровня к единицам более низкого (“ микроскопического” ) уровня.
При переходе от одного масштаба биологического времени к другому мы увидим , что если на уровне медленных, измеряемых “ детлафами” процессов температуру среды можно рассматривать как изменяющуюся медленно и плавно, а на протяжении отдельных этапов эмбрионального развития считать и вовсе постоянной, то на уровне быстрых внутриклеточных процессов мы не можем игнорировать быстрые стохастические колебания температуры. Поэтому определяемые быстрыми внутриклеточными процессами мелкие единицы биологического времени обретают характер стохастической переменной величины по отношению к равномерному физическому времени. Иными словами, в своей “ тонкой структуре” биологическое время оказывается взаимно стохастичным с физическим временем, а следовательно, при достаточно точном измерении оно стохастично с физическим временем и на более высоких уровнях. Но если коэффициент С достаточно велик и, следовательно, крупные единицы биологического времени состоят из большого числа мелких единиц, то случайные колебания последних, усредняясь, весьма слабо скажутся на величинах крупных единиц.
Взаимная стохастичность биологического и физического времени на уровне их “ тонкой структуры” говорит о том, что при хронометрировании протекающих в живом организме материальных процессов в единицах биологического времени единицы физического времени становятся последовательностью случайных величин. Но справедливо и обратное: если хронометрировать биологические процессы в единицах физического времени, то все процессы, которые в биологическом времени подчиняются динамическим законам, предстанут как стохастические процессы88.
Вполне естественно предположить, что при таком характере взаимосвязи биологического и физического времени биологические процессы в живом организме начинаются только с определенного уровня организации его материального субстрата и, соответственно, на этом уровне возникает биологическое время. Имеются определенные основания считать, что таким фундаментальным уровнем структурной организации живой материи и протекающих в ней биологических процессов является уровень ферментативных реакций внутриклеточного метаболизма.
Приступая к обсуждению этого вопроса, мы прежде всего должны отметить, что во временной структуре внутриклеточных процессов ферментативные реакции метаболизма относятся к наиболее быстрым процессам. На это обстоятельство обратил свое внимание в 60-х годах Б. Гудвин в весьма интересной, с точки зрения обсуждаемой нами проблемы, книге “Временная организация клетки” /Гудвин, 1966/.
Опираясь на разработанную в современной физике идею разделения нестационарных процессов на качественно различные ступени, относящиеся в соответствии с их временами релаксации к разным масштабам времени89, Б. Гудвин, вслед за Уоддингтоном, делит внутриклеточные процессы на следующие три группы: 1/ Быстрые биохимические процессы, включающие транспорт и химические превращения "малых" молекул ("метаболическая система"); 2/ обладающие средними скоростями процессы биосинтеза, диффузии и взаимодействия макромолекул ("эпигенетическая система") и 3/ совокупность медленных генетических изменений биологических систем ("генетическая система").
В своей работе Б. Гудвин отвлекается как от слишком медленных генетических изменений параметров клетки, так и от слишком быстрых процессов метаболической системы и ставит перед собой задачу смоделировать процессы, относящиеся к эпигенетической системе клетки. Исходя из того факта, что времена релаксации процессов метаболической и эпигенетической систем клетки лежат соответственно в пределах ![]() и
и ![]() сек., автор полагает, что частоты колебательных явлений метаболической системы достаточно велики и поэтому лежат вне временного диапазона процессов эпигенетической системы и что при описании последних можно использовать допущение о стационарности метаболической системы. При этом оказалось, что если полностью отвлечься от подверженных случайным колебаниям процессов метаболической системы, то имеющие колебательный характер процессы эпигенетической системы можно описать как совокупность подчиняющихся не статистическим, а динамическим законам биохимических осцилляторов.
сек., автор полагает, что частоты колебательных явлений метаболической системы достаточно велики и поэтому лежат вне временного диапазона процессов эпигенетической системы и что при описании последних можно использовать допущение о стационарности метаболической системы. При этом оказалось, что если полностью отвлечься от подверженных случайным колебаниям процессов метаболической системы, то имеющие колебательный характер процессы эпигенетической системы можно описать как совокупность подчиняющихся не статистическим, а динамическим законам биохимических осцилляторов.
Однако процессы эпигенетической системы невозможно рассматривать как абсолютно не зависящие от биохимических реакций метаболической системы и поэтому их приходится рассматривать "погруженными" в "шумящее", т.е. подверженное случайным колебаниям, "биохимическое пространство" метаболической системы клетки. Но поскольку это "пространство" не определено однозначно, то, как пишет автор, “траектории детерминированных осцилляторов ("эпигенетической системы". - И.Х) перестают быть строго детерминированными. Поэтому приходится говорить только об усредненных траекториях, и все динамические свойства управляющих систем (клетки. - И.Х.) должны описываться с вероятностных позиций” /Гудвин, 1966, с.100-101/.
Таким образом, в результате воздействия на осцилляторы эпигенетической системы случайных колебаний процессов метаболической системы эпигенетическая система оказывается набором стохастических осцилляторов, а поскольку входящие в эпигенетическую систему процессы биосинтеза, диффузии и взаимодействия макромолекул лежат в основе регуляторных механизмов клетки, то и вся клетка предстает как совокупность почти не связанных между собой и подчиняющихся вероятностным законам биохимических осцилляторов. Однако подобное уподобление клетки газу не отражает природы живой материи, и мы вполне согласны с А.М. Молчановым, который, отмечая, что при математическом описании клетки пока приходится выбирать между двумя крайними подходами, из которых один уподобляет клетку механизму, другой - газу, писал: “ При всей грубости и жесткости первого подхода он неизмеримо ближе к истине, чем второй, так как исходит из главного - высокой степени эволюционной зрелости такого замечательного и сложно организованного биологического объекта, как клетка” /Молчанов, 1967, с.308/.
Одной из наиболее важных причин неудачи Б. Гудвина в моделировании временной структуры внутриклеточных процессов, на наш взгляд, явилось игнорирование им быстрых биохимических реакций внутриклеточного метаболизма. Он полагал, что при математическом описании клетки можно усреднять параметры, зависящие от наиболее быстрых метаболических процессов, и в основу математической модели клетки можно положить уравнения, описывающие сравнительно медленные процессы эпигенетической системы. Подобный путь к описанию клетки представляет собой своего рода "макроскопический" (во временном отношении) подход к биологическим процессам. При этом он исходил из предположения, что “...для адекватного описания феноменологических свойств макроскопической системы вовсе не обязательно использовать микроскопический подход” /Гудвин, 1966, с.101/. Однако он упустил из виду, что при макроскопическом подходе к описанию материальных систем и процессов легко могут ускользнуть из поля зрения нарушающие какую-либо важную симметрию мира и тем самым качественно изменяющие реальную действительность бесконечно малые (с точки зрения макроскопического уровня) возмущения описываемой системы90.
Именно с такого рода ситуацией мы и сталкиваемся при попытках усреднять параметры метаболической системы клетки и описывать протекающие в клетке процессы в единицах физического времени. При этом нарушается самоконгруэнтность единиц биологического времени и стохастичность единиц физического времени относительно биологического оборачивается стохастичностью биологических процессов относительно физического времени.
О недопустимости отношения к метаболическим процессам как к некоторому "биохимическому фону", на котором разыгрываются сравнительно медленные "собственно биологические" процессы эпигенетической системы, говорят и многочисленные факты, свидетельствующие о том, что относящиеся к метаболической системе клетки ферментативные реакции внутриклеточного обмена веществ составляют содержание, "живую ткань" собственно биологических процессов.
В пользу предположения о том, что наиболее фундаментальные единицы биологического времени следует искать среди периодов циклических метаболических процессов клетки, можно привести и следующий аргумент.
Рассмотренные нами работы биологов, использующих специфические единицы измерения длительности, и в особенности работы Т.А. Детлаф и ее коллег, на наш взгляд, убедительно доказывают, что биологические процессы живых организмов объективно структурированы в особом биологическом времени. Но тогда логично предположить, что временные характеристики генетической информации также должны быть закодированы в единицах биологического времени. Для того чтобы это могло быть выполнено, во-первых, должны существовать естественные единицы (“ кванты” ) времени и, во-вторых, они должны быть связаны с такими процессами, которые позволяют вести непрерывный их счет с момента оплодотворения яйцеклетки и до гибели живого организма. Такими “ сквозными” для всех этапов развития организма биологическими процессами, видимо, являются лишь ферментативные реакции внутриклеточного метаболизма.
Центральными двигателями метаболического процесса, своеобразными “ машинами метаболизма” являются молекулы фермента, представляющие собой гигантские макромолекулы, имеющие весьма сложную структуру.
На протяжении длительного времени предполагалось, что конформационные изменения макромолекул белка представляют собой результат каких-либо определенных воздействий на фермент извне (например, слабого нагревания, взаимодействия с теми или иными метаболитами, ионами металлов и т.д. (См., например: /Кретович,1967/). Но открытые в конце 50-х годов С.Э. Шнолем /Шноль, 1958/ и затем подробно изученные им и его сотрудниками самопроизвольные циклические изменения многих показателей растворов актина, миозина и актомиозина свидетельствуют о том, что белковая молекула по самой своей природе является динамичной, постоянно и самопроизвольно изменяющей свою пространственную структуру системой91. В дальнейшем на основе значительных серий опытов с большим числом различных препаратов было показано, что самопроизвольные конформационные колебания являются свойством всех белков /Шноль и др., 1980/.
Для объяснения механизмов ферментативного катализа большой интерес представляют, на наш взгляд, высказываемые некоторыми авторами мысли о том, что молекула фермента участвует в катализируемой ею реакции “не только как штатив, закрепляющий детали механизма, но и как двигатель в этом механизме”92 /Шноль, 1967, с. 27/.
Мнение о том, что молекула фермента представляет собой своего рода "энергетическую машину" /Робертис и др., 1967, с.59/, которая при наличии некоторого источника энергии способна совершать определенную работу по перестройке химической структуры молекул субстрата катализируемой ею реакции, по нашему мнению, более адекватно отражает природу биологических катализаторов, чем отождествление их с обычными химическими катализаторами.
В настоящее время можно считать доказанным, что каждый элементарный акт ферментативного катализа представляет собой многоступенчатый циклический процесс, в ходе которого молекула фермента соединяется с молекулой (или молекулами) субстрата и образуется так называемый фермент-субстратный комплекс, который, претерпев ряд последовательных изменений, распадается на свободный фермент и конечный продукт (или продукты) реакции93, и может начаться новый цикл каталитического процесса.
Поскольку при этом предполагается, что в макроскопическом объеме реагирующей среды единичные акты ферментативного катализа распределены в пространстве и во времени случайным образом, то усреднение во времени протекающих в реагирующей среде химических превращений позволяет отдельные стадии ферментативного катализа рассматривать как самостоятельные химические реакции, связанные между собой через участвующие в каталитическом процессе реагенты и промежуточные соединения.
В основе теории химических реакций лежит введенное Эйрингом /Eyring, 1935/ представление о том, что, прежде чем претерпеть химическое изменение, молекулы субстрата проходят через переходное, так называемое, активированное состояние с максимальной энергией. Поскольку время жизни субстратов и продуктов реакции много больше времени существования активированного комплекса, то каждый элементарный акт химической реакции рассматривается как мгновенное событие. При этом предполагается, что в макроскопических объемах реагирующей среды, где совершается большое число элементарных химических превращений, происходит усреднение во времени мгновенных "скачков", и химическая реакция может рассматриваться как непрерывный процесс.
Аналогичные представления о непрерывности протекающих в макроскопических объемах реагирующей среды химических превращений используются и в теории ферментативного катализа. Однако еще в начале 60-х годов серьезные возражения против подобных представлений высказал Христиансен /Christiansen, 1960/.
Предположим, пишет Христиансен, реакция
В![]() + В
+ В![]() + В
+ В![]() = А
= А![]() + А
+ А![]() + А
+ А![]() , / В /
, / В /
имеющая положительное направление слева направо, катализируется ферментом в три ступени
В![]() + Х
+ Х![]() = Х
= Х![]() + А
+ А![]() / 1 /
/ 1 /
В![]() + Х
+ Х![]() = Х
= Х![]() + А
+ А![]() / 2 / / А /
/ 2 / / А /
В![]() + Х
+ Х![]() = Х
= Х![]() + А
+ А![]() , / 3 /
, / 3 /
где ![]() - три различные формы фермента или фермент-субстратного комплекса.
- три различные формы фермента или фермент-субстратного комплекса.
Формула ![]() означает, что реакция
означает, что реакция ![]() заставляет фермент пройти циклические изменения в порядке 1231, что должно наблюдаться как появление и исчезновение одного из продуктов или субстратов.
заставляет фермент пройти циклические изменения в порядке 1231, что должно наблюдаться как появление и исчезновение одного из продуктов или субстратов.
Предположим далее, что мы наблюдаем реакцию в момент, когда ![]() превращается в
превращается в ![]() , что, согласно рассмотренным выше представлениям, является скачкообразным, пока мы рассматриваем только одну молекулу фермента. Иными словами, в силу малости времени переходов через обозначенные знаком равенства активированные состояния участвующих в реакции молекул, мы можем считать, что молекула фермента в каждый определенный момент времени может находиться только в одном из трех возможных состояний
, что, согласно рассмотренным выше представлениям, является скачкообразным, пока мы рассматриваем только одну молекулу фермента. Иными словами, в силу малости времени переходов через обозначенные знаком равенства активированные состояния участвующих в реакции молекул, мы можем считать, что молекула фермента в каждый определенный момент времени может находиться только в одном из трех возможных состояний ![]() ,
, ![]() и
и ![]() .
.
Переходя к рассмотрению случая, когда в элементе объема содержится большое число молекул фермента, Христиансен пишет: “Можем ли мы предполагать, что различные молекулы находятся одновременно в одном и том же состоянии? Или, выражаясь иными словами, является ли мгновенное распределение ферментов по различным состояниям одинаковым по всей реагирующей среде?
Согласно термодинамике, ясно, что ответ на поставленный вопрос должен быть утвердительным, поскольку мы знаем, что для того, чтобы перевести всю систему из состояния, в котором распределение по всей системе одинаково, в состояние с разным распределением, требуется затрата работы. Поэтому первое состояние более вероятно, чем второе, и, как обычно в статистической термодинамике, настолько, что практически оно одно и возможно. Мы можем поэтому считать, что циклические трансформации отдельных молекул фермента должны всегда происходить в фазе или что система должна быть когерентна в отношении превращений фермента” /Там же, с.108/.
К выводам, аналогичным тем, к которым пришел Христиансен, можно прийти и в том случае, если качественно проанализировать совокупность физических и физико-химических процессов, составляющих ферментативный каталитический цикл.
Представим себе, что в некотором ограниченном объеме внутриклеточной среды, состоящей в основном из молекул воды и растворенных в ней, как правило, небольших молекул реагентов (субстратов и продуктов), а также некоторых других веществ, протекает катализируемая молекулами фермента биохимическая реакция.
В этой среде резко выделяются гигантские макромолекулы фермента, состоящие из многих сотен атомов и имеющие сложную пространственную структуру. Они представляют собой осцилляторы, в которых колебания происходят как на уровне элементарных частиц и атомных ядер, так и на уровне достаточно крупных групп атомов. Среди огромного числа колебательных систем всегда найдутся осцилляторы, способные воспринять кинетическую энергию соударяющихся с макромолекулой фермента молекул среды, молекулярные веса которых, как правило, сравнимы с молекулярными весами внутримолекулярных осцилляторов. Если при этом учесть, что момент инерции центра массы макромолекулы велик и что соударения молекул среды с молекулой фермента распределены по поверхности последней случайным образом, то можно сделать вывод, что воспринимаемая макромолекулой внутренняя (молекулярно-кинетическая) энергия окружающей среды будет в основном идти на возбуждение ее колебательных систем, а не на возбуждение броуновского движения ее центра масс.
Поскольку между колебательными системами макромолекулы существуют различного типа связи, то воспринятая теми или иными осцилляторами внутренняя энергия окружающей среды будет передаваться вдоль некоторых связей другим осцилляторам, и в молекуле фермента возникнут потоки колебательной энергии. В силу того, что связи, вдоль которых может передаваться колебательная энергия, должны удовлетворять определенным условиям /Мандельштам, 1955/, то при каждой конформации в макромолекуле будут существовать вполне определенные пути миграции колебательной энергии. Миграция колебательной энергии может быть причиной конформационных изменений макромолекулы, поскольку при некоторых распределениях энергии в ней могут временно разрываться (или, по крайней мере, ослабляться) те или иные внутримолекулярные связи, что может нарушать устойчивость конформации, а при некоторых дополнительных условиях, например, при достижении суммарной колебательной энергии определенных критических значений, и к переходу макромолекулы в иную конформацию.
Если учесть, что в общем случае внутримолекулярные связи ограничивают число колебательных степеней свободы внутримолекулярных осцилляторов, то разные конформации макромолекулы фермента, обладая, как правило, разным числом внутримолекулярных связей, характеризуются и разным числом колебательных степеней свободы, а следовательно, разной степенью энергетической емкости. Однако переход от конформации с меньшим числом внутримолекулярных связей к конформации с большим их числом должен сопровождаться уменьшением накопленной в макромолекуле колебательной и конформационной энергии, поэтому такой переход требует для погашения "избыточной" энергии каких-то "точек приложения". Подобной "точкой приложения" может служить перестраиваемая при ферментативной реакции химическая структура молекулы (или молекул) субстрата катализируемой ферментом реакции.
В силу большой частоты соударений молекул среды с макромолекулой фермента, мы можем считать, что преобразуемая в колебательную энергию внутримолекулярных осцилляторов внутренняя энергия окружающей среды "втекает" в макромолекулу в виде непрерывного потока. Но поскольку тепловое движение молекул среды подвержено флуктуациям, то интенсивность потока энергии будет также флуктуирующей величиной. Поэтому длительность пребывания макромолекулы фермента в состоянии устойчивой конформации будет случайной величиной.
Рассматривая среду, в которой протекает катализируемая растворенными в ней молекулами фермента биохимическая реакция, С.Э. Шноль пишет:: “Представим себе... большое число... макромолекул фермента в растворе, содержащем соответствующий субстрат. По существу речь здесь идет о множестве генераторов механических колебаний, распределенных в среде, в которой они совершают циклические изменения конформации. Поскольку эти генераторы полностью идентичны, обязательно должно происходить их взаимодействие, приводящее к образованию упорядоченных в пространстве синхронно колеблющихся ассоциаций ферментных макромолекул. В результате в растворе должны образоваться структуры типа жидких кристаллов, отличающихся от обычных своей эфемерностью - они представляют собой ансамбли лишь работающих макромолекул фермента” /Шноль, 1979, с. 74/.
С.Э. Шноль рассматривает здесь ферментативный процесс в динамике, а мы для уяснения некоторых особенностей этого процесса остановим его и рассмотрим поэтапно.
Представим себе, что макромолекулы фермента, находящиеся в одной из своих устойчивых конформаций, образуют описанную выше кристаллическую структуру. Поскольку каждая молекула фермента состоит из огромного числа в общем случае электрически заряженных и совершающих колебательные движения групп атомов, то вокруг каждой ферментной молекулы должны существовать сложные электростатические и электромагнитные поля. А если учесть, что молекулы воды представляют собой диполи94, определенным образом ориентирующиеся в электростатических полях, возникающих вокруг и между макромолекул фермента, то можно предположить, что на тех этапах каталитического цикла, когда молекулы фермента находятся в своих устойчивых конформациях, жидкокристаллическую структуру обретает и окружающая молекулы фермента водная среда. В такой среде будут существенно нарушены многие действующие в обычной жидкости гидродинамические законы, в частности, предельно снижена скорость диффузии веществ.
Однако картина резко меняется в моменты скачкообразных переходов макромолекул от одной конформации к другой, поскольку при этом резко перестраивается структура электростатических и электромагнитных полей, а часть освобождаемой конформационной энергии рассеивается в окружающую среду, разрушая ее кристаллическую структуру и усиливая тепловое движение молекул среды. Эти короткие "мгновения" конформационных переходов предельно малы по сравнению с длительностью периодов существования устойчивых конформаций. Тем не менее они имеют определенную временную длительность, на протяжении которой восстанавливается "нормальное" действие гидродинамических законов, а скорость диффузии различных веществ в результате интенсивного перемешивания среды значительно возрастает. Но как только макромолекула фермента примет новую устойчивую конформацию и стабилизируются окружающие ее физические поля, реагирующая среда примет новую кристаллическую структуру и снова обретет жидкокристаллические свойства.
Таким образом, имеются определенные основания предположить когерентность каталитических циклов молекул фермента, катализирующих в клетке данную биохимическую реакцию95.
Рассмотрим теперь более подробно временную структуру каталитических циклов.
Обозначим длительность ![]() -го каталитического цикла через
-го каталитического цикла через ![]() , длительность существования
, длительность существования ![]() -ой устойчивой конформации
-ой устойчивой конформации ![]() -го каталитического цикла - через
-го каталитического цикла - через ![]() длительность перехода от
длительность перехода от ![]() -ой устойчивой конформации к
-ой устойчивой конформации к ![]() -ой конформации
-ой конформации ![]() -го каталитического цикла - через
-го каталитического цикла - через ![]() . При этом будем считать, что первой устойчивой конформацией участвующего в каталитическом процессе фермента является свободный фермент, а последним (n-ым) конформационным переходом - переход, при котором выделяется свободный фермент и таким образом начинается новый каталитический цикл.
. При этом будем считать, что первой устойчивой конформацией участвующего в каталитическом процессе фермента является свободный фермент, а последним (n-ым) конформационным переходом - переход, при котором выделяется свободный фермент и таким образом начинается новый каталитический цикл.
При таких обозначениях полную длительность ![]() -го каталитического цикла можно представить как сумму
-го каталитического цикла можно представить как сумму![]()
![]()
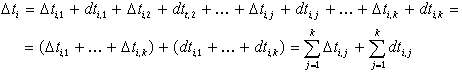
Поскольку второй член много меньше первого и с большой степенью точности во всех каталитических циклах сохраняется постоянным, то полный период каталитического цикла будет зависеть в основном от длительностей существования устойчивых конформаций фермента и фермент-субстратного комплекса, т.е. от величины первого члена этой суммы. Но как мы отметили выше, длительность существования устойчивой конформации фермента зависит от постоянно флуктуирующей интенсивности "втекающего" в макромолекулу фермента потока тепловой энергии окружающей среды. Поэтому длительности существования фермента в данной устойчивой конформации в разных каталитических циклах, т.е. ![]() при переменном
при переменном ![]() и постоянном индексе
и постоянном индексе ![]() , будут случайными величинами. Следовательно, случайными будут и полные периоды последовательных серий каталитических циклов, т.е.
, будут случайными величинами. Следовательно, случайными будут и полные периоды последовательных серий каталитических циклов, т.е. ![]() .
.
Однако каждый каталитический цикл данной ферментативной реакции, независимо от выраженной в единицах физического времени длительности цикла, вносит в реагирующую среду вполне определенные изменения, которые для серии следующих друг за другом каталитических циклов будут оставаться неизменными.
Действительно, каждая участвующая в каталитическом процессе молекула фермента за один каталитический цикл расходует определенное количество молекул субстрата, производит определенное количество молекул продукта катализируемой реакции, а также расходует или выделяет (в зависимости от энергетических характеристик реакции) определенное количество энергии. При этом каталитические циклы состоят из одинаковых последовательностей конформационных переходов ферментных молекул, в ходе которых реагирующая среда претерпевает вполне определенную последовательность как циклических, так и однонаправленных необратимых изменений. Так, на протяжении каждого каталитического цикла в определенной последовательности появляются и исчезают различные конформации фермента и фермент-субстратного комплекса; резко меняются свойства реагирующей среды в периоды скачкообразных переходов макромолекул фермента от одной устойчивой конформации к другой; причем независимо от того, идет ли реакция в целом с поглощением или выделением энергии, при конформационных переходах некоторая часть энергии молекулы фермента рассеивается в реагирующую среду и расходуется на разрушение ее кристаллической структуры. И, наконец, резкие изменения пространственной конфигурации макромолекулы должно вести к резким скачкам амплитуд электромагнитных излучений его электрически заряженных осцилляторов.
Общая длительность каталитического цикла зависит в основном от продолжительности существования стабильных конформаций (т.е. от величин, когда реагирующая среда находится в жидкокристаллическом состоянии и все ее изменения сведены до минимума. Изменения реагирующей среды возникают в моменты конформационных переходов макромолекул фермента, т.е. на протяжении интервалов ![]() , величины которых зависят только от физических и физико-химических характеристик смежных конформаций, в силу чего отличаются высокой степенью постоянства. Поэтому реагирующая среда на протяжении каждого каталитического цикла претерпевает “ дозированные” изменения, определяемые диффузией различных веществ, результатами самой реакции, а также других процессов, протекающих на протяжении последовательных интервалов
, величины которых зависят только от физических и физико-химических характеристик смежных конформаций, в силу чего отличаются высокой степенью постоянства. Поэтому реагирующая среда на протяжении каждого каталитического цикла претерпевает “ дозированные” изменения, определяемые диффузией различных веществ, результатами самой реакции, а также других процессов, протекающих на протяжении последовательных интервалов ![]() в жидкой фазе реагирующей среды. Таким образом, случайные колебания величин
в жидкой фазе реагирующей среды. Таким образом, случайные колебания величин ![]() не влияют на биологически значимые результаты каталитического цикла: для количественной характеристики биологически значимых результатов ферментативного процесса важно количество циклов, а не измеренные в единицах физического времени их длительности.
не влияют на биологически значимые результаты каталитического цикла: для количественной характеристики биологически значимых результатов ферментативного процесса важно количество циклов, а не измеренные в единицах физического времени их длительности.
Что касается количества участвующих в реагирующей среде макромолекул фермента, то оно не подвержено случайным колебаниям, а целенаправленно регулируется при помощи различных модификаторов (активаторов и ингибиторов) и поэтому может быть представлено как функция некоторых параметров.
На основе изложенного можно предположить, что биологически значимая длительность бытия живой клетки определяется не количеством единиц физического времени, а количеством каталитических циклов каких-то ведущих ферментативных реакций внутриклеточного метаболизма или, возможно, более сложных многоступенчатых циклических ферментативных процессов (типа цикла Кребса).
Следует особо заметить, что в интервалах длительности, меньших, чем полные периоды каталитических циклов, в реагирующей среде еще нет биологических процессов, а протекают физические и физико-химические процессы, которые, благодаря специфической организации реагирующей среды и специфическим свойствам молекул фермента, на протяжении каталитического цикла интегрируются в элементарные акты биохимической реакции и связанных с ними биофизических и физиологических процессов. Вместе с тем было бы ошибочным предполагать, что математически развитую теорию элементарных актов биологических процессов можно будет построить на основе физических и физико-химических теорий тех процессов, из которых состоит каталитический цикл ферментативной реакции, поскольку для этого, во-первых, пришлось бы объединять в единую синтетическую теорию качественно разные физические теории, описывающие поведение реагирующей среды в жидком и жидкокристаллическом состояниях, и, во-вторых, учесть стохастичность величин ![]() .
.
Таким образом, биологическое время представляет собой не континуальное, а дискретное квантованное время, неделимыми квантами которого являются полные периоды каталитических циклов каких-то ведущих ферментативных реакций внутриклеточного метаболизма.
Квантованность биологического времени обусловлена, на наш взгляд, и тем обстоятельством, что реализация генетической информации требует достаточно жесткого контроля со стороны генетического аппарата клетки за временными характеристиками процессов становления и развития живого организма. Если при этом допустить, что в генетическом аппарате клетки ведется счет квантам биологического времени, то каждая клетка многоклеточного живого организма, ведя свое происхождение от одной единственной яйцеклетки, “может знать” на каждый данный момент времени количество прожитых организмом “квантов” биологического времени и с учетом этого реализовывать дальнейшие фрагменты генетической информации. Правда, для подобной согласованности во времени деятельности генетических аппаратов всех клеток живого организма необходима синхронизация во всех клетках каталитических циклов ферментативных реакций, которые задают кванты биологического времени, что, на первый взгляд, представляется совершенно невероятным. Но такое предположение оказывается вполне допустимым, если учесть открытое С.Э. Шнолем и на протяжении нескольких десятилетий изучаемые им и его коллегами явление синхронизации макроскопических флуктуаций колебательных процессов различной природы96.
В 1956 г. С.Э. Шноль, работая с препаратами мышечных белков, обратил внимание на необычно большой разброс результатов измерений АТФ-азной активности фермента миозина. Изучение всевозможных источников ошибок: недостаточности перемешивания, негомогенности растворов, непостоянства температуры, нестабильности измерительных приборов и т.д., - привело С.Э. Шноля к выводу, что причиной наблюдаемого разброса измеряемых величин является колебательный характер протекающих в растворах белка процессов. Это заставило С.Э. Шноля и других исследователей, заинтересовавшихся этим явлением, обратиться к исследованию колебательных процессов в биохимических системах. Первые результаты были обсуждены на 1 Всесоюзном симпозиуме по колебательным процессам в химических и биологических системах в 1966 году в Пущино97.
Уже к этому времени С.Э. Шноль и его коллеги пришли к выводу, что наблюдаемый ими "разброс результатов" не является следствием каких-либо кинетических колебательных процессов и что речь идет скорее не о колебаниях, а о флуктуациях, которые могут охватывать макроскопические объемы и происходить одновременно в разных частях сосудов с растворами белка /Шноль, 1965/. “Поскольку при наблюдавшихся флуктуациях изменялась не только ферментативная активность, но и число титрируемых SН-групп, было предположено, что "макроскопические флуктуации" являются следствием синхронных изменений конформации макромолекул белков” /Удальцова и др., 1987, с.4-5/. При этом предполагалось, что синхронизация конформационных колебаний молекул фермента во всем объеме раствора является следствием взаимодействия макромолекул через разделяющую их среду /Шноль, 1969/.
Исходя из этих представлений, С.Э. Шноль и его сотрудники долгое время рассматривали обсуждаемый феномен как "конформационные колебания" макромолекул белка и изучали зависимость амплитуды этих колебаний как от свойств самих макромолекул, так и от свойств разделяющей их среды - водного раствора. С этой целью исследовали влияние на конформационные колебания факторов - химических и физических, направленных как на макромолекулы белка, так и на разделяющий их растворитель. Результаты этих исследований были опубликованы в период 1964-1979 гг.98
Длительное время предполагалось, что "конформационные колебания" представляют собой специфическое свойство лишь фибриллярных белков актомиозинового комплекса. Однако в 1966 г. были обнаружены колебания (флуктуации) в растворах глобулярного белка - фермента креатинкеназы /Четверикова и др., 1967/. В дальнейшем на основе больших серий опытов с множеством разных препаратов было показано, что “"макроскопические флуктуации" являются общим свойством всех белков” /Шноль, Иванова и др., 1980/. При этом выяснилось, что макроскопические флуктуации не проявляются при денатурации белков /Рыбина и др., 1979/.
Однако исследования постепенно вышли за пределы белковых препаратов, поскольку выяснилось, что аналогичные "макроскопические флуктуации" наблюдаются и в безбелковых системах, и в частности, в колебаниях реакционной способности при взаимодействиях аскорбиновой кислоты с дихлорфеноминдофенолом /Рыбина и др., 1979/. Поэтому уже в 1980 г. сформировалось мнение, что “нативные макромолекулы белков являются лишь индикаторами идущих и без них макроскопических флуктуаций” /Удальцова и др., 1987, с.5/. И действительно, к 1982 г. макроскопические флуктуации (МФ) были обнаружены при измерениях таких разных процессов, как электрофоретическая подвижность клеток и частиц латекса, времени спин-спиновой релаксации Т2 протонов воды, флуктуации спектральной чувствительности глаза, времени разряда КС-генератора на неоновой лампе, а также при измерениях радиоактивного распада. Выяснилось, что большое сходство обнаруживают гистограммы МФ не только качественно различных процессов, исследуемых в одной лаборатории, но и процессов, исследуемых в лабораториях, отстоящих друг от друга на тысячи километров. Синхронными оказались и изменения гистограмм макрофлуктуаций разных и, в том числе, разнесенных на большие расстояния, процессов. Выявленные особенности макрофлуктуаций навели исследователей на мысль о том, что это явление имеет какие-то глобальные космофизические причины (См.:/Шноль и др., 1985; Удальцова и др., 1987/).
При этом были обнаружены весьма интересные особенности этого феномена.
1/ "Эффект места". В процессе исследования было обнаружено устойчивое различие характеристик макрофлуктуаций при измерениях в разных местах лабораторного помещения. Характеризуя этот эффект, авторы пишут: “Устойчивые воспроизводимые различия формы гистограмм наблюдались в многодневных опытах при помещении сосудов с соответствующими растворами на разные места одного и того же лабораторного стола, при расстоянии между сосудами около 30-40 см. Эти "эффекты места" не исчезали при экранировании сосудов стальными, заземленными экранами и не изменялись в зависимости от расположения в лабораторном помещении магнитов, трансформаторного железа, нагревательных приборов...” /Удальцова и др., 1987, с.17/.
Авторы указывают на то обстоятельство, что существенные различия гистограмм измерений образцов, стоящих на одном лабораторном столе, сочетаются с высокой степенью совпадения формы гистограмм результатов измерений МФ разных процессов на расстояниях в сотни и тысячи километров.
Дело обстоит так, как если бы пространство имело такую ячеистую структуру, в которой каждая ячейка дает вполне определенную форму гистограмм макроскопических флуктуаций качественно различных процессов и явлений, находящихся в этой ячейке. Авторы предположить, что существует небольшое число разных вариантов этих ячеек и достаточно велика вероятность того, что на больших расстояниях исследуемые объекты оказываются в одинаковых ячейках пространства, дающих при синхронных измерениях одинаковые формы гистограмм макрофлуктуаций.
2/ Попытки экранировать исследуемые объекты при помощи экранов из разных материалов привели исследователей к выводу о том, что эти явления не обусловлены электромагнитными полями, поскольку не обнаружено соответствующей зависимости от материала экрана /Удальцова и др., 1987, с.17/.
3/ Интересные результаты получены при исследованиях корреляции параметров МФ с космофизическими процессами. Так, оказалось, что для биохимических и химических процессов среднегодовые значения макрофлуктуаций изменяются противофазно характеристике солнечной активности, т.е. “в годы с высокой солнечной активностью средняя амплитуда МФ была низкой и, наоборот, в годы низкой солнечной активности наблюдался весьма большой "разброс результатов" измерений биохимических и химических процессов” /Там же, с.19/. Авторы при этом отмечают, что из всех известных космофизических процессов в такой же зеркальной противофазности к солнечной активности находится интенсивность потока нейтронного компонента галактических космических лучей.
С точки зрения возможности синхронизации процессов протекающих в разных клетках живого организма, большой интерес представляют проведенные в 1951-1961 годах исследования концентрации различных веществ в крови живых организмов /Шноль, Гришина, 1964/. Обнаруженные в этих опытах резкие флуктуации содержания в крови разных веществ “пытались объяснить ритмической активностью печени, поглощающей и отдающей в кровоток различные вещества, или же ритмическим изменением адсорбционной способности эндотелия кровеносных сосудов” /Удальцова и др., 1987, с.66/. Рассматривая результаты этих исследований в свете открытых позже макрофлуктуаций, Н.В. Удальцова, В.А. Коломбет и С.Э. Шноль отмечают, что “... самым удивительным в тех опытах была необъяснимая синхронность изменений в концентрации крови различных веществ у разных животных”99, и пишут, что теперь на основе результатов исследований феномена макрофлуктуаций “эту синхронность можно объяснить общей внешней причиной, одновременно изменяющей, например, адсорбционную способность (электрический заряд) эндотелия сосудов разных животных” /Там же/.
Но если имеет место синхронизация биохимических и биофизических процессов, протекающих в разных организмах, то тем более правомерно предполагать возможность синхронизации одинаковых процессов, протекающих в разных клетках одного и того же организма.
Несмотря на более чем 30-летний срок исследований макроскопических флуктуаций (МФ), этот феномен еще до сих пор не получил своего удовлетворительного объяснения. Можно лишь считать достаточно обоснованным вывод о том, что под влиянием каких-то космических "сил" все объекты окружающего нас макромира постоянно меняют свои состояния, что проявляется в виде макроскопических флуктуаций тех или иных характеристик этих объектов и протекающих в них физических и химических процессов.
Результаты исследований лаборатории С.Э. Шноля не оставляют сомнений в том, что, какова бы ни была природа этих сил, МФ могут иметь важное значение для временной организации физиологических процессов, выступая в качестве фактора, обеспечивающего синхронизацию однотипных процессов, протекающих в разных клетках многоклеточного сложного живого организма. При этом речь идет не о том, что эти процессы должны синхронизироваться в обычном физическом времени. В данном случае "синхронизация" означает, что многоступенчатые циклические процессы в разных клетках протекают таким образом, что одни и те же их ступени в разных клетках протекают когерентно, т.е. одномоментно, хотя при этом длительности как всего цикла, так и отдельных его этапов не остаются постоянными величинами в единицах физического времени, а меняются случайным, однако, одинаковым для всех клеток образом. Если такая синхронизация однотипных колебательных процессов живого организма имеет место в действительности, то введенное выше понятие внутриклеточного метаболического времени может оказаться предельно мелким масштабом (“ тонкой структурой” ) биологического времени сложных живых организмов как единых целостных систем.
Таким образом, имеются определенные основания предполагать синхронное следование квантов биологического времени во всех клетках многоклеточного живого организма. Это позволяет подойти к решению проблемы одновременности пространственно удаленных друг от друга процессов живого организма принципиально иначе, чем аналогичная проблема решается в физическом мире.
Как известно, в абсолютном времени классической физики существовала абсолютная одновременность событий, протекающих в сколь угодно удаленных друг от друга точках мирового пространства. Это означало, что все события мироздания однозначно делятся на прошедшие, настоящие и будущие.
Подобные представления оставались общепринятыми, пока не появилась позитивистская идея о необходимости их экспериментальной проверки и обоснования. Анализ показал, что в их основе лежит только априорная уверенность в том, что одновременными являются те события, которые могут быть охвачены единым актом сознания. В реальной действительности абсолютная одновременность и однозначное деление всех событий на прошедшие, настоящие и будущие оказываются эмпирически достоверными только при условии, что взаимодействие и обмен информацией между событиями происходит с бесконечной скоростью. При любых конечных скоростях взаимодействия требование эмпирической проверяемости временных отношений между событиями приводит к появлению класса событий, между которыми не существует отношения "раньше (позже), чем", и характер временных отношений между ними оказывается неопределенным.
В специальной теории относительности (СТО) одновременные пространственно удаленные друг от друга события выявляются в ходе синхронизации связанных с этими событиями часов. Предложенная А. Пуанкаре и использованная А. Эйнштейном при разработке СТО процедура синхронизации пространственно удаленных друг от друга часов сводится к следующему.
Пусть в точке А имеются некоторые часы и "точно такие же часы" имеются в точке В. Тогда наблюдатели в точках А и В будут фиксировать события в "А-времени" и "В-времени". Общее для точек А и В время, считает А. Эйнштейн, можно установить, если ввести определение, что "время", необходимое для прохождения света из А в В, равно "времени", требуемому для прохождения света из В в А /Эйнштейн, СНТ, т., 1, с. 9/. Пусть в момент ![]() по "А-времени" луч света выходит из А в В, отражается в момент
по "А-времени" луч света выходит из А в В, отражается в момент ![]() по "В-времени" от В к А и возвращается назад в А в момент
по "В-времени" от В к А и возвращается назад в А в момент ![]() по "А-времени".
по "А-времени".
При этих условиях практически добиться того, чтобы часы в точках А и В показывали одно и то же время, можно следующим образом. Пусть между наблюдателями, находящимися в точках А и В, имеется договоренность о том, что наблюдатель в точке В в момент отражения сигнала от В к А выставляет на своих часах заранее договоренное с наблюдателем точки А показание, например, 00 часов, 00 минут, 00 секунд. В этом случае наблюдатель в точке А знает, что часы в точке В в момент (![]() -
- ![]() )/2 по часам точки А показывают 00 часов, 00 минут, 00 секунд, и может соответствующим образом скорректировать показания своих часов. В современной физике предполагается, что одинаковым образом изготовленные и синхронизированные между собой часы, находясь в разных точках инерциальной системы отсчета, будут неограниченно долго показывать одинаковое время.
)/2 по часам точки А показывают 00 часов, 00 минут, 00 секунд, и может соответствующим образом скорректировать показания своих часов. В современной физике предполагается, что одинаковым образом изготовленные и синхронизированные между собой часы, находясь в разных точках инерциальной системы отсчета, будут неограниченно долго показывать одинаковое время.
Именно такой смысл вкладывает А. Эйнштейн в понятие одновременность. Вполне естественно, что если указанным выше образом синхронизировать часы во всех точках инерциальной системы отсчета, то все они будут одномоментно показывать одно и то же время, и мы введем некоторый аналог абсолютного времени, в котором существует "абсолютная одновременность" (одни и те же показания часов) и однозначное деление всех событий на прошедшие, настоящие и будущие. Однако подобная "одновременность" событий в масштабах всей инерциальной системы не имеет в физическом мире практического значения, поскольку при таком способе разграничения всех событий на прошедшие, настоящие и будущие далеко не для всех событий разнесенность их в разные времена означает возможность установления однозначных причинно-следственных связей между ними. Так, например, все события, которые имели место в точке А в период, начиная с момента посылки светового сигнала в точку В и до возвращения в точку А отраженного сигнала, не могут иметь причинно-следственных связей с событиями, которые имели место в точке В в момент отражения пришедшего из точки А светового сигнала.
В литературе, посвященной философским проблемам теории относительности, понятие “ одновременность” получило более широкое толкование, а именно, как совокупность таких событий, между которыми не может быть причинно-следственных связей, а следовательно, и однозначных временных отношений, если временные отношения между событиями связывать с реальными или, по крайней мере, потенциально возможными между ними причинно-следственными связями. При таком причинном определении временной последовательности событий все те события, между которыми не могут существовать материальные взаимодействия, можно рассматривать как релятивистский аналог “ всемирной одновременности ньютоновской физики” /Уитроу, 1964, с. 389/ и называть либо “ квазиодновременными” /Фок, 1961, с. 52/, либо “ топологически одновременными” /Грюнбаум, 1969, с. 44-48, 435-505/. Учитывая это, мы назовем одновременность, определенную как одинаковые показания синхронизированных между собой часов, “ формальной одновременностью” .
В физическом мире “ формальная одновременность” не имеет физического смысла. Совершенно иначе обстоит дело в живом организме, в котором каждая клетка содержит копию одной и той же генетической программы, и если эта программа закодирована в единицах метаболического времени, то при существовании формальной одновременности все клетки организма могут точно одновременно совершать те или иные акты при условии, что счет времени ведется непрерывно с самого начала эмбрионального развития организма.
Итак, мы рассмотрели некоторые данные современной биологии, позволяющие сделать вывод о том, что биологические процессы живого организма структурированы в особом биологическом времени.
Наиболее глубинным, фундаментальным уровнем временной организации биологических процессов живой материи является уровень ферментативных реакций внутриклеточного метаболизма. Именно здесь необходимо искать далее неделимые кванты биологического времени, на протяжении которых протекающие в весьма своеобразно организованной и резко изменяющей свои свойства внутриклеточной среде физические и физико-химические процессы интегрируются в элементарные акты биологических процессов.
Квантованность биологического времени может иметь важное значение для генетики, а также для теоретической биологии. Однако для целей практического хронометрирования биологических процессов необходимо искать более крупные единицы биологического времени, связанные с его квантами через постоянные масштабные коэффициенты. При этом не исключено, что может не оказаться таких доступных практическому счету единиц биологического времени, которые сохранялись бы на всех этапах развития живого организма100.
В настоящей работе нами обоснована принципиальная возможность существования качественно различных форм времени и показана правомерность введения в биологию понятия биологического времени. Однако проблема биологического времени нуждается в дальнейшей экспериментальной, теоретической и методологической разработке, поскольку введение в понятийный аппарат биологии понятия биологического времени - это серьезный шаг, требующий решения сложных и трудоемких задач, связанных с разработкой систем единиц биологического величин, установлением специфических законов биологической формы движения материи, а также с разработкой принципиально новых приемов и методов исследования живой материи.
72 “Внутренние переменные организмов вместе с существенными параметрами среды исчисляются сотнями и тысячами” /Уотермен, 1968, стр. 12/.
73 Так, например, М. Дельбрюк писал, что “зрелого физика, впервые сталкивающегося с проблемами биологии, ставит в тупик то обстоятельство, что в биологии нет "абсолютных явлений". Каждое явление представляется иным в разных местах и в разное время” (Цит. по: /Майр, 1970, с.48/).
74 См., например: /Уотсон, 1971, с. 267-295/.
75 К 60-70-м годам были уже составлены метаболические карты животных, микроорганизмов и растений. В 70-е годы вышло ряд фундаментальных работ, посвященных анализу метаболических путей живых организмов. См., например: /Гилмур, 1968; Малер, Кордес, 1970; Гофман, 1971; Дэгли, Никольсон, 1973 и др./. Образно сравнивая отдельные биохимические реакции с нотами в партитуре симфонии, Д. Гилмур писал: “...Одни и те же ноты повторяются много раз, но звучание оркестра разнообразно до бесконечности. Столь же изменчива в целом и система молекулярных превращений, которую мы называем метаболизмом” /Гилмур, 1968, с 10/.
В дальнейшем была предпринята попытка систематизировать метаболические процессы живых организмов в виде периодических сетей. См.: /Малыгин, 1976; 1984/.
76 Так, например, Г. Малер и Ю. Кордес писали: “...Теперь мы знаем, что клетка состоит из множества разнообразных взаимосвязанных элементов, обладающих весьма сложной структурой и организацией. Эти элементы могут варьировать у разных организмов, в разных тканях и в разных типах клеток. Однако во всей этой сложной картине можно уловить определенный порядок: хотя в действительности и не существует такого образования, как типичная клетка, почти всем клеткам, по-видимому, свойственны некоторые общие черты. Можно указать некоторые общие субклеточные структуры, которые, очевидно, являются гомологичными в морфологическом, топологическом, а возможно, и в функциональном отношении во всех клетках независимо от их происхождения” /Малер, Кордес, 1970, с. 240/.
77 “Под сокрушительным напором лавины новых фактов и идей, - писал Б.Л. Астауров, - возникла настоятельная потребность в переосмысливании всей гигантской совокупности накопленных биологией знаний, и задача построения теоретической биологии приобрела особую остроту”. И далее, характеризуя существовавшую в конце 60-х годов постановку вопроса о построении теоретической биологии, он замечает: “Теперь, говоря о "теоретической биологии", в это выражение начинают вкладывать примерно тот же смысл, какой вкладывают, говоря о теоретической физике, разумея под задачами теоретической биологии познание самых фундаментальных и общих, но в то же время специфических свойств и законов, присущих той качественно особой форме движения материи, которую мы именуем жизнью” /Астауров, 1970, с. 5,6/. См. также: /Астауров, 1972, с. 61, 62/.
78 О необходимости создания теоретической биологии писали Дж. Бернал, Б.Л. Астауров, В.А. Энгельгардт и др. Так, Дж. Бернал, отмечая, что современная биология занимается описанием и систематизацией фактов и больше похожа на географию, чем на физику, выражал уверенность, что будет создана "подлинная и общая" "истинная биология", которая по глубине основных принципов, широте охвата жизни и мощи средств и методов исследования и описания живой материи будет сравнима с современной теоретической физикой, и биология, наконец, станет “наукой о природе и активности всех организованных объектов, где бы они ни находились - на нашей планете, на других планетах солнечной системы, в иных звездных системах или других галактиках, и во все времена, будущее и прошлое” /Бернал, 1968, с. 111/.
79 Без особого преувеличения можно утверждать, что в 60-70-е годы клеточная теория переживала вторую молодость и многие традиционные проблемы биологии, рассматривавшиеся до этого на уровне всего целостного организма или отдельного его органа, начали пересматриваться "с позиции клетки". Эта тенденция достаточно ярко отразилась, например, в таком капитальном труде, как монография Э. де Робертиса, В. Новинского и Ф. Саэса , /Робертис и др., 1967/.
80 Так, были выявлены и детально изучены многие составные элементы внутриклеточной структуры вплоть до молекулярного уровня, раскрыты структуры многих биохимических процессов внутриклеточного метаболизма, установлена тесная взаимосвязь между многими биохимическими и биофизическими внутриклеточными процессами, и складывалось достаточно четкое представление о том, что клетка - это целостная интегрированная система, которая “...не может функционировать, воспроизводить себя и развиваться без какого-либо из своих элементов” и в которой, “с другой стороны, ни один из элементов... не автономен полностью, а постоянно подчинен системе в целом” /Нейфах, 1967, с.3/.
81 Так, например, Н.А. Бернштейн, анализируя пути применения математики для описания поведения живых организмов, делал, на наш взгляд, слишком общий и излишне категорический вывод о том, что “на путях математизации биологических наук речь должна идти не о каком-то приживлении или подсадке к биологии извне (именно такие попытки делались и, несомненно, еще будут делаться и впредь), а о выращивании новых, биологических глав математики изнутри, из самого существа тех вопросов, которые становятся перед науками о жизнедеятельности” /Бернштейн, 1965, 10, с. 78/.
82 Как совершенно справедливо пишет В.Б. Касинов: “В теоретической биологии... нет ничего собственно биологического, за исключением объектов - живых систем. Весь идейный, концептуальный багаж биологов-теоретиков заимствован извне, а не создан на почве самой биологии. Основой этого багажа служит физическое мировоззрение, физические представления о времени, пространстве, движении, атомах, полях и т.д.” /Касинов, 1979, с. 4/.
83 Идею подобного моделирования клетки развивали, например, Д. Грин и Р. Гольдбергер, которые считали, что необходимый для любой клетки минимальный комплект оснащения должен включать: 1/ систему мембран, которые окружают клетку, разделяют ее на отсеки, управляют химическим хозяйством и несут на себе ряд важных катализаторов клетки; 2/ аппарат для получения точных копий клетки путем копирования ее основных структур; 3/ аппарат, обеспечивающий клеточные функции энергией, получаемой в результате окислительных процессов /Грин, Гольдбергер, 1968, с. 13/.
84 Как совершенно справедливо пишет А.У. Игамбердиев: “Парадигма современной биологической науки связана преимущественно с редукционистским способом мышлением, который наибольшее влияние оказывает на самые передовые отрасли биологии и прежде всего на молекулярную биологию. Основополагающие открытия, сделанные в этой области, имея важнейшее значение для понимания механизмов биологических явлений, практически не затронули проблему биологического движения, которое рассматривается чисто механистически” /Игамбердиев, 1985, с. 471/.
85 Объектами исследований Т.А. Детлаф и ее коллег являются только пойкилотермные животные. Но если учесть, что историческими предками современных гомойотермных (теплокровных) животных были пойкилотермные живые организмы и что ко времени возникновения гомойотермных животных характерные для пойкилотермных животных механизмы регулирования скорости биологических процессов и темпов развития при изменениях температурных и других характеристик внешней среды уже были зафиксированы в генетическом аппарате и передавались по наследству, то можно будет предположить, что биологические процессы и у теплокровных животных внутренне структурированы так же, как и у пойкилотермных животных. Отличие, видимо, заключается в том, что у гомойотермных животных весьма сужены границы оптимальных температур, в пределах которых выполняется закон пропорциональности изменений темпов биологических процессов при изменениях температуры организма.
86 См. графики зависимости “ детлаф” от температуры среды для разных пойкилотермных живых организмов в работах: /Детлаф и др., 1993; Давыдов и др., 1989; Детлаф, 1986; Мазин и др., 1985; Игнатьева, 1979; Костомарова и др., 1968/.
87 Предположение о том, что измеряемое “ детлафами” биологическое время есть результат аффинного преобразования физического времени, было высказано Л.Н. Любинской /Детлаф, Любинская, 1987/
88 На неудовлетворительность аппроксимации живых организмов статистическими моделями обращают внимание многие исследователи. Так, например, В.А. Карасев, В.Е. Стефанов и Б.И. Курганов пишут, что такие модели “охватывают лишь часть функций системы (к тому же при заданных внешних условиях) и поэтому не могут использоваться для доказательства адекватности статистического подхода” /Карасев и др., 1989, с.12/. Э. Шредингер считал, что тенденция неживой материи переходить к неупорядоченности связана со статистическим характером физических законов, тогда как живая материя подчиняется динамическому типу физического закона /Шредингер, 1972/. На ограниченность статистического описания протекающих в живых организмах процессов указывали и другие авторы.
Отвечая на вопрос о том, что обеспечивает неподчинение живых систем статистическим законам физики, В.А. Карасев, В.Е. Стефанов и Б.И. Курганов пишут, что “законы статистики действуют только в системах, содержащих мириады частиц”, тогда как живые системы обладают высоким уровнем организации, в которой “"микрокомпартментализация", т.е. локализация процессов в малом объеме, где действует малое число частиц, по сравнению с тем, которое необходимо для статистического описания” /Там же, с.13/, определяет способность поддерживать упорядоченность и избегать равновесия.
Можно вполне согласиться с выводом авторов о том, что “микрокомпартментализация является необходимым условием организации жизни” /Там же, с.13/, однако вовсе не по тем причинам, на которые они при этом указывают. Различие между динамическими и статистическими системами обусловливается не количеством частиц в них, а характером протекающих процессов. Статистические законы характеризуют вероятностные, стохастические системы. Недостаточное для проявления закона больших чисел количество частиц ведет, в общем случае, не к подчинению систем динамическим законам, а просто к невозможности установить статистические законы. Система же при этом как была статистической, т.е. подчиняющейся статистическим законам, так таковой и остается. Микрокомпартментализация процессов в живых клетках важна тем, что она обеспечивает условия, благоприятные для синхронизации протекающих в этих малых объемах ферментативных процессов.
Серьезным аргументом в пользу подчинения протекающих в живых организмах процессов динамическим законам является апелляция авторов к представлениям о живом организме как о высокоорганизованном кристаллоподобном теле /Карасев и др., с.13/. При этом они исходят из положения Э. Шредингера о том, что система может подчиняться динамическому закону, если она состоит из твердых тел, форма которых удерживается химическими связями между ее атомами. Авторы отмечают, что Э. Шредингер обосновывал подчинение живых систем динамическому закону тем, что в основе организма находится твердое тело - ген, который он называл "апериодическим кристаллом". Современные же исследования приводят многих ученых к выводу о том, что подобным "апериодическим кристаллом" является весь сложный живой многоклеточный организм, или, как пишут В.А. Карасев, В.Е. Стефанов и Б.И. Курганов: “...весь организм является высокоупорядоченным кристаллоподобным телом, все атомы которого связаны в единую механическую систему” /Карасев и др., с.13/.
89 Значение данной идеи заключается в том, что при составлении уравнений, описывающих в определенном масштабе времени состояние материальной системы, переменные, зависящие от слишком быстрых процессов, при некоторых условиях можно усреднять и рассматривать либо как постоянные, либо как весьма медленно изменяющиеся параметры. Равным образом и переменные, зависящие от достаточно медленных процессов, войдут в уравнения как постоянные параметры. При этом оказывается, что процессы, обладающие разными временами релаксации и относящиеся к разным масштабам времени, требуют и различного описания. Эта идея была использована Н.Н. Боголюбовым при построении теории неравновесных процессов в газах (См.: /Боголюбов, 1946/). Подробный анализ идеи Н.Н. Боголюбова можно найти в статье Г.Е. Уленбек /Уленбек, 1965/.
Применительно к биологическим системам идея разделения процессов в соответствии с их временами релаксации выдвинута Уоддингтоном (См.: /Waddington, 1957/).
90 В этой связи следует напомнить, что нарушающие симметрию мира бесконечно малые возмущения играют важную роль в теории необратимых процессов (См.: /Зубарев, 1970/).
91 Подробную библиографию работ по рассматриваемой проблеме см.: /Удальцова, Коломбет, Шноль, 1987/.
92 С.Э. Шноль отмечает, что представление о существенной энергетической роли макромолекул в ферментативном катализе далеко не новы, и анализирует соответствующие взгляды Э. Бауэра, Мелвин-Хьюза, Кобозева и др. авторов /Шноль, 1967, с. 27-30/.
93 В настоящее время имеются полученные при помощи лазерной техники прямые доказательства того, что в ходе каталитической деятельности молекулы фермента претерпевают циклический ряд конформационных изменений.
94 Как известно, атомы водорода в молекуле воды смещены в одну сторону, и угол между прямыми, соединяющими центры их ядер с центром ядра кислорода, составляет 120![]() .
.
95 В настоящее время синхронизация колебательных процессов рассматривается как одна из наиболее распространенных “форм самоорганизации материи” /Блехман, 1981, с. 7/ и представляет собой “свойство материальных объектов самой различной природы вырабатывать единый ритм совместного существования, несмотря на различие индивидуальных ритмов и на подчас крайне слабые взаимные связи” /Там же/.
Обобщая открытые за последние десятилетия многочисленные формы проявления когерентных излучений и состояний вещества, Л.Н. Шелепин пишет, что явление когерентности далеко выходит за рамки одного или нескольких разделов физики и носит общий, глобальный характер. Автор высказывает мнение, что понятие когерентности начинает приобретать фундаментальный общенаучный характер и по своему статусу приближается к философским категориям /Шелепин, 1980, с. 449, 450-451/. См. также: /Акчурин, 1985/.
96 Полученные в лаборатории С.Э. Шноля результаты, имея под собой достаточно солидную и весьма надежно обоснованную экспериментальную базу, выглядят тем не менее весьма необычными. Поэтому в научном мире к ним наблюдается настороженное отношение: хотя нет сколь-либо серьезных попыток опровергать их, но нет и каких-либо тенденций признать обнаруженные феномены и заняться поисками путей их теоретического объяснения. Учитывая это, мы в данной работе постараемся как можно более точно изложить полученные в лаборатории С.Э. Шноля результаты.
97 См. статьи С.Э. Шноля и других исследователей в сб.: Колебательные процессы в биологических и химических системах. - М.: Наука, 1967.
98 См. библиографию в работе: /Удальцова, Коломбет, Шноль, 1987, с. 5/