Детерминационный анализ как метод диагностики состояния экосистемы
В.Н.Максимов, Н.Г.Булгаков и А.П.Левич
Кафедра общей экологии, Биологический факультет, МГУ им. М.В. Ломоносова, Воробьевы горы, 119899 Москва, Россия. Тел.: (095)939-5560. E-mail:
![]()
1. ВВЕДЕНИЕ
Фундаментальные знания о закономерностях функционирования естественных надорганизменных систем добывают не только в специально организованных и спланированных экспериментах, но и путем анализа данных экологического мониторинга, полученных с помощью стандартных методик. Эти данные накапливаются десятилетиями, могут охватывать большие территории, но не всегда удовлетворяют требованиям метрологии, статистической воспроизводимости и другим условиям, которые позволили бы обоснованно использовать для их анализа традиционные методы математической статистики.
Анализ экологической литературы последних лет (Будилова и др., 1995) показывает, что при анализе многомерных массивов данных, получаемых в ходе исследования природных экосистем, чаще всего применяются либо классические статистические методы, такие как дисперсионный и регрессионный анализ, либо методы, лишь формально относящиеся к статистическим: факторный анализ, кластер-анализ, многомерное шкалирование. Благодаря тому, что для всех этих методов в настоящее время имеются пакеты прикладных вычислительных программ (например SYSTAT, SPSS, STATISTICA и др.), эти методы стали доступны для широкого круга экологов, как правило не имеющих адекватной математико-статистической подготовки. Между тем применимость указанных методов к анализу данных экологических наблюдений (экологического мониторинга), относящихся к категории т.н. "пассивных экспериментов", представляется достаточно проблематичной.
Известно, в частности, что регрессионный и дисперсионный анализ базируются на ряде довольно жестких предпосылок, из которых назовем 3 наиболее важных: 1) результаты наблюдений должны быть независимыми случайными величинами, распределенными нормально; 2) выборочные оценки наблюдений должны быть однородны, т.е. не должны зависеть от величины результатов наблюдений; 3) ошибки в определении независимых переменных должны быть в идеальном случае равны нулю или, по крайней мере, пренебрежимо малы по сравнению с ошибкой в определении величины результатов наблюдений.
Многолетний опыт работы с данными экологического мониторинга убеждает в том, что для них ни одна из этих предпосылок не выполняется. Однако если затруднения, связанные с первыми двумя предпосылками, можно преодолеть путем "нормализующих" преобразований величины результатов наблюдений, то выполнение 3-го требования практически неосуществимо, поскольку погрешности в определении таких переменных, как численности видов, концентрации биогенных элементов и т.п. - связаны не столько с несовершенством методик, сколько с неоднородностью ("пятнистостью") распределения этих показателей в пространстве реальных биотопов.
К этому следует также добавить, что даже при выполнении всех вышеперечисленных предпосылок статистические модели вообще и регрессионные модели в частности не могут быть использованы для установления или доказательства наличия причинно-следственных связей в изучаемой системе. Еще Дж.Ацци (Azzi, 1928) предостерегал от бездумной интерпретации значимости коэффициентов корреляции, как доказательства причинной связи между коррелирующими переменными. Много лет спустя Д.Хейс сформулировал ту же мысль еще более резко: "На уравнения регрессии нельзя смотреть шаблонно, как на структурные уравнения, непосредственно представляющие причинные процессы" (Д.Хейс, 1980, стр.105). Убийственный (для применения регрессии при анализе результатов пассивных экспериментов) пример приведен в книге В.В.Налимова и Н.А.Черновой (1965). При решении задачи описания системы, гораздо более простой, чем экосистема, — химического процесса, в котором выход некоторого продукта зависел только от 3-х переменных, было получено 11 уравнений регрессии, от линейного до неполного уравнения 3-й степени, для каждого из которых коэффициент множественной корреляции был близок к 0.9, так что невозможно сделать выбор "наилучшей" или "наиболее адекватной" модели. Приходится согласиться с мнением авторов:" Не имеет никакого смысла придавать какое-либо значение индивидуальным коэффициентам регрессии" (Налимов, Чернова, 1965, стр. 29). Впрочем приходится также констатировать, что это мнение осталось неизвестным для большинства экологов как у нас, так и за рубежом.
Независимо от конечных целей экологического мониторинга и организации соответствующей системы наблюдений результат этих наблюдений всегда представляет собой прямоугольную таблицу. Если значения измеряемых переменных располагать в столбцах, число таких столбцов может достигать нескольких десятков — по числу переменных. Каждая строка в такой матрице будет содержать измеренные значения упомянутых переменных в одной пробе, отобранной в определенный момент времени в определенном месте. Понятно, что число таких строк может измеряться сотнями. Иначе говоря, исходные данные, полученные по программе мониторинга, представляют собой матрицу размерности m*n, где m — число строк, n — число столбцов, и размерность эта весьма велика.
При работе с такими матрицами специалисты по статистическому анализу экспериментальных данных рекомендуют использовать разнообразные методы многомерной статистики. Преимущества этих методов по-видимому бесспорны: 1) вместо изучения каждой из переменных в отдельности и ее связей с остальными можно сразу исследовать весь массив данных и получить информацию о влиянии всех переменных и их взаимодействий на изучаемую экосистему; 2) при нынешней всеобщей компьютеризации снимаются все затруднения, связанные с огромным объемом вычислений. Раньше многомерными статистическими методами могли пользоваться лишь сравнительно немногие исследователи, в распоряжении которых были большие вычислительные машины и при них помощники-программисты. Теперь не менее (а то и более) мощный персональный компьютер стоит у каждого экспериментатора на письменном столе, а современные (и весьма популярные!) пакеты прикладных статистических программ, такие как Стадия, Statgraphics, Systat, SPSS, и т.п., позволяют осуществлять анализ данных даже в том случае, когда исследователь имеет лишь приблизительное представление об алгоритме соответствующих вычислений и принципах его построения. Достаточно создать файл исходных данных и "загрузить" подходящий программный модуль из пакета, которым данный пользователь располагает, руководствуясь в высшей степени "дружественным интерфейсом", которым снабжен каждый такой пакет.
Однако в этой кажущейся простоте заключена и немалая опасность, поскольку далеко не всегда исходные данные удовлетворяют тем, довольно жестким, требованиям, которые предъявляют к ним стандартные статистические методы. В учебниках по статистике эти требования, естественно, всегда оговариваются. Важнейшие из них — нормальность распределений переменных, однородность дисперсий, устойчивость частот. Однако ни в одном из таких учебников мы не видели указаний на то, к чему приводит нарушение этих требований.
Необходимо также заметить, что традиционные статистические подходы часто не приспособлены к обработке данных, сочетающей числовые и нечисловые (качественные) переменные, к совместному анализу данных по объектам разной природы и разных уровней описания, к анализу нелинейных и неквазилинейных взаимосвязей переменных, хотя именно нелинейные связи преобладают в реальных экосистемах.
Многие недостатки традиционной статистики не свойственны методу детерминационного анализа (ДА), который оперирует лишь условными частотами многомерных событий, не обращаясь к коэффициентам корреляции или ковариации, к мерам близости и связи, т.е. к обычному инструментарию математической статистики, которая налагает слишком жесткие требования на исходные данные.
К настоящему моменту накоплен достаточный опыт применения детерминационного анализа в гуманитарных науках, в частности, в социологических исследованиях (Чесноков, 1982). Кроме того, авторами предприняты первые шаги для адаптации метода в биологических исследованиях (Замолодчиков и др., 1992; Булгаков и др., 1992; Левич и др., 1996).
2. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ДЕТЕРМИНАЦИОННОГО АНАЛИЗА ЭКОЛОГИЧЕСКИХ ДАННЫХ
Причинно-следственные закономерности обычно описываются суждениями вида "если X, то Y". Например, в экосистемах X может быть совокупностью значений некоторого комплекса факторов, а величина Y - характеризовать состояния экосистемы. Одна из особенностей функционирования сложных систем состоит в том, что подобные суждения имеют условный характер: в ряде случаев суждение оказывается истинным, в ряде - ложным. Степень достоверности суждения, очевидно, определяется частотой E, с которой состояние Y встречается в эмпирических данных среди всех случаев, когда исследуемый комплекс факторов имеет значение X, и частотой C, с которой совокупность значений факторов X встречается в эмпирических данных среди всех случаев, когда экосистема имеет состояние Y. E носит название точности, а C - полноты суждения "если X, то Y". Эти величины являются условными частотами события (X,Y) (Чесноков, 1982). Условные суждения представляют собой способ описания, частным случаем которого являются строгие и однозначные функциональные зависимости Y(X), имеющие место при изучении "хорошо организованных" (обычно лабораторных) экспериментов (точность и полнота таких зависимостей стопроцентны).
Таким образом, метод детерминационного анализа оперирует лишь условными частотами многомерных событий, не обращаясь к коэффициентам корреляции или ковариации, к мерам близости и связи, т.е. к обычному инструментарию математической статистики, которая налагает слишком жесткие требования на исходные данные.
Точность и полнота правила "если X, то Y" может характеризовать значимость взаимной сопряженности событий X и Y. Представляет интерес и исследование приращений условных частот при изменении набора факторов. Такие приращения могут характеризовать существенность факторов и их комплексов в исследуемых закономерностях. Техника анализа условных частот легко позволяет проводить межмассивную обработку данных, а именно - рассчитывать достоверность правила "если X, то Z", когда известны достоверности правил "если X, то Y" и "если Y, то Z", а массив экспериментальных данных, включающий переменные X и Z одновременно, отсутствует.
Предлагаемый анализ условных частот и их приращений позволяет эффективно решать задачи распознавания образов в многомерных пространствах данных: строить кластеры, типологии, таксоны; конструировать агрегированные переменные, интегральные показатели и т.п. (дополняя тем самым метод главных компонент, факторный анализ, многомерное шкалирование и другие подобные методы многомерной статистики).
В области экологических исследований анализ точности, полноты, существенности взаимосвязей между характеристиками экосистем, кроме стандартной задачи проверки гипотез о взаимном влиянии переменных, позволяет с помощью процедуры оптимизации отыскивать границы области нормального функционирования в пространстве экологических факторов и вычислять экологически допустимые уровни (ЭДУ) абиотических факторов, влияющих на экологическое состояние биотических компонентов экосистем (Левич, 1994; Левич, Терехин, 1997; Maximov et al., 1999). Найденные ЭДУ могут использоваться в задачах экологического нормирования, районирования и прогноза как региональные нормативы воздействий, нарушающих экологическое благополучие.
3. ДЕТЕРМИНАЦИОННЫЙ АНАЛИЗ ВЛИЯНИЯ ФАКТОРОВ СРЕДЫ НА ЭКОЛОГИЧЕСКОЕ СОСТОЯНИЕ БИОТЫ
3.1. Отклики биоценоза рыбоводного пруда на изменение биогенной нагрузки
Исходные данные для детерминационного анализа были взяты из рыбоводных прудов Астраханской области, функционировавших в режиме поликультуры (растительноядные рыбы и карп). За четыре года (1987-1990 гг.) были исследованы 12 прудов (Булгаков и др., 1992). В 4-х из них проводили удобрительный эксперимент, в ходе которого проверяли возможность направленного регулирования состава фитопланктонного сообщества для улучшения кормовой базы растительноядных рыб (главным образом, облигатного фитопланктофага — белого толстолобика). Известно (Савина, 1968; Омаров, Лазарева, 1974), что наиболее предпочтительными в смысле усваиваемости и отсутствия токсического эффекта для питания рыб являются представители зеленых, эвгленовых и диатомовых водорослей. В то же время синезеленые, как правило, избегаются белым толстолобиком из-за их низкой пищевой ценности или даже токсичности. Вместе с тем установлено, что высокие дозы вносимого в водоем минерального азота и высокие отношения азота к фосфору приводят к повышению рыбопродуктивности (Винберг, Ляхнович, 1965). Повышенная азотная нагрузка в удобрениях стимулирует развитие Chlorococcales как излюбленной пищи толстолобиков (Сокольская, 1981; Ивашечкина, 1988; Ульянов, 1988). Таким образом, при помощи ДА предстояло проверить перечисленные гипотезы о существующих в рыбоводном пруду трофических связях в цепи “биогенные элементы — микроводоросли — белый толстолобик”.
Набор переменных, для которых имелись данные по всем прудам, включал следующие блоки:
1) рыбоводные характеристики — продуктивность отдельно по видам рыб и общая рыбопродуктивность;
2) количество внесенных азотных и фосфорных удобрений (сумма за сезон и отдельно за апрель-май, июнь-июль, август-сентябрь);
3) гидрохимические параметры прудов — содержание кислорода, pH, концентрация минеральных форм азота и фосфора, отношение концентраций азота и фосфора;
4) биомассы отделов и порядков фитопланктона (хлорококковые, вольвоксовые, зеленые, диатомовые, синезеленые, эвгленовые) и общая его биомасса;
5) биомассы классов и отрядов зоопланктона (Copepoda, Cladocera, Rotatoria) и общая его биомасса.
Для переменных из блоков 3-5 в виде отдельных переменных использовали среднесезонные значения соответствующего параметра, а также усреднения за апрель-май, июнь-июль, август-сентябрь.
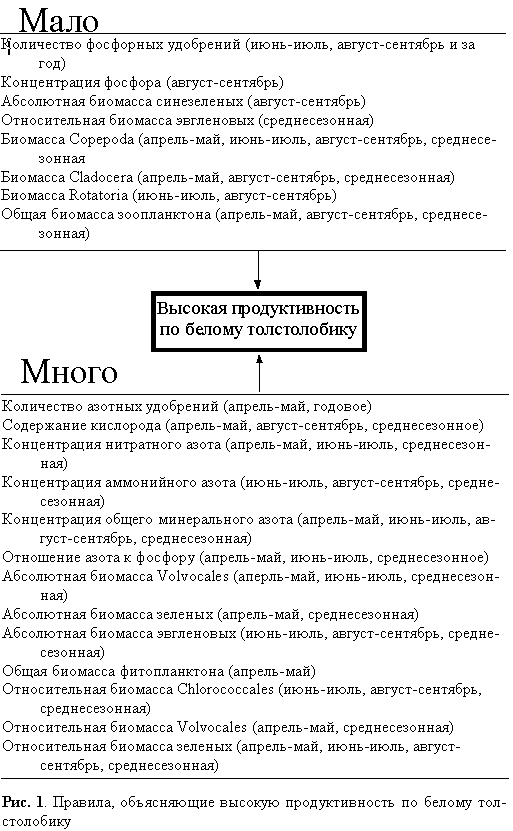
Для подготовки ввода данных в систему ДА весь ряд из 12 значений для каждой переменной был маркирован качественным признаком “мало” или “много”. Разбиение на два указанных класса в каждом случае происходило нелинейным образом так, чтобы в каждом классе оказалось не менее 4 и не более 8 значений. При этом для гидрохимических переменных граница между классами принималась исходя из соответствующих нормативов ПДК. С помощью ДА исследовали сопряженности (правила) между высокой рыбопродуктивностью (то есть в классе “много”) с одной стороны и всем комплексом остальных упомянутых выше переменных — с другой. При этом правилом называется условное суждение, связывающее причину и следствие в изучаемом явлении. Например, “если количество внесенных июне-июле азотных удобрений (объясняющая переменная) соответствовало классу “много”, то значение продуктивности по белому толстолобику (объясняемая переменная) также соответствовало классу “много”. Ценность правила, как было указано выше, задается критериями “точности” и “полноты”. Поясним их смысл в рассматриваемом примере. Для продуктивности по белому толстолобику количество наблюдений в классе “много” равно 5, для количества азотных удобрений — 7. Количество совпавших наблюдений составило 3. Следовательно, из 7 случаев, когда вносилось много азотных удобрений, в 3 случаях значение продуктивности относилось к классу “много”. Тогда Т = 3/7 = 43%. При этом в исследованном массиве данных продуктивность принимала эти значения 5 раз, то есть П = 3/5 = 60%. Для анализа были отобраны не все правила, а лишь те, которые соответствуют определенным порогам точности и полноты (соответственно не менее 50 и 60%).
Сопряженности, определяющие высокую продуктивность по белому толстолобику, практически полностью подтверждают все высказанные предположения о способах повышения экологической эффективности при переходе с нулевого (биогенные элементы) на второй (растительноядные рыбы) трофический уровень (рис. 1). Высокому выходу биомассы толстолобиков соответствует повышенное количество азотных и пониженное — фосфорных; высокая концентрация всех минеральных форм азота и низкая — минерального фосфора и, соответственно, повышенное соотношение N:P в воде; увеличенное содержание растворенного кислорода; повышенная биомасса (абсолютная и относительная) зеленых водорослей и пониженная — синезеленых водорослей. В отношении диатомовых существенных детерминаций не найдено, а эвгленовые присутствуют по относительной биомассе в классе “мало”. Примечательно также, что в тех случаях, когда пруды обладали высокой продуктивностью по белому толстолобику, чаще всего в них было мало зоопланктона (по биомассе), что могло быть обусловлено конкуренцией между двумя группами растительноядных организмов за сходный фитопланктонный ресурс.
Очевидно, что данные детерминационного анализа всего комплекса трофических связей в пруду в целом совпали с представлениями авторов о закономерностях функционирования его экосистемы. Основными предпосылками улучшения “ихтиологического” качества водоема (за счет увеличения плодородия растительноядной составляющей) являются: перераспределение видовой структуры фитопланктона в сторону преобладания Chlorococcales и зеленых в целом и снижения роли синезеленых; достаточная аэрированность воды; высокий фон минерального азота и высокое отношение азота к фосфору в воде, что достигается соответствующим подбором количеств удобрений.
При этом ценность полученных результатов могла бы быть более высокой, если бы мы имели в своем распоряжении не 12 наблюдений, а гораздо больше. Ведь чем больше число случаев совпадений двух независимых событий, тем больше оснований считать эти результаты не слу- чайными. Понятно, что, например, правило “из 50 наблюдений с высоким отношением азота к фосфору 40 совпали с высокой рыбопродуктивностью” более ценнно, чем правило “из 5 наблюдений с высоким отношением азота к фосфору 4 совпали с высокой рыбопродуктивностью”, хотя точности обеих правил одинаковы и равны 80%.
3.2. Гидрохимические индикаторы качества речной воды и их влияние на сообщество зоопланктона.
В работе были использованы данные по гидрохимии, гидрологии (1-й массив) и гидробиологии (численность видов зоопланктона, 2-й массив) на трех участках р. Суры — собственно река, Сурское водохранилище и приплотинный участок водохранилища (Максимов и др., 1999). Пробы отбирали в течение пяти лет (1993-1997) в реке и водохранилище только в летние месяцы (несколько проб в месяц), в приплотинном участке — раз в месяц в течение всего года. Всего было проведено 199 наблюдений.
1-й массив включал числовые значения следующих абиотических переменных: БПК5, концентрации железа, марганца, аммония, нитритов, нитратов, фосфатов, углеводородов, фенолов, растворенного кислорода, взвешенных веществ, а также температуру воды и pH.
Из массива гидробиологических данных были отобраны 11 видов и 3 личиночные стадии зоопланктона, которые встречались не менее, чем в 20% наблюдений: Bosmina coregoni, Bosmina longirostris, Chydorus sphaericus,
 Daphnia cucullata, Daphnia longispina, Epistylis sp., Euchlanis dilatata, Eudiaptomus sp., Eudiaptomus gracilis, Keratella quadrata, Mesocyclops leuckarti, личинки Copepoda, прочие личинки, науплии. Каждая из 14 групп была разделена на два класса: “мало” (низкая численность) и “много” (высокая численность). Нулевые значения численностей не были исключены из анализа, а также включены в класс “мало”, поскольку в действительности значение численности, равное нулю, совсем не обязательно говорит о его отсутствии в пробе. При существующих методиках измерения численности вполне вероятно, что ни один экземпляр вида с низким обилием просто не попадет в поле зрения исследователя. Таким образом, введение качественной переменной в ДА позволяет не задумываться над тем, как относиться к нулевым значениям — действительно ли их приравнивать к нулю или считать пропущенными. В нашем случае, поскольку доля наблюдений с нулевыми численностями практически для всех видов превышала 50%, классы “мало” и “много” сильно отличались по наполненности. Так как в класс “мало” попали, кроме нулевых, значения численности <0.15*103 кл/л, он оказался примерно в 3 раза больше по числу наблюдений, чем класс “много”.
Daphnia cucullata, Daphnia longispina, Epistylis sp., Euchlanis dilatata, Eudiaptomus sp., Eudiaptomus gracilis, Keratella quadrata, Mesocyclops leuckarti, личинки Copepoda, прочие личинки, науплии. Каждая из 14 групп была разделена на два класса: “мало” (низкая численность) и “много” (высокая численность). Нулевые значения численностей не были исключены из анализа, а также включены в класс “мало”, поскольку в действительности значение численности, равное нулю, совсем не обязательно говорит о его отсутствии в пробе. При существующих методиках измерения численности вполне вероятно, что ни один экземпляр вида с низким обилием просто не попадет в поле зрения исследователя. Таким образом, введение качественной переменной в ДА позволяет не задумываться над тем, как относиться к нулевым значениям — действительно ли их приравнивать к нулю или считать пропущенными. В нашем случае, поскольку доля наблюдений с нулевыми численностями практически для всех видов превышала 50%, классы “мало” и “много” сильно отличались по наполненности. Так как в класс “мало” попали, кроме нулевых, значения численности <0.15*103 кл/л, он оказался примерно в 3 раза больше по числу наблюдений, чем класс “много”.
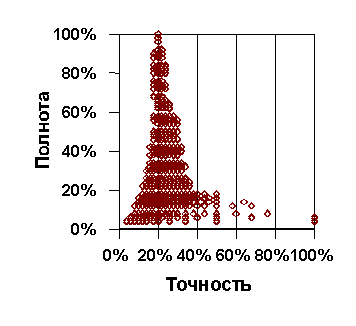
При помощи процедуры оптимизации выясняли, влияют ли колебания гидрохимических и гидрологических показателей на численность отдельных видов. Для оценки такого влияния устанавливали, какой интервал на шкале значений абиотических переменных наиболее достоверно объясняет высокие численности видов. При этом предполагалось, что БПК, концентрация Fe, Mn, углеводородов, фенолов и взвешенных веществ может приводить к снижению численности только в области высоких значений, поэтому при оптимизации задавали верхний уровень искомого интервала. Для содержания кислорода ситуация обратная — только снижение этого показателя может приводить к неблагоприятным последствиям для зоопланктона, поэтому фиксировали нижнюю границу интервала. Что касается концентраций аммония, нитритов, нитратов, фосфатов, температуры и pH, то заранее не накладывали никаких условий на возможные границы, поскольку как слишком высокие, так и слишком низкие значения этих переменных могут вызывать отклонения от благополучного состояния организмов. Так как исследуемые классы объясняемых переменных (высокие численности видов) получились малонаполненными (для большинства видов — 25-30% от общего числа проб), а количество наблюдений в пределах оптимизируемого диапазона абиотических факторов, наоборот, было большим (как правило, более 50%) нельзя было рассчитывать на высокую точность исследуемых правил: как правило, она не превышает 30-40%. Поэтому при оптимизации задавали нижнюю границу полноты (51%), после чего максимизировали точность. С помощью графиков зависимости полноты от точности (рис. 2) легко можно увидеть, на какой максимум точности можно рассчитывать в пределах заданного порога полноты.
Проведенные расчеты (табл. 1) показывают, что из 14 видов и возрастных групп зоопланктона 11 (Bosmina coregoni, Bosmina longirostris, Chydorus sphaericus, Daphnia cucullata, Daphnia longispina, Eudiaptomus sp., Keratella quadrata, Mesocyclops leuckarti, личинки Copepoda, прочие личинки, науплии) демонстрируют, как правило, однородность по отношению к значениям безопасных диапазонов абиотических факторов. Безопасность в данном случае понимается как состояние организма, при котором его численность остается в пределах выбранных нами высоких значений,. Здесь численность отдельных видов и личиночных стадий зоопланктона является индикатором экологического состояния биоценоза, в силу чего полученные диапазоны можно называть экологически допустимымиуровнями (ЭДУ) (Левич, 1994; Maximov et al., 1999) воздействующих на биоценоз факторов. Если же взглянуть на отклики 3-х не попавших в указанную группу видов, то заметно, что по отношению ко многим факторам они более толерантны, то есть ЭДУ этих факторов имеют более широкие границы. Для Epistylis sp. это относится к концентрациям Fe, Mn, O2, аммония (верхний уровень), нитритов (нижний уровень), фенолов, фосфатов (верхний уровень); для Euchlanis dilatata — к БПК, концентрациям Fe, O2, Mn, аммония (верхний уровень), нитритов (верхний уровень), углеводородов, фосфатов (верхний уровень), взвешенных веществ, pH (нижний уровень), температуре (верхний уровень); для Eudiaptomus gracilis — к концентрации нитритов (нижний уровень), нитратов (верхний уровень), pH (нижний уровень), фосфатов (верхний уровень), температуре (нижний уровень). Вместе с тем, по большинству показателей найденные для этих 3-х видов ЭДУ существенно различаются, что, видимо, еще раз говорит об особом положении каждого из них в сообществе зоопланктона. Любопытно сравнить полученные ЭДУ с государственными хозяйственно-питьевыми ПДК, также представленными в табл. 4. По большинству показателей (кроме концентраций марганца, нитритов, нитратов, содержания кислорода) полученные нами границы
Табл. 1. Экологически допустимые уровни факторов среды
|
Вид, возраст- |
ЭДУ |
||||||||||||
|
ная стадия |
БПК, мг/л (в.у.) |
Fe, мг/л (в.у.) |
O2, мг/л (н.у.) |
Mn, мг/л (в.у.) |
NH4, мг/л |
NO2, мг/л |
NO3, мг/л |
УВ, мг/л (в.у.) |
pH |
Фенолы, мг/л (в.у.) |
PO4-, мг/л |
t, 0C |
ВВ, мг/л (в.у.) |
|
Bosmina coregoni |
2.6 |
0.72 |
8 |
0.09 |
0.2-0.555 |
0.034-0.08 |
0.02-0.52 |
0.034 |
8.07-9.5 |
0.0058 |
0-0.24 |
21-27 |
11.5 |
|
Bosmina longirostris |
3.9 |
0.48 |
8.4 |
0.07 |
0.2-0.76 |
0.046-0.36 |
0.02-0.68 |
0.52 |
7.93-9.56 |
0.004 |
0.15-1.14 |
19-30 |
20.5 |
|
Chydorus sphaericus |
5.04 |
0.8 |
6 |
0.06 |
0.13-0.65 |
0.035-0.13 |
0.02-0.49 |
0.122 |
8-9.2 |
0.003 |
0-0.12 |
22-27 |
22.5 |
|
Daphnia cucullata |
2.6 |
0.64 |
8.4 |
0.04 |
0.2-0.555 |
0.036-0.08 |
0.07-0.68 |
0.35 |
8.05-9.45 |
0.0071 |
0.19-1.14 |
21-27 |
11 |
|
Daphnia longispina |
4.56 |
0.84 |
7.7 |
0.06 |
0.2-0.75 |
0.042-0.124 |
0.3-0.87 |
0.034 |
8.12-9.5 |
0.009 |
0-0.095 |
20-25 |
12 |
|
Eudiaptomus sp. |
12.16 |
0.84 |
8.4 |
0.09 |
0.2-0.66 |
0.042-0.124 |
0.36-0.97 |
0.036 |
8.2-9.45 |
0.0071 |
0.06-0.26 |
21-25 |
11 |
|
Keratella quadrata |
7.04 |
0.43 |
7.7 |
0.05 |
0.2-0.555 |
0.029-0.08 |
0.02-0.76 |
0.093 |
7.76-9.45 |
0.004 |
0.06-0.26 |
20-26 |
6.5 |
|
Mesocyclops leuckarti |
4.32 |
1.32 |
8.56 |
0.06 |
0.4-2.9 |
0.042-0.13 |
0.16-0.84 |
0.037 |
7.98-9.45 |
0.016 |
0-0.12 |
19-25 |
14 |
|
Larvae |
2.56 |
0.84 |
8.4 |
0.04 |
0.2-0.555 |
0.042-0.196 |
0.27-0.97 |
0.037 |
8.07-9.45 |
0.009 |
0.06-0.26 |
19-25 |
5.8 |
|
Larvae Copepoda |
4.8 |
0.87 |
8.08 |
0.07 |
0.6-2.4 |
0.035-0.16 |
0.02-1.03 |
0.52 |
7.7-9.56 |
0.0071 |
0-0.22 |
20-30 |
19 |
|
Nauplii |
3.9 |
0.69 |
8.16 |
0.06 |
0.2-0.93 |
0.044-0.36 |
0.02-0.68 |
0.066 |
7.76-9.56 |
0.016 |
0.06-0.26 |
19-26 |
16.5 |
|
Epistylis sp. |
3.2 |
1.21 |
4.9 |
0.14 |
0.508-0.97 |
0.025-0.057 |
0.52-1.04 |
0.053 |
8.07-9.5 |
0.009 |
0.14-0.6 |
20.5-23 |
9.6 |
|
Euchlanis dilatata |
7.44 |
1.5 |
4.8 |
0.42 |
0.83-2.2 |
0.05-0.89 |
0.12-0.65 |
0.69 |
6.5-7.8 |
0.0028 |
0.21-2.4 |
20-30 |
26 |
|
Eudiaptomus gracilis |
1.92 |
0.34 |
7.7 |
0.05 |
0.24-0.84 |
0-0.064 |
0.76-6.5 |
0.053 |
7.5-8.36 |
0.0037 |
0-0.1.94 |
0-20.5 |
5 |
|
ПДК |
3 |
0.3 |
4 |
0.1 |
0.5 |
3.3 |
45 |
6.5-8.5 |
0.001 |
0.25 |
|||
оказываются шире стандартных нормативов. Так что можно утверждать, что зоопланктонное сообщество р. Суры достаточно устойчиво к действию внешних факторов, а определенные в лабораторных условиях ПДК не вполне отражают его адаптационный потенциал.
Причины исключительного положения трех отмеченных видов вероятно кроются в их особом экологическом статусе. Так, известно, что E. dilatata и E. gracilis представляют собой эврибионтные виды, легко приспосабливающиеся к обитанию в самых широких пределах факторов среды. Отсюда и их пределы толерантности, по большинству показателей самые широкие среди всех видов.
4. ЗАКЛЮЧЕНИЕ
Полученные результаты показали, что детерминационный анализ может быть достаточно эффективным средством нахождения связей между различными компонентами экосистемы, в частности, для поиска и вычисления значений факторов, влияющих на биотические индикаторы качества природных экосистем. Дальнейшие перспективы применения метода связаны с исследованием интегральных характеристик экосистемы, таких как обобщенный класс качества вод по абиотическим показателям, индекс сапробности сообществ гидробионтов. Возможно более широкое использование многофакторного подхода (когда в качестве объясняющей переменной в анализе участвуют одновременно несколько факторов), например, при анализе связей между биотической и абиотической частями экосистемы. С помощью процедуры ДА, называемой введением контекста, можно изучать любые связи в пределах любого выделенного фрагмента из общего массива данных (например, при исследовании одного гидрографического района проводить анализ отдельно для составляющих его крупных рек).
Следует отметить, что научные задачи, к которым приложим предлагаемый подход, крайне актуальны. В частности, требует новых методических подходов задача анализа взаимосвязей факторов в сложных многофакторных системах. Задача поиска причин экологического неблагополучия приобретает особо важное значение в связи с неудовлетворительным обоснованием существующих систем экологического контроля (Maximov et al., 1999). С помощью ДА облегчается задача поиска региональных ЭДУ факторов среды, несущих потенциальную опасность для различных биотических компонентов экосистем.
Литература
Будилова Е.В., Дрогалина Ж.А., Терехин А.Т. Основные направления современной экологии и ее математический аппарат: анализ публикаций // Журнал общей биологии. 1995. Т.56. №2. С.179-190.
Булгаков Н.Г., Левич А.П., Никонова Р.С., Саломатина Т.В. О связи между экологическими параметрами и продукционными показателями выростного рыбоводного пруда // Вестник МГУ. Сер. биол. 1992. №2. С.57-62.
Винберг Г.Г., Ляхнович В.П. Удобрение прудов. М., 1965.
Замолодчиков Д.Г., Булгаков Н.Г., Гурский А.Г., Левич А.П., Чесноков С.В. К методике применения детерминационного анализа для обработки экологических данных // Биол. науки. 1992. №7. С.116-133.
Ивашечкина Н.Б. Фитопланктон и его продукция в прудах саратовского рыбопитомника // Сб. науч. тр. ГосНИОРХ. 1988. 277. С.14-27.
Левич А.П. Биотическая концепция контроля природной среды // Доклады РАН. 1994. Т.337. №2. С.280.
Левич А.П., Терехин А.Т. Метод расчета экологически допустимых уровней воздействия на экосистемы // Водные ресурсы. 1997. №3. С.328-335.
Левич А.П., Булгаков Н.Г., Замолодчиков Д.Г. Оптимизация структуры кормовых фитопланктонных сообществ. Под ред. проф. В.Н.Максимова. М.: Товарищество научных изданий КМК. 1996. 136 с.
Максимов В.Н., Левич А.П., Булгаков Н.Г., Милованова Г.Ф. Детерминационный анализ связей в биотическом и абиотическом компонентах экосистемы и между этими компонентами // Известия РАН. Сер. биол. 1999 (в печати).
Налимов В.В., Чернова В.А. Статистические методы планирования экстремальных экспериментов. М.: Наука, 1965. 340 с.
Омаров М.О., Лазарева Л.П. Питание белого толстолобика в водоемах Дагестана // Гидробиол. ж. 1974. 10. №4. С.100-104.
Савина Р.А. Питание белого толстолобика Hypophthalmichthys molitrix Val. в прудах. Автореф. канд. дис. Рыбное, 1968.
Сокольская Н.И. Формирование биопродуктивности водоемов дельты Волги и пути использования ее закономерностей. Автореф. канд. дис. М., 1981.
Ульянов В.Н. Влияние минеральных удобрений на развитие естественной кормовой базы прудов // Сб. науч. тр. ГосНИОРХ. 1988. 288. С.113-115.
Хейс Д. Причинный анализ в статистических исследованиях. М.: Финансы и статистика, 1980. 255 с.
Azzi G. Agricultural Ecology. Turin, 1928. 237 pp. Digby P.G.N., Kempton R.A. Multivariate Analysis of
Maximov V.N., Bulgakov N.G., Levich A.P. Quantitative methods of ecological control: diagnostics, standardization, and prediction // Environmental indices: Systems analysis approach. London: EOLSS Publishers, 1999. Pp.363-381