 ,
, Энтропийный экстремальный принцип в экологии сообществ: результаты и обсуждение
Левич А.П., Алексеев В.Л.
Согласно предложенному энтропийному экстремальному принципу в реальности осуществляются состояния биологической системы, на которых достигается экстремум функционала, имеющего смысл меры структурированности системы. В частности, показано, что наличные ресурсы среды однозначно определяют состояние сообщества согласно полученной формуле видовой структуры. Сформулировано правило лимитирующего звена согласно которому для любой комбинации ресурсов в пространстве потребляемых ресурсов среды существуют области, в которых состояние сообщества полностью определяется только этой комбинацией. В частности, существуют области, где определяющим является любой фиксированный ресурсный фактор, любые два или несколько факторов сразу. Т.о. правило лимитирующего звена обобщает классические концепции лимитирования Либиха и Митчерлиха. Доказано, что с математической точки зрения рассматриваемый экстремальный принцип эквивалентен принципу минимального потребления, требующему минимизации потребления ресурса среды при ограничении на степень структурированности системы. Рассмотрен вариант энтропийного экстремального принципа, позволяющий рассчитывать траектории системы, как функции от потребленных ресурсов.
При описании функционирования биологических систем в теоретической биологии широко используется понятие экстремальности: принимается гипотеза, в силу которой из всего возможного спектра состояний биологической системы осуществляется то, для которого экстремальна некоторая заранее выбранная характеристика системы [1]. Например, в экологии в качестве такой характеристики используется показатель экспансии размножения популяций — тотальная биомасса [2], продуктивность [3] или удельная скорость роста [4]. В работах одного из авторов [5,6] на основании теоретико-категорных методов сравнения математических структур, был выдвинут энтропийный экстремальный принцип, который использовался затем в серии работ. В настоящей работе мы хотели бы привести некоторые результаты, полученные в последнее время при использовании этого принципа.
Энтропийный экстремальный принцип
Коротко напомним суть энтропийного экстремального принципа. Экологическое сообщество моделируется с помощью множеств с разбиениями [5,6]. Элементы множеств — это особи, классы разбиения — популяции биологических видов. Переходы сообщества из одних состояний в другие описываются соответствиями между множествами с разбиениями. Обычно из постановки задачи ясно, какие допускаются соответствия. Например, если мы хотим описать смертность особей, то допускаются не всюду определенные соответствия между множествами с разбиениями; если мы описываем размножение особей, то рассматриваются многозначные (нефункциональные соответствия) и т.д. С каждым состоянием сообщества, т.е. с соответствующим множеством с разбиением A, мы свяжем следующую величину, называемую энтропией состояния A:
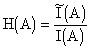 ,
,
где ![]() — общее количество допустимых соответствий из A в A, а I(A) — количество допустимых соответствий из A в A, с дополнительным требованием: соответствие должно переводить каждый класс разбиения A целиком в другой класс разбиения и разные классы разбиения переводить в разные. Постулируется следующий экстремальный принцип: в реальности осуществляется состояние A для которого величина H(A) максимальна при ограничениях, накладываемых конечностью ресурсов среды. Мотивы, побудившие к подобной формулировке, основаны на теоретико-категорных методах сравнения математических структур. Они подробно изложены в книге одного из авторов [6] в главах, специально посвященных методу функторного сравнения структур, обобщающему сравнение множеств с помощью кардинальных чисел.
— общее количество допустимых соответствий из A в A, а I(A) — количество допустимых соответствий из A в A, с дополнительным требованием: соответствие должно переводить каждый класс разбиения A целиком в другой класс разбиения и разные классы разбиения переводить в разные. Постулируется следующий экстремальный принцип: в реальности осуществляется состояние A для которого величина H(A) максимальна при ограничениях, накладываемых конечностью ресурсов среды. Мотивы, побудившие к подобной формулировке, основаны на теоретико-категорных методах сравнения математических структур. Они подробно изложены в книге одного из авторов [6] в главах, специально посвященных методу функторного сравнения структур, обобщающему сравнение множеств с помощью кардинальных чисел.
Приведем здесь лишь некоторые из возможных интерпретаций экстремального принципа.
1) Разбиение множества A можно рассматривать как введение на Ф некоторой структуры и тогда энтропия H(A) интерпретируется как мера удаленности структурированного состояния A от своего аналога со “стертой” структурой. Согласно экстремальному принципу осуществляются состояния, которые сильнее других удалены от своего полностью бесструктурного прообраза.
2) Величина ![]() зависит лишь от мощности множества A (от полной численности сообщества) и поэтому если полная численность сообщества фиксирована, то величина H(A) максимальна, если знаменатель, т.е. число всех сохраняющих структуру сообщества преобразований, минимален. Малый набор допустимых структурой системы преобразований можно трактовать как высокую устойчивость состояния. И экстремальный принцип реализует максимально устойчивое состояние сообщества.
зависит лишь от мощности множества A (от полной численности сообщества) и поэтому если полная численность сообщества фиксирована, то величина H(A) максимальна, если знаменатель, т.е. число всех сохраняющих структуру сообщества преобразований, минимален. Малый набор допустимых структурой системы преобразований можно трактовать как высокую устойчивость состояния. И экстремальный принцип реализует максимально устойчивое состояние сообщества.
3) Как показано одним из авторов [5], при определенном выборе допустимых соответствий между множествами с разбиениями функционалы H(A) совпадают с так называемыми императивными индексами разнообразия, используемыми в экологии. С этой точки зрения экстремальный принцип означает, что осуществляется состояние сообщества с максимальным разнообразием (см. также [7]).
4) Энтропию системы можно рассматривать как количество информации, связанной со структурой системы [8], поэтому введенный экстремальный принцип можно интерпретировать и в информационных терминах.
В дальнейшем изложении будут обоснованы еще две интерпретации энтропийного принципа: принцип минимального потребления и энтропийная параметризация собственного времени системы.
Рассмотрим теперь сообщество, состоящее из организмов одного трофического уровня без возрастной структуры (например, из клеток фитопланктона), принадлежащих w видам и потребляющих m взаимонезаменимых ресурсов. Пусть в рассматриваемом сообществе допустимы деление клеток и их гибель, но недопустимы поглощение одних организмов другими и интродукция особей извне. Таким требованиям удовлетворяют инъективные, сюръективные, не всюду определенные и не функциональные соответствия. Энтропийный функционал для такого сообщества приобретает вид [6]:
![]()
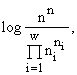 (1)
(1)
Вариационная задача включает ресурсные ограничения, которые имеют вид
![]() (2)
(2)
Здесь ![]() — наличное количество в среде k-го ресурса, а q — потребность особи вида i в k-том ресурсе (всего рассматривается w видов и m ресурсов; мы считаем, что w > 1 и
— наличное количество в среде k-го ресурса, а q — потребность особи вида i в k-том ресурсе (всего рассматривается w видов и m ресурсов; мы считаем, что w > 1 и ![]() > 0). В (2) мы используем знак неравенства (в отличие от знака равенства в нашей предыдущей работе [9]), поскольку ниоткуда не следует, что все k ресурсов будут потреблены полностью, т.е. перейдут из среды внутрь особей, а указать, какие именно ресурсы будут потреблены полностью, мы заранее не можем. Поэтому в (2) более реалистично использовать знак неравенства. Таким образом, мы решаем экстремальную задачу
> 0). В (2) мы используем знак неравенства (в отличие от знака равенства в нашей предыдущей работе [9]), поскольку ниоткуда не следует, что все k ресурсов будут потреблены полностью, т.е. перейдут из среды внутрь особей, а указать, какие именно ресурсы будут потреблены полностью, мы заранее не можем. Поэтому в (2) более реалистично использовать знак неравенства. Таким образом, мы решаем экстремальную задачу
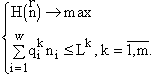 (3)
(3)
Решение задачи (3) методом Лагранжа приводит к формуле видовой структуры [5,10]
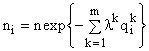 , (4)
, (4)
связывающей численности видов в сообществе с ресурсами ![]() , от которых в формуле зависят n и
, от которых в формуле зависят n и ![]() . Они являются решениями следующей системы равенств и неравенств
. Они являются решениями следующей системы равенств и неравенств
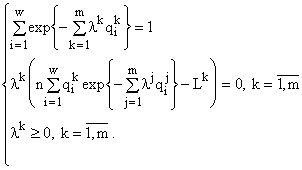 (5)
(5)
В работах [11,12] адекватность формулы видовой структуры установлена в опытах с лабораторными альгоценозами из 4, 8, и 10 видов, культивировавшихся на двух десятках сред с различными комбинациями начальных концентраций азота и фосфора в питательных средах.
Некоторые следствия энтропийного экстремального принципа
1) Вектор ресурсов ![]() определяет состояние сообщества однозначно [10]. Это значит, что решение (3) существует и единственно (оно даётся формулой (4)) для всех допустимых
определяет состояние сообщества однозначно [10]. Это значит, что решение (3) существует и единственно (оно даётся формулой (4)) для всех допустимых ![]() . В (3) допустимы любые
. В (3) допустимы любые ![]() , у которых
, у которых ![]() (это прямо следует из смысла
(это прямо следует из смысла ![]() при постановке задачи).
при постановке задачи).
2) Из формулы (4) мы видим, что ![]() т.е. конкурентное исключение отсутствует. В связи с этим заметим, что если вместо задачи (3) с функционалом
т.е. конкурентное исключение отсутствует. В связи с этим заметим, что если вместо задачи (3) с функционалом ![]() рассматривать задачу
рассматривать задачу
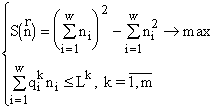
с функционалом ![]() , связанным с симпсоновским индексом разнообразия сообщества [5], то мы получим, что максимум достигается, когда некоторые из численностей
, связанным с симпсоновским индексом разнообразия сообщества [5], то мы получим, что максимум достигается, когда некоторые из численностей ![]() , т.е. получим возможность конкурентного исключения. Отметим, что функционал
, т.е. получим возможность конкурентного исключения. Отметим, что функционал ![]() появляется в нашей модели, если мы считаем допустимыми произвольные соответствия между множествами с разбиениями, т.е. помимо деления клеток и их гибели мы допускаем поглощение одних организмов другими и интродукцию особей извне.
появляется в нашей модели, если мы считаем допустимыми произвольные соответствия между множествами с разбиениями, т.е. помимо деления клеток и их гибели мы допускаем поглощение одних организмов другими и интродукцию особей извне.
3) Так как вектор ресурсов ![]() определяет состояние сообщества однозначно,то меняя его можно управлять структурой сообщества. В связи с этим интересно рассмотреть вопрос, при каких
определяет состояние сообщества однозначно,то меняя его можно управлять структурой сообщества. В связи с этим интересно рассмотреть вопрос, при каких ![]() относительная численность некоторого заранее выбранного вида с номером i принимает наибольшее значение из всех возможных в полном диапазоне изменений вектора
относительная численность некоторого заранее выбранного вида с номером i принимает наибольшее значение из всех возможных в полном диапазоне изменений вектора ![]() .
.
Пусть m = 1. Тогда из первого уравнения (5) мы находим, что множитель ![]() не зависит от
не зависит от ![]() . Следовательно, относительная численность i-го вида
. Следовательно, относительная численность i-го вида ![]() не зависит от
не зависит от ![]() и наш вопрос теряет содержательность.
и наш вопрос теряет содержательность.
Разберем подробно случай m = 2, который наиболее часто встречается в эксперименте и доказательство для которого содержит все идеи общей ситуации, будучи свободно от техническмх трудностей последней (теорема о максимуме видовых обилий).
Введем обозначения ![]() и
и ![]() . Тогда (5) запишется в виде
. Тогда (5) запишется в виде
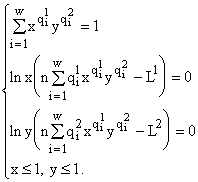 (6)
(6)
Из первого уравнения (6) мы можем найти y как функцию от x. Примерный график y(x) представлен на рис.1. Из него видно, что для выполнения условий ![]() , нужно, чтобы
, нужно, чтобы ![]() , где
, где ![]() — единственный корень
— единственный корень ![]() . Для
. Для ![]()
![]() и
и ![]() отличны от нуля, и тогда, деля второе уравнение (6) на третье и обозначив
отличны от нуля, и тогда, деля второе уравнение (6) на третье и обозначив ![]() как t, мы получаем отображение t = t(x) интервала
как t, мы получаем отображение t = t(x) интервала ![]() на некоторый интервал
на некоторый интервал ![]() оси t:
оси t:
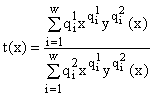 ,
,
где y(x) находится из первого уравнения (6). Используя при вычислении dt/dx теорему о неявной функции, можно показать, что dt/dx > 0, т.е. t(x) строго монотонно возрастающая функция. Поэтому мы имеем
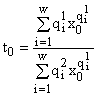 и
и 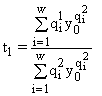 ,
,
где ![]() — единственный корень
— единственный корень ![]() и для любого
и для любого ![]() уравнение
уравнение ![]() имеет единственное решение
имеет единственное решение ![]() . По этому x мы находим y(x), причем получаем x < 1 и y < 1, а затем находим n.
. По этому x мы находим y(x), причем получаем x < 1 и y < 1, а затем находим n.
Таким образом, мы видим, что если вектор ![]() таков, что
таков, что 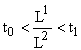 , то для вида i относительная численность
, то для вида i относительная численность ![]() есть функция от
есть функция от ![]() , причем
, причем
![]() ,
,
т.е. если 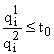 , то
, то ![]() на
на ![]() имеет максимум при t =
имеет максимум при t =![]() , если
, если 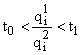 , то при
, то при ![]() , а если
, а если 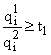 , то при t =
, то при t =![]() .
.
Пусть теперь вектор ![]() таков, что
таков, что 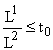 . Тогда в (6) надо положить x = x0, y = 1 и
. Тогда в (6) надо положить x = x0, y = 1 и ![]() , а если
, а если 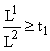 , то надо положить x = 1, y = y0 и
, то надо положить x = 1, y = y0 и ![]() . То, что эти решения единственны, показано в работе [9].
. То, что эти решения единственны, показано в работе [9].
В итоге мы получаем, что относительные численности зависят лишь от отношения ![]() и для вида i достигают своего максимума при
и для вида i достигают своего максимума при  . Типичная картина поведения относительных численностей
. Типичная картина поведения относительных численностей ![]() как функций от t =
как функций от t =![]() представлена на рис.2.
представлена на рис.2.
Этот вывод остается справедливым и в общем случае: относительная численность заданного вида принимает наибольшее значение при отношениях в среде ресурсных факторов, равных отношениям потребностей в них данного вида.
Обзор многих экспериментальных фактов, согласующихся с этим выводом можно найти в работах [9,13,14,15,16].
4) Для задачи с неравенствами (3) доказано [10] правило лимитирующего звена, обобщающее принцип минимума Либиха и закон совокупного действия факторов Митчерлиха (подробности см., например, в [17]). Согласно этому правилу (теорема стратификации) пространство потребляемых ресурсных факторов среды распадается (стратифицируется) на ![]() непересекающихся подмножеств, каждому из которых соответствует единственный набор потребляемых ресурсных факторов, которые (и только они) в этом подмножестве:
непересекающихся подмножеств, каждому из которых соответствует единственный набор потребляемых ресурсных факторов, которые (и только они) в этом подмножестве:
а) потребляются полностью;
б) являются аргументами экстремали (4) (т.е. ni, ![]() являются функциями лишь от этих факторов).
являются функциями лишь от этих факторов).
Таким образом, мы можем сказать, что состояние сообщества ![]() зависит от тех и только тех ресурсных факторов, которые потребляются полностью.
зависит от тех и только тех ресурсных факторов, которые потребляются полностью.
Энтропийный экстремальный принцип и “теорема Гиббса”
Сделаем еще одно пояснение о смысле энтропийного экстремального принципа. Имеет место следующая теорема:
Пусть ресурсный фактор единственен и пусть l — единственный корень уравнения ![]() Тогда эквивалентны следующие две задачи:
Тогда эквивалентны следующие две задачи:
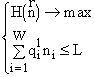 и
и 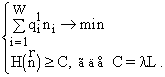
Эту теорему мы назвали “теоремой Гиббса”, т.к. в термодинамике аналогичное утверждение об эквивалентности задачи на максимум энтропии при фиксированном уровне энергии задаче на минимум энергии при фиксированном уровне энтропии доказал Гиббс [18].
Т.о. мы видим, что смысл энтропийного экстремального принципа достаточно прозрачен: требуется минимальность потребления ресурсного фактора при ограничении снизу на некоторую характеристику биосистемы, которую можно трактовать как ее сложность или разнообразие.
В случае m ³
2 возможно следующее обобщение “теоремы Гиббса”. Пусть мы имеем вектор ![]() , соответствующий решению (4) задачи (3), и пусть
, соответствующий решению (4) задачи (3), и пусть ![]() Рассмотрим следующую экстремальную задачу:
Рассмотрим следующую экстремальную задачу:
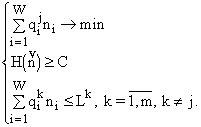 (7)
(7)
Тогда можно показать, что решение (4) задачи (3) является одновременно решением системы (7).
Верно и обратное утверждение: если ![]() — решение системы (7), то
— решение системы (7), то ![]() будет решением и задачи (3) с
будет решением и задачи (3) с ![]()
Экстремальный принцип, отраженный задачей (7), мы назовем принципом минимального потребления для любого из ресурсных факторов.
“Динамический” вариант энтропийного экстремального принципа
В естествознании экстремальные принципы традиционно применяются для получения уравнений движения. Достаточно упомянуть Лагранжев подход к механике, при котором уравнение траектории движения есть уравнение экстремали некоторого функционала (лагранжиана).
Как можно модифицировать энтропийный экстремальный принцип, чтобы получить какой-либо аналог траектории? Предлагается следующий принцип: из начального состояния ![]() в реальности осуществляется переход в состояние
в реальности осуществляется переход в состояние ![]() , которое в рамках прежней теоретико-категорной модели экологии сообществ служит решением следующей экстремальной задачи:
, которое в рамках прежней теоретико-категорной модели экологии сообществ служит решением следующей экстремальной задачи:
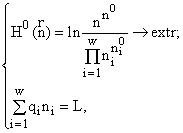 (8)
(8)
где ![]()
Легко видеть, что если ![]() , то мы приходим к задаче (3), в которой m = 1, ибо при этом
, то мы приходим к задаче (3), в которой m = 1, ибо при этом ![]() (см.(1)), а при m = 1 в (3) неравенство можно заменить на равенство (это следует из (5)). Т.о. введенный принцип служит естественным обобщением энтропийного экстремального принципа. В результате решения задачи (8) мы получаем траекторию
(см.(1)), а при m = 1 в (3) неравенство можно заменить на равенство (это следует из (5)). Т.о. введенный принцип служит естественным обобщением энтропийного экстремального принципа. В результате решения задачи (8) мы получаем траекторию ![]() (L) где количество потребленного ресурса L играет роль параметра движения, т.е. является аналогом времени. Можно назвать L метаболическим временем [19], а сам введенный принцип рассматривать как “динамический” вариант энтропийного экстремального принципа. При этом энтропийный функционал приобретает интерпретацию энтропийной параметризации собственного времени систем [20].
(L) где количество потребленного ресурса L играет роль параметра движения, т.е. является аналогом времени. Можно назвать L метаболическим временем [19], а сам введенный принцип рассматривать как “динамический” вариант энтропийного экстремального принципа. При этом энтропийный функционал приобретает интерпретацию энтропийной параметризации собственного времени систем [20].
Анализ (8) показывает, что
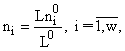 (9)
(9)
где ![]() дает локальный минимум в (8). Таким образом, в метаболическом времени L численности
дает локальный минимум в (8). Таким образом, в метаболическом времени L численности ![]() линейно растут.
линейно растут.
В многочисленных экспериментах с накопительными культурами фитопланктона установлено [21], что процесс роста численности клеточных популяций, обусловленный потреблением биогенного субстрата, закономеро складывается из трех стадий (рис.3):
Стадия A: Накапливание в клетках биогена без увеличения численности клеток.
Стадия B: Деление клеток за счет потребления вещества из среды.
Стадия C: Деление клеток за счет внутренних запасов питательного вещества.
Стадии могут быть редуцированными и перекрывающимися, но они имеют место как для всего сообщества в целом, так и для отдельных видов, входящих в его состав. Отметим, что стадии процесса рост-потребление лишь частично совпадают с фазами роста выявленными по кривым роста n = n(t). А именно, стадия A есть заключительная часть лаг-фазы (на начальной части лаг-фазы нет ни роста культуры ни потребления вещества), а стадии B и C входят в фазу экспоненциального роста.
Таким образом, мы видим, что на стадии B зависимость численности от потребленного субстрата линейна, т.е. аналогична (9). В этом случае ![]() из (8), (9) имеют смысл “квот деления” [22,23].
из (8), (9) имеют смысл “квот деления” [22,23].
Мы надеемся посвятить одну из следующих работ более подробному анализу “динамического” энтропийного экстремального принципа.
Список литературы