Труды семинара "Время, хаос и математические проблемы". М.: Ин-т математических исследований сложных систем МГУ им. М.В.Ломоносова. 2000. Вып. 2.
© А.П.Левич

Энтропия как мера структурированности

сложных систем*

А.П.Левич

Кафедра общей экологии Биологического факультета МГУ им. М.В.Ломоносова

Москва, 119899, Воробьевы горы. Тел. (095) 939-55-60;

e-mail: . Web:

www.chronos.msu.ru

Введение

Представления об энтропии многолики и вездесущи в современной науке.

Определения энтропии. Энтропия термодинамической системы (где Q — полученная системой от среды теплота, а T — температура процесса) была введена в 1865 г. Рудольфом Юлиусом Клаузиусом (Clausius, 1865). В 1872 г. Людвиг Больцман (Boltzmann, 1872) вводит статистическую энтропию S=k lnW (здесь W — вероятность макросостояния, отождествляемая с числом микросостояний системы при условии их равновероятности, а k — коэффициент пропорциональности, зависящий от принятой размерности энтропии.). Джозайя Виллард Гиббс для статистического обоснования термодинамики использует (Gibbs, 1902) вероятностные представления:

(здесь ρ(p,q) — плотность вероятности распределения обобщенных координат q и импульсов p в фазовом пространстве системы, k — размерный множитель). В 1948 г. Клод Шеннон (Shannon, 1948) предложил формулу для оценки неопределенности кодовой информации в каналах связи, называемую энтропией Шеннона: , где pi — вероятность встречаемости символа i в коде, содержащем N символов, k — размерный множитель. В 1953 г. появляется работа Александра Яковлевича Хинчина (1953), где формула Шеннона аксиоматически применяется для описания неопределенности схем в теории вероятности. В работах Роберта Мак Артура (McArthur, 1955) аналог формулы Шеннона появился как мера биологического разнообразия экологических сообществ: , здесь ni —численность i-той популяции в сообществе из W видов, . Андрей Николаевич Колмогоров с коллегами (1956) развили вероятностное определение энтропии для приложения к теории информации (f(x) здесь функция распределения случайной величины x). В 1958 г. А.Н.Колмогоров ввел для динамических систем метрическую энтропию, или K-энтропию, которая пропорциональна скорости изменения статистической энтропии Больцмана. (Хайтун, 1996, с.53). До настоящего момента продолжают появляться обобщения энтропийных формул. Так, в 1970 г. Анри Реньи предложил меру 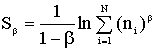, совпадающую при значении параметра β=1 c энтропией Шеннона (Климонтович, 1995, с.11). Александр Владимирович Коганов обобщил статистическое определение комбинаторной энтропии – логарифм числа состояний системы – на понятие математической модели (Коганов, 2000).

Применение энтропии. Не менее разнообразны и примеры применения понятия энтропии. Идеология всех таких приложений связана с экстремальными принципами естествознания – возрастающее значение энтропии параметризует изменение состояния систем самой различной природы в процессе их “естественной” эволюции. Соответствующий принцип развития получил название “принцип максимума энтропии”. Для закрытых термодинамических систем их энтропия возрастает (“второе начало” термодинамики). Распространение “второго начала” на Вселенную (Franklin, 1910; Lotka, 1922; Eddington, 1958) и все процессы в ней привело к представлению об энтропийной “стреле времени”. Принцип максимума энтропии применяется, в частности, в физике (Jaynes, 1957; Tribus, 1961), лингвистике (Мандельброт, 1973), экологии (Приц, 1974; Lurie, Wagensberg, 1982), математике (Gzyl, 1995), механике (Хазен, 1998), экономике и науке о коммуникациях (Wilson, 1970).

Постановка проблемы. В связи с понятием энтропии и его применением возникают научные проблемы, решению некоторых из которых посвящена настоящая работа:

Конструкция энтропии

Путь, на котором я буду пытаться ответить на поставленные вопросы, может быть следующим:

Система как структурированное множество. Обычный (и, возможно, единственный) путь формального описания системы – подбор для неё математической структуры, удачно эксплицирующей содержательные характеристики системы.

Так, экологическое сообщество из особей различных видов удобно описывать структурой множеств с разбиениями, где классы разбиения соответствуют слагающим сообщество популяциям, а элементы множества – организмам.

Множеством с разбиением можно описать распределение частиц газа по энергиям или распределение словоформ в заданном тексте.

Социальная или таксономическая иерархия могут быть представлены как теоретико-множественная совокупность булеанов с отношением включения подмножеств или иным отношением порядка.

Понятие близости-удалённости точек в нашем эмпирическом или априорном представлении о пространстве описывается топологической математической структурой.

Совокупность состояний атома можно описать структурой гильбертова пространства или равносильным образом – полем бесконечных матриц.

Категории вместо множеств. В математике предложен язык для описания произвольных структурированных множеств – теория категорий и функторов. Первая существенная черта теории категорий – рассмотрение не отдельного множества, с какой либо структурой, а включение в поле зрения одновременно всех одинаково структурированных множеств.

Например, совокупность всех множеств с разбиениями или всех множеств, для пар элементов которых задана метрика или закон композиции и т.п.

Совокупность всех одинаково структурированных множеств (другими словами, множеств вместе с заданной на них аксиоматикой) составляет класс объектов категории.

Другая существеннейшая черта теории категорий – явное включение не только самих её объектов, но и всех преобразований, допустимых структурой объектов. Т.е. таких соответствий из одних структурированных множеств в другие структурированные множества, которые не нарушают их структуру.

Например, для множеств с заданным отношением порядка допустимыми будут монотонные соответствия, для множеств с заданной структурой “близости” элементов – топологией – допустимы непрерывные преобразования, переводящие “близкие” элементы в “близкие” же и т.п.

Совокупность допустимых преобразований (на языке теории категорий — морфизмов) задана в категории для каждой пары объектов. При этом категории с совпадающими объектами, но различающимися морфизмами, строго говоря, различны и описывают различающиеся системы. Например, систему, для преобразования состояний которой допустимы произвольные соответствия, мы будем отличать от системы, где те же множества преобразуются лишь взаимно однозначно. Процессы, происходящие в первой системе, богаче, чем во второй — в ней допустимы переходы между состояниями с переменным числом элементов, в то время как во второй системе число элементов в разных состояниях одинаково. Для морфизмов, как и для их прообразов – отображений, – определено “умножение”, совпадающее с композицией функций – последовательным их осуществлением.

Предлагается описывать системы категориями, т.е. система — это некоторая категория, объединяющая класс объектов и класс морфизмов. Аксиоматика математической структуры, определяющая категорию, выделяет заданную систему среди других систем. Объекты категории эксплицируют состояние систем, морфизмы – допустимые способы перехода от одних состояний к другим. Замечу, что теоретико-категорное описание систем не требует обязательной экспликации естественной системы математической структурой. Возможно “качественное” категорное описание систем, т.е. непосредственное перечисление и описание состояний системы и всех переходов между состояниями (морфизмов) не на математическом, а на внутридисциплинарном, содержательном языке.

Последовательное изложение языка теории множеств и теории категорий содержится в книге, специально посвящённой их приложениям к теории систем (Левич, 1982). Там же строго доказаны все утверждения, на которые опирается дальнейшее изложение.

Мощности вместо количеств. Есть два способа сравнить количество элементов в множествах. Пусть нам, к примеру, необходимо выяснить, хватит ли стульев для оказавшейся в комнате группы людей. Можно подсчитать отдельно количество стульев, отдельно — количество людей и сравнить два получившихся числа. Можно же попросить, чтобы каждый человек в одиночку сел на один стул. После того, как все люди усядутся, мы, не зная ни количества стульев в комнате, ни количества людей, тем не менее, точно сможем сказать, какое из этих количеств больше: в зависимости от того, останутся ли свободными стулья или — стоящими люди. В математике такой способ сравнения множеств называется установлением соответствия (отображения) между множествами. Второй способ сравнения количеств более фундаментален, чем первый: конструкция числа элементов строится на основе установления соответствий между множествами.

Будем задавать соответствие между элементами множеств стрелками. Если из каждого элемента множества A выходит единственная стрелка и к элементам множества B приходит не более чем одна стрелка (рис.1), то такое соответствие из A в B называется инъекцией. Когда существует инъекция из A в B (на каждом стуле сидит один человек, и никто не занял несколько стульев сразу), мы говорим, что количество элементов в множестве A меньше или равно количеству элементов в множестве B. Если существует инъекция как из A в B, так и из B в A, то количество элементов в этих множествах одинаково. Поскольку с помощью соответствий можно сравнивать не только конечные, но и бесконечные множества, вместо термина “одинаковое количество элементов” используют термин “равномощность” и вместо понятия “количество элементов” — термин “мощность”. Натуральные числа — мощности конечных множеств — становятся названиями соответствующих классов равномощных друг другу совокупностей.

Сила структур. Приведу примеры структурированных множеств.

1) Множества с разбиениями. Указываются признаки элементов множества, по которым их следует считать эквивалентными. Группы эквивалентных элементов образуют непересекающиеся классы, на которые разбивается исходное множество.

Сообщество живых организмов, принадлежащих одному местообитанию, например, все особи пруда, по целому набору признаков разделяются на популяции организмов, принадлежащих одному биологическому виду.

Множество натуральных чисел разбивается на классы чисел, дающих при делении, например, на 3, одинаковый остаток: N = k0 È  k1 È  k2, где k0 = {3, 6, 9, 12, ...}, k1 = {1, 4, 7, 10, ...} и k2 = {2, 5, 8, 11, ...}.

2) Множество с законами композиции. Для любых двух элементов a и b этого множества определен третий элемент c, называемый их композицией.

В множестве целых чисел для двух любых элементов определен третий — их сумма.

В алгебре логики с двузначным пространством истинности {истина (и), ложь (л)} определен ряд логических операций (законов композиции). Например,

Конъюнкция:

Ù

и

л

или дизъюнкция:

Ú

и

л
 

и

и

л

  

и

и

и
 

л

л

л

  

л

и

л

3) Метрические пространства. Для любых двух элементов a и b определено число S (a, b) такое, что S(a, a) = 0, S (a, b) = S (b, a) и S (a, c) £  S (a, b) + S (b, c).

Для точек и в трехмерном евклидовом пространстве определено S(, ) = .

Для структурированных множеств из всех возможных соответствий выделены те, которые сохраняют структуру множества. Эти соответствия называют морфизмами структуры.

Для экологического сообщества морфизмами, сохраняющими разбиение на виды, будут преобразования, состоящие в рождении или смерти особей. При этих преобразованиях биологический вид переходит в себя.

Для произвольных множеств с разбиениями по определению морфизмами служат соответствия, не перемешивающие классы эквивалентных элементов. Так, для отношения делимости чисел морфизмом будет числовая функция, заключающаяся в умножении на любое натуральное число y=n x (например, если x1 и x2 имели одинаковый остаток при делении на 3, то соответствующие y1 и y2 будут также иметь одинаковый остаток).

Для закона сложения целых чисел морфизмом будет, например, преобразование, состоящее в замене знака числа y Þ  -x: a + b = c Þ -a+(-b)=-c.

Одним из морфизмов метрической структуры является преобразование вращения в пространстве, — вращения сохраняют метрику пространства.

Количественное сравнение между собой неструктурированных множеств легко обобщить на множества, обладающие одинаковыми структурами. Структура множества A считается слабее структуры множества B, если существует инъективный морфизм структуры из A в B. Например, разбиение множества A на рис.2 оказывается слабее разбиения множества B.

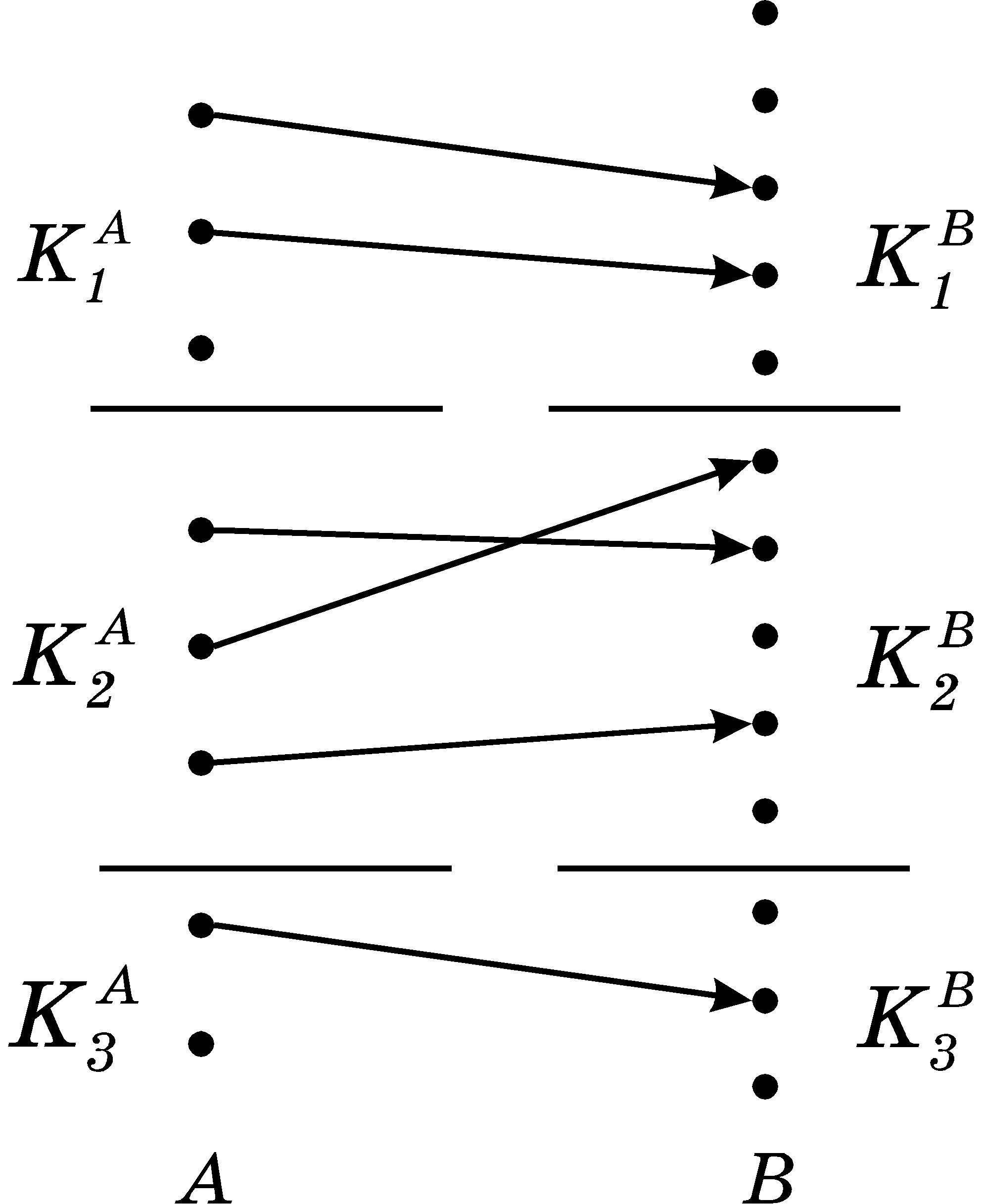
Так же, как сравнение с помощью инъекций неструктурированных множеств порождает понятие количества элементов в множестве (натуральные числа, мощности), так и сравнение структурированных множеств с помощью морфизмов порождает структурные числа структурированных множеств. По количеству элементов мы можем сравнивать любые множества, так как для любых двух множеств выполняется принцип трихотомии: количество элементов в A меньше, чем в B; или количество элементов в A больше, чем в B; или количество элементов в A равно количеству элементов в B. Т.е. всегда существует инъекция или из A в B, или из B в A, или и та и другая. Структурированные множества упорядочены структурными числами лишь частично, — существуют пары структурированных множеств, для которых ни прямой, ни обратной инъекций, сохраняющих структуру, не существует. На рис.3 приведен пример множеств с разбиениями, между которыми нет инъективных морфизмов.

Функторное сравнение структур. Частичная упорядоченность структурных чисел и возникающие порой, технические трудности при обнаружении инъективных морфизмов для некоторых структур заставляют продолжить поиск путей количественного сравнения структурированных множеств. Путь, на котором поиск мог бы оказаться удачным, хорошо разработан в математике. Речь идет о представлении одних математических структур другими математическими структурами.

Свойства вращения геометрического пространства можно эффективно изучать с помощью умножения определенных матриц.

Вся теория меры, в частности, измерение длин, площадей и объемов в геометрии есть пример количественной параметризации, основанной на представлении геометрических структур в числовые структуры анализа.

Равносильные математические описания нередки в физике: состояния атома в квантовой механике могут описываться векторами бесконечномерного гильбертова пространства (подход Шредингера) и бесконечными матрицами (подход Гейзенберга).

Поскольку при количественном сравнении одинаково структурированных множеств нам приходится иметь дело не только с самими структурированными множествами, но и в большой степени с морфизмами их структуры, дальнейшее изложение удобно вести на языке математической теории категорий, который специально предназначен для изучения совокупностей, куда на равных правах входят структурированные множества и их морфизмы.

Функтор — это отображение одной категории в другую, при котором объекты переходят в объекты, морфизмы — в морфизмы и обязательно сохраняется композиция морфизмов. Функторы оказываются представлением структур одной категории структурами другой.

Выделенные морфизмы категорий порождают упорядочение ее объектов. Так, в предыдущих абзацах мы сравнивали структурированные множества с помощью инъективных морфизмов. Если функторное представление монотонно относительно упорядочения в категориях (“структура объекта A сильнее структуры объекта B в категории S1” влечет “структура объекта F(A) сильнее структуры объекта F(B) в категории S2”, где F — функтор из S1 в S2), то предъявление монотонного функтора составляет функторный метод сравнения структур: об упорядочении объектов A и B в какой-либо категории со сложной и непривычной структурой можно судить по упорядочению их образов F(A) и F(B) в категории с простой или хорошо изученной структурой объектов (в цитированной выше книге (Левич, 1982) приведены достаточные условия монотонности функтора).

 

Инварианты структур. Стандартный функтор из произвольной категории структурированных множеств в категорию неструктурированных множеств, сопоставляющий объекту A множество всех морфизмов Hom(X, A) из фиксированного объекта X в объект A, оказывается монотонным при упорядочении структурированных множеств инъекциями. Таким образом, если структура объекта A сильнее структуры объекта B, то количество сохраняющих структуру преобразований произвольного объекта X в объект A больше, чем количество таких же преобразований из объекта X в объект B. Если структуры объектов A и B одинаковы, то количества преобразований в множествах Hom (X, A) и Hom(X, B) равны. Поэтому число преобразований в множестве Hom(X, A) удобно назвать инвариантом структуры объекта A относительно объекта X и обозначить (A).

Если структурированные объекты сравнимы, то их инварианты упорядочены так же, как объекты. Однако мы знаем, что структурированные множества могут оказаться несравнимыми. В этом случае может быть полезным принцип продолжения упорядочения структур по упорядочению их инвариантов: структура объекта A полагается сильнее (относительно объекта X) структуры объекта B, если IX(A) ³  IX(B).

Функторное сравнение структур можно рассматривать как дальнейшее обобщение понятия количества: от количества элементов бесструктурных множеств (задаваемого сравнением множеств с помощью инъекций) через структурные числа структурированных множеств (задаваемые сравнением множеств с помощью инъективных морфизмов структур) к числовым инвариантам структур. По-видимому, приведенные конструкции — не единственный путь обобщения представлений о количестве. Возможен путь поиска иных функторов в категорию множеств, или выбор иной параметризирующей категории вместо категории множеств, или выбор вместо инъекций других специальных морфизмов для сравнения объектов в исходной категории (и соответственно — иного функтора в параметризирующую категорию) и т.д.

Приведу пример сравнения структур с помощью инвариантов. Рассмотрим структуру множеств с разбиениями. Допустимыми служат морфизмы, переводящие каждый класс разбиения одного множества целиком в определенный единственный класс другого множества. Если — класс i разбиения множества X,  — класс разбиения множества A, в который переходит класс i, то общее количество морфизмов есть

.

Если морфизмы, например, отображения, и в классе Ki содержится ni элементов, то

.

Если допустимыми являются не отображения класса в класс, а какие-либо произвольные соответствия из класса в класс, то формула инварианта сохраняет вид произведения по классам с измененными сомножителями. В таблице приведены формулы для сомножителей при всех возможных комбинациях канонических свойств соответствий.

Замечу, что инварианты многих (а может быть, и произвольных) математических структур выражаются через ассоциированные с этими структурами разбиения, поэтому их инварианты имеют характерный вид произведения инвариантов отдельных классов разбиения.

Таблица

Количество соответствий из множества X (с количеством элементов x) в множество A (с количеством элементов a). Ck означает множество C с количеством элементов в нем k. Нижние индексы означают, что подсчитывается количество соответствий, обладающих теми свойствами, обозначения которых вошли в индексы:

p — всюду определенные соответствия;

f — функциональные соответствия;

i — инъективные соответствия;

s — сюръективные соответствия.

, где TA — множество всевозможных покрытий множества A

 

Энтропия систем. Вернемся к понятию инварианта структур и отметим два обстоятельства. Первое, если задана категория Q структурированных множеств, то инвариант объекта A из Q имеет смысл количества морфизмов в Hom(X,A). Другими словами, есть количество таких преобразований структурированного множества X в структурированное множество A, что они сохраняют задаваемую категорией Q для своих объектов структуру. Преобразования из X в A можно рассматривать, как допустимые структурой системы способы получить состояние A из состояния X, а в таком случае есть число таких способов. В статистической физике способы преобразования состояний, которые не меняют это состояние, обычно называют микросостояниями (подразумеваемый при этом образ: выделенный объем газа, состоящего из молекул, в котором допустимы переобозначения, перестановки и другие преобразования молекул, не меняющие давление, температуру и величину выделенного объема). Таким образом, понятие инварианта состояния системы можно интерпретировать как присущее этому состоянию число микросостояний.

И второе, число преобразований морфизмов зависит как от числа элементов в множествах X и A, так и от типа структуры, заданной на этих множествах. Чтобы исключить зависимость от числа элементов, сохранив зависимость от структуры, следует рассмотреть удельный инвариант , где — инвариант тех же по мощности множеств X и A, но в категории “бесструктурных” множеств, т.е. множеств со “стертой” структурой категории Q.

Учитывая два сделанных замечания, введем величину

.

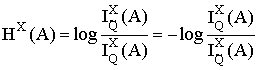Смысл ее — логарифм удельного числа преобразований состояния X в состояние A, или удельного числа способов получения состояния A из X (иногда такое число способов отождествляют с вероятностью образования состояния). Указанные интерпретации оправдывают употребление для величины HX(A) термина “энтропия состояния A относительно состояния X” по аналогии с больцмановским подходом к определению энтропии.

Как уже говорилось, инварианты многих (если не всех) математических структур выражаются через инварианты ассоциированных со структурами разбиений. Инварианты множеств с разбиениями мультипликативны относительно инвариантов каждого из классов разбиения, поэтому логарифмы инвариантов, входящие в энтропию, аддитивны и имеют характерный “энтропиеобразный” вид сумм по классам разбиения.

Формулы для энтропии получаются вне каких-либо статистических предпосылок. Например, если допустимые морфизмы есть отображения, то формула

,

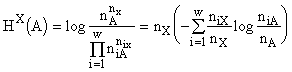где и , справедлива при любых, пусть самых малых, n. Введя pi=ni/n и представляя набор величин pi, i= как функцию распределения для состояния A, можно ввести вероятностную интерпретацию энтропии.

Рассмотрим еще два толкования вводимой формулы:

  1. Энтропия HX(A) может рассматриваться как мера “структурированности” состояния A (относительно состояния X), или — мера отклонения, “удаленности” структуры состояния A от его бесструктурного аналога.

  2. В формуле энтропии знаменатель есть инвариант структурированного множества A. Неравенство означает, что структура множества A слабее (по отношению к объекту X) структуры множества B в смысле отношения порядка “сила структур”. Пусть для состояний системы A и B числители
в формуле энтропии одинаковы, т.е. состояния A и B являются различными реализациями некоторой структуры на одинаковых по мощности базовых множествах, например, различными разбиениями одного и того же множества или группами, равномощными как множества. Тогда максимум энтропии и реальное состояние соответствуют минимальному (по “силе структур”) состоянию системы. Таким образом, энтропия играет ту же роль, что и инварианты математических структур, упорядочивая сами структуры и описываемые математическими структурами состояния естественных систем.

В силу приведенных выше доводов, экстремальность энтропии можно интерпретировать как экстремальность структуры описываемого ею состояния, а принцип максимума энтропии — как принцип реализации состояния системы с экстремальной структурой.

Определение энтропии именно через удельный инвариант структуры — дань традиции вводить нормированные на один элемент системы количества информации, разнообразия и т.п. Возможно, более последовательным в выбранном подходе было бы использование “неудельного” инварианта структуры, т.е. введение энтропии просто как логарифма количества допустимых структурой системы преобразований. Такая энтропия сохраняет свойства самого инварианта: она одинакова для состояний с одинаковыми по силе структурами и больше для тех состояний, структура которых сильнее, а также энтропия определена для всех состояний системы, т.е. она обобщает понятие “количество элементов бесструктурных множеств” на множества со структурой. И экстремальный принцип “максимума энтропии” приобретает смысл максимальной экспансии систем.

Отдельного обсуждения требует “относительность” введенного понятия энтропии, т.е. роль состояния X, относительно которого вычисляется энтропия HX(A) состояния A. Традиционный, не связанный с выделенным состоянием X, вид энтропии получится при расчете инвариантов состояния A относительно самого себя: H(A)=HA(A).

Статистические, вероятностные и связанные с информацией или разнообразием определения энтропии можно считать частными реализациями ее функторного определения. Связь же термодинамического определения энтропии со статистическими демонстрируется решением вариационной задачи на максимум статистической энтропии с ограничениями на получаемый поток теплоты. Абсолютная температура при этом оказывается величиной, обратной к соответствующему множителю Лагранжа.

Заключение

В зависимости от области приложения энтропийного подхода возникают самые разнообразные толкования энтропии — как меры неопределенности (Трайбус, 1970); меры “незнания” истинного микросостояния системы, находящейся в известном макросостоянии (Gell-Mann, 1994); меры порядка-беспорядка, сложности и организованности (Хайтун, 1996); меры неточности контроля над частицами (Губин, 1997); а также как разновидности функционала действия в гамильтоновой механике (Хазен, 1998).

Подобные интерпретации кажутся мне вторичными по отношению к той, которую вкладывал в термин “энтропия” Р.Ю.Клаузиус (Clausius, 1865), переводя с греческого τροπη κак “превращение”, или, имея в виду роль второго закона термодинамики для развития Мира, как “эволюцию”. Происхождение энтропии из рассмотрения допустимых системой преобразований сохраняют эту традицию.

В последующих статьях о роли энтропии я хотел бы раскрыть возможности приложения обозначенного подхода к энтропийной параметризации времени, к интерпретациям H-теоремы Больцмана, к обобщению теоремы Гиббса о дуализме между требованиями максимума энтропии и минимума энергии систем, к разрешению противоречия между деградационными и прогрессивистскими следствиями применения принципа максимума энтропии (Аршавский, 1982; Иванов, 1999). Также хотелось бы привести примеры приложения предложенного формализма к описанию реальных систем.

* Работа поддержана грантом Российского гуманитарного научного фонда №00-03-360а

Цитированные литературные источники:

Аршавский И.А. Физиологические механизмы и закономерности индивидуального развития. М.: Наука. 1982. 270 с.

Губин В.Б. История с энтропией//Философские науки. 1997. Вып. 3-4. Сс. 98-120.

Иванов А.Ф. Развитие и энтропия//Проблема развития в гуманитарном и социально-экономическом знании. С-Пб.: 1999. Сс. 16-18.

Климонтович Ю.Л. Физика открытых систем. М.: Янус. 1995. 624 с.

Коганов А.В. Векторные меры сложности, энтропии и информации//Математика. Компьютер.Образование. Вып. 7. М. 2000.

Колмогоров А.Н., Гельфанд И.М., Яглом А.М. К общему определению количества информации//Доклады Академии наук СССР. 1956. Т. 111. С.745.

Левич А.П. Теория множеств, язык теории категорий и их применение в теоретической биологии. М.: Изд-во Моск. ун-та. 1982. 190 с.

Мандельброт Б. Теория информации и психологическая теория частот слов//Математические методы в социальных науках. М.: Прогресс. 1973. Сс. 326-327.

Пригожин И.Р. От существующего к возникающему. М.: Наука. 1985. 328 с.

Приц А.К. Принцип стационарных состояний открытых систем и динамика популяций. Калининград. 1974. 123 с.

Хазен А.М. Введение меры информации в аксиоматическую базу механики. М.: Рауб. 1998.

Хайтун С.Д. Механика и необратимость. М.: Янус. 1996. 448 с.

Хинчин А.Я. Понятие энтропии в теории вероятности//Успехи математических наук. 1953. Т.8. №3. Сс. 3-20.

Boltzmann L. Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen // Sitzber. Acad. Wiss. Wien. 1872. Bd. 66. S. 275-376.

Clausius R. Über verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie//Ann. Phys. Folge 2. 1865. Bd. 125. S. 353-400.

Eddington A.S. The nature of the Physical World. Ann Arbor: University of Michigan Press. 1958.

Franklin W.S. Entropy and time//Phys. Rev. 1910. V. 30. P.776.

Gell-Mann M. The Quark and the Yaguar. London: Little, Brown. 1994.

Gibbs J.W. Elementary Principles in Statistical Mechanics, Developed with Especial Reference to the Rational Foundation of Thermodynamics. N.Y.: Schribner. 1902. 159 p.

Gzyl M. The method of Maximum Entopy. Singapore, New Jersey, London, Hong Kong: World Scientific. 1995.

Jaynes E.T. Informational theory and statistical mechanics//Phys. Rev. 1957. V. 106. Pp. 620-630.

Lotka A. Contribution to the energetics evolution//Proc. Nat. Acad. Sci. USA. 1922. V. 8. № 6. Pp. 147-151.

Lurie D., Wagensberg J. On biomass diversity in ecology//Bull. of Мath.Biol. 1982. V. 45. № 2. Pp. 287-293.

MacArthur R.H. Educations of animal populations and measure of community stability//Ecology. 1955. V. 36. № 7. Pp. 533-536.

Shannon C.E. A mathematical theory of communications//Bell Systems Tech. J. 1948. V. 27. Pp. 623-656.

Tribus M. Information theory as the basic for thermostatics and thermodynamics//J. Appl. Mech. Ser. E. 1961. V.28. № 1. Pp. 1-8.

Wilson A.G. Entropy in urban and regional modelling. London: Pion. 1970.