Успехи современной биологии, 2004, т. 124, № 6, с. 3-21.
© А.П.Левич
![]() Принцип максимума энтропии и теоремы вариационного моделирования
Принцип максимума энтропии и теоремы вариационного моделирования
А.П.Левич
Кафедра общей экологии Биологического факультета Московского государственного университета, Москва 119899, Россия. (095) 939-5560.
1. Введение
Обычный путь формального моделирования динамики систем – использование дифференциальных уравнений. Эти уравнения угадывают или получают феноменологически, формализуя эмпирические закономерности и пользуясь правдоподобными рассуждениями. Также существует подход, при котором постулируются не уравнения, а экстремальный принцип и вид экстремизируемого функционала. Сами уравнения становятся следствиями решения соответствующей вариационной задачи. Такой подход применяется как в задачах теоретической экологии (например, Lotka, 1922; Margalef, 1958; McArthur, 1969; 1970; Odum, 1971; Samuelson, 1974; Инсаров, 1975; Cohen, 1979; Schmelzer, 1981; Семевский, Семенов, 1982; Lurie et al., 1983; Mauersberger, Straškraba, 1987; Jorgensen, 1986, 1988, 1995; Страшкраба, Гнаук, 1989; Свирежев, 1991; Zeide, 1991; Jorgensen et al., 1995; Webb, 1995), так и при решении широкого круга общебиологических проблем. Одна из нерешенных задач состоит в углублении традиционного подхода, а именно, в попытке отыскать доводы не к угадыванию, а к выводу самих функционалов, на которых могло бы базироваться вариационное моделирование в экологии.
Известно, что угадыванию функционалов, например, в теоретической физике часто помогают соображения об их инвариантности к преобразованиям, допустимым физическими принципами. Предлагается аналогичные соображения отыскать для надорганизменных биологических систем.
Цель нынешней публикации — представить уважаемым читателям полученные к настоящему моменту теоретические и прикладные результаты вариационного моделирования в экологии сообществ. О степени осуществления замыслов предлагается судить по адекватности полученной вариационной модели и по предсказательной силе аналитических следствий модели в описании ими важных экологических принципов.
2. Экспериментальный контекст исследования
Исследованные экологические приложения модели относятся к группам организмов, нуждающихся в нескольких взаимонезаменимых ресурсах. Это могут быть, например, сообщества автотрофов, потребляющих углерод, азот, фосфор, кремний, энергию света и т.п. или сообщества бактерий, растущих на нескольких необходимых им одновременно субстратах. Речь идёт о существенно многовидовых сообществах конкурирующих за общие ресурсы организмов.
Модель описывает рост организмов на невозобновляемом запасе ресурсов. В лабораторных условиях этой ситуации соответствует накопительное, а не проточное культивирование. Замечу, что при проточном культивировании в отличие от накопительного не только возобновляется запас питательных веществ в среде, но и происходит изымание биомассы всех видов сообщества в одинаковой пропорции, обусловленной скоростью протока. Это обстоятельство существенно отличает проточное культивирование от процессов, протекающих в естественных условиях, где элиминация биомассы почти всегда видоспецифична. В то же время накопительное культивирование может служить прообразом некоторых естественных систем, например, водоёмов, в которых запасы биогенных элементов пополняются один-два раза в сезон при перемешивании обогащенных вод из-под термоклина с водными массами фотического слоя (Одум, 1986).
Изучается период развития от инокуляции до остановки роста, вызванной исчерпанием одного из ресурсов, но не какими-либо иными причинами (например, не аутотоксикацией, не аллелопатическими взаимодействиями и др.).
Учитывается, что рост организмов определяется не только запасами ресурсов в среде, но и внутриклеточными их запасами. А именно, подразумевается один из физиологических механизмов влияния запасов на рост: деление клеток прекращается, когда внутриклеточный запас по одному из взаимонезаменимых ресурсов достигает некоторого видоспецифического минимального значения (Droop, 1973). Учет указанного обстоятельства требует специальной экспериментальной проработки (Левич, Артюхова, 1991).
Верификация модели и апробация следующих из неё путей управления структурой сообществ проводились на данных о лабораторных и природных сообществах фитопланктона. Описание материалов и методик, на основании которых получены эти данные, приводятся в тех разделах работы, где упоминаются соответствующие эксперименты, чтобы избавить читателя от обращения к ранее прочитанному материалу.
3. Формулировка модели
Моделируется сообщество групп организмов, где группы различаются между собой по физиологическим потребностям в ресурсах (это могут быть популяции различных видов или другие физиологически однородные группы особей). Удобно описывать такое сообщество множеством из n элементов, разбитым на w непересекающихся классов с количеством элементов в классе ni (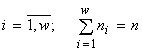 ), т.е. математической структурой множеств с разбиениями. Классы разбиения как раз соответствуют физиологически различающимся группам организмов. Набор численностей, входящих в сообщество видов
), т.е. математической структурой множеств с разбиениями. Классы разбиения как раз соответствуют физиологически различающимся группам организмов. Набор численностей, входящих в сообщество видов ![]() = {n1, n2,..., nw}, назову состоянием сообщества.
= {n1, n2,..., nw}, назову состоянием сообщества.
Постулируется, что динамические системы из заданного состояния переходят в состояние, обладающее экстремальной структурой и допустимое запасами ресурсов в системе. В настоящей работе предсказывается не динамика численностей в астрономическом времени, а конечное стационарное состояние сообщества — состояние, в котором остановился рост каждой из популяций в связи с исчерпанием запасов ресурсов как в среде, так и внутри клеток.
В силу этого обстоятельства используется следствие из приведенной выше локальной формулировки экстремального принципа: система оказывается в состоянии с наиболее экстремальной (в пределах, допускаемых имеющимися ресурсами) структурой.
Поскольку системы моделируются математическими структурами, то речь идёт о сравнении и выборе экстремальных объектов именно для математических структур. Категорно-функторный метод сравнения математических структур предлагает теорему, согласно которой произвольные математические структуры упорядочены так же, как их числовые инварианты (Левич, 1982; Levich, Solov’yov, 1999), а инварианты структур рассчитываются через количество допустимых рассматриваемой математической структурой морфизмов структуры (или на биологическом языке — допустимых преобразований сообщества). Замечу, что инварианты структур есть обобщение кардинальных чисел на структурированные множества и зависят как от мощностей базовых множеств, так и от свойств заданной на этих множествах структуры. Поэтому в модели должны фигурировать удельные инварианты, для которых элиминирована зависимость от базовых мощностей.
Рассматривается сообщество одноклеточных организмов, где допустимы смертность и деление клеток, но не допустимы их слияние и интродукция извне. В этом случае удельный инвариант структуры множеств с разбиениями есть (Levich, 1995):
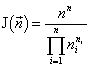 ,
,
где 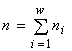 есть полная численность сообщества. Логарифм такого инварианта, названный обобщённой энтропией (Levich, 1995), есть
есть полная численность сообщества. Логарифм такого инварианта, названный обобщённой энтропией (Levich, 1995), есть
![]()
(более подробно связь инвариантов с больцмановским выражением для энтропии с индексами разнообразия и др. обсуждается в разделе 4.4).
Возникает вариационная задача на условный экстремум:
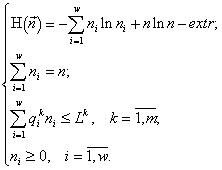 (1)
(1)
Здесь n и ni — искомые конечные численности, Lk — начальное содержание ресурса k в среде Lk ![]()
![]() ,
, ![]() — конечные клеточные квоты вида i по ресурсу k, m — общее количество взаимонезаменимых ресурсов, потребляемых сообществом, w — число видов в сообществе. Акцентирую внимание на том, что ограничения в задаче заданы в виде неравенств. Обоснование ресурсных ограничений состоит в необходимости выполнения законов сохранения для ресурсов, потребленных сообществом из среды.
— конечные клеточные квоты вида i по ресурсу k, m — общее количество взаимонезаменимых ресурсов, потребляемых сообществом, w — число видов в сообществе. Акцентирую внимание на том, что ограничения в задаче заданы в виде неравенств. Обоснование ресурсных ограничений состоит в необходимости выполнения законов сохранения для ресурсов, потребленных сообществом из среды.
4. Теоремы вариационного моделирования и их экологические следствия
4.1. Теорема стратификации
Формулировка теоремы (Левич и др., 1994). Все пространство ресурсных факторов 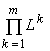 распадается (стратифицируется) на 2m-
1 непересекающихся областей (стратов), каждая из которых соответствует одному из подмножеств множества потребляемых сообществом ресурсов. В страте SJ, где J ¹
Æ
— подмножество множества ресурсов {1,2,...,m}, выполняется:
распадается (стратифицируется) на 2m-
1 непересекающихся областей (стратов), каждая из которых соответствует одному из подмножеств множества потребляемых сообществом ресурсов. В страте SJ, где J ¹
Æ
— подмножество множества ресурсов {1,2,...,m}, выполняется:
-решение задачи (1) ![]() , где
, где ![]() º
{L1, L2,..., Lm}, зависят
º
{L1, L2,..., Lm}, зависят
только от тех Lk, для которых kÎ J (отметим, что, как указано в разделе 4.2, решение (1) существует и единственно);
-на этом решении нестрогие неравенства 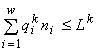 обращаются в строгие равенства для всех kÎ
J и в строгие неравенства для всех kÏ
J;
обращаются в строгие равенства для всех kÎ
J и в строгие неравенства для всех kÏ
J;
Теорема задает алгоритм расчёта стратов для заданного в сообществе набора квот ![]() . На рис.1 и 2 представлена стратификация пространства факторов среды для m = 2 и m = 3. Теорема стратификации влечёт редукцию задачи (1) к задачам:
. На рис.1 и 2 представлена стратификация пространства факторов среды для m = 2 и m = 3. Теорема стратификации влечёт редукцию задачи (1) к задачам:
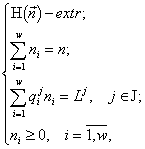 (2)
(2)
формулируемым для любого J Ì {1,2,...,m}.
Правило лимитирующего звена. Биологическая интерпретация теоремы стратификации задаёт правило лимитирующего звена для многовидовых сообществ, популяции из которых конкурируют за несколько ресурсов (Левич и др., 1993а). Назову лимитирующими ресурсы, потребляемые сообществом из среды полностью, т.е. те, для которых балансовые неравенства задачи (1) превращаются в равенства. Согласно теореме стратификации, из заданной совокупности ресурсов ![]() полностью потребляются, т.е. лимитируют рост сообщества, ресурсы из набора J, идентифицирующего страт SJ, которому принадлежит заданный вектор
полностью потребляются, т.е. лимитируют рост сообщества, ресурсы из набора J, идентифицирующего страт SJ, которому принадлежит заданный вектор ![]() . Таким образом, теорема стратификации позволяет строго предсказывать ресурсы, лимитирующие рост сообщества с заданным набором квот
. Таким образом, теорема стратификации позволяет строго предсказывать ресурсы, лимитирующие рост сообщества с заданным набором квот ![]() .
.
Для монокультур правило лимитирующего звена совпадает с принципом минимума Либиха (Liebig, 1840), а именно, при ![]() лимитирует фактор 1 (рис.3). Указанное условие эквивалентно
лимитирует фактор 1 (рис.3). Указанное условие эквивалентно ![]() , т.е. лимитирующим оказывается ресурс, для которого достигаемая на его запасе численность минимальна (т.е. тот, который в указанном смысле “находится в минимуме”). Замечу, что формально задача (1) не определена для w = 1, поскольку функционал в этом случае обращается в константу. Но решение задачи в этом случае может быть получено только из ресурсных ограничений, которые дают:
, т.е. лимитирующим оказывается ресурс, для которого достигаемая на его запасе численность минимальна (т.е. тот, который в указанном смысле “находится в минимуме”). Замечу, что формально задача (1) не определена для w = 1, поскольку функционал в этом случае обращается в константу. Но решение задачи в этом случае может быть получено только из ресурсных ограничений, которые дают:
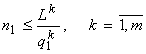 ,
,
т.е. реализуется 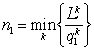 , или принцип минимума Либиха.
, или принцип минимума Либиха.
Для неодновидовых сообществ согласно правилу лимитирующего звена существуют как области, где рост ограничен одним фактором, так и несколькими, в частности, всеми факторами. Последняя ситуация в агрохимической литературе носит название “закона совокупного действия факторов” Митчерлиха (Mitscherlich, 1909). Эксперименты с фитопланктоном (Droop, 1973; Rhee, 1978; Ahlgren, 1980; Groot, 1983) демонстрируют предсказываемое переключение лимитирования.
Характер лимитирования при потенциальном ограничении роста сообщества, например, двумя ресурсами L1 и L2 рассчитывается следующим образом (Левич и др., 1993б). Пусть x0 — единственный корень уравнения 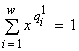 , а y0 — единственный корень уравнения
, а y0 — единственный корень уравнения 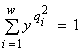 . Тогда величины
. Тогда величины 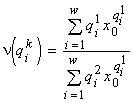 и
и 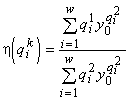 определяют границы области
определяют границы области ![]() , где рост сообщества ограничен обоими ресурсами L1 и L2. При
, где рост сообщества ограничен обоими ресурсами L1 и L2. При 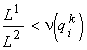 лимитирует первый фактор, а при
лимитирует первый фактор, а при ![]() — второй. В табл.1 приведен пример расчёта характера лимитирования при потенциальном ограничении роста альгоценоза азотом и фосфором. Примеры расчётов для других ценозов и для m >2 содержатся в цитированной выше работе (Левич и др., 1993а). Опишу прямой эксперимент по проверке правила лимитирующего звена. Для альгоценоза с известными потребностями видов
— второй. В табл.1 приведен пример расчёта характера лимитирования при потенциальном ограничении роста альгоценоза азотом и фосфором. Примеры расчётов для других ценозов и для m >2 содержатся в цитированной выше работе (Левич и др., 1993а). Опишу прямой эксперимент по проверке правила лимитирующего звена. Для альгоценоза с известными потребностями видов ![]() (
(![]() ) ставятся 2m-1 колб с принадлежащими каждому из стратов J начальными значениями
) ставятся 2m-1 колб с принадлежащими каждому из стратов J начальными значениями ![]() совокупности потребляемых ресурсов. После остановки роста содержимое каждой колбы разливается по 2m-1 новым колбам, в каждую из которых добавляют один из наборов ресурсов J. Возобновление роста во вторичной колбе с добавкой минимального (по включению) набора J указывает на лимитирование по этому набору ресурсов в соответствующей первичной колбе. Подобный эксперимент был проведён (Левич, Личман, 1992) с сообществом из трех видов микроорганизмов (зеленые водоросли Scenedesmus quadricauda (Turp.) Breb., Ankistrodesmus falcatus (Codra) Ralfs и цианобактерия Anabaena variabilis Kutz.), при различных начальных концентрациях азота и фосфора в среде. Квоты видов
совокупности потребляемых ресурсов. После остановки роста содержимое каждой колбы разливается по 2m-1 новым колбам, в каждую из которых добавляют один из наборов ресурсов J. Возобновление роста во вторичной колбе с добавкой минимального (по включению) набора J указывает на лимитирование по этому набору ресурсов в соответствующей первичной колбе. Подобный эксперимент был проведён (Левич, Личман, 1992) с сообществом из трех видов микроорганизмов (зеленые водоросли Scenedesmus quadricauda (Turp.) Breb., Ankistrodesmus falcatus (Codra) Ralfs и цианобактерия Anabaena variabilis Kutz.), при различных начальных концентрациях азота и фосфора в среде. Квоты видов ![]() и
и ![]() определялись в монокультурах тех же видов по специальной методике (Левич, Артюхова, 1991). Результаты эксперимента совпали с предсказанными наборами лимитирующих факторов (только азот, только фосфор или азот с фосфором совместно) для исходных значений концентраций веществ в среде.
определялись в монокультурах тех же видов по специальной методике (Левич, Артюхова, 1991). Результаты эксперимента совпали с предсказанными наборами лимитирующих факторов (только азот, только фосфор или азот с фосфором совместно) для исходных значений концентраций веществ в среде.
Подбор видов для сбалансированной утилизации многокомпонентных субстратов. Решение задачи по подбору видов содержит два этапа (Замолодчиков, Левич, 1992). Во-первых, следует выбрать матрицу квот ![]() так, чтобы границы страта полного потребления охватили бы заданный вектор ресурсов среды (например, конус с границами
так, чтобы границы страта полного потребления охватили бы заданный вектор ресурсов среды (например, конус с границами ![]() и
и ![]() для m = 2 и вектор
для m = 2 и вектор ![]() на рис.1). На втором этапе по найденной матрице
на рис.1). На втором этапе по найденной матрице ![]() можно подобрать реальные виды с нужными потребностями (квотами). Подобная задача может оказаться полезной в вопросах биологической очистки вод, составления сред для культивирования и т.п.
можно подобрать реальные виды с нужными потребностями (квотами). Подобная задача может оказаться полезной в вопросах биологической очистки вод, составления сред для культивирования и т.п.
4.2. Решение вариационной задачи
Формула видовой структуры. Достаточные и необходимые условия экстремума. Задачи (2) имеют решения
![]() , (3)
, (3)
где вектора ![]() ,
, ![]() и
и ![]() имеют компоненты j из набора J, идентифицирующего страт, которому принадлежит вектор
имеют компоненты j из набора J, идентифицирующего страт, которому принадлежит вектор ![]() . Множители Лагранжа
. Множители Лагранжа ![]() и полная численность n как функции потребляемых полностью в страте SJ ресурсов
и полная численность n как функции потребляемых полностью в страте SJ ресурсов ![]() ищутся из алгебраических уравнений
ищутся из алгебраических уравнений
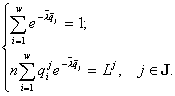 (4)
(4)
Показано (Левич и др., 1994), что решение (3) всегда существует, единственно и осуществляет максимум функционала ![]() . В прикладной экологии формула видовой структуры (3) позволяет рассчитывать:
. В прикладной экологии формула видовой структуры (3) позволяет рассчитывать:
-численности ni и n, если заданы запасы ресурсов Lk и потребности ![]() ;
;
-парциальные потребления лимитирующих ресурсов среды популяциями сообщества ![]() , если заданы суммарные потребления ресурсов
, если заданы суммарные потребления ресурсов ![]() (kÎ
J) всем сообществам
(kÎ
J) всем сообществам ![]() ;
;
-парциальные ![]() и полные
и полные ![]() реальные потребления нелимитирующих ресурсов, не входящих в страт SJ (kÏ
J).
реальные потребления нелимитирующих ресурсов, не входящих в страт SJ (kÏ
J).
-потребности видов ![]() , если известны численности популяций ni и потребления Lk (в m сериях опытов для m ресурсов).
, если известны численности популяций ni и потребления Lk (в m сериях опытов для m ресурсов).
Адекватность модели. Формула видовой структуры качественно объясняет происхождение ранговых распределений численности ni популяций в сообществах. Более подробно происхождение ранговых распределений обсуждается в разделе 5.1.
В опыте с поликультурой из 10-ти видов зелёных микроводорослей (Chlorella vulgaris (Bejerink.), Scotiella nivalis (Fritsch.), Chromochloris cinnoborina (Chodat.), S. quadricauda (Turp.), Scenedesmus bijugatus (Lagerh.), Scenedesmus obliquus (Kruger.), Ankistrodesmus acicularis (Korschik.), A. braunii (Brunnth.), Stichococcus mirabilis (Lagerh.) и Chlamydomonas humicola (Luksch.)) в течение 70 суток в нескольких повторностях измеряли численности и биомассы видов, первичную продукцию, концентрации минеральных форм азота и фосфора. В монокультурах тех же видов измеряли потребности клеток в фосфоре. Водоросли росли в накопительном режиме без барботажа на среде Бенеке. Содержание биогенных элементов в среде было подобрано так, чтобы развитие водорослей ограничивалось фосфором среды. На стационарной фазе роста распределение численности клеток описывалось формулой видовой структуры ![]() с коэффициентом множественной корреляции 0,97 (Левич и др. 1986). Эта же серия опытов наряду с ещё шестнадцатью сериями экспериментов была проанализирована с помощью ранговых критериев адекватности выборок и с помощью калибровки клеточных квот (Замолодчиков и др., 1993). Серии опытов отличались друг от друга наборами таксонов (от четырех до десяти видов в поликультуре) и начальными концентрациями азота и фосфора в среде (Левич и др., 1997). При лимитировании роста единственным ресурсом место вида в ранжированном по убыванию ряду численностей на стационарной фазе согласно формуле видовой структуры полностью определяется рангом клеточной квоты вида по лимитирующему ресурсу (наибольшая численность соответствует наименьшей клеточной квоте). Была сделана попытка подобрать в пределах экспериментальной ошибки единственный набор рангов измеренных в опыте клеточных квот так, чтобы воспроизвести экспериментальные ранги численностей уже во всех сериях, где рост был ограничен единственным ресурсом. Это удалось сделать с ранговым коэффициентом корреляции Спирмена в пределах от 0,92 до 1,00 (табл.2). Для серий с неоднофакторным лимитированием процедура проверки адекватности формулы видовой структуры состояла в следующем. По численностям видов в паре серий рассчитывали клеточные квоты по азоту и фосфору, а для всех остальных серий с этими откалиброванными квотами по формуле видовой структуры рассчитывали численности видов и сравнивали их с экспериментальными значениями. Сравнение показало, что рассчитанные значения численностей совпадают с измеренными в опыте в пределах экспериментальных ошибок.
с коэффициентом множественной корреляции 0,97 (Левич и др. 1986). Эта же серия опытов наряду с ещё шестнадцатью сериями экспериментов была проанализирована с помощью ранговых критериев адекватности выборок и с помощью калибровки клеточных квот (Замолодчиков и др., 1993). Серии опытов отличались друг от друга наборами таксонов (от четырех до десяти видов в поликультуре) и начальными концентрациями азота и фосфора в среде (Левич и др., 1997). При лимитировании роста единственным ресурсом место вида в ранжированном по убыванию ряду численностей на стационарной фазе согласно формуле видовой структуры полностью определяется рангом клеточной квоты вида по лимитирующему ресурсу (наибольшая численность соответствует наименьшей клеточной квоте). Была сделана попытка подобрать в пределах экспериментальной ошибки единственный набор рангов измеренных в опыте клеточных квот так, чтобы воспроизвести экспериментальные ранги численностей уже во всех сериях, где рост был ограничен единственным ресурсом. Это удалось сделать с ранговым коэффициентом корреляции Спирмена в пределах от 0,92 до 1,00 (табл.2). Для серий с неоднофакторным лимитированием процедура проверки адекватности формулы видовой структуры состояла в следующем. По численностям видов в паре серий рассчитывали клеточные квоты по азоту и фосфору, а для всех остальных серий с этими откалиброванными квотами по формуле видовой структуры рассчитывали численности видов и сравнивали их с экспериментальными значениями. Сравнение показало, что рассчитанные значения численностей совпадают с измеренными в опыте в пределах экспериментальных ошибок.
Инвариантность формулы видовой структуры. Система алгебраических уравнений (4) после исключения переменной n записывается в виде:
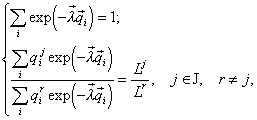 (5)
(5)
откуда следует, что множители Лагранжа lk и вместе с ними относительные численности ![]() зависят только от отношений ресурсов. Этот факт предоставляет возможность управления видовыми обилиями с помощью отношений ресурсов в среде (см. раздел 4.3).
зависят только от отношений ресурсов. Этот факт предоставляет возможность управления видовыми обилиями с помощью отношений ресурсов в среде (см. раздел 4.3).
Видовые обилия ![]() также инвариантны к преобразованием подобия квот
также инвариантны к преобразованием подобия квот ![]() (Левич и др., 1994), поэтому по формуле видовой структуры можно вычислить лишь отношения квот различных видов по каждому ресурсу, но не их абсолютные значения (этот факт также важен при калибровке модели).
(Левич и др., 1994), поэтому по формуле видовой структуры можно вычислить лишь отношения квот различных видов по каждому ресурсу, но не их абсолютные значения (этот факт также важен при калибровке модели).
Формула видовой структуры позволяет установить зависимость от ресурсов полной численности сообщества и его энтропийного индекса разнообразия (Левич и др., 1994):

где ½
J½
— количество лимитирующих ресурсов, соответствующее страту SJ; 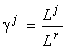 — отношения ресурсов, f и g — некоторые функции.
— отношения ресурсов, f и g — некоторые функции.
Примеры функции видовой структуры (обоснование расчётов содержится в работах Левич, 1980; Левич и др., 1994).
1) m = 1; qi = q1i; ni = 0,36![]() — экспоненциальное распределение численностей.
— экспоненциальное распределение численностей.
2) m = 1; qi = q1(1+lni); ni = 0,23![]() — гиперболическое распределение численностей. Рис.4 иллюстрирует экспоненциальное и гиперболическое ранговые распределения видовых обилий;
— гиперболическое распределение численностей. Рис.4 иллюстрирует экспоненциальное и гиперболическое ранговые распределения видовых обилий;
Результаты численных расчётов по формуле видовой структуры приведены на рис. 5, 6 и 7.
![]()
Результаты расчётов продемонстрированы на рис.11.
4.3. Теорема о максимуме видовых обилий
Аналитический результат. Как указывалось выше, из системы уравнений (5) следует, что относительные численности видов зависят только от отношений лимитирующих рост ресурсов среды. Доказано (Левич и др., 1993б; Alexeyev, Levich, 1997), что относительная численность некоторого вида принимает наибольшее возможное значение при отношениях ресурсов в среде, равных отношениям потребностей в этих ресурсах у данного вида. Рис. 12 иллюстрирует этот результат численным расчётом для случая m = 2, w = 4 и экспериментальных отношений квот.
Феноменологическая верификация теоремы. Существует ряд хорошо установленных феноменологических зависимостей, отражающих эмпирические представления о росте и потреблении фитопланктона. К ним относятся, в частности, закон Моно (Monod, 1942) для поглощения ресурсов из среды ![]() , закон Друпа (Droop, 1973) для зависимости скорости роста от внутриклеточных концентраций веществ
, закон Друпа (Droop, 1973) для зависимости скорости роста от внутриклеточных концентраций веществ ![]() , закон сохранения вещества и т.д. На основании этих зависимостей созданы имитационные модели, учитывающие эмпирические обобщения. Поскольку в такие модели заложены реалистичные описания данных, то модели должны как “большие аппроксимирующие формулы” имплицитно описывать “правильное” поведение сообществ. Исходя из этих предпосылок, гипотеза об управляющем влиянии отношений лимитирующих рост ресурсов была испытана на следующей имитационной модели (Йоргенсен, 1985):
, закон сохранения вещества и т.д. На основании этих зависимостей созданы имитационные модели, учитывающие эмпирические обобщения. Поскольку в такие модели заложены реалистичные описания данных, то модели должны как “большие аппроксимирующие формулы” имплицитно описывать “правильное” поведение сообществ. Исходя из этих предпосылок, гипотеза об управляющем влиянии отношений лимитирующих рост ресурсов была испытана на следующей имитационной модели (Йоргенсен, 1985):
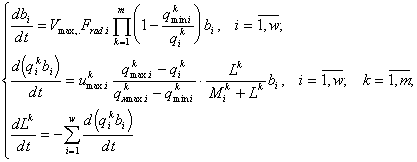
для w=3 и 4; m = 2 (Левич, Личман, 1992). Помимо уже введенных обозначений, здесь: bi — биомасса вида i; Vmax. и umax. — наибольшие скорости соответственно роста и поглощения, а ![]() соответствующая константа полунасыщения.
соответствующая константа полунасыщения.
После калибровки модели по данным экспериментов с лабораторным альгоценозом были проведены три машинных эксперимента соответственно с 45, 240 и 17 комбинациями начальных концентраций азота и фосфора. Зависимость видовых обилий от отношения N/P не закладывалась в модель. Результаты имитаций подтверждают гипотезу о зависимости относительных численностей от отношения N/P и о близости оптимального отношения N/P к отношению соответствующих откалиброванных минимальных квот для каждого из видов. (табл. 3, рис. 13).
Экспериментальная регуляция состава альгоценоза с помощью отношения ресурсов в среде. Собственные эксперименты проводились с лабораторными поликультурами и с сообществами естественного фитопланктона in vitro и in situ.
Многочисленные серии лабораторных экспериментов (Левич и др., 1997) отличались друг от друга составом альгоценозов и начальными концентрациями биогенных веществ в среде. В повторностях измерялись численности, объёмы клеток; концентрации ресурсов в среде как в поликультурах, так и в соответствующих монокультурах. Контролировались начальные внутриклеточные запасы лимитирующих ресурсов; нелимитирующие параметры: свет, температура, кислотность, микроэлементы; альгологическая и бактериологическая чистота, отсутствие метаболического взаимодействия. Рассчитывались потребления всем сообществом ресурса, клеточные потребности. Опыты в режиме накопительного культивирования продолжались до стационарной стадии роста. На рис. 14 приведены результаты двух экспериментов с двухвидовыми поликультурами (Левич, Булгаков, 1993). Замечу, что ни один из проведённых опытов не противоречил следствиям вариационного моделирования.
С естественным прудовым фитопланктоном in vitro проводились два опыта в различные сезоны (Левич и др., 1992). Прудовое сообщество содержало более сотни видов, принадлежащих к нескольким крупным таксонам: Chlorophyta (Chlorococcales, Chlamydomonadales, Desmidiales), Bacillariophyta, Cyanophyta. В одной из серий (20 литровые аквариумы) были испытаны три различных отношения азота к фосфору в интервале от 5 до 16, в другой серии (двухлитровые колбы) — пять отношений в интервале от 2 до 200. Опыты проводились в нескольких повторностях. Рис. 15 иллюстрирует основную тенденцию: для протококковых водорослей оптимальны высокие отношения N/P, а для синезелёных и диатомовых — низкие (на отношение N/P реагируют, конечно, не высшие таксоны, а доминирующие в них виды: в Chlorococales это S. quadricauda, в Cyanophyta — виды рода Microcystis, в Bacillariophyta — Nitzschia sp.). Замечу, что отношение qN/qP для S. quadricauda измеряется в десятках единиц (Левич, Артюхова, 1991), а для видов рода Microcystis оптимальное отношение составляет 5-10 (Rhee, Gotham, 1980). В описываемом опыте оценивалось влияние отношения N/P и на размерную структуру сообщества. Оказалось (рис.16), что с ростом величины N/P растёт биомасса классов мелких клеток и убывает — крупных (естественно, что меняются не размеры клеток, а доля в сообществе видов, имеющих соответствующие размеры).
Исследования in situ вели (Levich, Bulgakov, 1992; Левич и др. 1996 а,б) в течение 3-х лет на семи экспериментальных рыбоводных прудах от 0,25 до 3,5 га и глубиной около 1,5 м. В опытные и контрольные пруды с начала апреля вносили минеральные азот и фосфор в различных пропорциях: N/P = 4 в контрольных прудах и N/P = 25-50 – в опытных. Кроме того, привлекались данные о фитопланктоне и гидрохимических характеристиках тех же прудов в другие сезоны (всего около 20 “годопрудов”). Исследовали биомассы популяций фитопланктона, контролировали гидрохимические показатели прудов. Высокие отношения N/P приводили к увеличению доли протококковых водорослей и снижению доли синезелёных (в составе которых доминировали неазотфиксирующие виды). Рис. 17 иллюстрирует типичную динамику относительных биомасс для одного из прудов в одном из сезонов.
Многочисленные лабораторные опыты с проточным культивированием штаммов и природного фитопланктона обнаруживают существование оптимальных видоспецифичных отношений для концентраций азота, фосфора, кремния (Tilman, 1982; Sommer, 1983; Kilham, 1986; Suttle, Harrisson 1988; Grover, 1989; Suttle et al., 1991; De Pauw, Naessens-Foucquaert, 1991; Holm Armstrong, 1991; Egge, Haimdal, 1994; Grover 1997).
В природных водах первые наблюдения роли отношений веществ для развития фитопланктона относятся ещё к 30-м годам (Pearsall, 1930). Показательны работы Смита (Smith, 1983; 1986; 1995), который проанализировал данные по десяткам озёр мира и обнаружил, что доля синезелёных в озёрных альгоценозах резко падает при превышении для атомных отношений N/P значения, равного 25. Тилман (Tilman, 1982) назвал обнаруженную закономерность “драматическим воздействием отношения N/P на таксономический состав озёр.” Широко известна серия многолетних экспериментов на малых озёрах Швеции (Schindler, 1977; Findley, Kasian, 1987; 1994), где изменение отношения N/P также приводило к смене типа цветения водоёма. Зависимость высокого обилия синезелёных от низких отношений N/P (или высокого обилия зелёных при высоких значениях N/P) была замечена в озёрах США (McQueen, Lean, 1987; Stockner, Shortreed, 1988), Юго-восточной Азии (Cho et al., 1990), Южной Африки (Haarhoff et al., 1992), Франции (Michard et al., 1996). Обратнопропорциональная зависимость между численностью синезелёных водорослей и величиной N/P показана путём статистического корреляционного анализа для многих озёрных экосистем (Varis, 1991).
Одним из возможных механизмов подобных обнаруженных зависимостей численностей синезелёных и зелёных водорослей от отношения N/P может быть выявленная теоремой о максимуме видовых обилий зависимость оптимального отношения N/P от отношения соответствующих потребностей клеток (в тех случаях, если для доминирующих в ценозах видов зелёных водорослей это отношение высокое, а для синезелёных — низкое).
Модельные и эмпирические данные о роли отношений N/P для видовой и размерной структур фитопланктонных сообществ позволили сформулировать концепцию направленного регулирования типов цветения водоёмов с помощью биогенного манипулирования (Левич, 1995a; Levich, 1996). В вопросах деэвтрофирования регулирование с помощью отношения N/P предоставляет возможность парадоксального управления. А именно, обычный путь деэвтотрофирования состоит в сниженнии фосфорной нагрузки (стрелка АВ на рис. 1). Но если для доминирования цианобактерий действительно существенно низкое отношение N/P, а не абсолютные дозы биогенных веществ, то переход от цветения водоема синезелёными к цветению, например, протококковыми можно добиться и добавками азотных соединений в водоёмы (стрелка АС на рис. 1), что технически и экономически гораздо доступнее, чем изъятие фосфора или его ограничение в стоках. Возникающая при повышенных дозах питательных веществ дополнительная первичная продукция (теперь уже в виде биомассы протококковых) легко может быть утилизирована и превращена во вторичную продукцию консументами (например специально индуцируемыми в водоём фитопланктоядыми рыбами), поскольку зелёные водоросли в отличие от многих таксонов синезелёных не являются трофическим тупиком и, как правило, не токсичны. Переход из области однофакторного лимитирования (точка А на рис. 1) в область двухфакторного (точка С на рис. 1) к тому же гарантирует отсутствие накопление биогенных веществ в среде в виду их полного сбалансированного потребления.
Регуляция состава фитопланктонного сообщества может оказаться полезной и в случае оптимизации (по видовому или биохимическому составу, по размерной структуре) кормовых фитопланктонных сообществ при выращивании беспозвоночных, растительноядных рыб и других форм аквакультуры (Левич и др., 1996a; Левич и др., 1996б).
Увеличение доли синезелёных с помощью снижения отношения N/P в среде может оказаться полезным в целях обеззараживания сточных вод при их использовании для полива или в целях улучшения биологических свойств поливных вод.
4.4. Интерпретации и обсуждение экстремальных принципов. Теорема Гиббса
Экстремизируемый инвариант и энтропия. Экстремизируемый в рассмотренных вариационных задачах функционал ![]() , названный в разделе 3 обобщённой энтропией, был получен как логарифм удельного инварианта, возникшего при упорядочении описывающих систему математических структур. Сходство величины H с формулой для больцмановской энтропии не случайно, поскольку и инварианты структур и статистическая энтропия рассчитываются как количества некоторых преобразований (в случае статистики о них говорят как о “микросостояниях”). Однако, полученный в нашем случае при функторном сравнении структур функционал никак не связан со статистическим контекстом: его применение не требует ни больших численностей ni, ни большого числа видов w.
, названный в разделе 3 обобщённой энтропией, был получен как логарифм удельного инварианта, возникшего при упорядочении описывающих систему математических структур. Сходство величины H с формулой для больцмановской энтропии не случайно, поскольку и инварианты структур и статистическая энтропия рассчитываются как количества некоторых преобразований (в случае статистики о них говорят как о “микросостояниях”). Однако, полученный в нашем случае при функторном сравнении структур функционал никак не связан со статистическим контекстом: его применение не требует ни больших численностей ni, ни большого числа видов w.
Конкретный вид формулы обобщённой энтропии зависит от типа допустимых структурой исследуемой системы преобразований. В табл. 4 в качестве иллюстрации сведены некоторые из вариантов функторных инвариантов структур (Левич, 1982).
Подстановка решения задачи (1) — формулы видовой структуры (3) — в формулу для энтропии представляет энтропию как функцию лимитирующих развитие системы ресурсов
![]() .
.
В термодинамическом случае, когда речь идет о максимуме энтропии газа при ограничении только потоком тепла L1 º D Q, получаем H = DQ/T, где 1/Tєl1 -- соответствующий множитель Лагранжа. Тем самым устанавливается связь “обобщенной энтропии” H с энтропией феноменологической термодинамики.
Таким образом, применённый экстремальный принцип может рассматриваться как одна из модификаций или, если это покажется приемлемым, как обоснование принципа максимальной энтропии (Boltzmann, 1964; Gibbs, 1902; Jaynes, 1957; Фейнман, 1975; Levine, Tribus, 1978; Haken, 1988; Gzyl, 1995), нашедшего широчайшее применение в задачах из самых различных областей - от чистой математики и теоретической физики до экологии и лингвистики.
Энтропийному принципу эквивалентны и другие термодинамические экстремальные принципы:
Максимум энтропии H с ограничением по энергии Е влечёт минимум функции Лагранжа F=E-TH, называемой в термодинамике свободной энергией (связь абсолютной температуры T с множителем Лагранжа указана двумя абзацами выше).
Величина e = T(Heq.-H), где Heq. — энтропия системы в состоянии термодинамического равновесия, называется в термодинамике эксергией (т.е. энергией, которая может быть преобразована в полезную работу при участии заданной окружающей среды). С. Йоргенсен (JШrgensen, 1986; 1988; JШrgensen et al., 1995) в контексте экологического моделирования выдвинул и результативно применил принцип максимума эксергии: изменения воздействий на систему будут вызывать изменения структуры системы, которые сопровождаются неотрицательными изменениями эксергии. Величина эксергии с точностью до множителя совпадает с экстремизируемым в данном подходе логарифмом удельного инварианта систем (“обобщённой энтропией”). Таким образом, предложенный в данной работе экстремальный принцип представляет собой модификацию принципа максимальной эксергии С. Йоргенсена, дополненную нетермодинамическим методом расчёта энтропии.
Сложность, информация, самоорганизация, экспансия, мера структурированности, “устойчивость”, разнообразие. “Энтропийное” происхождение функционала H порождает для него ещё несколько возможных интерпретаций:
Мера сложности систем.
Количество информации, заключённой в структуре системы (JШrgensen, 1995; Левич, 1978).
Степень самоорганизации системы (Климонтович, 1995; Левич, 1995б).
В своей первоначальной формулировке (раздел 3) обсуждаемый экстремальный принцип постулируется как реализация состояний системы с экстремальной структурой. Конструкция сравнения структурированных множеств (Бурбаки, 1965; Левич, 1982; Levich, Solov’yov,1999) аналогична конструкции сравнения бесструктурных множеств по мощностям. Поэтому предложенный экстремальный принцип обобщает на многовидовые сообщества принцип максимальной экспансии (в пределах доступных ресурсов), подразумеваемый обычно в биологии для отдельных популяций.
О функционале ![]() можно говорить как о мере структурированности сообщества, т.е. как о степени удалённости разбиения множества от его бесструктурного аналога. И мы возвращаемся к формулировке экстремального принципа как принципа реализации экстремальной структуры.
можно говорить как о мере структурированности сообщества, т.е. как о степени удалённости разбиения множества от его бесструктурного аналога. И мы возвращаемся к формулировке экстремального принципа как принципа реализации экстремальной структуры.
Для систем с одинаковой мощностью базового множества n величина удельного инварианта 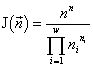 будет наибольшей, если минимален знаменатель
будет наибольшей, если минимален знаменатель 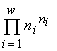 . Эта величина есть количество допустимых структурой системы (в данном случае структурой разбиения на непересекающиеся группы особей) преобразований. Таким образом, экстремальный принцип сводится к требованию реализации состояния с наименьшим количеством допустимых преобразований, или, в указанном смысле, — наиболее “устойчивой” структурой.
. Эта величина есть количество допустимых структурой системы (в данном случае структурой разбиения на непересекающиеся группы особей) преобразований. Таким образом, экстремальный принцип сводится к требованию реализации состояния с наименьшим количеством допустимых преобразований, или, в указанном смысле, — наиболее “устойчивой” структурой.
Величину ![]() экологи применяют как индекс разнообразия видовой структуры сообществ (McArthur, 1955). Замечу, что рассмотрение сообществ с иными, нежели в предложенной модели (раздел 3), допустимыми преобразованиями приводит к формулам инвариантов структуры, совпадающими с другими известными индексами разнообразия (подробнее см. раздел 5.1). В силу указанных отождествлений рассматриваемый экстремальный принцип может интерпретироваться как требование максимального видового разнообразия сообществ (см., например, Lurie et al., 1983).
экологи применяют как индекс разнообразия видовой структуры сообществ (McArthur, 1955). Замечу, что рассмотрение сообществ с иными, нежели в предложенной модели (раздел 3), допустимыми преобразованиями приводит к формулам инвариантов структуры, совпадающими с другими известными индексами разнообразия (подробнее см. раздел 5.1). В силу указанных отождествлений рассматриваемый экстремальный принцип может интерпретироваться как требование максимального видового разнообразия сообществ (см., например, Lurie et al., 1983).
Теорема Гиббса. Можно показать (Левич, Алексеев, 1997), что задача (1)

для любого ![]() равносильна задачам
равносильна задачам
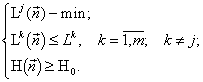
Таким образом, оказывается, что вместо формулировки экстремального принципа “энтропия системы максимальна, при условии, что потребление ресурсов ниже определённого запаса” справедлива формулировка “потребление системой ресурсов минимально, при условии, что энтропия системы (или её сложность, разнообразие, и т.д.,) выше некоторого порога”, т.е. принцип максимума энтропии эквивалентен принципу минимума потребления системой лимитирующих ресурсов. Указанная теорема является обобщением теоремы Гиббса (Gibbs, 1902) о равносильности требования максимальности энтропии газа (при заданной энергии) процедуре минимизации энергии (при заданной энтропии).
О принципе полного потребления. В контексте интерпретации энтропийного экстремального принципа полезно сопоставить его с другими возможными экстремальными принципами. Рассмотрим балансовые ограничения из (1), представляющие собой законы сохранения ресурсов, в качестве самостоятельных исходных предпосылок для моделирования:
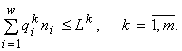 (6)
(6)
Можно показать (Левич, Лебедь, 1987), что в системе (6) в равенстве могут обратиться все неравенства, а могут только некоторые из них. Матрица потребностей (клеточных квот) ![]() порождает в пространстве ресурсов
порождает в пространстве ресурсов ![]() выпуклый конус (рис. 18) — линейную оболочку, натянутую на вектора
выпуклый конус (рис. 18) — линейную оболочку, натянутую на вектора ![]() , — внутри которого (и только внутри), исходя из законов сохранения (6), все m ресурсов могут потребиться полностью. Для вектора ресурсов
, — внутри которого (и только внутри), исходя из законов сохранения (6), все m ресурсов могут потребиться полностью. Для вектора ресурсов ![]() c вершиной вне этого конуса полностью потребляются ресурсы, для которых оси пространства ресурсов перпендикулярны тем граням параллелепипеда с диагональю
c вершиной вне этого конуса полностью потребляются ресурсы, для которых оси пространства ресурсов перпендикулярны тем граням параллелепипеда с диагональю ![]() , которые пересекаются с конусом полного потребления.
, которые пересекаются с конусом полного потребления.
Для модели (6) можно ввести экстремальный принцип “полного потребления”: ресурсы, которые могут быть потреблены полностью согласно законам сохранения, обязательно потребляются полностью.
Если ориентироваться на принцип полного потребления, то вместо задачи с неравенствами (1) следует сформулировать задачу
 (7)
(7)
где в множество индексов T входят ресурсы, полностью потребляемые согласно законам сохранения (6).
Конус полного потребления задачи (6) оказывается более широким, чем криволинейный конус полного потребления из теоремы стратификации для задачи (1) (см. раздел 4.1). Это обстоятельство позволяет попытаться сделать выбор между энтропийным экстремальным принципом и принципом полного потребления с помощью обращения к эксперименту: на рис. 19 приведены различающиеся в пространстве между конусами зависимости численностей от величины L1/L2 в двухфакторной задаче.
5. Экологический смысл модельных конструктов
5.1. Происхождение ранговых распределений
Если пронумеровать группы организмов в порядке убывания их численностей, то номер группы i называют рангом группы, а зависимость численностей групп n(i) от их ранга — ранговыми распределениями. Ранговые распределения численностей (или биомасс) представляют собой действенный инструмент количественного исследования структуры экологических сообществ и нормирования нарушающих структуру воздействий.
В качестве групп могут выступать биологические таксоны; размерные классы; совокупности особей, объединенные по каким-либо физиологическим или иным признакам. В обзорах по применению ранговых распределений в экологии (Левич, 1980; Frontier, 1985; Пузаченко, 1996) можно найти немало ссылок на исследования сообществ планктона, бентоса, перифитона, птиц, млекопитающих, насекомых, высших растений и многих других организмов.
Для феноменологического описания ранговых распределений (Левич, 1980) в экологии применяются различные аппроксимации: экспоненциальная модель n(i) ~ zi, гиперболическая модель ![]()
![]() , объединяющее их дзета-распределение
, объединяющее их дзета-распределение ![]() ~
~![]() , модель “разломанного стержня”
, модель “разломанного стержня” ![]() ~
~![]() (в формулах n(i) обозначает численность особей ранга i; z, b и B — параметры моделей).
(в формулах n(i) обозначает численность особей ранга i; z, b и B — параметры моделей).
Формула видовой структуры (3) (см. раздел 4.2) объясняет происхождение ранговых распределений.
Пусть m = 1, т.е. потребляется единственный ресурс. Пусть потребности видов в этом ресурсе распределены линейно: qi º
q1i. Тогда формула видовой структуры задает экспоненциальное ранговое распределение ni /n = zi, где ![]() z =
z =![]() (см. также примеры в разделе 4.2). Пусть потребности видов распределены по закону qi =q1 ln(B + i), тогда ni /n ~ 1/(B + i)b, где b =
(см. также примеры в разделе 4.2). Пусть потребности видов распределены по закону qi =q1 ln(B + i), тогда ni /n ~ 1/(B + i)b, где b = ![]() q1. Для такого медленно меняющегося распределения потребностей, как qi ~ lnlni, получаем распределение численностей, близкое к задаваемому моделью “разломанного стержня” распределению ni ~ -lni. В случае двух ресурсов и распределений потребностей
q1. Для такого медленно меняющегося распределения потребностей, как qi ~ lnlni, получаем распределение численностей, близкое к задаваемому моделью “разломанного стержня” распределению ni ~ -lni. В случае двух ресурсов и распределений потребностей ![]() и
и ![]() получаем двухпараметрическое дзета-распределение численностей. Становится понятной резко убывающая форма ранговых распределений: согласно формуле видовой структуры, численности экспоненциально зависят от монотонных распределений потребностей. Таким образом, распределение численностей полностью порождается распределением их потребностей. См. также другие примеры в разделе 4.2. Рис.4. иллюстрирует эмпирические ранговые распределения для фитопланктона.
получаем двухпараметрическое дзета-распределение численностей. Становится понятной резко убывающая форма ранговых распределений: согласно формуле видовой структуры, численности экспоненциально зависят от монотонных распределений потребностей. Таким образом, распределение численностей полностью порождается распределением их потребностей. См. также другие примеры в разделе 4.2. Рис.4. иллюстрирует эмпирические ранговые распределения для фитопланктона.
5.2. Биологическое разнообразие
Происхождение индексов разнообразия. Параметры ранговых распределений (множители Лагранжа модели) отражают скорость (резкость, выровненность, равномерность, однородность и т.п.) убывания численностей от группы к группе или, что то же, степень доминирования групп с высокой численностью. Эти параметры называют индексами видового (в случае распределения видов) разнообразия и обычно вычисляют по приближенным формулам: для экспоненциальных ранговых распределений — ![]() (Margalef, 1951), для гиперболических распределений —
(Margalef, 1951), для гиперболических распределений — ![]() при b=2 (Menhinik, 1964) или
при b=2 (Menhinik, 1964) или ![]() при b=1 (Odum et al., 1960). Эти индексы выделяют в класс параметрических (Левич, 1980).
при b=1 (Odum et al., 1960). Эти индексы выделяют в класс параметрических (Левич, 1980).
Другой класс образуют императивные индексы разнообразия типа энтропийного индекса 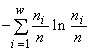 (McArthur, 1955), индекса Симпсона
(McArthur, 1955), индекса Симпсона 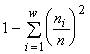 (Simpson, 1949) или индекса Пилоу
(Simpson, 1949) или индекса Пилоу 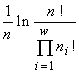 (Pielou, 1975). Эти индексы однозначно связаны с инвариантами математических структур, порождающими функционалы вариационной модели. Энтропийный функционал возник (см. раздел 3) при моделировании сообщества структурой множеств с разбиениями, а также со смертностью и делением клеток в качестве допустимых преобразований (инъективные и сюръективные, но не функциональные и не всюду определённые соответствия в табл.4). Если допустить, кроме названных преобразований, поглощение одних организмов другими и интродукцию особей извне (произвольные соответствия в табл.4), то удельный инвариант приобретает вид
(Pielou, 1975). Эти индексы однозначно связаны с инвариантами математических структур, порождающими функционалы вариационной модели. Энтропийный функционал возник (см. раздел 3) при моделировании сообщества структурой множеств с разбиениями, а также со смертностью и делением клеток в качестве допустимых преобразований (инъективные и сюръективные, но не функциональные и не всюду определённые соответствия в табл.4). Если допустить, кроме названных преобразований, поглощение одних организмов другими и интродукцию особей извне (произвольные соответствия в табл.4), то удельный инвариант приобретает вид 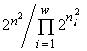 , а экстремизируемый функционал — логарифм инварианта —
, а экстремизируемый функционал — логарифм инварианта — 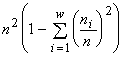 , т.е. оказывается пропорциональным индексу разнообразия Симпсона. Если допустимо только неизменное существование особей (инъективные, функциональные, всюду определённые и сюръективные соответствия), то удельный инвариант структуры множеств с разбиениями есть
, т.е. оказывается пропорциональным индексу разнообразия Симпсона. Если допустимо только неизменное существование особей (инъективные, функциональные, всюду определённые и сюръективные соответствия), то удельный инвариант структуры множеств с разбиениями есть 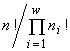 , а экстремизируемый функционал оказывается пропорциональным индексу разнообразия Пилоу.
, а экстремизируемый функционал оказывается пропорциональным индексу разнообразия Пилоу.
Таким образом, вариационная модель позволяет сознательно выбирать индекс разнообразия, адекватный структуре и состоянию сообщества. А именно, императивные индексы разнообразия определяются математической структурой, принятой для описания сообщества, и допустимыми его функционированием преобразованиями. Параметрические же индексы порождаются экстремизацией некоторого императивного индекса и, кроме того, зависят от матрицы потребностей (квот) видов и запаса ресурсов в среде.
Теорема о биологическом разнообразии. Согласно вариационной модели можно утверждать, что биологическое разнообразие есть следствие ограниченности биогенных ресурсов на Земле. Точнее, справедлива теорема: неограниченность ресурсов влечёт возможность существования только одновидовых сообществ. Действительно, решение методом неопределённых множителей Лагранжа вариационной задачи (1) без ресурсных ограничений влечет требование равенства нулю частных производных по ni и n от функции Лагранжа ![]() , что, в свою очередь, позволяет выразить ni и n через множители l: ni = n = el-1, а подстановка их в условие связи
, что, в свою очередь, позволяет выразить ni и n через множители l: ni = n = el-1, а подстановка их в условие связи 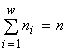 влечёт w = 1.
влечёт w = 1.
5.3. Экологический смысл множителей Лагранжа
Интерпретация множителей Лагранжа (во всяком случае при m = 1) как параметрических индексов разнообразия уже была продемонстрирована в разделе 5.2.
Другая интерпретация связана с анализом размерности множителей Лагранжа. В виду безразмерности показателя экспоненты в формуле видовой структуры (3), размерность множителя lk обратна размерности потребностей ![]() . Т.е. величина 1/lk может быть пропорциональна имеющей ту же размерность средней по сообществу потребности в ресурсе k. (Замечу, что в случае термодинамики идеального газа при заданной энергии выполняется 1/l = T, где абсолютная температура T пропорциональна средней кинетической энергии молекул.)
. Т.е. величина 1/lk может быть пропорциональна имеющей ту же размерность средней по сообществу потребности в ресурсе k. (Замечу, что в случае термодинамики идеального газа при заданной энергии выполняется 1/l = T, где абсолютная температура T пропорциональна средней кинетической энергии молекул.)
Ещё одна интерпретация связана с теоремой вариационного моделирования, утверждающей, что
![]()
(Lankaster, 1968), т.е. множитель Лагранжа lk является скоростью изменения энтропии H при изменениях ресурса k, поэтому его можно интерпретировать (Интрилигатор, 1975) как “силу влияния” фактора k на “целевую функцию” H.
6. Заключение
Работы в области вариационного моделирования могут быть продолжены в нескольких направлениях.
Дальнейшего развития требует категорно-функторный базис модели. В частности, необходимо формальное, а не эвристическое обоснование формулы удельного инварианта. Возможны расчёты функционалов для сообществ с более сложными типами структур, например, с возрастной или трофической структурами.
Желательна “локальная”, а не глобальная формулировка экстремального принципа, позволяющая описывать траектории системы, а не только стационарные состояния. Поиск динамических уравнений может оказаться перспективным на пути выбора динамических систем, для которых вычисляемая обобщённая энтропия является функцией Ляпунова.
Доступно решение вариационных задач для иных, нежели рассмотренный в настоящей работе, функционалов и ограничений; доступны формулировки и доказательства соответствующих аналогов уже имеющихся теорем, формализация подходов к учёту потребления взаимозаменимых ресурсов, моделирование эксплуатируемых популяций и т.п.
Необходима дальнейшая опытная верификация следствий модели, в частности проведение описанных выше экспериментов по проверке правила лимитирующего звена и по выбору между энтропийным экстремальным принципом и принципом полного потребления. Интересен поиск физиологических механизмов, ответственных за реализацию теоремы о максимуме видовых обилий в случае равенства для организма отношений внешних и внутренних концентраций лимитирующих ресурсов.
Заслуживает внимания приложение идей вариационного моделирования в экологии к описанию техноценозов или экономических систем, функционирующих в условиях конкуренции за ресурсы (Левич, 1996).
Важное прикладное значение может иметь применение следствий вариационного моделирования к проблемам экологического нормирования. Дело в том, что конструкты модели (функционалы, множители Лагранжа, решения вариационной задачи) задают количественные закономерности, отклонение от которых может интерпретироваться как степень нарушенности нормального функционирования системы. Многие из этих конструктов, в частности ранговые распределения, параметрические и императивные индексы разнообразия, систематически используются в качестве интегральных оценочных характеристик в экологии сообществ (Левич, 1980; Левич, 1996). Вариационная модель позволяет осознанно выбрать адекватные исследуемой ситуации характеристики и осуществлять по биологическим показателям оценку экологического состояния природных объектов на шкале “норма-патология”. Наличие же такой оценки, в свою очередь, позволяет рассчитывать региональные нормативы экологически допустимых уровней для факторов среды, нарушающих экологическое благополучие (Левич, 1994; Левич, Терехин, 1997).
Cписок литературы