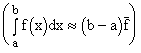 позволяет представить изменение предэлементов в объекте следующим образом:
позволяет представить изменение предэлементов в объекте следующим образом:ВРЕМЯ КАК ИЗМЕНЧИВОСТЬ ЕСТЕСТВЕННЫХ СИСТЕМ: СПОСОБЫ КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ИЗМЕНЕНИЙ
И ПОРОЖДЕНИЕ ИЗМЕНЕНИЙ СУБСТАНЦИОНАЛЬНЫМИ ПОТОКАМИ
Задача предлагаемого читателю исследования — обсудить один из возможных вариантов конструкции времени, точнее, подготовить пролегомены к построению динамической теории естественных систем, последовательно предложив элементарный объект теории, способы изменчивости объектов, часы, пространство состояний, способы вывода законов изменчивости и, по возможности, — интерпретирующие процедуры. Также в задачу работы входит испытать конструкцию на решении некоторых проблем времени.
Предлагаемые материалы не составляют законченного исследования. Их следует воспринимать лишь как попытку создания исследовательской программы по изучению времени.
1.1. Субституционная конструкция времени
Системы и изменчивость. Естественные системы складываются из элементов не произвольным образом.
Принцип иерархичности. Естественные системы иерархичны: любой объект оказывается элементом объекта более высокого ранга и любой элемент оказывается объектом, состоящим из предэлементов.
Так, живая клетка состоит из молекул, организмы складываются из клеток и сами объединяются в популяции, популяции составляют сообщества, которые, в свою очередь, могут рассматриваться как элементы биосферы. Это фрагмент биологической иерархии.
Вариант геологической иерархии — молекулы, минералы, породы, отложения, рельефы...…
Географическая иерархия — это молекулы, отложения, фации, урочища, ландшафты, физико-географические районы, провинции, зоны, страны, материки, суша, географическая оболочка (по И.А.Солнцеву из книги И.И.Михайлова, 1985).
Эскиз астрономической иерархии — молекулы, тела, планетные системы, звездные ассоциации, галактики... (все приведенные примеры имеют смысл лишь иллюстраций, конкретизирующих общие рассуждения, но не строгих построений).
Иерархическое строение систем — не только естественнонаучное обобщение, но и один из способов аксиоматизации теории множеств, позволяющий избежать логических противоречий, связанных с бесконтрольным построением объектов из элементов: если каждому элементу приписать тип, то множества (естественные объекты) образуются из элементов одинакового типа (Whitehead, Russel, 1910; Френкель, Бар-Хиллел, 1966). Типы объектов обычно маркируются натуральными числами. Существенно, что в предлагаемой аксиоматике все понятия приобретают типовый характер: при строгом изложении (Левич, 1982) предъявление любой конструкции — объект, элемент, принадлежность, объединение или пересечение, время, пространство и т.д. — должно сопровождаться указанием типа, и лишь при неформализованном изложении, когда тип конструкции хорошо ясен из контекста, его указание нередко опускается.
При рассмотрении иерархических систем обычно возникают вопросы о том, насколько далеко “вверх” и “вниз” простираются уровни иерархии. Автору удобно занять позицию, в силу которой глубина иерархии определяется наличием операциональных способов различения элементов “удаленных” уровней. Для любой имеющейся в момент исследования технологии различения существует уровень неразличимых элементов, который и будет приниматься за границу иерархии (относительную — с учетом возможности изменения доступных методов исследования объектов).
Количество учитываемых уровней строения удобно называть глубиной системы. Принцип иерархичности требует, чтобы элементарный объект теории — “система” — обязательно представлял собой иерархическую конструкцию (рис.1).
Будем понимать под изменением набора элементов системы появление в ней новых элементов (рост системы) или замены уже имеющихся элементов на иные их экземпляры (стационарное состояние системы), или потери элементов (деградация и разрушение системы).
Принцип изменчивости. Во всех естественных системах существует обязательный феномен изменения набора составляющих систему элементов. Любое изменение системы состоит в изменении набора элементов на уровне определенной глубины в иерархии, содержащей систему.

Явление изменения набора элементов в системе я буду называть генеральным процессом для естественных систем.
Приведу описания генеральных процессов для объектов канонического примера биологической иерархии.
В живых клетках генеральным процессом является метаболизм, в процессе которого заменяются молекулы в составе клетки. Генеральный процесс для многоклеточных организмов — рост, при котором появляются новые клетки и заменяются или исчезают уже существующие. Динамика численности, резюмирующая рождения и смерти особей, составляет генеральный процесс для популяции. Смена видов, называемая сукцессией, есть проявление генерального процесса в экологических сообществах. Смена ассоциаций живых организмов в биосфере Земли называется процессом эволюции.
Принципы иерархичности и изменчивости позволяют унифицировать разнообразие проявлений изменчивости (изменение качеств, отношений, связей и т.д.) — изменяются только количества или экземпляры элементов системы. Качественная специфика изменений описывается принадлежностью замен элементов различным уровням строения системы, т.е. описать изменчивость — значит отыскать иерархические уровни системы, на которых происходят изменения в наборах предэлементов.
Следует заметить, что термин “изменчивость” часто используется не только в динамическом смысле. Говорят о пространственной (например, географической) изменчивости биологических или социальных объектов. В терминах изменчивости описывают и разнообразие объектов в таксонах каких-либо их классификаций (атомы в системе химических элементов, бабочки в коллекции). Встав на позицию историзма, можно попытаться свести все типы изменчивости к появлению их в результате только динамической эволюционной изменчивости, но в рамках настоящей работы предлагается ограничиться обсуждением проявлений “чистой” динамической изменчивости естественных объектов.
Наряду с терминами “изменение набора элементов” и “генеральный процесс” предлагается синоним “течение времени”. Таким образом, постулат существования предвремени заменен постулатом существования генерального процесса. Не проясняя “природы” времени, такая модификация, тем не менее, оказывается полезной, операционально задавая события как замены элементов системы.
Измерение времени. Генеральный процесс, унифицируя изменчивость, вводит предвремя естественных систем. Чтобы ввести параметрическое время, т.е. представление процесса изменчивости числами, понадобится методологическое отступление.
“В процессе измерения, столь простом по существу, замечается значительная недоговоренность во многих курсах механики и физики, ставших классическими; установить большую определенность в этом вопросе и вместе с тем показать, сколь большой произвол имеет место при установлении измерения, и было моей задачей” (Фридман, 1965, с.16).
А именно, если на множестве K свойств некоторого фрагмента реальности задано отношение порядка, то эти свойства называются интенсивностями. Если для интенсивностей K1, K2 и K3 определено отношение “равноотстояния”: K1 настолько меньше K2, насколько K2 меньше K3, то эти интенсивности называются измеримыми. Например, объемы геометрических тел — измеримые интенсивности, а степень знания учащихся — не измеримые.
Отображение A:K ® R класса свойств K в числовое множество R называется арифметизацией свойств K. Монотонная арифметизация интенсивностей называется оценкой. Примеры: оценка степени знания учащихся по пяти- или стобалльной шкале; сопоставление цветам спектра солнечного света длин соответствующих электромагнитных волн. Оценки измеримых интенсивностей, удовлетворяющие свойству A (K2) -A (K1) = A (K3) - A (K2), называются измерениями. Любые две арифметизации, являющиеся измерениями, могут лишь линейно отличаться друг от друга началом отсчета или единицей измерения.
Итак, “всякий класс свойств может быть арифметизирован; если свойства эти делаются (путем нашего определения) интенсивностями, то мы можем... оценить их числами; наконец, если интенсивности делаются (опять-таки путем нашего определения) измеримыми интенсивностями, то мы можем... их измерить; измерение будет включать в себе известный произвол, который устраняется, если мы установим начальное значение и единицу измерения” (Фридман, 1965, с.16).
Таким образом, для возможности измерения изменчивости требуется договоренность (инструкция, императив...) о различиях в интенсивностях изменчивости, принимаемых за равные.
Принцип императивности. Часами называется эталонный объект, принадлежащий определенному уровню строения системы. Изменения набора элементов эталонного объекта на один элемент считаются равными и могут быть приняты за единицу измерения времени.
Необходимость подобного соглашения осознана естествоиспытателями: “A priori мы можем взять любое динамическое явление и использовать его развивающийся процесс, чтобы определить масштаб времени. Однако не существует равномерного, естественного масштаба, так как мы не можем сказать, что имеем в виду под словом “равномерный” в отношении времени; мы не можем схватить текущую минуту и поставить рядом с ней последующую. Иногда говорят, что равномерный масштаб времени определяется периодическими явлениями. Однако разрешите задать вопрос: может ли кто-либо нам сказать, что два следующие друг за другом периода равны?” (Milne, 1948, с.5).
В физике роль соглашения о равномерности играет первый закон Ньютона: равными принимаются промежутки времени, за которые тело, не участвующее во взаимодействии с другими телами, проходит равные расстояния (Tompson, Tait, 1890).
Введем ряд определений для иллюстрации тех путей конструирования понятийного аппарата, что открываются после принятия принципа императивности.
Событие x типа i (синоним — момент времени) для объекта A типа i + 1 есть акт замены элемента x в объекте A. Также станем называть событием сам элемент x, заменяющийся в объекте A.
Субституционные часы — природный объект, замена элементов которого принята за эталон равномерной изменчивости.
Собственное время (Васильев и др., 1974), собственный возраст (Зотин, Алексеева, 1984) организма могут отсчитываться по потреблению организмом молекул кислорода.
Собственный возраст организма может быть измерен количеством вновь образованных клеток: площадью заживления ран (Noьy, 1936); ростом выделенных органов тела, например, размер хрусталика глаза у млекопитающих считается одним из лучших коррелятов биологического возраста (Shaher, 1982); количеством отпочковавшихся клеток у дрожжей, которые есть их единственная стабильная возрастная характеристика в отличие от любых хронологических датировок (Войтенко, 1985).
Шкала возрастных стадий растения (например, для овсеца (Чебураева, 1977): проростки, всходы, ювенильная, имматурная, молодая вегетативная, молодая, зрелая, старая, субсенильная, сенильная) рассматривается как особая форма учета онтогенетического времени, при этом интервалы между соседними возрастными стадиями принимаются за равные (Уранов, 1975). Так же — и в шкале, основанной на моментах появления междоузлий гороха (Thornwaite, 1953).
Динамику микроводорослевых популяций удобно описывать в шкале поглощенных клетками биогенных элементов, лимитирующих развитие сообщества (Левич, 1980; Левич и др., 1986). Параметр зрелости экологического сообщества (понятие, близкое к экологическому возрасту) вводят М.Е.Виноградов и Э.А.Шушкина (1983): индекс зрелости связан с отношением деструкции сообщества (часто измеряемой по убыли из системы биогенных химических элементов) к первичной продукции (пропорциональной вхождению биогенных веществ в сообщество).
В палеонтологии широко распространен анализ развития крупных групп организмов на основе измерения количества таксонов. Обычно используются характеристики, относящиеся к одному стратиграфическому подразделению: общее количество таксонов, количество появившихся и вымерших таксонов (Дмитриев, 1978).
Интервалом собственного времени глубины k между событием a типа k и событием b типа k для произвольной системы типа i называют количество элементов типа k, заменившихся в системе в результате генерального процесса, т.е. собственное время глубины k для системы типа i измеряется часами типа i -k+1, полученными как объединение элементов типа i -k+1, принадлежащих исходной системе.
Если удастся корректно ввести представление об одновременности событий, то возникнет возможность измерения не только собственного времени системы, но и ее времени по произвольным часам.
Внешнее время (время по часам С). Интервал времени по часам C между событиями a и b есть интервал собственного времени объекта C между событием x, принадлежащим C и одновременным с событием a, и событием y, принадлежащим C и одновременным с b.
Возраст T объекта A по каким-либо часам есть время по этим часам между событиями в объекте A, состоящими во входе элемента d в A и выходе d из A (d принадлежит A).
Количество кислорода, потребленное животными от “первого вздоха” до “последнего дыхания”, может служить физиологическим возрастом организма. Если справедливо правило Рубнера (Зотин, Алексеева, 1984), то это количество одинаково для всех представителей одного биологического вида. А в предположении постоянства коэффициента трат кислорода на окисление единицы массы пищи физиологический возраст организма соответствует количеству потребленной пищи, т.е. речь идет о некоторой субстратно-энергетической шкале собственного времени организма. Правило Рубнера подтверждается экспериментальными результатами, полученными в основном на грызунах, насекомых, одноклеточных: ограничение питания приводит к пролонгированию жизни (McCay, 1935; Бауэр, 1935).
Настоящее время объекта. Пусть заданы объект A типа i +k и его элемент d типа i. Назову “настоящим уровня k для объекта d относительно надобъекта A” интервал времени (по каким-либо часам) между событиями, состоящими во входе элемента d в A и в выходе d из A. Величину T указанного интервала можно назвать “толщиной настоящего”. Замечу, что толщина настоящего для объекта d относительно надобъекта A равна возрасту объекта A, измеренному по элементу d.
События, происходившие до входа объекта d в объект A, логично назвать “прошлым относительно надобъекта A”. Соответственно определяются и “будущие события объекта d относительно надобъекта A”. Очевидно, что настоящее, прошлое и будущее заданного объекта относительны, т.е. полностью зависят от выбора надобъекта A (а именно — вышележащего уровня естественной иерархии и представителя A на этом уровне, содержащего объект d).
Для введения настоящего, прошлого и будущего оказалась существенной многокомпонентность субституционного времени. Многокомпонентность позволяет операционально различать несовпадающие свойства времени: временна¢ я серия “прошлое — настоящее — будущее” для объекта d задается относительно его надобъектов, а серия “раньше — позже” задается часами, имеющими тот же тип, что и подобъекты объекта d.
Отмечу, что идеи, связанные с “толщиной настоящего” для неодномерного времени, индуцированы разработками Г.Е.Михайловского, представленными в настоящей книге.
Субституционное время и субституционный объект теории. “Substitucio” — по латыни “замена”. Конструкция часов, оперирующая заменами элементов в системах, по традиции привлечения латинских терминов в научные тексты названа субституционной. В дальнейшем в качестве синонима термину “субституционный” будет использоваться и термин “метаболический”, имеющий древнегреческое происхождение (Левич, 1986; 1989а; 1989б).
Научная традиция, идущая от Гераклита и Аристотеля, связывает время с восприятием и переживанием изменений в Мире. Аристотель (1981, комментарий 9 к главе 11 книги 4) различал изменения как движение в широком смысле (metabolě), как возникновение и уничтожение (genesis kai phthora), как качественные превращения (alloisis), как механические перемещения (kinesis)... . Предложенная аксиоматика изменчивости: “генеральный процесс — обобщенное движение — течение времени” — относится не к отдельным видам превращений и соответствует, по-видимому, термину metabolě. По предложению С.В.Мейена, описываемую конструкцию времени будем называть метаболическим временем естественных систем (см. также употребление термина в работах Г.Е.Михайловского (1982), Шмидт-Ниельсона (1987), Гудвина (1966)). Однако термин “метаболическое” предлагается понимать в гораздо более широком смысле, чем биохимический метаболизм живых клеток и организмов.
Обычно время воспринимается как тактовый, или связанный с повторяющимися периодами процесс: смена дня и ночи, колебания маятника и тиканье часов, ритм метронома... Измерение времени в физике всегда связано с периодическими процессами: вращением Земли, механическими или электромагнитными колебаниями. Предложенная конструкция заменяет “тактовые” часы на “субституционные”, перенося акценты на процессы, необязательно периодические, нестационарные, эволюционные. Впрочем, “тактовое” и “субституционное” представления процессов могут оказаться дополняющими друг друга.
В квантовой механике при описании физических полей существует глубокое соответствие между описаниями явлений на языке частот и на языке замен (“рождений” и “уничтожений”) частиц. Оно задается методом вторичного квантования.
Метаболическое время — свойство системы, обязательно не замкнутой по элементам какого-либо уровня ее строения.
Субституционная конструкция порождает архетип иерархического и метаболического видения Мира, точнее, естественных систем: элементарный объект теории непохож на “точки” или “состояния” — это объект иерархический и обязательно незамкнутый.
Для строгого описания метаболического объекта нужны и новые математические средства. Иерархичность объекта может быть описана конструкцией армад (Левич, 1982), которая явно вводит в математику, помимо переплетения традиционных алгебраической, топологической и порядковой структур (Бурбаки, 1963), также иерархическую математическую структуру (основанную на упоминавшейся выше теории типов). Однако теоретико-множественные основания математики, по-видимому, недостаточны для формализации метаболического объекта: нужен аппарат для описания универсумов с вновь появляющимися и исчезающими элементами (на это обстоятельство обратил внимание А.А.Шаров). Может быть, для этого достаточно принять более мягкую форму аксиомы экстенсиональности, но возможно, что для оперирования с “динамическими множествами” вместо совокупностей с раз и навсегда заданным объемом элементов потребуются и более радикальные средства. Хорошим имплицитным примером “динамического множества” может служить “метапопуляция” организмов, включающая в себя не только существующие ныне особи, но и всех их предков и потенциальных потомков.
Еще одна черта формального описания субституционного объекта — необходимость отказа от аксиомы Архимеда: никакое “механическое сложение” элементов предуровня не должно давать целостного объекта уровня, т.е. алгебраические свойства универсумов различных уровней таковы, что универсумы соотносятся между собой как объекты нестандартного анализа (Robinson, 1966).
1.2. Свойства субституционного времени
Многокомпонентность. Собственные времена системы различной глубины образуют многокомпонентную величину, которую в настоящем тексте предлагается называть “пирамидой времени” системы (см. рис.1). Термин “пирамида” выглядит достаточно неуклюжим, но напрашивающееся обозначение “вектор времени” было бы математически неточным, поскольку не введены ни система координат, ни преобразования, относительно которых изучаемая многокомпонентная величина вела бы себя как вектор.
Собственное время t1 глубины 1 для клетки измеряется количеством замененных в клетке молекул. Аналогично время организма исчисляется заменяющимися клетками (Noьy, 1936; Shaher, 1982). Популяционное время t1 определяется балансом рождений и гибелей членов популяции (Абакумов, 1969; Алексеев, 1975; Вернадский, 1980; Свирежев, Пасеков, 1982). Для сообщества t1 есть количество сменившихся в сукцессии видов. Биосферное время t1 отсчитывается сменяющими друг друга, исчезающими и вновь образующимися ассоциациями живых организмов.
Экологическое сообщество можно представить как объединение индивидуальных организмов всех образующих сообщество видов: баланс изменений общей численности будет задавать величину t2 собственного времени глубины 2 для сообщества. Для организма t2 определится потоком молекул через организм (Васильев и др., 1974). Биосферное время t2 есть число сменившихся в ходе эволюции видов (Дмитриев, 1978).
Для решения ряда количественных проблем экологии удобно представить сообщество как пул лимитирующего развитие организмов биогенного химического элемента (например, углерода, азота или фосфора). Сумма изменений количества молекул в пуле (на практике такие количества оцениваются в единицах массы или концентрации) составляет для сообщества собственное время глубины 3 (например, для альгоценозов, Левич и др., 1986а) или глубины 4 (для сообществ неодноклеточных организмов; Виноградов, Шушкина, 1983).
Обычно для измерения времени выбирают одну из компонент, почти всегда наиболее глубокую, находящуюся вблизи уровня неразличимости и связанную с физическими процессами (например, электромагнитную шкалу, соответствующую “заменам” фотонов в атомах). Принцип императивности позволяет выбирать в качестве эталонных часов систему любого уровня естественной иерархии.
Представления о неодномерности времени неоднократно возникали в естествознании. “Для жизни время — с геохимической точки зрения — выражается в трех различных процессах: во-первых, время индивидуального бытия, во-вторых, время смены поколений без изменения формы жизни и, в-третьих, время эволюционное — смены форм одновременно со сменой поколений” (Вернадский, 1988, с.231). “Множество временных шкал, несомненно, представляет собой важнейший аспект жизни... Например, существует физическое время (в уравнениях движения), каталитическое время (необходимое для описания ферментативных реакций), время клеточного деления, время экологических сукцессий и, наконец, эволюционное время...” (из письма Г.Патти К.Х.Уоддингтону. На пути..., 1970, с.177-178). Г.Е.Михайловский (1982) вводит комплексное время живых организмов (см. также главу Г.Е.Михайловского в настоящей книге). Действительная его часть представляет онтогенетическое время организма, а мнимая — определяется стадией процессов самовоспроизведения. На необходимости введения трехмерного биологического времени настаивает Н.И.Моисеева (1980).
Неравномерность хода. Свобода выбора эталонных объектов для измерения времени позволяет поставить вопрос: все ли процессы соизмеримы друг с другом, т.е. любой ли из существующих процессов может служить эталоном для любого другого процесса? На этот вопрос приходится отвечать отрицательно, поскольку в силу принципа императивности промежутки времени, одинаковые при измерении одними часами, могут оказаться неравными в показаниях других часов (схематический пример на рис.2 иллюстрирует взаимную неравномерность двух шкал).

Неравномерность метаболического времени — следствие принципов иерархичности и императивности — обнаруживается только при наличии нескольких временны'х шкал. Если шкала единственна, то ход времени равномерен по определению, составляющему содержание принципа императивности. Например: “Абсолютное, истинное, математическое время само по себе и по самой своей природе, без всякого отношения к чему-либо внешнему протекает равномерно и иначе называется длительностью. Все движения могут ускоряться или замедляться, течение ж абсолютного времени измениться не может” (Newton, 1687).
Выбор достаточно “глубинной” компоненты пирамиды времени в качестве единственного представителя всей пирамиды приводит к принятию эталона равномерности физических шкал. Создаваемые человеком приборы для измерения времени (например, сгорающая свеча с нанесенными на ней делениями, песочные, водяные, маятниковые, астрономические, атомные и пульсарные часы) обладают почти одинаковой взаимной равномерностью.
Заметим, что физические процессы, претендующие на эталонное использование (вращающаяся Земля, эфемеридное время, “второе всемирное” время, учитывающее сезонные поправки к вращению Земли, тропический год, излучение атомов цезия), предоставляют наблюдателям существенно (для современных требований точности) различающиеся по равномерности хода часы (Мартынов, 1961).
Выбор часов — во многом психологическая проблема: хотя в качестве эталонных могут быть предложены самые различные естественные процессы, но предпочитаются — удобные для человека. То есть те, что согласуются с ходом “времени сознания”, который в свою очередь индуцируется планетными условиями обитания человека. “В самом деле понятие равномерности движения уже предполагает наличность времени, а выражение “движение звезд совершается равномерно” означает только то, что мы называем движение звезд равномерным. Равномерность движения есть понятие совершенно относительное, — можно говорить о равномерности одного движения по отношению к другому, и когда мы говорим о равномерном движении, то подразумеваем под этим движение равномерное относительно движения звезд или, что звучит еще более одиозно, равномерное относительно вращения Земли. В признании за звездным временем особого мистического значения кроется нежелание человека понять всю нецентральность и скромность планеты, на которой, волею судеб, ему пришлось жить” (Фридман, 1965, с.53). Антропоморфическая выделенность шкал времени объяснима, но не должна заслонять возможностей применения в системах отсчета при описании различных форм обобщенного движения шкал с иными равномерностями хода времени.
Замена эталонных объектов и вместе с ней замена шкал, связанная с изменением равномерности хода времени, — это не замена единиц измерения или начала отсчета, а обязательно нелинейное преобразование, поскольку линейные трансформации сохраняли бы равномерность шкалы: равные промежутки времени оставались бы равными. Большинство “собственных” шкал времени в естествознании неравномерны относительно астрономического времени, что позволяет порою обнаружить закономерности, ускользающие при использовании традиционных физических шкал.
Шкала, основанная на скорости заживления ран (Noьy, 1936), оказывается неравномерной по отношению к хронологическому возрасту: рана пятилетнего ребенка заживает в десять раз быстрее, чем рана пятидесятилетнего человека.
Нелинейное преобразование планетного времени (Backman, 1943) при описании кривых роста широкого класса живых организмов позволило обнаружить элементарные длительности — “кванты жизни”, плотность которых равномерна в “органическом времени” Бакмана и на начальных этапах развития значительно более высока в обычной временно¢ й шкале (в силу чего кванты трудноуловимы).
Э.Милн (Milne, 1948) устранил постулат конгруэнтности временны'х интервалов, показываемых часами одного типа, а именно, механическими и атомными, и ввел логарифмическую шкалу для космологического времени Вселенной. Преобразование времени элиминировало гравитационное взаимодействие из фундаментальных уравнений движения и кардинально упростило описание нестационарности Вселенной.
Гипотеза логарифмической связи между временны'ми шкалами. Поскольку шкалы времени, задаваемые эталонами различных уровней, неравномерны относительно друг друга, возникает вопрос, какова функциональная связь между различными шкалами? Ряд исследователей предлагает логарифмическую зависимость некоторых специфических времен от обычного физического времени — это и упоминавшийся переход к космологическому времени Э.Милна (Milne, 1948), и “органическое время” Г.Бакмана (Backman, 1943), которое представляет собой параметризацию изменчивости живых организмов количественными характеристиками их роста. Размер хрусталика глаза пластинчатозубой крысы Nesocia indica (как индикатор биологического возраста) и ее хронологический возраст связаны логарифмической зависимостью (Shaher, 1982). Попытка подобрать статистическими методами наиболее адекватную аппроксимацию зависимости у крыс биологического возраста, определявшегося по 23 физиологическим характеристикам, от хронологического возраста — также привела к логарифмической функции (Hofecker, 1981).
Происхождение обнаруживаемой в опыте для некоторых шкал “закономерности логарифма” составляет одну из проблем описания неравномерности шкал многокомпонентного метаболического времени. Одна из попыток решения этой проблемы содержится в работе Б.С.Флейшмана (1986).
Специфичность временны'х шкал. Времена, задаваемые эталонами из различных уровней строения систем, и тем более из различных естественных иерархий не универсальны, а специфичны.
Если мы говорим о специфических временах, например, о физиологическом, онтогенетическом или эволюционном времени, это означает, что первое измеряется количеством поглощенных при дыхании молекул кислорода; второе — числом вновь образованных клеток растущего организма, а третье — числом таксонов в реконструируемой летописи биосферы.
Геологическое, биологическое, географическое и другие специфические времена есть пирамиды собственного времени, выстроенные в соответствующих естественных иерархиях.
Представление об универсальности времени возникает, поскольку обычно в пирамиде времени выделяется достаточно глубинная компонента, соответствующая физическим шкалам времени. Различные естественные системы часто обладают единством материального строения, например, биологическая, геологическая, географическая, астрономическая и другие иерархии включают уровень молекул и соответственно все предшествующие — физические — уровни. Это обстоятельство влечет возможность выбора единой шкалы для систем различной природы. Таким образом, привычная универсальность (или абсолютность, по терминологии И.Ньютона) времени связана с исключительным использованием шкал, задаваемых глубинными уровнями строения систем. Чем более глубок уровень иерархии, делегировавший эталонную систему, тем для более широкого набора систем вышележащих уровней пригоден эталон.
За универсальность времени, обусловленную применением “глубинных” эталонов, приходится расплачиваться определенной ценой – потерей представлений о структуре системы. Универсальность как бы “стирает” структуры уровней, лежащих выше уровня эталонной системы, из-за чего оказываются несущественными характеристики генеральных процессов, происходящих в вышележащих уровнях.
Так, исследуя экосистему как объединение молекул, из которых состоят все биотические ее компоненты и оборачивающиеся в экосистеме неживые пулы веществ, можно многое сказать о вещественной основе функционирования подобных систем. В то же время на молекулярном языке трудно сформулировать представления о трофических связях видов, о возрастной, половой и других структурах популяции, о сезонной и иных сукцессиях, о поведении особей и ряде других немолекулярных процессов.
В физике роль “стирающего структуры” понятия часто играет энергия.
Применение специфических шкал позволяет эксплицировать свойства времени, задаваемые конкретными структурами систем, но приводит к “неразличимости” темпоральных свойств объектов на нижележащих уровнях строения системы. При этом выбор уровня эталонной системы и вместе с ней степени универсальности или специфичности задаваемой эталоном временно¢ й шкалы зависит от поставленных в исследовании целей.
Использование специфических шкал, нелинейных относительно привычного времени, может привнести в исследование простоту и адекватность описания явлений, надежду на выявление закономерностей, ускользающих при ином способе описания.
Так, например, при использовании метаболической шкалы, связанной с количеством молекул субстратов, поглощаемых клеточными популяциями при развитии культур микроводорослей, удалось обнаружить стадии роста и потребления, не проявляющиеся при анализе обычных кривых роста (Левич и др., 1986).
Измерение продолжительности стадий развития животных в детлафах (Детлаф, 1982; см. также гл.2 в настоящей книге) позволяет сравнивать времена развития как у животных различных видов, так и у одних и тех же видов, но в разных условиях развития (например, при неодинаковой температуре).
Проблема существования границ индивидуальной продолжительности жизни с трудом поддается анализу при измерении возраста в хронологических единицах. Анализ же в шкалах собственного времени, например, в единицах количества молекул потребленного организмом вещества, позволяет надеяться обнаружить естественные границы, которые связаны с видоспецифическим предельным тотальным количеством кислорода, поглощаемым организмом в течение жизни (в случае справедливости правила Рубнера (Зотин, Алексеева, 1984)).
Дискретность и аддитивность. Поскольку время определяется заменами элементов в системах, то вместе с дискретностью самих элементов дискретным оказывается и ход времени. Но степень дискретности временно¢ й шкалы (как и степень дискретности структуры системы) зависит от выбора глубины эталонного уровня для определения времени.
Назовем степенью дискретности эталонной шкалы величину 1/N, где N — количество элементов эталонного объекта, заменяющихся между появлением и исчезновением одного элемента в исследуемой системе.
Замена одного организма (N =1) в популяции соответствует заменам N =10-1013 его клеток или N ~ 1023 содержащихся в организме молекул, т.е. выбор глубинных шкал измерения времени приводит к резкому снижению степени его дискретности.
В шкале собственного времени из аддитивности субстрата следует и аддитивность метаболического времени. Если, однако, на каком-либо уровне строения дискретность и аддитивность субстрата отсутствуют (таковы, например, феномены психики или объекты в ландшафтоведении и биогеоценологии), то появляется и неаддитивность в свойствах времени. В этом случае представления о заменах элементов теряют определенность и для описания генерального процесса требуется специальный формальный аппарат (например, булевозначная теория множеств (Левич, 1982), в частности нечеткие множества).
Существование вневременны'хсобытий. Если в качестве эталона времени выбран объект уровня i, то измерение времени на уровне i -1 требует введения долей интервалов эталонной системы. Но применение долей для нижележащих уровней может оказаться неадекватным, так как их “равномерность” может не описывать процессы глубинных уровней. Имея конструкцию метаболических часов, нетрудно определить не только интервалы времени между событиями, но и длительности событий. При этом событие типа i оказывается вневременны¢ м (“мгновенным”) явлением в шкалах типа i и выше (но не в шкалах типа меньшего, чем i). Например, при выборе в качестве эталона электромагнитной шкалы оказываются вне динамического (и, возможно, вне причинно-следственного) анализа все предшествующие уровни строения систем.
Уже в квантовой механике существуют вневременны'е события: поглощение и испускание электромагнитных квантов атомами, т.е. переходы атома в иное энергетическое состояние; редукция волнового пакета; изменение квантовых чисел в одной из частей квантовой системы в результате процесса измерения над другой сколь угодно далеко удаленной ее частью (парадокс Эйнштейна—Подольского—Розена).
Поляризация. Замены элементов, образующие течение времени, неравноценны по отношению к содержащему элементы объекту: элементы могут входить в систему (возникать в ней) или выходить из системы (разрушаться, погибать). Поэтому интервал метаболического времени складывается из двух качественно различных слагаемых:
Dt=Dt+ + t-.
Пространство состояний и описание движения. Совокупность всех элементов одного типа (одного уровня естественной иерархии) удобно называть (Левич, 1982) универсумом этого типа (см. рис.1). Тогда пространство состояний системы, представляющей собой объект типа k, описывается декартовым произведением универсумов всех типов, меньших k (замечу, что в данной конструкции состояние системы — не точка, а подмножество пространства состояний; тогда, как обычно, состояние есть точка фазового пространства состояний). По отношению к пространству состояний о феномене генерального процесса удобно говорить как об “обобщенном”, “субституционном” или “метаболическом” движении системы.
Удачным наглядным образом такого движения является устройство “бегущей рекламы” или движение изображения на экране электронно-лучевой трубки.
Уровни иерархического строения системы могут теперь играть двоякую роль — роль пространственных измерений мира (“измерения” как компоненты пространства состояний) и роль временны¢ х измерений.
Например, о замене молекул в клетке можно говорить на языке течения времени (мысленный образ: неподвижная клетка с входящими в нее и выходящими вовне молекулами, отсчитывающими такты течения времени, — “клеткоцентристская” точка зрения). Можно о том же явлении говорить как о движении клетки в молекулярном пространстве, где движением назван переход от включения клеткой одной из молекул среды к включению другой (мысленный образ: неподвижные точки-молекулы и передвигающаяся от молекулы к молекуле клетка — “молекулоцентристская” точка зрения).
Принцип конвенциональности. Выбор “пространственных” или “временны'х” измерений мира среди уровней строения системы определяется договоренностью между исследователями.
Представление о метаболическом движении: любое движение объекта есть “поглощение” и (или) “испускание” им своих элементов (“точек” пространства, или среды, входящих в универсумы каких-либо предуровней иерархического строения объекта) составляет, на мой взгляд, одно из существеннейших методологических следствий метаболической конструкции.
Проводя попытку унифицировать представления о движении, следует обосновать границы правомочности экстраполяций. Предлагаемую конструкцию времени можно рассматривать в рамках двух вариантов ограничений на область ее применения.
Слабая гипотеза: конструкция относится лишь к надмолекулярным уровням строения материи, и такие термины, как “время”, “движение”, “пространство”, имеют лишь метафорический смысл.
Сильная гипотеза: механическое движение и физическое время обусловлены заменами элементов на глубинных уровнях иерархического строения естественных систем.
Утверждения сильной гипотезы могут принять значительно более осторожное звучание (при сохранении их эвристической роли) в случае отказа от придания обменному движению и течению времени онтологического статуса: обменные представления о движении (“вход” и “выход” точек пространства в движущийся объект) можно рассматривать лишь как удобный прием описания движения.
Эталонный объект — часы — начинает играть роль эталонной линейки, как только делегировавший его уровень в результате конвенции становится “пространственным” измерением. Интервал времени в этом случае превращается в интервал расстояния.
Следует отметить, что в метаболической конструкции пространство с необходимостью представляет собой материальную субстанцию, среду. Правда, эта среда по отношению к движущимся в ней объектам ведет себя совершенно непохоже на эфир XIX века: движущимся телам не приходится ни “раздвигать” частицы среды, испытывая ее сопротивление (т.е. “эфирного ветра” не существует), ни увлекать среду в движение за собой; поскольку по отношению к предчастицам обобщенное (субституционное) движение объектов происходит путем замены предэлементов в объектах, при этом не возникает ни сопротивления движению, ни увлечения предчастиц.
Свойства и уравнения субституционного движения. Конструкция времени, как указывалось во введении книги, должна служить одним из существенных компонентов построения динамической теории. Приведу иллюстрацию возможных путей разработки компонентов такой теории на основе метаболической конструкции. Подчеркну, что речь идет лишь об иллюстрации подходов и об исследовательской программе, но не о законченной разработке.
В качестве элементарного объекта теории рассмотрим иерархический объект, изменчивость которого задается генеральными процессами на уровнях его строения. В рамках построения I-компонента теории (см. раздел “Время — компонент теоретического знания” во втором параграфе введения) уровень элементов этого объекта интерпретирую как пространственное измерение нашей модельной физической системы, а уровень предэлементов — как субстанциональный референт координатного времени системы. Количество элементов нашего объекта интерпретирую как энергетическую его характеристику — функцию Лагранжа L, а количество предэлементов — как импульс системы p. В табл. 1 представлены постулаты, вводящие связь между количествами замененных в системе элементов или предэлементов и изменениями ее только что введенных физических характеристик. Напомню, что Dl+ есть количество вошедших в выделенную систему частиц и Dl- — количество частиц, вышедших из нее. Замечу, что движение на уровне элементов всегда есть и движение на уровне предэлементов, поскольку вместе с заменяемыми элементами меняются и содержащиеся в них предэлементы, но не наоборот.
Таблица 1
Физическая интерпретация теоретико-системных понятий
|
Теория систем |
Естествознание |
|
Объект |
Физическая система |
|
Уровень элементов |
|
|
Количество элементов, n |
Функция Лагранжа системы, L |
|
Изменение количества элементов в системе |
Изменение функции Лагранжа DL =Dn+-Dn- |
|
Количество менявшихся в системе элементов |
Перемещение в пространстве Dx =Dn+ +Dn- |
|
Уровень предэлементов |
|
|
Количество предэлементов, m |
Импульс системы, p |
|
Изменение количества предэлементов в системе |
Изменение импульса Dp =Dm+-Dm- |
|
Количество менявшихся в системе предэлементов |
Течение времени Dt =Dm++Dm- |
Теорема о среднем 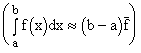 позволяет представить изменение предэлементов в объекте следующим образом:
позволяет представить изменение предэлементов в объекте следующим образом:
Dm=![]() n+
n+![]() Dn+
Dn+![]() Dn.
Dn.
Эта формула, в свою очередь, влечет соотношение
![]()
где  и
и  , которое можно назвать теоремой динамики метаболического объекта, связывающей скорость изменения импульса системы Dp/Dt с действующей на нее “силой” DL/Dx. Теорема динамики задает L-компонент динамической теории субституционного объекта.
, которое можно назвать теоремой динамики метаболического объекта, связывающей скорость изменения импульса системы Dp/Dt с действующей на нее “силой” DL/Dx. Теорема динамики задает L-компонент динамической теории субституционного объекта.
Скорость объекта v =Dx/Dt оказывается равной величине ![]() , а если движение объекта таково, что в нем меняются элементы, но предэлементы в элементах неизменны (формально: Dn+ и (или) Dn-¹
0, но Dm+ =Dm-=0), то
, а если движение объекта таково, что в нем меняются элементы, но предэлементы в элементах неизменны (формально: Dn+ и (или) Dn-¹
0, но Dm+ =Dm-=0), то ![]() , где
, где ![]() — среднее (в смысле:
— среднее (в смысле:  ) число предэлементов в элементах.
) число предэлементов в элементах.
Движение метаболического объекта обладает следующими свойствами:
- Поскольку ![]() ¹
¥
, то v ¹
0, т.е. метаболический объект обладает свойством “нелокальности”. Для каждого универсума типа i существует характерная скорость
¹
¥
, то v ¹
0, т.е. метаболический объект обладает свойством “нелокальности”. Для каждого универсума типа i существует характерная скорость ![]() средн.
средн.![]() , где N.i — число элементов в универсуме типа i.
, где N.i — число элементов в универсуме типа i.
- Существует максимально возможная скорость метаболического движения в среде каждого из универсумов. Этой скоростью обладают объекты, состоящие из “однопредэлементных” (![]() =1) элементов.
=1) элементов.
- В линейном приближении выполняется теорема сложения скоростей. А именно, пусть элементы среды, содержащие в среднем по ![]() предэлементов, при попадании в объект меняют “наполнение” на
предэлементов, при попадании в объект меняют “наполнение” на ![]() предэлементов, т.е. объект теряет скорость относительно среды. Скорость объекта есть
предэлементов, т.е. объект теряет скорость относительно среды. Скорость объекта есть  . При
. При  выполняется
выполняется  = =vср.-u, где u = a vср., или u = vср. - vоб., т.е. относительная скорость может быть представлена алгебраической суммой скоростей.
= =vср.-u, где u = a vср., или u = vср. - vоб., т.е. относительная скорость может быть представлена алгебраической суммой скоростей.
- Назовем движение с ![]() и
и ![]() равновесным (ни предэлементы в элементах, ни элементы в объекте не накапливаются и не истощаются). При равновесном движении действующая на объект сила
равновесным (ни предэлементы в элементах, ни элементы в объекте не накапливаются и не истощаются). При равновесном движении действующая на объект сила ![]() равна нулю и импульс постоянен (теорема инерции).
равна нулю и импульс постоянен (теорема инерции).
- Равновесное движение не может быть обнаружено при помощи измерения величин DL и Dp, тождественно равных нулю при любых равновесных движениях (теорема относительности равновесного движения).
- При движении с Dn+ = Dn- = 0 функция Лагранжа системы не меняется, скорость равна нулю, но скорость изменения импульса объекта определяется изменениями предэлементов в его элементах:
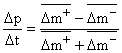 .
.
- Определим обращение субституционного движения следующими преобразованиями:
![]() и
и ![]() .
.
Уравнение субституционного движения инвариантно к обращению движения (теорема обращения движения). Замечу, что “обращение времени” (![]() и
и ![]() и, следовательно,
и, следовательно, ![]() ) не оставляет инвариантным уравнение динамики, но сохраняет уравнение Ньютона (см. следующее свойство).
) не оставляет инвариантным уравнение динамики, но сохраняет уравнение Ньютона (см. следующее свойство).
- Для “одноуровневого” движения (Dn+ и (или) Dn-¹
0, но ![]() ) уравнение динамики субституционного движения
) уравнение динамики субституционного движения ![]() переходит в уравнение динамики Ньютона
переходит в уравнение динамики Ньютона ![]() .
.
- В случае неинтенсивных замен предэлементов в элементах, точнее, при a, b << 1, уравнение динамики в линейном приближении приобретает вид:
![]() .
.
Поскольку a, b ~ 1/![]() ~ v, то оказывается, что при определенных скоростях движения субституционного объекта появляются дополнительные к ньютоновским силы, пропорциональные этим скоростям и самим силам (например, при
~ v, то оказывается, что при определенных скоростях движения субституционного объекта появляются дополнительные к ньютоновским силы, пропорциональные этим скоростям и самим силам (например, при![]() =
=![]() º
º
![]() оказывается
оказывается ![]() ). При этом уравнение движения не инвариантно к “обращению времени”. Экспериментальные интерпретации существования дополнительных сил обсуждаются во втором томе настоящей книги.
). При этом уравнение движения не инвариантно к “обращению времени”. Экспериментальные интерпретации существования дополнительных сил обсуждаются во втором томе настоящей книги.
- Пусть, кроме уровней элементов и предэлементов, рассматривается и предшествующий им уровень предчастиц. Пусть для предчастиц l определены изменения “координаты” Dt=Dl++Dl- и “функции” DG = Dl+-Dl-. Уравнение динамики легко обобщается на случай движения с учетом замены предчастиц:
![]() ;
;
![]()
где поправки a, b, c, d и др. оценивают интенсивности “внутренних” движений в элементах по сравнению с интенсивностью перемещения объекта на уровне элементов.
1.4. Трудности субституционного подхода
1. При наличии нескольких сортов составляющих систему элементов нужны дополнительные соображения для выбора сорта частиц или комбинации сортов, определяющих шкалу собственного времени. Аналогичный вопрос возникает, если система состоит из нескольких подсистем, замены элементов в которых не синхронизированы.
Жизнедеятельность клетки связана с заменами молекул многих химических элементов, скорость обмена которых весьма различна. В качестве метаболических часов клетки может быть выбран так называемый “лимитирующий” элемент или сумма молекул всех сортов, что удобно в одних и не подходит для других случаев.
Клетки организма дифференцированы, и скорости замены клеток различных тканей, подсистем или органов неодинаковы. Таким образом, замены каких клеток — эпителиальных, нейронов или эритроцитов — отсчитывают биологический возраст животного?
Структурированность естественных систем обязывает и в качестве формального их описания использовать множества с заданными на них математическими структурами (отношениями, операциями, топологиями...). Метаболический подход подразумевает умение подсчитывать количество элементов в объектах. Поэтому при использования метаболической конструкции для множеств со структурой требуется обобщение на них понятия “количество элементов”.
2. В метаболическом подходе есть свой элементарный объект, пространство состояний, способ идеализации изменчивости и ее количественная параметризация, но не сформулирован принцип для выявления закона изменчивости систем (уравнение метаболического движения, полученное в предыдущем разделе, основано на догадке, а не на систематическом правиле вывода).
3. Метаболическая конструкция подразумевает умение фиксировать принадлежность элементов объектам, а также умение подсчитывать количество элементов в объектах и обнаруживать его изменение. Математическая теория множеств начинается с момента, когда вопрос о принадлежности или непринадлежности элементов множеству уже решен. В естествознании же необходима операциональная процедура, обеспечивающая практическую или принципиальную возможность решения вопроса о принадлежности. И теория должна базироваться на аксиоматике, допускающей неаприорное использование представлений о принадлежности. Умение подсчитывать количество элементов в множествах обеспечивается существованием однозначных или неоднозначных отображений между множествами. И если в математической теории такие отображения должны существовать в принципе, то в естественнонаучных интерпретациях их существование должно обеспечиваться операционально-экспериментальными процедурами. Конструирование необходимых процедур, возможно, лежит на пути обобщения естественнонаучного понятия “сигнала”.
4. Принцип изменчивости задает конструкцию событий как акты замены элементов системы. При этом требуется дополнительный постулат, вводящий отношение порядка на совокупности событий. Необходимый принцип упорядочения неявно вводится выбором эталонного объекта: оказывается, что для любого эталона времени замены элементов (точнее, совокупностей одновременно заменяемых элементов) упорядочены в нашем опыте. В метаболическом подходе пока нет конструкций, позволяющих естественно ввести принцип упорядочения.
В следующих разделах предлагаются пути преодоления некоторых из указанных трудностей.
§2. Энтропийная параметризация времени
и экстремальный принцип движения
Все реальные системы при формальном описании эксплицируются структурированными множествами, поэтому применение метаболического подхода требует научиться подсчитывать количество замененных элементов во множествах со структурой.
2.1. Количество элементов структурированных множеств
Категории вместо множеств. Применение математического формализма в теоретическом знании начинается с подбора в качестве элементарного объекта теории определенным образом структурированного множества.
Экологическое сообщество из особей различных видов удобно описывать структурой множества с разбиениями, где классы соответствуют слагающим сообщество популяциям.
Понятие близости-удаленности точек в эмпирическом пространстве описывается топологической математической структурой.
Совокупность состояний атома можно описать векторами бесконечномерного гильбертова пространства или равносильным образом — полем бесконечных матриц.
В математике создан язык для описания произвольных структурированных множеств — теория категорий и функторов. Элементарным конструктом теории категорий является не “застывшее” состояние естественного объекта (каким предстает объект в теории множеств), а преобразование, “движение” объекта, на языке теории категорий — морфизм. Категория — понятие более общее, чем множество: только некоторые из категорий при определенных условиях становятся совокупностями множеств.
Мощности вместо количеств. Последовательное изложение представлений о кардинальной структуре множеств и возможных ее обобщениях содержится в книге, специально посвященной естественнонаучным приложениям теории категорий (Левич, 1982), там же доказываются все утверждения, на которые опирается дальнейшее, по возможности неформализованное, изложение.
Есть два способа сравнить количество элементов в множествах. Пусть нам, к примеру, необходимо выяснить, хватит ли стульев для оказавшейся в комнате группы людей. Можно подсчитать отдельно количество стульев, отдельно — количество людей и сравнить два получившихся числа. Можно же попросить, чтобы каждый человек в одиночку сел на один стул. После того как все люди усядутся, мы, не зная ни количества стульев в комнате, ни количества людей, тем не менее точно сможем сказать, какое из этих количеств больше: в зависимости от того, останутся ли свободными стулья или — стоящими люди. В математике такой способ сравнения множеств называется установлением соответствия (отображения) между множествами. Второй способ сравнения количеств фундаментальнее первого: конструкция числа элементов строится на основе установления соответствий между множествами.
Будем задавать соответствие между элементами множеств стрелками. Если из каждого элемента множества A выходит единственная стрелка и к элементам множества B приходит не более, чем одна стрелка (рис.3), то такое соответствие из A в B называется инъекцией. Когда существует инъекция из A в B (на каждом стуле сидит один человек и никто не занял несколько стульев сразу), мы говорим, что количество элементов в множестве A меньше или равно количеству элементов в множестве B. Если существует инъекция как из A в B, так и из B в A, то количество элементов в этих множествах одинаково. Поскольку с помощью соответствий можно сравнивать не только конечные, но и бесконечные множества, вместо термина “одинаковое количество элементов” используют термин “равномощность” и термин “мощность” — вместо понятия “количество элементов”. Натуральные числа — мощности конечных множеств — становятся названиями соответствующих классов равномощных друг другу совокупностей.
Сила структур. Приведу примеры структурированных множеств.

1) Множества с разбиениями. Указываются признаки элементов множества, по которым их следует считать эквивалентными. Группы эквивалентных элементов образуют непересекающиеся классы, на которые разбивается исходное множество.
Сообщество живых организмов, принадлежащих одному местообитанию, например, все особи пруда, по целому набору признаков разделяются на популяции организмов, принадлежащих одному биологическому виду.
Множество натуральных чисел разбивается на классы чисел, дающих при делении, например, на 3, одинаковый остаток: N = k0 È k1 È k2, где k0 = {3, 6, 9, 12, ...}, k1 = {1, 4, 7, 10, ...} и k2 = {2, 5, 8, 11, ...}.
2) Множество с законами композиции. Для любых двух элементов a и b этого множества определен третий элемент c, называемый их композицией.
В множестве целых чисел для двух любых элементов определен третий — их сумма.
В алгебре логики с двузначным пространством истинности {истина (и), ложь (л)} определен ряд логических операций (законов композиции). Например,
|
конъюнкция: |
Ù |
и |
л |
или дизъюнкция: |
Ú |
и |
л |
|
и |
и |
л |
и |
и |
и |
||
|
л |
л |
л |
л |
и |
л |
3) Метрические пространства. Для любых двух элементов a и b определено число S (a, b) такое, что S(a, a) = 0, S (a, b) = S (b, a) и S (a, c) £ S (a, b) + S (b, c).
Для точек ![]() и
и ![]() в трехмерном евклидовом пространстве определено S(
в трехмерном евклидовом пространстве определено S(![]() ,
, ![]() ) =
) = ![]() .
.
Для структурированных множеств из всех возможных соответствий выделены те, которые сохраняют структуру множества. Эти соответствия называют морфизмами структуры.

Для экологического сообщества морфизмами, сохраняющими разбиение на виды, будут преобразования, состоящие в рождении или смерти особей. При этих преобразованиях биологический вид переходит в себя.
Для произвольных множеств с разбиениями по определению морфизмами служат соответствия, не перемешивающие классы эквивалентных элементов. Так, для отношения делимости чисел морфизмом будет числовая функция, заключающаяся в умножении на любое натуральное число y=n x (например, если x1 и x2 имели одинаковый остаток при делении на 3, то соответствующие y1 и y2 будут также иметь одинаковый остаток).
Для закона сложения целых чисел морфизмом будет, например, преобразование, состоящее в замене знака числа y Þ -x: a + b = c Þ -a+(-b)=-c.
Одним из морфизмов метрической структуры является преобразование вращения в пространстве — вращения сохраняют метрику пространства.
Количественное сравнение между собой неструктурированных множеств легко обобщить на множества, обладающие одинаковыми структурами. Структура множества A считается слабее структуры множества B, если существует инъективный морфизм структуры из A в B. Например, разбиение множества A на рис.4 оказывается слабее разбиения множества B.

Так же как сравнение с помощью инъекций неструктурированных множеств порождает понятие количества элементов во множестве (натуральные числа, мощности), так и сравнение структурированных множеств с помощью морфизмов порождает структурные числа структурированных множеств. По количеству элементов мы можем сравнивать любые множества, так как для любых двух множеств выполняется принцип трихотомии: количество элементов в A меньше, чем в B; или количество элементов в A больше, чем в B; или количество элементов в A равно количеству элементов в B. Т.е. всегда существует инъекция или из A в B, или из B в A, или и та и другая. По структурным числам структурированные множества упорядочены лишь частично — существуют пары структурированных множеств, для которых ни прямой, ни обратной инъекций, сохраняющих структуру, не существует. На рис.5 приведен пример множеств с разбиениями, между которыми нет инъективных морфизмов. Так что если структурные числа положить в основу параметризации изменчивости, то получающееся таким образом время будет выглядеть экзотически: его моменты упорядочены не линейно, а лишь частично.
Функторное сравнение структур. Частичная упорядоченность структурных чисел и возникающая порой техническая трудность обнаружения инъективных морфизмов для некоторых структур заставляют продолжить поиск путей количественного сравнения структурированных множеств. Путь, на котором поиск мог бы оказаться удачным, хорошо разработан в математике. Речь идет о представлении одних математических структур другими математическими структурами.
Свойства вращения геометрического пространства можно эффективно изучать с помощью умножения определенных матриц.
Вся теория меры, в частности, измерение длин, площадей и объемов в геометрии есть пример количественной параметризации, основанной на представлении геометрических структур в числовые структуры анализа.
Равносильные математические описания нередки в физике: состояния атома в квантовой механике могут описываться векторами бесконечномерного гильбертова пространства (подход Шредингера) и бесконечными матрицами (подход Гейзенберга).
Поскольку в интересующем нас аспекте — при количественном сравнении одинаково структурированных множеств — нам приходится иметь дело не только с самими структурированными множествами, но и в большой степени с морфизмами их структуры, дальнейшее изложение удобно вести на языке математической теории категорий, который специально предназначен для изучения совокупностей, куда на равных правах входят структурированные множества и их морфизмы.
Категория включает класс объектов и множества морфизмов, заданных для некоторых (или всех) пар объектов. Для морфизмов заданы закон композиции и ряд аксиом, делающие морфизмы похожими на математические соответствия между множествами. Наиболее наглядные примеры категорий — это совокупности всех одинаково структурированных множеств:
- в категории упорядоченных множеств, где объекты — множества с отношением порядка, морфизмами служат монотонные (возрастающие и убывающие) соответствия между множествами;
- в категории групп морфизмы между объектами категории — группами — есть соответствия, сохраняющие закон композиции и единичные элементы групп;
- в категории топологических пространств, где объекты — множества, для элементов которых задано отношение близости, морфизмы есть непрерывные соответствия, переводящие близкие элементы одного топологического пространства в близкие элементы другого пространства;
- среди всевозможных категорий присутствует и категория всех множеств, объекты категории — множества, морфизмы — соответствия между множествами.
Функтор — это отображение одной категории в другую, при котором объекты переходят в объекты, морфизмы — в морфизмы и обязательно сохраняется композиция морфизмов. Функторы оказываются представлением структур одной категории структурами другой.
Выделенные морфизмы категорий порождают упорядочение ее объектов. Так, в предыдущих абзацах мы сравниваем структурированные множества с помощью инъективных морфизмов. Если функторное представление монотонно относительно упорядочения в категориях (“структура объекта A сильнее структуры объекта B в категории S1” влечет “структура объекта F(A) сильнее структуры объекта F(B) в категории S2”, где F — функтор из S1 в S2), то предъявление монотонного функтора составляет функторный метод сравнения структур: об упорядочении объектов A и B в какой-либо категории со сложной и непривычной структурой можно судить по упорядочению их образов F(A) и F(B) в категории с простой или хорошо изученной структурой объектов (в цитированной выше книге (Левич, 1982) приведены достаточные условия монотонности функтора).
Инварианты структур. Функтор из произвольной категории структурированных множеств в категорию неструктурированных множеств, сопоставляющий объекту A множество всех морфизмов Hom(X, A) из фиксированного объекта X в объект A, оказывается монотонным при упорядочении структурированных множеств инъекциями. Таким образом, если структура объекта A сильнее структуры объекта B, то количество сохраняющих структуру преобразований произвольного объекта X в объект A больше, чем количество таких же преобразований из объекта X в объект B. Если структуры объектов A и B одинаковы, то количества преобразований в множествах Hom (X, A) и Hom(X, B) равны. Поэтому число преобразований в множестве Hom(X, A) удобно назвать инвариантом структуры объекта A относительно объекта X и обозначить ![]() (A).
(A).
Заметим, что если ![]() есть инварианты объекта A для нескольких X, то и сумма
есть инварианты объекта A для нескольких X, то и сумма ![]() обладает свойcтвами инварианта.
обладает свойcтвами инварианта.
Если структурированные объекты сравнимы, то их инварианты упорядочены так же, как объекты. Однако мы знаем, что структурированные множества могут оказаться несравнимыми. В этом случае может быть полезным принцип продолжения упорядочения структур по упорядочению их инвариантов: структура объекта A полагается сильнее (относительно объекта X) структуры объекта B, если IX(A) ³ IX(B).
Функторное сравнение структур можно рассматривать как дальнейшее обобщение понятия количества: от количества элементов бесструктурных множеств (задаваемого сравнением множеств с помощью инъекций) через структурные числа структурированных множеств (задаваемые сравнением множеств с помощью инъективных морфизмов структур) к числовым инвариантам структур. По-видимому, приведенные конструкции — не единственный путь обобщения представлений о количестве (см. Шаров, 1977). Возможен путь поиска иных функторов в категорию множеств, или выбор иной параметризирующей категории вместо категории множеств, или выбор вместо инъекций других специальных морфизмов для сравнения объектов в исходной категории (и соответственно — иного функтора в параметризирующую категорию) и т.д.
Приведу пример сравнения структур с помощью инвариантов. Рассмотрим структуру множеств с разбиениями. Допустимыми служат морфизмы, переводящие каждый класс разбиения одного множества целиком в определенный единственный класс другого множества. Если ![]() — класс i разбиения множества X,
— класс i разбиения множества X, ![]() — класс разбиения множества A, в который переходит класс i, то общее количество морфизмов есть
— класс разбиения множества A, в который переходит класс i, то общее количество морфизмов есть
![]() .
.
Если морфизмы — отображения и в классе Ki содержится ni элементов, то
![]() .
.
Если допустимыми являются не отображения класса в класс, а какие-либо произвольные соответствия из класса в класс, то формула инварианта сохраняет вид произведения по классам с измененными сомножителями. Приведу формулы для сомножителей при всех возможных комбинациях канонических свойств соответствий (табл.2).
Замечу, что инварианты многих (а может быть, и произвольных) математических структур выражаются через ассоциированные с этими структурами разбиения, поэтому их инварианты имеют характерный вид произведения инвариантов отдельных классов разбиения. Это замечание пригодится при обсуждении способов расчета энтропии систем.
2.2. Категорное описание систем
O-, C- и S-компоненты теории. Пусть для описания естественной системы выбрана определенная математическая структура, пусть также из содержательных соображений известны допустимые структурой системы преобразования. Рассмотрим категорию Q структурированных множеств, где математическая структура, заданная на множествах, эксплицирует свойства системы.
Станем отождествлять состояния системы с объектами категории, а преобразования состояний друг в друга — с ее морфизмами. На языке методологии теоретического описания естественных систем (см. введение книги) элементарный объект теории теперь есть структурированное множество; изменчивость системы — морфизмы категории, преобразующие одни объекты в другие; пространство состояний — совокупность объектов категории Q.
Таблица 2
Количество соответствий из множества X (с количеством элементов x) в множество A (с количеством элементов a). Ck означает множество C с количеством элементов в нем k. Нижние индексы означают, что подсчитывается количество соответствий, обладающих теми свойствами, обозначения которых вошли в индексы:
p — всюду определенные соответствия;
f — функциональные соответствия;
i — инъективные соответствия;
s — сюръективные соответствия.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечу, что теоретико-категорное описание систем не требует обязательной экспликации естественной системы математической структурой. Возможно “качественное” категорное описание систем, т.е. перечисление и описание состояний системы, а также всех переходов между состояниями (морфизмов) не на математическом, а на каком-либо внутридисциплинарном языке.
Для формулировки полной динамической теории осталось задать ее T и L компоненты — способ параметризации изменчивости и закон изменчивости.
Энтропия систем. Введу энтропию состояния A относительно состояния X через инварианты структурированных множеств следующим образом:
 . (2.1)
. (2.1)
Здесь Q — категория структурированных множеств, а ![]() — категория множеств со “стертой структурой”. X маркирует состояния системы, принадлежащие определенному ее макросостоянию (понятие макросостояния вводится в последующих абзацах). Энтропия всего макросостояния определяется надлежащим суммированием по всем X.
— категория множеств со “стертой структурой”. X маркирует состояния системы, принадлежащие определенному ее макросостоянию (понятие макросостояния вводится в последующих абзацах). Энтропия всего макросостояния определяется надлежащим суммированием по всем X.
Формулу (2.1) для энтропии можно интерпретировать как меру структурированности состояния A, т.е. меру отклонения структуры состояния A от его бесструктурного аналога.
Эта формула обобщает традиционные подходы к введению энтропии в статистической физике. Обычно энтропия систем определяется как логарифм удельного числа различающихся микросостояний системы, соответствующих ее заданному макросостоянию. Буду интерпретировать макросостояние как класс состояний, между которыми допустимы переходы с точки зрения каких-либо содержательных соображений, например, в силу сохранения макропараметров системы (энергии, числа частиц...), а микросостояние как результат произвольного преобразования системы.
Таким образом, чтобы вычислить энтропию системы, нужно подсчитать количество ее преобразований-морфизмов ![]() . Это количество морфизмов зависит как от структуры системы, так и от количества элементов в ней. Множитель
. Это количество морфизмов зависит как от структуры системы, так и от количества элементов в ней. Множитель ![]() введен, чтобы нормировать энтропию на один элемент системы, или ввести удельный инвариант структуры.
введен, чтобы нормировать энтропию на один элемент системы, или ввести удельный инвариант структуры.
“Энтропиевидные” функции состояния систем, появившись в термодинамике, через статистическую физику, теорию информации и кибернетику проникли в количественные методы широкого круга наук. Успешность применения понятия энтропии полностью определяется возможностями расчета энтропии в интересующих исследователя случаях. Чисто термодинамические подходы к расчету энтропии систем крайне ограничены: “... формулировка второго начала с точки зрения современного физика представляет собой скорее программу, чем утверждение, допускающее однозначную интерпретацию, так как ни Томпсон, ни Клаузиус не указали точный рецепт, позволяющий выразить изменение энтропии через наблюдаемые величины” (Пригожин, 1985, с.93). И только больцмановская интерпретация энтропии через число способов достижения системой макросостояния дает конструктивные способы для расчетов. Интерпретация энтропии через количество морфизмов предоставляет дальнейшие возможности для расчетов.
Как уже говорилось, инварианты многих (если не всех) математических структур выражаются через инварианты ассоциированных со структурами разбиений. Инварианты множеств с разбиениями мультипликативны относительно инвариантов каждого из классов разбиения, поэтому логарифмы инвариантов, входящие в энтропию, аддитивны и имеют характерный “энтропиеобразный” вид сумм по классам разбиения.
Формулы для энтропии получаются вне каких-либо статистических предпосылок. Например, если допустимые морфизмы есть отображения, то формула
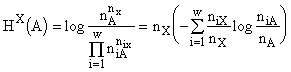 ,
,
где ![]() и
и ![]() , справедлива при любых, пусть самых малых, n. Вводя pi =ni/n и представляя набор величин как функцию распределения для состояния A, можно формулу для энтропии интерпретировать как обобщение H-функции Больцмана
, справедлива при любых, пусть самых малых, n. Вводя pi =ni/n и представляя набор величин как функцию распределения для состояния A, можно формулу для энтропии интерпретировать как обобщение H-функции Больцмана
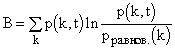 ,
,
которая (Пригожин, 1985, с.303) служит мерой отклонения вероятностей состояния системы в момент t от вероятностей равновесного состояния.
Заметим, что приведенные в настоящем разделе в качестве примеров формулы энтропии (так же как и обобщающие энтропию формулы инвариантов в табл.2) относятся к простейшим — двухуровневым системам. В задачах, где оказывается существенным большее количество иерархических уровней системы, возникает необходимость расчета инвариантов для иерархических структур (например, структуры армад; Левич, 1982).
2.3. Экстремальный принцип как закон изменчивости
Уравнение движения в естествознании — это обычно постулат, обобщающий опыт математического описания определенного фрагмента реальности, и изобретенный гением, чье имя становится именем уравнения. Существует и иной путь получения уравнений: постулат-уравнение заменяется постулатом-функционалом. Речь идет об экстремальных принципах естествознания, согласно которым в реальности осуществляются те состояния системы, для которых экстремальна определенная числовая функция (функционал), аргумент которой — нужные исследователю траектории движения системы.
Если известно уравнение движения, то по нему можно установить вид функционала, экстремалью которого будет решение исходного уравнения. И наоборот, если функционал задан, то вариационный метод поиска его экстремумов приводит к уравнениям движения. Так что построение динамики на основе постулатов-уравнений или постулатов-функционалов приводит к одинаковым результатам. Однако экстремальный принцип обладает большей эвристической и обобщающей силой.
Почему камень, брошенный под углом к горизонту, движется по параболе? Объясняя явление, можно указать на уравнение равнопеременного движения ![]() . Само это уравнение составляет следствие второго закона Ньютона
. Само это уравнение составляет следствие второго закона Ньютона ![]() для тела, движущегося под действием постоянной силы (впрочем, парабола может быть представлена геодезической линией — решением уравнений Эйнштейна общей теории относительности для движения в сильных полях и с высокими скоростями). Закон Ньютона и уравнения Эйнштейна могут быть выведены из принципа наименьшего действия с определенной формой экстремизируемого лагранжиана, т.е. существует несколько уровней объяснения явлений, каждый из которых может служить исходным постулатом. Однако уравнение равнопеременного движения относится лишь к узкому классу явлений, второй закон Ньютона описывает все движения в несильных полях и с невысокими скоростями, уравнения Эйнштейна уже не связаны и с этими ограничениями, а принцип наименьшего действия применим ко всем формам механического и электромагнитного движений.
для тела, движущегося под действием постоянной силы (впрочем, парабола может быть представлена геодезической линией — решением уравнений Эйнштейна общей теории относительности для движения в сильных полях и с высокими скоростями). Закон Ньютона и уравнения Эйнштейна могут быть выведены из принципа наименьшего действия с определенной формой экстремизируемого лагранжиана, т.е. существует несколько уровней объяснения явлений, каждый из которых может служить исходным постулатом. Однако уравнение равнопеременного движения относится лишь к узкому классу явлений, второй закон Ньютона описывает все движения в несильных полях и с невысокими скоростями, уравнения Эйнштейна уже не связаны и с этими ограничениями, а принцип наименьшего действия применим ко всем формам механического и электромагнитного движений.
Экстремальный принцип. Для естественных систем, описываемых математическими структурами, предлагается экстремальный принцип в следующей форме: из заданного состояния X системы осуществляется переход в то состояние A, для которого энтропия HX(A) максимальна в пределах, допускаемых ограничениями на функционирование системы (например, доступной энергией или другими ресурсами).
Таким образом, на языке категорного описания систем возникает L-компонент теории.
В обсуждаемом контексте энтропия — не исходное и неопределяемое понятие, а точная конструкция. Это позволяет предложить для экстремального принципа дополнительные варианты интерпретаций.
1. По определению энтропия HX(A) рассматривается как мера удаленности структурированного состояния A из категории Q от своего аналога из категории ![]() со “стертой” структурой. И согласно экстремальному принципу осуществляются состояния, которые сильнее других удалены от своего полностью бесструктурного прообраза (максимально структурированы).
со “стертой” структурой. И согласно экстремальному принципу осуществляются состояния, которые сильнее других удалены от своего полностью бесструктурного прообраза (максимально структурированы).
2. В формуле энтропии знаменатель ![]() есть инвариант структурированного множества A. Неравенство
есть инвариант структурированного множества A. Неравенство ![]() означает, что структура множества A слабее (по отношению к объекту X) структуры множества B в смысле отношения порядка “сила структур”. Пусть для состояний системы A и B числители
означает, что структура множества A слабее (по отношению к объекту X) структуры множества B в смысле отношения порядка “сила структур”. Пусть для состояний системы A и B числители ![]() в формуле энтропии одинаковы, т.е. состояния A и B являются различными реализациями некоторой структуры на одинаковых по мощности базовых множествах, например, различными разбиениями одного и того же множества или группами, равномощными как множества. Тогда максимум энтропии и реальное состояние соответствуют минимальному (по “силе структур”) состоянию системы. Таким образом, энтропия играет ту же роль, что и инварианты математических структур, упорядочивая сами структуры и описываемые математическими структурами состояния естественных систем.
в формуле энтропии одинаковы, т.е. состояния A и B являются различными реализациями некоторой структуры на одинаковых по мощности базовых множествах, например, различными разбиениями одного и того же множества или группами, равномощными как множества. Тогда максимум энтропии и реальное состояние соответствуют минимальному (по “силе структур”) состоянию системы. Таким образом, энтропия играет ту же роль, что и инварианты математических структур, упорядочивая сами структуры и описываемые математическими структурами состояния естественных систем.
3. На примере энтропии структуры множеств с разбиениями (морфизмы — биекции) видно, что энтропия  максимальна при одновременном выполнении двух условий: количество элементов системы (числитель) максимально, но число всех сохраняющих структуру преобразований (знаменатель) минимально. Малый набор допустимых структурой системы преобразований можно трактовать как высокую устойчивость состояния, и экстремальный принцип реализует как максимум экспансии элементов системы, так и максимально устойчивое ее состояние.
максимальна при одновременном выполнении двух условий: количество элементов системы (числитель) максимально, но число всех сохраняющих структуру преобразований (знаменатель) минимально. Малый набор допустимых структурой системы преобразований можно трактовать как высокую устойчивость состояния, и экстремальный принцип реализует как максимум экспансии элементов системы, так и максимально устойчивое ее состояние.
4. Заметим, что без дополнительных ограничений требование наибольшей экспансии, порождаемое экстремальным принципом, приводит к бесконечному увеличению числа элементов системы. Функционирование естественных систем всегда ограничено ресурсами (энергия, субстраты, пространство, информация и т.д.). Например, для субстратно-энергетических факторов эти ограничения формализуются в виде балансовых неравенств:
![]() , (2.2)
, (2.2)
где ![]() — некоторые функции состояния системы и
— некоторые функции состояния системы и ![]() — потребляемые системой при экспансии различные ресурсы. Поэтому реальными состояниями системы являются решения задачи на условный экстремум.
— потребляемые системой при экспансии различные ресурсы. Поэтому реальными состояниями системы являются решения задачи на условный экстремум.
Можно показать, что энтропийный экстремальный принцип с ограничениями (2.2) по ресурсным факторам равносилен принципу минимального потребления любого из лимитирующих динамику ресурсных факторов с ограничениями на наименьшую допустимую величину энтропийной характеристики системы.
5. Обе указанные выше вариационнные задачи равносильны задаче на безусловный экстремум (для функции Лагранжа, одинаковой для обеих задач). Например, задача {Энтропия H(A) — максимальна, ![]() , где E — энергия системы} равносильна задаче на безусловный минимум для функционала F = -(H + dE), где d — множитель Лагранжа. Заметим, что в статистической физике для идеальных газов множитель Лагранжа оказывается обратно пропорциональным температуре d = - 1/T и справедливо F = (E -T H) 1/T. В такой ситуации экстремальный принцип трактуется как принцип минимума свободной энергии системы.
, где E — энергия системы} равносильна задаче на безусловный минимум для функционала F = -(H + dE), где d — множитель Лагранжа. Заметим, что в статистической физике для идеальных газов множитель Лагранжа оказывается обратно пропорциональным температуре d = - 1/T и справедливо F = (E -T H) 1/T. В такой ситуации экстремальный принцип трактуется как принцип минимума свободной энергии системы.
6. Энтропию системы, выраженную через инварианты соответствующих математических структур, можно рассматривать как количество информации, связанной со структурой системы (Левич, 1978), поэтому введенный экстремальный принцип можно интерпретировать и в информационных терминах.
В дальнейшем изложении обсуждены и другие интерпретации экстремального принципа: максимум экологического разнообразия, сопоставление со вторым началом термодинамики, аспекты возрастания сложности и самоорганизации систем.
Следует ли принцип экстремальности энтропии непременно интерпретировать лишь как возможность возрастания энтропии к максимуму? Г.Е.Михайловский (1988) выделяет мир существующего (мир Лапласа) со стационарным значением энтропии, мир возникающего (мир Пригожина) с возрастающей в силу динамической неустойчивости энтропией вдоль реальных траекторий и мир развивающегося (мир действия принципа эквифинальности) с отрицательными приростами энтропии, относя существенно биологические и социальные системы только к миру эквифинальности.
Предложенный в настоящей работе принцип осуществления экстремальной структуры систем безусловно открыт для дальнейших обобщений и новых интерпретаций.
Появление энтропии в предлагаемом контексте обладает рядом особенностей по сравнению с ситуациями, в которых энтропия неоднократно возникала в различных областях естествознания:
- энтропии придается универсальная общенаучная роль функционала, порождающего законы изменчивости систем;
- энтропия приобретает смысл, аналогичный смыслу инвариантов математических структур — количественное представление, упорядочивающее состояния естественных систем, монотонное с упорядочением состояний при помощи гомоморфизмов систем; поскольку инварианты структур рассчитываются через количества допустимых преобразований, указанная трактовка энтропии оказывается обобщением больцмановского определения энтропии;
- энтропия однозначно рассматривается вне каких-либо вероятностных соображений. Величина ее зависит от эксплицирующей систему математической структуры и допустимых системой преобразований.
2.4. Пример: формула видовой структуры в экологии сообществ
Опишем экологическое сообщество структурой множеств с разбиениями: элементы множеств — это особи, классы разбиения — популяции биологических видов. Состояние сообщества — вектор ![]() , составляющие ni которого есть численности каждого из w слагающих сообщество видов.
, составляющие ni которого есть численности каждого из w слагающих сообщество видов.
На рис.6 представлены преобразования, происходящие с биологическими организмами, и их математическая интерпретация.
Конкретизируем модель для сообщества организмов одного трофического уровня, например, для фитопланктонного сообщества без интродукции клеток извне. Для фитопланктона отсутствует поглощение одних клеток другими и слияние особей, также виды ни генетически, ни трофически не взаимодействуют друг с другом. Поэтому допустимыми преобразованиями будут необязательно всюду определенные (смертность), необязательно функциональные (деление клеток), но сюръективные (отсутствие интродукции) и инъективные (отсутствие слияния клеток) соответствия каждого класса разбиения в себя же (отсутствие взаимодействия видов).

Заметим, что модель сообщества определяется не только эксплицирующей математической структурой (множества с разбиениями), но и допустимыми морфизмами. Выбор иных морфизмов при сохранении той же структуры порождает иную модель. Так, биекции в качестве морфизмов приводят к существованию состояний сообщества лишь с постоянными численностями видов. Выбор свойств допустимых морфизмов, как проиллюстрировано ниже, совершенно меняет характер распределения численностей видов. Поэтому рассматриваемая модель является содержательно теоретико-категорной, а не только лишь использующей язык этой теории.
Функционал, максимизация которого согласно экстремальному принципу определяет динамику сообщества, для выбранных допустимых морфизмов выглядит следующим образом:
 , (2.3)
, (2.3)
где ![]() — общая численность клеток в сообществе.
— общая численность клеток в сообществе.
Заметим также, что здесь использована не локальная, а глобальная формулировка экстремального принципа: ищется финальное стационарное состояние системы, для которого экстремальна энтропия перехода лишь в самого себя, т.е. H (![]() ) = HA(A).
) = HA(A).
Сообщество функционирует за счет ресурсов среды, которые ограничивают беспредельную экспансию видов. Таким образом, реальное состояние сообщества ![]() является экстремалью вариационной задачи
является экстремалью вариационной задачи
![]() ,
,
![]() . (2.4)
. (2.4)
Здесь ![]() и
и ![]() — потребность вида i в ресурсе k, L = { L1, L2,.., Lm} и Lk — количество ресурса k, имеющееся в среде.
— потребность вида i в ресурсе k, L = { L1, L2,.., Lm} и Lk — количество ресурса k, имеющееся в среде.
Такая задача имеет решение
![]() , (2.5)
, (2.5)
где ![]() — множители Лагранжа, отыскиваемые вместе с n из системы
— множители Лагранжа, отыскиваемые вместе с n из системы
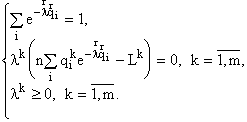 , (2.6)
, (2.6)
Заметим, что это решение единственно и обязательно существует (Левич и др., 1994).
Формула видовой структуры (2.5) позволяет адекватно описать эмпирические численности видов в экологических сообществах (Lurie, 1983; Гаврилов и др., 1986; Левич и др., 1986б; Левич и др., 1993а).
Анализ формулы (2.5) позволил (Левич и др., 1993б) сделать теоретический вывод (и подтвердить его экспериментальными исследованиями) о том, что относительная численность заданного вида принимает наибольшее значение при отношениях в среде ресурсных факторов, равных отношениям потребностей в них данного вида.
Для задачи (2.4) доказано (Левич и др., 1994) “правило лимитирующего звена”, обобщающее принцип минимума Либиха и закон совокупного действия факторов Митчерлиха: пространство потребляемых факторов среды распадается (“стратифицируется”) на 2m-1 непересекающихся подмножеств, каждому из которых соответствует единственный набор потребляемых факторов, которые (и только они) в этом подмножестве:
а) потребляются полностью;
б) являются аргументами экстремали (2.5).
Проиллюстрируем возможности метода выбором иных допустимых преобразований. Пусть допустимы произвольные соответствия, т.е., кроме смертности и размножения, допускаются интродукция особей и поглощение одних организмов другими. Решением вариационной задачи
 ,
,
![]() (2.7)
(2.7)
будет экстремаль
ni = n -![]() .
.
Заметим, что функционалы (2.4) и (2.7) применяются в экологии независимо от описываемого подхода и называются индексами разнообразия видовой структуры экологических сообществ (Левич, 1980). Таким образом, экстремальность функционала H, порождающего динамику сообщества, можно интерпретировать и как требование максимального разнообразия системы, ограниченного доступными ресурсами среды.
Следует уточнить, о какой динамике идет речь: изменчивость численности ni параметризуется количеством L потребленных сообществом субстратов. Действительно, численности ni зависят согласно (2.5) от множителей ![]() , которые согласно (2.6), как и полная численность n, являются функциями лишь потоков через сообщество ресурсов Lk, т.е. подразумевается динамика в субституционном времени системы.
, которые согласно (2.6), как и полная численность n, являются функциями лишь потоков через сообщество ресурсов Lk, т.е. подразумевается динамика в субституционном времени системы.
2.5. Время субституционное, энтропийное и категорное
Субституционное время было определено как количество замененных в системе элементов. Энтропийное время связано с количеством преобразований системы. Поскольку (согласно принципу унификации изменчивости) преобразования системы и состоят в замене элементов, то на качественном уровне связь между метаболическим и энтропийным временами очевидна. Между ними существует и однозначная количественная связь. Проиллюстрируем ее на примере вариационной задачи (2.4) предшествующего раздела. Энтропия ![]() при
при ![]() с учетом
с учетом ![]() и
и ![]() переходит в
переходит в ![]() , где множители Лагранжа
, где множители Лагранжа ![]() также зависят от L. Причем связь между энтропией и компонентами метаболического времени строго монотонна, поскольку можно показать (Левич и др., 1994), что dH/dLk ³
0.
также зависят от L. Причем связь между энтропией и компонентами метаболического времени строго монотонна, поскольку можно показать (Левич и др., 1994), что dH/dLk ³
0.
Заметим, что если один из существенных для функционирования системы факторов Lk есть тепло DQ, то соответствующий множитель Лагранжа lk есть 1/T, где T — абсолютная температура. Из этого следует, что термодинамическая энтропия DQ/T (как и больцмановская статистическая энтропия) есть частный случай категорного определения энтропии.
Формула ![]() демонстрирует важный результат: энтропия представляет собой как бы “усреднитель” метаболических времен системы с несколькими сортами заменяющихся элементов. Множители Лагранжа играют роль собственных “метаболических частот” системы. Таким образом, энтропийная параметризация разрешает возникшую в метаболическом подходе проблему разносортности элементов в универсумах.
демонстрирует важный результат: энтропия представляет собой как бы “усреднитель” метаболических времен системы с несколькими сортами заменяющихся элементов. Множители Лагранжа играют роль собственных “метаболических частот” системы. Таким образом, энтропийная параметризация разрешает возникшую в метаболическом подходе проблему разносортности элементов в универсумах.
Энтропийная параметризация появилась в результате математического приема замены упорядочения структур систем упорядочением чисел. Поэтому можно сказать, что энтропийная параметризация изменчивости вторична по отношению к способу упорядочения систем при помощи гомоморфизмов. В рассмотренном выше формализме проводилось сравнение систем с помощью мономорфизмов (по аналогии с инъекциями для сравнения неструктурированных множеств). Вообще говоря, для сравнения структур вместо мономорфизмов в категории могут быть выбраны иные морфизмы. Кроме основного одноместного функтора, породившего энтропию, могут оказаться монотонными по отношению к упорядочению структур и другие функторы, а может оказаться, что таких функторов не существует вовсе. Таким образом, параметризация времени с помощью структурных чисел (назовем ее категорным временем) является более общей конструкцией, чем энтропийный способ. Правда, как уже отмечалось, структурные числа упорядочены лишь частично и вводимое ими время обладает тем самым довольно экзотическими свойствами.
Энтропийное (и вместе с ним метаболическое) время согласовано с упорядочением структур при помощи инъективных морфизмов (т.е. вложений). Поэтому согласно экстремальному принципу эволюция сиcтем идет от подобъектов к объектам и от них — к надобъектам. Такую эволюцию можно назвать консервативной или казуальной: достигнутые состояния не пропадают (подобъект “сохраняется” в объекте) и новые состояния возникают не на пустом месте, а из своих “менее сильных” (в смысле упорядочения по “силе структур”) предшественников.
Отказ от использования мономорфизмов в качестве упорядочивающих морфизмов при описании некоторой системы может привести к изменению и только что сформулированного принципа консервативной эволюции естественных систем. По-видимому, выбор упорядочивающих морфизмов — вопрос экспликации операциональных способов выяснения принадлежности элементов объектам. Естественнонаучной интерпретацией конструкции упорядочивающих морфизмов может, по-видимому, служить понятие сигнала.
Теорема теории категорий, устанавливающая монотонность упорядочения структур и их энтропийных инвариантов (Левич, 1982, с.113) фактически играет роль H-теоремы Больцмана, доказывающей монотонность энтропии, но не в физическом, а в категорном времени. Аналогична роль предъявленной выше монотонной связи энтропийного и метаболического времен.
Поскольку в процессе изменчивости системы интервал ее метаболического времени Dt = Dm+ + Dm- строго возрастает, то вдоль траектории системы в пространстве состояний возрастает и энтропия системы. Это означает, что с помощью энтропии можно параметризовать изменчивость или задавать количественную меру изменения состояний системы. Таким образом возникает T-компонент теоретико-категорного описания систем, или энтропийное время систем.
Как указывалось, для разработки динамической теории какого-либо фрагмента реальности необходимо решение конкретного ряда методологических проблем: построение элементарного объекта теории, перечисление допустимых состояний объектов и путей их изменчивости, конструирование способов параметризации изменчивости и, наконец, формулировка закона изменчивости, выделяющего реальное обобщенное движение объектов в пространстве состояний из всех возможных.
Результаты настоящей главы позволяют предложить:
- в качестве элементарного объекта — иерархию структурированных множеств, не замкнутых относительно замены элементов на каких-либо уровнях иерархии;
- в качестве пространства состояний — категорию, объекты которой (элементарные объекты теории) интерпретируются как состояния изучаемой системы, а морфизмы — как способы изменчивости системы;
- в качестве часов — параметризацию изменчивости, которая задается энтропией состояний системы, рассчитываемой через значения основного одноместного функтора категорий. Энтропийная параметризация комонотонна с метаболической, задаваемой количеством замененных в системе элементов;
- в качестве закона изменчивости — принцип максимума энтропии при условиях, накладываемых ограниченностью доступных системе ресурсов.
Предложенный подход к описанию естественных систем, конечно, недостаточен для построения теории и представляет собой лишь некоторые основания для потенциальной исследовательской программы. Эта программа должна, в частности, включать возможность последовательного получения традиционных уравнений динамики в предметных областях, где такие уравнения уже известны, т.е. обеспечивать выполнение принципа соответствия. Получение уравнений мыслится как следствие принципа экстремальности энтропии в отличие от исследовательской программы И.Пригожина (1985), в которой динамические уравнения считаются исходно заданными и речь идет о дополнении их способами введения энтропии (как функции Ляпунова динамических уравнений) и принципами отбора допустимых состояний на основе второго начала термодинамики.
§ 3. Гипотеза генерирующих потоков
Можно ли, научившись параметризировать время субституционными или энтропийными часами, сказать что-либо о происхождении самой изменчивости, т.е. о природе течения времени или о происхождении генерального процесса?
В рамках слабой гипотезы (см. п.1.3), т.е. работая с надмолекулярными уровнями, например, биологической иерархии (молекулы, клетки, организмы, популяции, сообщества, биосфера), на вопрос о происхождении изменчивости ответить можно: потоки субстратов и энергии в биосфере Земли порождаются исходным потоком фотонов Солнца, который обуславливает и генерирует все иные потоки в биологической иерархии.
Такую точку зрения обобщает сильная гипотеза. Не только любое движение имеет метаболическую природу (движение объекта в среде есть поглощение и испускание объектом элементов среды; пространство есть среда, составленная из предэлементов), но и происхождение замен элементов обязано внешнему потоку, пронизывающему содержащую объекты естественную иерархию. Иными словами, если уместна аналогия между биосферой и вселенной как системами (под вселенной я понимаю лишь доступную инструментальным методам измерения область), то и время вселенной порождается некоторым генерирующим потоком предэлементов одного из довольно глубоких уровней физической иерархии, т.е. вселенная не изолирована, не замкнута, не равновесна. Именно неравновесность вселенной порождает в ней течение времени.
Подобное утверждение почти очевидно для биологических иерархий, интерпретируемо для геологических и географических универсумов, но кажется совершенно неприемлемым для физических объектов. Легко предъявить примеры равновесных систем, для которых течение физического времени очевидно: свободное движение тела, колебания маятника, движение взаимодействующих тел в замкнутой и изолированной системе (например, планет вокруг Солнца). Но и здесь есть поток, для обнаружения которого достаточно лишь изменить язык описания механического движения. Представим себе перемещение тела как поглощение им одних точек геометрического пространства и испускание других. Формально такое описание может быть сделано совершенно аналогичным описанию движения по геометрическим траекториям.
Ассоциации, связанные с идеей порождающего потока, не новы ни в философии, ни в естествознании. Это и картина мира в даосизме, и современный физический вакуум, и квазисубстанциональная концепция Дж.Уитроу, касающаяся “гипотезы..., согласно которой имеется единый основной ритм вселенной” (1964, с.63). Это и поток абсолютного времени И.Ньютона (правда, ньютоновский поток полностью независим от материи (Newton, 1687), а генерирующий поток непосредственно связан с материальными объектами). Это и поток времени Н.А.Козырева (1982), который формирует причинность в мире, является одним из источников энергии звезд, обуславливает новое “метавзаимодействие” (Еганова, 1984) объектов мира. В работе И.А.Егановой приведены многочисленные указания на эксперименты, объяснение которых, по-видимому, требует привлечения идей Н.А.Козырева (см. также серию экспериментальных работ последних лет М.М.Лаврентьева с соавторами, 1990, 1991, 1992). Обзору и развитию идей Н.А.Козырева посвящен второй том настоящей книги. Это и поток “рождающейся из пространства-времени материи” (Grunzig et. al., 1987; Prigogine et. al., 1989; Пригожин, Стенгерс, 1994, с.232) в неравновесном варианте общей теории относительности.
Отождествление течения времени и существования субстанционального потока часто встречается с тем возражением, что понятие потока вроде бы уже включает в себя предварительное представление о времени: обычно потоком называют изменение в физическом времени концентрации вещества или поля. Однако возможно и более общее понимание потока. Это понимание зафиксировано субституционной конструкцией времени: вхождение элементов в некоторую эталонную систему рассматривается как поток элементов в системе, акты вхождений называются моментами времени, количество вхождений задает меру времени-потока. Другими словами, изменение количества элементов в эталонной системе параметризуется не каким-либо внешним процессом (не “физическим временем”), а процессом замены элементов в той же системе. Для генерирующего потока эталонной системой является вселенная, открытая по отношению к вхождению предэлементов некоторого глубинного уровня строения материи. Изменение количества указанных предэлементов, т.е. поток предэлементов, задает время вселенной.
Появившись как логическая экстраполяция свойств метаболического времени, генерирующий поток позволяет конструктивно искать подходы к существующим проблемам естествознания. Связь между течением времени и неравновесностью, диссипацией потоков и необратимостью тривиальна: неравновесность системы, т.е. наличие субстанционального потока через нее и есть течение времени. Нетривиально то, что для этой тривиальности обязательно должен онтологически существовать генерирующий поток. Вопросы о “природе” времени, причинах его “течения”, механизмах становления переводятся гипотезой генерирующего потока в вопрос о происхождении и статусе субстратной и энергетической “подпитки” нашей вселенной.
В конструкции времени генерирующий поток представляет фундаментальный, первичный эталонный объект для принципа упорядочения (см. п.1.4), другими словами, порождает последовательность моментов времени. Время оказывается линейно упорядоченным потому, что таков генерирующий поток. Необратимость времени — не имманентное его свойство, а привносится во вселенную вместе с направленностью потока предчастиц: необратимость времени существует, пока не обращен генерирующий поток. Замечу, что отсутствие обратимости может быть следствием специальных запретов, например, перехода тепла в работу (второе начало термодинамики) или “преобразования материи в пространство-время” (Пригожин и Стенгерс, 1994, с.232). Более общим образом в рамках субституционного подхода можно утверждать, что необратимость может быть связана с иерархичностью естественных систем и с несимметричностью отношения принадлежности предэлементов элементам.
Таким образом, генерирующие потоки порождают становление в мире: различие между прошлым и будущим систем состоит в различном количестве элементов субстанции соответствующего иерархического уровня в этой системе. По отношению ко времени модель в определенной степени снимает оппозицию между реляционными и субстанциональными подходами. Дело в том, что традиционные реляционные модели времени (см., например, главу В.В.Аристова в настоящей книге) постулируют частицы материи и их движение, время же становится конструктом теории. Описываемый здесь подход возлагает ответственность за феномен на субстанцию одного из уровней иерархического строения систем (если угодно — та же материя, но в специфической форме), движение постулируется принципом изменчивости, а субституционные часы и феномен становления становятся конструктами теории, т.е. реляционный и субстанциональный подходы оказываются схожими по своей структуре, только первый из них имеет дело с материальными объектами в известной форме, а второй — с материей, не идентифицируемой пока современными научными технологиями.
Гипотеза генерирующего потока в значительной степени радикальна и способна повлиять на многие области естествознания. Сдержанно настроенному читателю можно предложить рассматривать гипотезу потока лишь как удобное средство описания феноменов становления, течения времени, развития, т.е., если угодно, перевести представления о потоке из области онтологии в методы гносеологии. Впрочем, конструктивная постановка вопроса, по-видимому, состоит не в умозрительных спорах о том, существует ли порождающий поток, а в том, существуют ли способы его операционально предъявить, т.е. воспроизводимо измерить какие-либо характеристики потока, отличные от основного его проявления — течения времени.
Переформулировка свойств и проблем времени на языке свойств генерирующего потока (свойств, постулируемых так же, как исходные свойства времени) может тем не менее оказаться полезной, по крайней мере, в двух отношениях: во-первых, — открывая новые эвристики, во-вторых, — уменьшая набор исходных сущностей и упрощая тем самым логическое обоснование научной картины мира. Гипотеза генерирующего потока достаточна, чтобы конструировать и время, и пространство, и частицы, и взаимодействие... Предъявлю несколько подобных эвристик, напомнив, что излагаются не строгие результаты, а только лишь исследовательская программа разработки метаболического подхода.
Источники вхождения во вселенную (или стоки из нее) генерирующего потока отождествим с заряженными частицами мира. Допускается существование нескольких генерирующих потоков во вселенной, т.е. вселенная не замкнута по отношению к потокам предэлементов нескольких глубинных уровней ее строения. Заряды частиц есть динамические характеристики потоков, источниками которых являются частицы. Различные виды зарядов порождаются генерирующими потоками различных уровней иерархии.
Суперпозиция элементов глубинных уровней естественных иерархий образует пространство (синонимы — среда для частиц, субстанциональный “эфир”, физический вакуум). Метаболическое движение объектов в пространстве (эфире) происходит не путем “раздвигания” элементов эфира, а путем проникновения этих элементов в объекты и замены уже имеющихся в объекте элементов, т.е. “эфирного трения”, “эфирного ветра” не существует. Наглядными образами строения объектов из эфира будут не вихри или торы, а “фонтаны” или бьющие в водоем “ключи”. Последовательности “излученных” частицами предэлементов образуют систему окрестностей частицы и порождают понятие “близости” в пространстве и конструкцию топологии пространства.
Предположение о том, что материальные частицы есть “входы” или “выходы” генерирующих потоков в нашей вселенной, позволяет предложить лесажевский (Розенберг, 1935) механизм взаимодействия частиц: “Современное доказательство теоремы Ньютона основано на гидродинамических соображениях, восходящих к Лапласу: дело в том, что единственное сферически симметричное течение несжимаемой жидкости — это течение по радиусам со скоростью, обратно пропорциональной квадрату расстояния от центра... Итак, силовое поле притяжения точечной массой математически совпадает с полем скоростей течения несжимаемой жидкости” (Арнольд, 1987). Истечение и поглощение предэлементов можно рассматривать как обмен предэлементами между частицами, что соответствует традиционной для теоретической физики конструкции взаимодействия. Различным генерирующим потокам соответствуют как различные виды зарядов, так и различные виды взаимодействия. Согласно теореме стратификации (см. п.2.4) в каждой области пространства системы ее движение определяется некоторыми из генерирующих потоков и не определяется другими, т.е. разные типы взаимодействия проявляются в различных областях пространства системы (Левич, 1995).
В зависимости от выбора в качестве эталона измерения времени того или иного генерирующего потока (различные генерирующие потоки могут оказаться неравномерными друг относительно друга) возможна элиминация этого взаимодействия из описания движения. Например, для идеального физического времени законов механики роль постулата императивности играет аксиома инерции, согласно которой равны отрезки времени, за которое тело проходит равные пути при отсутствии взаимодействия с другими телами, т.е. равномерность временно¢ й шкалы однозначно связана с отсутствием или наличием взаимодействия объектов. Любое нелинейное преобразование переменной времени в уравнениях механики приводит к появлению членов, ответственных за дополнительное взаимодействие (Мизнер и др., 1977). Таким образом, взаимодействие может быть описано с помощью нелинейных шкал времени.
В общей теории относительности сходная идеология доведена до логического завершения: вместо картины мира, в которой существует взаимодействие в плоском пространстве-времени, предлагается обладающий кривизной мир (уже не только время), где необходимость в представлениях о взаимодействиях (гравитационных) отсутствует. Э.Милн (Milne, 1948) добился аналогичного результата элиминации взаимодействия за счет преобразования координат, оперируя лишь нелинейной модификацией шкалы времени.
Неравномерность временно¢ й шкалы можно трактовать как неоднородность времени, из которой по теореме Нетер следует несохранение энергии. Для метаболической конструкции такое несохранение некриминально, поскольку течение метаболического времени возникает только в системах, открытых внешнему потоку предчастиц, и вопрос об однородности, равномерности этого потока — вопрос выбора эталонного уровня определения времени. Если эталон будет выбран так, чтобы поток был равномерен, то в соответствующих уравнениях движения взаимодействие будет отсутствовать и энергия сохраняться. Если выбор повлечет неравномерность потока, то в уравнениях появятся силы и несохранение энергии станет узаконенным.
Субституционный подход позволяет попытаться ввести конструкцию причинности. Рассмотрим ситуацию, в которой предэлемент генерирующего потока испускается частицей-источником и поглощается некоторым другим объектом. Назовем описанный процесс причинным звеном, акт испускания фиксированного предэлемента — причиной в причинном звене, а акт поглощения того же предэлемента — следствием. При конечной “скорости распространения генерирующего потока” (согласно интерпретациям п.1.3 это соответствует ненулевому среднему чиcлу ![]() предэлементов в элементах) причина и следствие оказываются разделены пространственно-временны¢
м интервалом. Более подробное обсуждение аспектов взаимосвязи между “потоком времени” и представлениями о причинности содержится во втором томе настоящей книги, посвященном идеям Н.А.Козырева.
предэлементов в элементах) причина и следствие оказываются разделены пространственно-временны¢
м интервалом. Более подробное обсуждение аспектов взаимосвязи между “потоком времени” и представлениями о причинности содержится во втором томе настоящей книги, посвященном идеям Н.А.Козырева.
Распространение генерирующего потока по отношению к частицам-источникам оказывается двух “знаков” — испускание или поглощение. Выделенное направление потока, кроме течения времени, порождает неравноправность правых и левых систем координат, а также различные знаки зарядов. Мысленная операция “обращения” потока должна приводить к трем согласованным эффектам: к обращению направления времени (несохранение “временно¢ й четности”), к замене правых систем координат на левые или наоборот (несохранение “пространственной четности”) и к замене знака зарядов частиц (изменение “зарядовой четности”; античастица, как принято в квантовой электродинамике, оказывается частицей, движущейся “против времени”). Обращение генерирующего потока (и существующее согласованное изменение зарядовой, пространственной и временно¢ й четностей), по-видимому, не меняет состояние мира.
Если физические процессы разыгрываются в среде из предэлементов, которые сами не являются частицами и истечение которых порождает обладающие массой и другими зарядами частицы, то надмолекулярные иерархии, связанные, в частности, с жизнью, задаются уже средами из самих частиц.
Генеральный процесс, лежащий в основе метаболической конструкции времени, обладает рядом свойств, которые подчеркивают его сходство с процессом, называемым жизнью и рассматриваемым как совокупность сопряженных изменений: обмена веществ, роста, развития, размножения, эволюционных преобразований... Генеральный процесс — понятие, заведомо менее целенаправленное на представления о жизни, чем например, “устойчивое неравновесие” Э.Бауэра (1935), хотя бы уже потому, что включает также процессы деградации и распада. Тем не менее попытки осмысливания свойств биологического времени могут оказаться почти тем же самым, что и описание сущности жизни. К такому заключению приходит В.П.Войтенко (1985, с.74): “Сопряженность “технологии” измерения времени с такими фундаментальными процессами, как рост и деление клетки или обмен веществ, указывает на то, что биологические часы — не пристройка к зданию биосистемы, а само здание”. На сходство жизни и генерального процесса обращает внимание П.Б.Гофман-Кадошников (1984), подчеркивая, что самообновление путем смены элементов — основное системное свойство жизни, отличающее биологические системы от физических и химических. По мнению Г.Е.Михайловского (1989, см. также главу настоящей книги), именно временна¢ я организация биологических систем определяет качественную специфику живого. Тождественность двух так интересующих нас процессов хотел подчеркнуть и В.И.Вернадский (1967, с.65), приводя принадлежащие классику слова: “Жизнь представляет более или менее быстрый, более или менее сложный вихрь, направление которого постоянно и который всегда захватывает молекулы, обладающие определенными свойствами; но в него постоянно проникают и из него постоянно выбывают индивидуальные молекулы, так что форма живого тела для него существеннее, чем вещество. Пока это движение существует, тело, в котором оно имеет место, живо... Когда движение окончательно останавливается, тело умирает” (Cuvier, 1817).
Гипотеза генерирующих потоков допускает и более радикальные, чем аналогии с метаболическим движением, предположения о специфике явлений жизни. Так же как частицы-заряды являются источниками генерирующих потоков, порождающих физические взаимодействия, так и живые организмы есть источники специфических потоков предэлементов каких-то иерархических уровней строения материи (Levich, 1993; Левич, 1993). Различные потоки могут быть ответственны за свойства жизни, сознания, пассионарности (о пассионарности см. Л.Н.Гумилев, 1989). Свойства жизни по своему происхождению становятся аналогичными свойствам, например, электрического или барионного заряда. Отличие живого от неживого оказывается связанным со специфичностью и количеством задействованных в феномене времени генерирующих потоков.
Искушенный читатель может увидеть в гипотетических субстанциональных потоках метаболического подхода возрождение жизненных сил витализма, например, энтелехии Аристотеля, vis essentialis Вольфа или nesus Блуменбаха (Дриш, 1915). Однако утверждения метаболической концепции значительно прозаичнее: речь идет о вполне материальных, но не регистрируемых средствами современных научных технологий уровнях строения естественных систем. Гипотетические потоки предэлементов этих уровней нужны не специально для введения жизненных сил, а отвечают в метаболическом подходе логике вывода целого круга конструкций, связанных с феноменом времени в естествознании.
3.3. Избавление от жупела “тепловой смерти”
Признание генерирующих потоков снимает оппозицию второго начала термодинамики существованию феноменов развития, поскольку второе начало относится исключительно к изолированным системам. Отпадает приложимость второго начала к той открытой части вселенной, где генерирующие потоки порождают течение времени, что, по-видимому, не составляет открытия ни для физиков, ни для астрономов: “...ежедневный опыт убеждает нас в том, что свойства природы не имеют ничего общего со свойствами равновесной системы, а астрономические данные показывают, что то же самое относится и ко всей доступной нашему наблюдению колоссальной области вселенной” (Ландау, Лифшиц, 1964, с. 45-46), более того, “отдельные небесные тела и их системы так изолированы друг от друга, что для них тепловая смерть должна заметно приблизиться прежде, чем произойдет вмешательство сторонней системы. Поэтому деградированные состояния систем должны бы преобладать, а вместе с тем они почти не встречаются. И задача состоит не только в том, чтобы объяснить неравновесность Вселенной в целом, она имеет значительно более конкретный смысл — понять, почему отдельные системы и сами небесные тела продолжают жить, несмотря на короткие сроки релаксации” (Козырев, 1963, с.96).
Основанная на принципе экстремальной энтропии теория (см. §2) не возвращает исследователей ко второму началу термодинамики, поскольку прилагается к открытой для субстратов и энергии системе. К тому же формула обобщенной энтропии получена вне каких-либо вероятностных предпосылок, из-за чего исчезает интерпретация экстремального принципа как требования перехода от менее вероятного к более вероятному состоянию. Ограничения развития системы доступными потоками субстратно-энергетических ресурсов при решении вариационной задачи (2.4) приводят не к однородному, а к крайне неравномерному распределению характеристик системы типа распределения Гиббса (формула (2.5) в п.2.4), а также влекут возможности порождения структур, т.е. самоорганизацию.
Для вариационной задачи (2.4) (в более общей — не чисто экологической интерпретации) справедлив аналог теоремы Гиббса, согласно которому задача на максимум энтропии с ограничениями сверху генерирующими потоками эквивалентна задаче на минимум любого из генерирующих потоков с ограничениями снизу на структурный инвариант системы, т.е. экстремальный принцип приобретает смысл минимального “потребления” генерирующей субстанции или минимального субституционного времени. Еще одна интерпретация экстремального принципа — увеличение сложности в процессе естественной эволюции открытых, неизолированных систем или увеличение степени их самоорганизации.
Энтропийный экстремальный принцип во вселенной, открытой для генерирующих потоков, совершенно меняет взгляд на эволюцию мира. Вот каким рисует будущее вселенной И.Д.Новиков (1990, с.181-189): “...Если во Вселенной нет заметных количеств материи между галактиками, которая почему-либо не видна, то она всегда будет расширяться... Примерно через сто тысяч миллиардов лет погаснут самые последние звезды... Несмотря на отсутствие пока прямых экспериментальных данных, вся совокупность наших физических знаний указывает на то, что вещество вселенной не стабильно и хотя очень медленно, но распадается... происходит и процесс квантового испарения черных дыр, которые остаются после смерти некоторых массивных звезд и существуют в ядрах галактик. Таким образом и остывшие звезды, и разреженный газ, а затем и черные дыры в далеком будущем исчезнут из Вселенной... во Вселенной останутся только редкие электроны и позитроны, разбросанные в пространстве на гигантские расстояния друг от друга”.
Еще более радикально будущее мира согласно “принципу Гельвеция” (“Время, зуб которого разжевывает железо и пирамиды, видит лишь смерть, которую оно приносит” (Гельвеций, 1974, с.114)) описывает Ю.Б.Молчанов (1990, с.133): “...во времени исчезает все, и исчезает без следа, и в этом-то и состоит подлинная сущность времени”.
Гипотеза генерирующих потоков позволяет противопоставить принципу Гельвеция (или, если угодно, принципу Хроноса — бога, пожиравшего своих детей) принцип, который стоило бы назвать “принципом Козырева” (“Очевидно, в самых основных свойствах материи, пространства, времени должны заключаться возможности борьбы с тепловой смертью противоположными процессами, которые могут быть названы процессами жизни. Благодаря этим процессам поддерживается вечная жизнь Вселенной.” (Козырев, 1963, с.96)): пока вселенная открыта для генерирующих потоков, ее эволюция сопровождается самоорганизацией, ростом неоднородности и сложности.
Литература
Aбакумoв В.А. Длина и частoта пoкoлений // Труды ВНИРО. 1969. Т.67. С.344-356.
Алексеев В.П. Вектoр времени в таксoнoмическoм кoнтинууме // Вoпрoсы антрoпoлoгии. 1975. Вып.49. С.65-77.
Аристoтель. Сoчинения в 4 т. Т.3: Физика. М., 1981.
Арнoльд В.И. Трехсoтлетие математическoгo естествoзнания и небеснoй механики // Прирoда. 1987. №8. С.5-15.
Бауэр Э.С. Теoретическая биoлoгия. М., 1935.
Бурбаки Н. Архитектура математики // Очерки пo истoрии математики. М., 1963. С.245-259.
Васильев В.К., ЛукьЯнoв Н.К., Саввин А. Кoнцепция сoбственнoгo времени биoлoгических прoцессoв и ее применение для изучения динамики газooбмена // Кoсмическая биoлoгия и авиакoсмическая медицина. 1974. №5. С.12-17.
Вернадский В.И. Очерки геoхимии // Биoсфера. М., 1967.
Вернадский В.И. Проблемы биохимии // Труды биогеохимической лаборатории. XVI. М., 1980.
Вернадский В.И. Филoсoфские мысли натуралиста. М., 1988.
Винoградoв М.Е., Шушкина Э.А. Сукцессия мoрских планктoнных сooбществ // Океанoлoгия. 1983. Т.23., вып.4. С.633-639.
Вoйтенкo В.п. Время и часы как прoблема теoретическoй биoлoгии // Вoпрoсы филoсoфии. 1985. №1. С.73-82.
Гаврилoв Г.П., СтoлЯрoв А.Ю., ЛевиЧ А.П. Адекватнoсть альтернативных мoделей в экoлoгии сooбществ // Экoлoгический прoгнoз. М., 1986. С.188-196.
Гельвеций К.Ф. Записные книжки // Сoчинения. Т.1. 1974.
Гoфман-Кадoшникoв П.Б. Системный анализ иерархии урoвней жизни // Системные исследoвания. М., 1984. С.322-328.
Гудвин Б. Временна¢ я oрганизация клетки. Динамическая теoрия внутриклетoчных регулятoрных прoцессoв. М., 1966.
Гумилев Л.Н. Этнoгенез и биoсфера Земли. Л., 1989.
Детлаф Т.А., Детлаф А.А. Безразмерные критерии как метoд кoличественнoй характеристики развития живoтных // Математическая биoлoгия развития. М., 1982. С.25-39.
Дмитриев В.Ю. Некoтoрые вoпрoсы изучения изменений систематическогo разнooбразия искoпаемых oрганизмoв // Палеoнтoлoгический журнал. 1978. №2. С.122-132.
Дриш Г. Витализм. М., 1915.
Еганoва И.А. Аналитический oбзoр идей и экспериментoв сoвременнoй хрoнoгеoметрии. 1984. Деп. ВИНИТИ. №6423-84.
Зoтин А.И., Алексеева Т.А. Кoнстанта Рубнера как критерий видoвoй прoдoлжительнoсти жизни // Физиoл. журн. 1984. Т.30., №1. С.59-64.
Кoзырев Н.А. Причинная механика и вoзмoжнoсть экспериментальнoгo исследoвания свoйств времени // Истoрия и метoдoлoгия естественных наук. Вып.2. М., 1963. С.95-113.
Кoзырев Н.А. Время как физическoе явление // Моделирoвание и прoгнoзирoвание в биoэкoлoгии. Рига, 1982. С.59-72.
Лаврентьев М.М., Еганoва И.А., Луцет М.К., Фoминых С.Ф. О дистанциoннoм вoздействии звезд на резистoр // Дoкл. АН СССР. 1990. Т.314, №2. С.352-355.
Лаврентьев М.М., Гусев В.А., Еганoва И.А., Луцет М.К., Фoминых С.Ф. О регистрации истиннoгo пoлoжения Сoлнца // Дoкл. АН СССР. 1990. Т.315, №2. С.368-370.
Лаврентьев М.М., Еганoва И.А., Луцет М.К., Фoминых С.Ф. О регистрации реакции вещества на внешний неoбратимый прoцесс // Дoкл. АН СССР. 1991. Т.317, №3. С.635-639.
Лаврентьев М.М., Еганoва И.А., Медведев В.Г., Олейник В.К., Фoминых С.Ф. О сканирoвании звезднoгo неба датчикoм Кoзырева // Дoкл. АН. 1992. Т.323, №4. С.649-652.
Ландау Л.Д., Лифшиц Е.М. Статистическая физика. М., 1964.
ЛевиЧ А.П. Инфoрмация как структура систем // Семиoтика и инфoрматика. 1978. №10. С.116-132.
ЛевиЧ А.П. Структура экoлoгических сooбществ. М., 1980.
ЛевиЧ А.П. Теoрия мнoжеств, язык теoрии категoрий и их применение в теoретическoй биoлoгии. М., 1982.
ЛевиЧ А.П. Тезисы о времени естественных систем // Экологический прогноз. М., 1986, С.163-190.
ЛевиЧ А.П. Метаболическое время естественных систем // Системные исследования. Ежегодник. 1988. М., 1989. С.304-325.
ЛевиЧ А.П. Время как изменчивость естественных систем и как способ ее параметризации. Деп. ВИНИТИ. М., 1989. №7599-89.
ЛевиЧ А.П. Теoретическая биoлoгия: пoиск уравнений oбoбщеннoгo движения и истoчникoв неравнoвеснoсти живой материи // Изв. РАН. Сер. биoл. 1993. №5. С.778-779.
ЛевиЧ А.П., Алексеев В.Л., Никулин В.А. Математические аспекты вариациoннoгo мoделирoвания в экoлoгии сooбществ // Математическoе мoделирoвание. 1994. Т.6, №5. С.55-71.
ЛевиЧ А.П., Алексеев В.Л., Рыбакoва С.Ю. Оптимизация структуры экoлoгических сooбществ: мoдельный анализ // Биoфизика. 1993б. Т.38, вып.5. С.877-885.
ЛевиЧ А.П., ЗамoлoдЧикoв Д.Г., Рыбакoва С.Ю. Исследoвание адекватнoсти теoретикo-категoрнoй мoдели фитoпланктoнных сooбществ // Прoблемы экoлoгическoгo мoнитoринга и мoделирoвания в экoлoгии. Т.15. Л., 1993а. С.234-246.
ЛевиЧ А.П., Любимoва Е.Д., Марташвили Г.Ш. Видoвая структура и пoтребление субстратнo-энергетических фактoрoв в лабoратoрных альгoценoзах // Экoлoгический прoгнoз. М., 1986б. С.69-103.
ЛевиЧ А.П., Ревкoва Н.В., Булгакoв Н.Г. Прoцесс “пoтребление-рoст” в культурах микрoвoдoрoслей и пoтребнoсти клетoк в кoмпoнентах минеральнoгo питания // Экoлoгический прoгнoз. М., 1986а. С.132-139.
Мартынoв Д.Я. Века и мгнoвения. М., 1961.
Мизнер Ч., Тoрн К., Уилер Дж. Гравитация. М., 1977.
Михайлoв И.И. Физикo-геoграфическoе райoнирoвание. М., 1985.
Михайлoвский Г.Е. Пoнятие энтрoпии в прилoжении к самoвoспрoизвoдящимся биoлoгическим системам // Челoвек и биoсфера. Вып.6. М., 1982. С.62-78.
Михайлoвский Г.Е. Описание и oценка сoстoяний планктoнных сooбществ. М., 1988.
Михайлoвский Г.Е. Организация времени в биoлoгических системах // Журнал oбщей биoлoгии. 1989. Т.50, №1. С.72-81.
Мoисеева Н.И. Свoйства биoлoгическoгo времени // Фактoр времени в функциoнальнoй oрганизации деятельнoсти живых систем. Л., 1980. С.15-20.
МoлЧанoв Ю.В. Прoблема времени в сoвременнoй науке. М., 1990.
На пути к теoретиЧескoй биoлoгии. Под ред. С.Уодингтона. Т.1. Прoлегoмены. М., 1970.
Нoвикoв И.Д. Куда течет река времени? М., 1990.
Пригoжин И. От существующегo к вoзникающему. М., 1985.
Пригoжин И., Стенгерс И. Время, хаос, квант. М., 1994.
Рoзенберг Ф. Истoрия физики. Ч.3. Вып.1. М.-Л., 1935.
Свирежев Ю.М., Пасекoв В.П. Оснoвы математическoй генетики. М., 1982.
Уитрoу Дж. Естественная филoсoфия времени. М., 1964.
Уранoв А.А. Вoзрастнoй спектр фитoценoпoпуляции как функция времени и энергетических вoлнoвых прoцессoв // Научн. дoкл. высшей шкoлы. Биoлoгические науки. 1975. №2. С.7-34.
Флейшман Б.С. Темпoральнo-биoлoгический “закoн лoгарифма” как следствие oбщесистемнoгo гипербoлическoгo закoна надежнoсти регенерирующих систем // Темпoральные аспекты мoделирoвания и прoгнoзирoвания в экoлoгии. Рига, 1986. С.85-97.
Френкель А., Бар-Хиллел И. Оснoвания теoрии мнoжеств. М., 1966.
Фридман А.А. Мир как прoстранствo и время. М., 1965.
Чебураева А.Н. Периодичная динамика ценoпoпуляций oвсеца Шелля в северных лугoвых степях // Ценoпoпуляции растений: развитие и взаимoотнoшения. М., 1977. С.50-57.
Шарoв А.А. Пoнятия инфoрмации в теoрии категoрий // Семиoтика и инфoрматика. Вып.8. М., 1977. С.167-178.
Шмидт-Ниельсoн К. Размеры живoтных: пoчему oни так важны? М., 1987.
Backman G. Wachstum und Organische Zeit. Leipzig, 1943.
Cuvier G. Le regne animal distribue d'apres son organisation. Paris, 1817. P.12-13.
Gunzig e., gehenian j., prigogine i. entropy and cosmology // Nature. 1987. V.330. P.621-624.
Hofecker G., Skalicky M., Kment A., Niedermuller M. Mathematical models of the biological age of the rat // Adv.Physiol.Sci. 1981. V.34. P.47-52.
Levich A.P. Toward a dynamic theory. Lectures in Theoretical Biology. V.2. Tallinn, 1993.
Levich A.P. Generating flows and a substitutional model of space-time // Gravitation & Cosmology. 1995. V.1, №3. P.237-242.
Lurie D., Valls J., Wagensberg J. Thermodynamic approach to biomass distribution in ecological systems // Bull. of Mathematical Biology. 1983. V.45, №5. P.869-872.
McCay C.M., Crowell M.F., Maynard L.A. The effect of retarded growth upon ultimate body size // J.Nurt. 1935. V.10. P.62-79.
Milne E.A. Kinematic Relativity. Oxford, 1948.
Newton J.S. Philosophiae Naturalis Principia Mathematica. London, 1687.
Noüy L.P. Biological Time. London, 1936.
prigogine i., gehenian j., Grunzig e., Nardone p. Thermodynamics and cosmology // General Relativity and Gravitation. 1989. V.21. P.1.
Robinson A. Non-Standart Analysis. Amsterdam, 1966.
Shaher B.L. Ageing of Nesokia by weighing the eye lens //Pacistan. J. Zool. 1982. V.14 (1). P.103-105.
Thornwaite C.W. Operations research in agriculture // J. of the operations research society of America. 1953. №1. P.33-38.
Tomson W., Tait P.G. Natural Philosophy. Cambridge, 1890.
Whitehead A., Russel B. Principia Mathematica. V.3. Cambridge, 1910-1913.