 . Тел.: 939--5560.
. Тел.: 939--5560.Время в бытии естественных систем
А.П.Левич
Московский государственный университетим. М.В.Ломоноcова 119899, Москва, Воробьевы горы, МГУ, Биофак,кафедра зоологии позвоночных и общей экологии. E-mail:
 . Тел.: 939--5560.
. Тел.: 939--5560.
Аннотация
Ряд противоречий в современной научной картине Мира подталкивает к разработке
явной конструкции времени и вместе с тем к переосмысливанию многих базовых
понятий науки.
Предложена модель часов, параметризующая изменения естественных систем
количеством замен (субституций) элементов в них. Предложена гипотеза
происхождения замен, благодаря субстанциональным генерирующим потокам, по
отношению к которым открыты все естественные системы.
Предложенные подходы позволяют описывать феномен становления и формулировать
экстремальные принципы движения систем. Изучены свойства субституционного
времени, субституционного движения, симметрий Мира. Намечены пути к
конструированию пространства и уравнений движения систем.
Мотивы изучения времени
Время – одна из немногих неуловимых и неподвластных человеческой воле
сущностей мира, которая волнует чувства и умы современников не меньше, чем их
далеких предков. В неослабевающем интересе к феномену времени заключены не
только его экзистенциональная человеческая сущность – вечное неприятие
бренности и краткости личного бытия, но и бескорыстное любопытство к
естественнонаучной природе времени – происхождению нового и источникам
изменений в мире.
В нынешнем естествознании время – исходное и неопределяемое понятие. Тем не
менее, интуитивные представления исследователей о времени значимо влияют на
опытные и теоретические результаты научной работы. Исповедуемая концепция
времени важна во многих областях познания и деятельности, например, при
измерении возраста систем или при введении их собственного времени, в научном
прогнозировании, при экспериментальном изучении времени, при поиске
фундаментальных законов динамики и развития систем и при поиске причин,
порождающих динамику или эволюцию.
Динамическая теория какого-либо фрагмента реальности включает (чаще всего
неявно) несколько обязательных компонентов: описание элементарного объекта
теории; набор допустимых состояний объектов теории; способы параметризации,
т.е. количественного описания этой изменчивости (часы); основной компонент
– формулировка закона изменчивости (например, уравнения движения объектов)
и, наконец, интерпретирующие процедуры сопоставления формальным конструктам
теории понятий предметной реальности и экспериментально измеряемых величин
(Левич, 1993, Levich, 1995a).
В существующих динамических подходах наименее разработаны компоненты,
вводящие изменчивость объектов мира ("предвремя" системы) и способы ее
измерения (параметрическое время – часы). В качестве часов, как правило,
используются физические процессы. Однако исследователей систем нефизического
происхождения все чаще не удовлетворяют физические эталоны изменчивости, и в
понятийном аппарате возникают представления о специфических временах –
биологическом, геологическом, психологическом, социальном и т.д. (Study of
Time, 1981).
Поэтому основная задача в изучении динамического аспекта существования
систем – создание явной конструкции времени, пригодной для интуиции
исследователей различных областей реальности.
Предлагаемая конструкция по-возможности должна позволить:
-ввести в научный обиход понятийные и эмпирические референты для
феномена становления, или "течения времени" (другими словами, предоставить
язык и образы для обсуждения того, что обычно подразумевают под "природой
времени")
-описывать изменчивость широкого круга систем, ответить на вопрос оспецифичности
времени для систем различного происхождения или о егоуниверсальности.
-решить основную проблему динамического описания систем - вывод
закона изменчивости, или уравнения обобщенного движения системы (замечу, что
уравнение движения есть описание изменчивости интересующего исследователя
объекта с помощью эталонной изменчивости, т.е. часов; таким образом, от
адекватного предмету исследования выбора часов зависит способность
"увидеть" законы изменчивости)
-обсуждать свойства времени, например его субстанциональность илиреляционность,
дискретность илинепрерывность, размерность, "плотность", равномерность хода, существование
вневременных событий и т.д.
-связать возникающие представления с существующим понятийным базисомнауки (требуемое
конструирование неизбежно должно коснуться не толькопредставлений о времени, но и иных
базовых общенаучных понятий, например, пространства, движения, взаимодействия, энтропии и т.д.)
-решить так называемый "парадокс времени" (Пригожин, Стенгерс,1994): противоречие между
безусловной обратимостью во времени фундаментальныхзаконов естествознания и феноменом
становления в природе, т.е. явным различием между прошлым и будущим в мире реальных процессов.
-избавить естествознание от жупела "тепловой смерти", т.е.разрешить еще одно (не всегда
отчетливо рефлексируемое) противоречие междудействующим в замкнутой Вселенной вторым законом
термодинамики и отсутствием в Мире следов деградации и неизбежного движения к равновесию
(Ландау, Лифшиц,1964; Козырев, 1963)
Исходные принципы и гипотезы
В основе предлагаемых построений лежит ряд аксиоматических конструкций,
базирующихся на неопределяемых в предлагаемом подходе понятиях теории
множеств и теории систем – элемент, объект, изменчивость, уровень
иерархического строения заданной глубины и т.п. (Левич, 1986; 1988; 1996;
Levich 1995b).
Принцип иерархичности: все естественные системы иерархичны – любой
объект оказывается элементом системы более высокого ранга и любой
элемент оказывается системой, состоящей из элементов.
Принцип изменчивости: любое изменение системы состоит в изменении
набора элементов на определенной глубины уровнях иерархии, содержащей
систему. Наряду с термином "замена элементов" в качестве синонима
будем применять термин "субституции". Процесс замены элементов в
системе будем называть "субституционным движением" (подразумевается,
что заменяемые элементы могут принадлежать любым уровням иерархического
строения и замены могут идти как с увеличением или с уменьшением, так и с
сохранением числа частиц).
Гипотеза существования генерирующих потоков: любые естественные
системы не замкнуты по отношению к потокам элементов некоторых уровней
иерархического строения. В частности, по отношению к генерирующим
потокам открыта и наша Вселенная.
Еще ряд исходных принципов вводится в ходе изложения.
Элементы картины Мира
Имея в распоряжении генерирующие потоки, приступим к конструированию
элементов картины Мира в теории систем (Levich, 1995b, Levich, 1995c).
Назовем частицами источники или стоки генерирующих потоков в нашей
Вселенной. Некоторые частицы будут источниками (стоками) потока лишь
одного из иерархических уровней, другие частицы – одновременно
нескольких уровней. Динамические характеристики потоков порождают заряды
частиц. Потоки различных иерархических уровней порождают различные,
например, гравитационные, электрические, барионные и т.д. заряды
частиц. Источники и стоки потоков одного уровня могут соответствовать
зарядам различного знака. Моделирование частиц "входами" и "выходами"
генерирующих потоков позволяет предложть лесажевский механизм
для описания взаимодействий (Pearson, 1891; Korn, 1898; см. также Lorentz,
1901). Суть этого механизма напоминает В.И.Арнольд: "Современное
доказательство теоремы Ньютона основано на гидродинамических соображениях,
восходящих к Лапласу: дело в том, что единственное сферически симметричное
течение несжимаемой жидкости – это течение по радиусам со скоростью,
обратно пропорциональной квадрату расстояния от центра... Итак, силовое
поле притяжения точечной массой математически совпадает с полем скоростей
несжимаемой жидкости" (Арнольд, 1987). Элементы генерирующих потоков и
частицы приобретают различный бытийный статус. Частицы имеют заряды, массы,
участвуют во взаимодействиях, т.е. образуют то, что идентифицируется как
вещество, субстраты. Элементы потоков не имеют зарядов (но порождают их
у частиц), являются переносчиками взаимодействий и, возможно, могут быть
идентифицированы с полями. Предлагается называть совокупность элементов
генерирующих потоков субстанцией.
Модели с рождением вещества во Вселенной интенсивно обсуждаются в астрофизике
уже около полувека. В свете современных наблюдательных астрофизических данных
эти модели получили новый импульс (Hoyle et al., 1993).
И. Пригожин (Prigogine et al., 1987; Пригожин, Стенгерс, 1994) считает модель
с порождением вещества из гравитационной энергии (или из
пространства-времени) и открытость Вселенной как системы неизбежными для
решения парадокса времени.
Генерирующие потоки порождают становление: различие между прошлым и
будущим системы состоит в различном количестве в ней субстанции
соответствующего иерархического уровня. (Замечу, что субституционный подход
предполагает принцип конечности: естественные системы включают конечное
число элементов любого иерархического уровня. Конечно и число частиц во
Вселенной.) Признание генерирующих потоков снимает оппозицию второго начала
термодинамики существованию феноменов развития, поскольку второе начало
относится исключительно к изолированным системам и становится неприложимым
к той открытой части Вселенной, где генерирующие потоки порождают течение
времени. В замкнутой Вселенной примерно через сто тысяч миллиардов лет
погасли бы последние звезды, вещество остывших звезд, разреженного газа,
испарившихся черных дыр медленно распалось бы и во всей Вселенной остались бы
только редкие электроны и позитроны, разбросанные на гигантских расстояниях
друг от друга (Новиков, 1990). Перспективу угасания Мира можно было бы
назвать принципом Хроноса – бога, пожиравшего своих детей. Принятие
генерирующих потоков меняет взгляд на эволюцию нашего Мира, избавляя его от
жупела тепловой смерти, небытия, распада и порождая самоорганизацию и
усложнение. Альтернативу принципу Хроноса стоило бы назвать принципом
Козырева, согласно которому в самых основных свойствах материи,
пространства, времени должны заключаться возможности борьбы с тепловой
смертью с помощью противоположных процессов, которые могут быть названы
процессами жизни (Козырев, 1963).
Распространение генерирующего потока по отношению к частицам-источникам
оказывается двух "знаков" – испускание и поглощение. Выделенное
направление потока, кроме течения времени, порождает неравноправность
правых и левых систем координат, а также различные знаки зарядов.
Мысленная операция "обращения" потока должна приводить к трем
согласованным эффектам: к обращению направления времени (несоблюдение
"временной четности"), к замене правых систем координат левыми или
наооборот (несоблюдение "пространственной четности") и к замене
знака заряда частиц (изменение "зарядовой четности"; античастица,
как принято в квантовой электродинамике, оказывается частицей,
движущейся "против времени"). Обращение генерирующего потока (и
соответствующее согласованное изменение зарядовой, пространственной и
временной четностей) не меняет состояния Мира.
Вопрос об обратимости времени сводится к вопросу об обратимости генерирующих
потоков. Появление в
фундаментальных уравнениях источников материи и запрет на обратное
превращение частиц в энергию (аналогично запрету перехода тепловой энергии от
менее нагретых тел к более нагретым в термодинамике), по Пригожину (Пригожин,
Стенгерс, 1994), решают парадокс необратимости времени на фундаментальном
уровне.
Один из глубинных уровней иерархического строения исследуемой системы,
на котором есть генерирующий поток, назовем времяобразующим. Любой акт
замены элемента на произвольном более высоком, чем времяобразующий,
уровне нашей системы назовем событием. Количество элементов
генерирующего потока времяобразующего уровня, замененное между двумя
событиями в исследуемой системе, назовем интервалом субституционного
времени. Подчеркну, что выбор времяобразующего уровня произволен и
определяется волей и целями исследователя. При этом шкалы
субституционного времени, определямые различным выбором, могут
оказаться друг относительно друга неравномерными. Точнее, промежутки
времени, одинаковые в одной шкале, могут оказаться неравными при
измерении их в другой (подразумевается принятым принцип
императивности: интервалы субституционного времени между заменами
одного элемента времяобразующего уровня равны между собой и равны
единице). Таким образом, субституционное время как феномен
изменчивости объектов Мира порождается выделенным генерирующим потоком
и прарметризуется количеством элементов этого потока. Субституционные
времена, задаваемые эталонами из различных уровней строения систем и, тем
более, из различных естественных иерархий не универсальны, а
системоспецифичны. Чем более глубинен времяобразующий уровень, тем для
большего набора включающих его систем он может быть общим и порождаемая им
шкала времени – универсальной. Субституционное время дискретно (в той мере,
в какой дискретны элементы времяобразующего уровня системы), равномерность
его хода – относительна.
События на времяобразующем и на более глубоких уровнях строения систем
оказываются вневременными (замечу, что уже в квантовой механике
существуют вневременные – "мгновенные" – события: поглощеие и
испускание электромагнитных квантов атомами, редукция волнового пакета,
изменение квантовых чисел одной из частей системы в результате измерения
над другой сколь угодно далеко удаленной ее частью – парадокс
Эйнштейна-Подольского-Розена).
Объединение субстанций всех генерирующих потоков на уровнях,
расположенных выше времяобразующего, порождает пространство, в котором
существуют и взаимодействуют объекты. Пространство оказывается
субстанциональной (но не субстратной) средой. Наглядным образом
пространственного строения частиц будут не вихри или торы, а источники
("ключи", "фонтаны", "струи"), бьющие в водоеме-среде.
Последовательности "излученных" частицами элементов потока образуют
систему окрестностей частицы, порождают понятие "близости" в
пространстве и конструкции топологии и метрики в нем. Как и интервалы
времени, предлагается параметризовать пространственные измерения
количеством элементов соответствующих иерархических уровней. Вместе с
произволом в выборе времяобразующего уровня у исследователя сохраняется
произвол в выборе уровней, порождающих пространство (принцип
конвенциональности).
Принцип субституционного движения: любое движение системы состоит в
замене составляющих ее на определнном уровне строения элементов, т.е.
представляет собой вид изменения системы, или субституционное движение.
Замечу, что субституционное движение объектов в пространстве происходит не
путем "раздвигания" элементов субстанции, а путем "проникновения"
этих элементов в объекты и замене уже имеющихся в объекте
элементов, т.е. "эфирного ветра", "эфирного трения" не существует, и
субстанция генерирующих потоков в указанном смысле не является "эфиром"
XIX века. Удачным наглядным образом
субситуционного движения может быть "бегущая строка", объекты-знаки
которой движутся, благодаря "вхождению" и "выходу" из них
ламп-"точек" функционирующей "среды". Подчеркну, что принцип субституционного
движения чрезвычайно важен для предлагаемой модели – он позволяет
избавиться от многих трудностей, возникающих в моделях непустого
пространства.
Предложенная методология может быть приложена далеко не только к физическим
системам. Молекулярные или субстанциональные генерирующие потоки могут
порождать обобщенное движение на биологических, геологических, социальных,
экономических и др. уровнях иерархического строения систем (некоторые примеры
см. в ранних работах автора, Левич 1988, Levich, 1995b). Субституционное
движение выступает конструктом "обобщенного" движения и для систем
нефизического происхождения (например, геологические преобразования,
эмбриогенез и онтогенез, сукцессии и эволюции, этногенез и т.п.).
Определения пространственных и временных интервалов, а также аналогов
энергии, импульса для многоуровневых систем в приложении к субституционному
движению позволяют получить уравнения субституционного движения, порождающее
свойства нелокальности движения, существования предельной скорости движения,
неинвариантности к обращению времени, существования дополнительных к
классическим сил и др. (Levich, 1995b).
Гипотеза генерирующих потоков допускает и радикальные предположения о
специфике явлений жизни: так же как частицы-заряды являются источниками
генерирующих потоков, порождающих физические взаимодействия, так и живые
организмы есть источники специфических потоков предэлементов каких-то
иерархических уровней строения материи. Различные потоки могут быть
ответственны за свойства жизни, сознания, пассионарности (о пассионарности
см., например, работу Л.Н.Гумилева, 1989). Свойства жизни по своему
происхождению становятся аналогичными свойствам, например, электрического или
барионного заряда. Отличие живого от неживого
оказывается связанным со специфичностью и количеством клеточных
генерирующих потоков. Искушенный читатель может увидеть в гипотетических
субстанциональных потоках субституционного подхода возрождение жизненных
сил витализма. Однако утверждения субституционной концепции значительно
прозаичнее: речь идет о вполне материальных, но не регистрируемых
средствами современных научных технологий уровнях строения естественных
систем. Гипотетические потоки предэлементов этих уровней нужны не
специально для введения жизненных сил, а отвечают логике вывода
субституционным подходом целого круга научных конструкций в естествознании.
Энтропийная параметризация субституционного времени
Измерение пространственных и временных интервалов в субституционном подходе
подразумевает осуществление процедуры подсчета количества элементов. Подсчет
элементов в структурированных математических объектах, эксплицирующих
естественнонаучные объекты при их формальном описании, требует обобщения
понятия количества. Один из путей такого обобщения дается функторным методом
сравнения математических структур в методологии категорно-функторного
описания систем (Левич, 1982; Левич, Соловьев, 1996). Аналогом количества
элементов бесструктурного множества для объектов с заданной математической
структурой служит инвариант математической структуры – количество морфизмов данной структуры.
Инварианты большинства математических структур выражаются через инварианты структуры множества
с разбиением, ассоциированным с данной
произвольной структурой. Логарифмы инварианта структуры множеств с
разбиениями имеют типичный энтропиеобразный вид. Например, если морфизмы,
сохраняющие структуру множеств с разбиениями, есть отображения, то логарифм
удельного инварианта есть ![]() , где ni – количества элементов в
, где ni – количества элементов в
классах разбиения, ![]() , w есть число классов разбиения. Предлагается
, w есть число классов разбиения. Предлагается
использовать энтропийные инварианты при параметризации субституционного
движения сложных объектов естествознания. Правда, такое использование требует дополнительных
предположений о законах, порождающих описание движения.
Экстремальный принцип субституционного движения
Предлагается экстремальный принцип для отбора реального движения из
спектра всех потенциально допустимых структурой системой движений: из
заданного состояния системы осуществляется переход в то состояние, для
которого логарифм инварианта структуры системы максимален в пределах
субстанциональных ограничений, обусловленных порождающими изменчивость
системы генерирующими потоками.
В силу экстремального принципа логарифм инварианта системы вдоль реальных
траекторий не убывает и может, тем самым, играть роль параметрического
времени системы, из-за чего и назван ее "энтропийным временем".
Рассмотрим пример многоуровневого субституционного объекта со структурой
разбиения множества элементов верхнего уровня на классы и генерирующими
потоками предэлементов глубинных уровней. Зафиксируем времяобразующий
уровень нашей системы глубины ![]() . В силу экстремального принципа
. В силу экстремального принципа
движение рассматриваемого объекта описывается следующей вариационной
задачей:
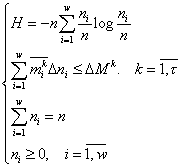
Здесь ni – количество элементов в классе разбиения i,
![]() – среднее количество предэлементов уровня k в элементах класса i,
– среднее количество предэлементов уровня k в элементах класса i,
![]() – прошедшее через систему количество субстанции генерирующего потока
– прошедшее через систему количество субстанции генерирующего потока
![]() уровня k за субституционное время
уровня k за субституционное время ![]() .
.
Если ![]() , то система замкнута,
, то система замкнута,
экстремальный принцип приводит к равновесному состоянию и эквивалентен
второму началу термодинамики. Наличие же генерирующих потоков влечет
образование структур и самоорганизацию систем.
Можно показать (Левич и др., 1994), что для энтропийного времени системы
H выполняется
![]()
где ![]() – множители Лагранжа вариационной задачи (1), и
– множители Лагранжа вариационной задачи (1), и
что ![]() ,
,
т.е. энтропийное H и субституционное ![]() времена системы монотонны,
времена системы монотонны,
благодаря чему обретает право
существования декларированный выше тезис о возможности энтропийной
параметризации субституционного времени. Замечу, что согласно формуле (2)
энтропийное время оказывается "усреднителем" различных субституционных
времен. Также эта формула демонстрирует связь энтропийного времени с
обычной термодинамической энтропией: если один из потоков ![]() есть
есть
поток тепла ![]() , то соответствующий множитель Лагранжа обычно
, то соответствующий множитель Лагранжа обычно
обозначается 1/T, где T абсолютная температура системы, и
соответствующий член в сумме приобретает вид термодинамической энтропии
![]() .
.
Для задачи (1) выполняется теорема стратификации (Левич и др., 1994):
пространство системы
![]() разбивается на
разбивается на ![]() областей, в
областей, в
каждой из которых решение задачи (1) зависит от генерирующих потоков одного
из непустых подмножеств полного набора уровней ![]() . Для
. Для
потоков из этого подмножества в соответствующей подмножеству области
пространства некоторые неравенства из задачи (1) становятся равенствами, а
для уровней, не входящих в рассматриваемое подмножество – строгими
неравенствами. Другими словами, в каждой области пространства системы ее
движения определяется некоторыми из генерирующих потоков и не определяется
другими. Если генерирующие потоки различных уровней иерархического строения
системы порождают различные типы взаимодейтсвия частиц, то эти взаимодейтсвия
проявляются в различных областях пространства системы.
Для задачи (1)
выполняется теорема о максимуме обилия классов: численности классов ni
зависят только от отношений количеств ![]() ; наибольшего своего
; наибольшего своего
значения численность ni достигает при отношении
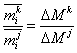
(Левич и др., 1993).
Экстремальный принцип может интерпретироваться как принцип наибольшей
структурированности системы, наибольшей ее сложности, максимума энтропии.
Возможна еще одна – субстанциональная – интерпретация экстремального
принципа. А именно, для вариационной задачи (1) справедлив аналог теоремы
Гиббса, согласно которому задача на максимум энтропии с ограничениями сверху
генерирующими потоками эквивалентна задаче на минимум любого из генерирующих
потоков с ограниченями снизу на структурный инвариант системы. Т.е.
экстремальный принцип приобретает смысл минимального "потребления"
генерирующей субстанции или минимального субституционного времени.
Предложенная вариационная задача позволяет моделировать системы в экологии
сообществ (Левич, 1980; Левич, 1982; Левич и др., 1993; Левич и др., 1994;
Левич и др., 1996): рассчитывать численности популяций как функции ресурсов
среды; выявлять факторы, лимитирующие развитие сообществ; рассчитывать
потребления популяциями ресурсов среды и потребности в них; управлять
структурой и функциями сообществ с помощью потоков ресурсных факторов.
Модель(1) может оказаться полезной в исследовании экономических систем для
расчета распределения продуктов производства в зависимости от обеспеченности
различными материальными, энергетическими, финансовыми, трудовыми и др.
ресурсами и от потребностей в них, для выявления лимитирующих рост
производства ресурсов в пространствах ресурсов большой размерности, для
оптимизации распределения продуктов по различным критериям с помощью
соотношений ресурсов, ограничивающих рост.
Заключение
По отношению ко времени модель в определенной степени снимает
оппозицию между реляционными и субстанциональными подходами. Дело в том, что
традиционные реляционные модели времени (см., например, Аристов, 1994)
постулируют
частицы материи и их движение, время же становится конструктом теории.
Описываемый подход возлагает ответственность за феномен времени на субстанцию
одного из уровней иерархического строения систем (если угодно – та же
материя, но в специфической форме), движение постулируется принципом
изменчивости, а субституционные часы и феномен становления становятся
конструктами теории. Т.е. реляционный и субстанциональный подходы оказываются
схожими по своей структуре, только первый из них имеет дела с материальными
объектами в известной форме, а второй – с материей, не идентифицируемой
пока современными научными технологиями.
Гипотеза существования генерирующих потоков в значительной степени радикальна.
Сдержанно настроенному читателю можно предложить рассматривать гипотезу
потока лишь как удобное средство описания и моделирования феноменов
становления, течения времени, развития. Т.е., если угодно, перевести
представления о потоке из области онтологии в методы гносеологии.
Резюмирую, что феномен времени в предложенном подходе тривиализуется до
имманентного свойства открытых систем: изменчивость систем, порождается и
параметризуется потоками субстанций, по отношению к которым открыта
исследуемая система.
ЛИТЕРАТУРА
1.Аристов В.В. Статистическая модель часов в физической теории //
Доклады РАН. 1994. Т.334. N. 2. С.161--164.
2.Арнольд В.И. Трехсотлетие математического естествознания и небесной
механики // Природа. 1987. N. 8. С.5--15.
3.Гумилев Л.Н. Этногенез и биосфера Земли. Л.: Наука. 1989.
4.Козырев Н.А. Причинная механика и возможность экспериментального
исследования свойств времени // История и методология естественных наук.
Вып. 2. М.: 1963. С.95--113.
5.Ландау Л.Д., Лифшиц Е.М. Статистическая физика. М.: Физматгиз.
1964. С. 45-46.
6.Левич А.П. Структура экологических сообществ. М.: Изд-во Московского
университета. 1980.
7.Левич А.П. Теория множеств, язык теории категорий и их применение в
теоретической биологии. М.: Изд-во Московского университета. 1982.
8.Левич А.П. Тезисы о времени естественных систем // Экологический
прогноз. М.: Изд-во Московского университета. 1986. С. 163--190.
9.Левич А.П. Метаболическое время естественных систем //
Системные исследования. Ежегодник 1988. М.: Наука. 1989. С.304--325.
10.Левич А.П. Научное постижение времени // Вопросы философии. 1993. N. 4.
С.117--126.
11.Левич А.П. Субституционное время естественных систем // Вопросы
философии. 1996. N. 1. С.57--69.
12.Левич А.П., Алексеев В.Л., Рыбакова С.Ю. Оптимизация структуры
экологических сообществ: модельный анализ // Биофизика. 1993. Т.38. Вып.5.
С.877--885.
13.Левич А.П., Алексеев В.Л., Никулин В.А. Математические аспекты
вариационного моделирования в экологии сообществ // Математическое
моделирование. 1994. Т.6. N. 5. С.55--71.
14. Левич А.П., Соловьев А.В. Категорно-функторное моделирование
естественных систем // Статья в настоящем сборнике.
15. Левич А.П., Максимов В.Н., Булгаков Н.Г. Экспериментальная и
теоретическая экология фитопланктона: управление структурой и функциями
сообществ. Учебное пособие. М.: Изд-во Московского университета. 1996.
16. Пригожин И., Стенгерс И. Время, хаос, квант. М.: Прогресс. 1994.
17.Hoyle F., Burbidge G. and Narlicar I.V. A Quasi-Steady State
Cosmological Model with Creation of Matter // The Astrophysical J. 1993. V.
410. Pp.437--457.
18.Korn A. Eine Theorie der Gravitation und der elektrischen
Erscheinungen auf Grundlage der Hydrodynamik. Berlin. 1898.
19. Levich A.P. Motivations and problems of studying time // On the Way to
Understanding the Time Phenomenon: the Constructions of Time in Natural
Science. Part 1. Interdisciplinary Time Studies. L.: World Scientific. 1995a.
Pp. 1--16.
20.A.P.Levich. Time as Variability of Natural Systems: Ways of
Quantitative Description of Changes and Creation of Changes by
Substantial Flows // On the Way to Understanding the Time Phenomenon: the
Constructions of Time in Natural Science. Part 1. Interdisciplinary Time
Studies. L.: World Scientific. 1995b. Pp. 149--192.
21.Levich A.P. Generating flows and a substantional model of space-time //
Gravitation \& Cosmology. 1995c. V.1. N. 3. Pp. 301--306.
22.Lorentz H.A. Aether theories and aether models. Ed. H.Bremekamp. 1901.
23.Pearson K. Ether Squirts // Amer. J. of Math. V.13. 1891. P. 309.
24.Prigogine I., Geheniau J., Gunzig E., Nardone P. Thermodynamics and
Cosmology //General Relativity and Gravitation. 1989. V.21. P. 1.
Study of Time IV. Proc. 4th Conference of the International Society for
the Study of Time. N.Y. 1981.