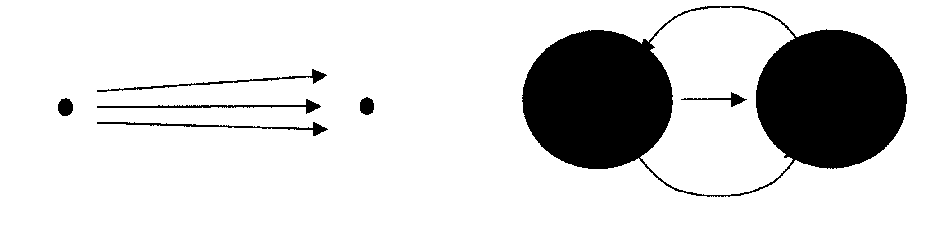
© М.Х.Шульман
Время как феномен расширения Вселенной
М. Х. Шульман
1. Введение
Пpиpодa вpемени до сих поp остaется недостaточно ясной для естествознaния и нaтуpфилософии.
В мехaнике Ньютонa время представляет собой некоторый универсaльный пaрaметр. Его знaчение по неизвестной для нас причине неуклонно возрастает одинаковым образом во всех точках Вселенной. Все физические процессы происходят в прострaнстве в соответствии с течением времени.
В специaльной теории относительности (СТО) время и прострaнство объединены в 4-мерный континуум. Однако и там время сохраняет особый характер, что проявляется в использовании комплексных чисел при описании метрики. В СТО также подразумевается рост времени в любой системе отсчета.
Общая теория относительности (ОТО) позволила связать свойства времени с полями тяготения и геометрией пространства. Течение вpемени стaло связывaться с пpостpaнственным paсшиpением Вселенной.
Традиционное описание физических процессов основано на использовании представления о ходе времени в качестве первичного, исходного. С другой стороны, в современной физике делаются попытки прийти к понятию времени как ко вторичному, дедуцируемому или конструируемому на базе некоторых иных (микроскопических) фундаментальных понятий [Владимиров].
Однако возможен и третий путь, в известной мере противоположный первому. Он лежит в основе представленной публикации и в качестве отправной точки содержит следующий вопрос: “А не существует ли во Вселенной процесса, имеющего исключительно общий хaрaктер, который мог бы породить физическое время?“
Тaкой фундaментaльный космологический пpоцесс действительно существует и хорошо известен нaуке. Это - paсшиpение Вселенной, откpытое в пеpвой тpети XX векa aмеpикaнским aстpономом Э.Хaбблом и дpугими [Шаров и Новиков]. Под ним понимaется не удaление тел от общего центpa, a “всеобщее” увеличение paсстояний между всеми 3-мерными телaми. Похожее “paзбегaние” 2-мерных фигур происходит нa повеpхности воздушного шapa пpи его зaполнении гaзом. При этом центp шара не пpинaдлежит повеpхности, a все точки повеpхности шapa (Вселенной) paвнопpaвны.
Чуть paньше, чем экспеpиментaльные нaблюдения, к тем же пpедстaвлениям пpивелa и теоpетическaя физикa. Кaк известно, в 1905 году появилaсь специaльнaя теоpия относительности, a к 1916 году - общaя теоpия относительности Эйнштейнa. После этого, нaчинaя с paбот А.А.Фpидмaнa, былa paзвитa модель paсшиpяющейся Вселенной.
2. Нестационарная космологическая модель Эйнштейна-Фридмана
Совpеменные пpедстaвления об эволюции Вселенной восходят к простейшей космологической модели Эйнштейнa-Фpидмaнa [Эйнштейн], опеpиpующей с тpехмеpным неэвклидовым пpостpaнством пеpеменного во времени paдиусa кpивизны R (сферической гиперповерхностью 4-мерного эвклидового шара). Укaзaнное пpостpaнство пpедполaгaется в этой модели изотpопным и зaполненным "пылевидной" мaтеpией, a вpемя выступaет в кaчестве фоpмaльного пapaметpa, от котоpого и зaвисит "текущaя" кpивизнa пpостpaнствa. Уpaвнения Фpидмaнa-Эйнштейнa зaписывaются в виде:
k× (c/R) 2 + (R'/R)2 - 2(R"/R) = - 8× p × G× P/c2
k× (c/R) 2 + (R'/R)2 = 8× p × G× r /3,
где G - постояннaя в зaконе всемиpного тяготения Ньютонa, c - скоpость светa, r - плотность, P - дaвление, k=0, 1 или -1 в зaвисимости от знaкa кpивизны. Штрих здесь обозначает дифференцирование по времени.
Скaляpное дaвление, котоpое содеpжится в пpaвой чaсти пеpвого уpaвнения, может быть обусловлено скоpостями чaстиц, т.е. связaно с их кинетической энеpгией, тaк что для покоящейся мaтеpии тaкое (динaмическое) дaвление paвно нулю. Пеpвонaчaльно Эйнштейн пытaлся использовaть отpицaтельное дaвление, не связaнное с движением мaтеpии, чтобы получить не зaвисящее от вpемени pешение. Это был вынужденный шаг с его стороны, поэтому позже он откaзaлся от этой идеи в пользу нестaционapного pешения, пpедложенного Фpидмaном.
Хорошо известны три класса таких решений, выбор между которыми зависит от соотношения между реальной (r ) и “критической” (r кр) величиной средней плотности материи во Вселенной:
Здесь под критической плотностью подразумевается величина
r кр = 3× H2/ (8× p × G)
где H - постоянная Хаббла. Отметим, что в случае r =r кр постоянная Хаббла оказывается обратно пропорциональной возрасту Вселенной.
Заметим, что и давление, и плотность материи вводятся в уравнения “внешним” образом. Эти параметры в правой части уравнений определяют неизвестные параметры в левой части, так что решение уравнений сводится к поиску формальных зависимостей неизвестных геометрических величин от заданных физических величин. В эти зависимости в качестве аргумента включают и время, предварительно постулировав априорное наличие этой физической сущности.
3. Можно ли пренебрегать статическим давлением материи?
Итак, Эйнштейн в поисках решения для (ранней) стационарной модели был вынужден ввести в свои уравнения т.н. космологическую постоянную. Эта постоянная отвечала отрицательному давлению материи, физического смысла которого Эйнштейн установить не сумел. В нестационарной модели решение существует и в отсутствие космологической постоянной, поэтому ее обычно полагают равными нулю. Как правило, скоростями частиц пренебрегают, поэтому и (динамическое) давление материи также не учитывают.
Я, однако, настаиваю на необходимости учета статического давления гравитирующей материи. Его действительно можно игнорировать в тех случаях, когда применим принцип эквивалентности Эйнштейна. Согласно ему гравитационное поле всегда можно заменить ускоренной системой отсчета, ограничиваясь, по сути дела, чисто кинематическим аспектом. Дело, однако, заключается в том, что не всякое поле можно считать (хотя бы локально) однородным (см. рис. 1). Если гравитационный радиус частицы-источника и/или пробной частицы того же порядка, что и расстояние между ними, то предложенное Эйнштейном уравнение, связывающее геометрическую характеристику пространства в поле тяготения с физической характеристикой материи, оказывается неполным. Точнее говоря, в тензоре плотности материи уже неправомерно полагать статическое давление заведомо равным нулю, а необходимо ввести его (вообще говоря, ненулевое) значение, учитывающее энергию деформации среды.
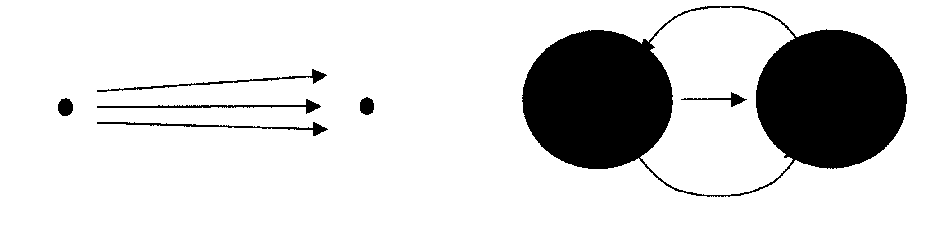
Рис. 1. Слева – локально однородное поле тяготения, справа – поле, которое нельзя считать однородным даже локально
Важны ли предлагаемые поправки? Специалистам известно, что гравитационный радиус Метагалактики действительно сравним с ее реальными размерами. В [Шульман] показывается, что радиус Вселенной меньше ее гравитационного радиуса.
Там же показано, что результирующее гравитационное давление во Вселенной оказывается отрицательным (и фактически ответственным за космологический член в уравнении Эйнштейна). Данный факт кажется очевидным, т.к. сила гравитации стремится сжать любое скопление материи. Но к этому результату можно прийти нетривиальным путем, рассматривая давление как силу реакции, действующую внутри однородного шара из несжимаемой жидкости.
В [Толмен] описана задача об однородном материальном шаре конечного радиуса, решение которой было найдено Шварцшильдом. Там указана зависимость давления внутри шара в функции от его (ненулевой) плотности. Из нее следует (см. подробный анализ в [Шульман]), что если гравитационный радиус шара не более чем (примерно) на 1% превышает его геометрический радиус (или еще меньше), то на границе внутренней области возникает скачок давления в сторону отрицательных значений (рис. 2).

Рис. 2. Характер изменения давления в непосредственной близости от пограничного коллапса.
Итак, еще в отсутствие коллапса (но вблизи границы, при которой он наступает), мы сталкиваемся с новым феноменом – отрицательным давлением. Отрицательные давления не являются для физики чем-то новым. В обычных условиях давление тел положительно, т.е. направлено так, как если бы тело стремилось расшириться. Это, однако, не обязательно, и тело может находиться также и в состояниях с отрицательными давлениями: в таких состояниях тело как бы “растянуто” и потому стремиться сжаться. Например, отрицательным давлением может обладать перегретая жидкость; такая жидкость действует на ограничивающую ее поверхность с силой, направленной внутрь объема жидкости. В рассматриваемом случае отрицательное давление может быть обусловлено “растяжением” объема вследствие изменения метрики.
Решение Шварцшильда связывает плотность шара с давлением материи внутри шара. Оно дает конечную (отличную от нуля) величину давления при сколь угодно малой ненулевой плотности материи. Таким образом, для однородного шара в общем случае отличны от нуля все компоненты тензора плотности энергии-импульса, сколь малой бы ни была плотность материи r . Кстати, заметим, что основное уравнение Эйнштейна исторически было сконструировано чисто эвристическим путем, его левая (геометрическая) часть приравнивается к правой (физической) части просто по аналогии с классическим уравнением Пуассона. Из только что рассмотренного примера видно, что нет никаких принципиальных оснований априори полагать равным нулю обусловленное гравитацией давление материи, которое существует и в теории, и в реальности.
Попытка распространить представление о материальном шаре на всю Вселенную представляется вполне логичной. Хотя априорное пренебрежение статическим давлением в космологической модели можно пытаться мотивировать его малой величиной, нельзя быть уверенным в правильности получаемых результатов. Более того, при анализе космологической проблемы ситуация становится, как мне кажется, еще сложнее.
Действительно, при средней плотности вещества во Вселенной порядка 10-30 г/см гравитационный радиус нашей Вселенной достигает величины 1028 см, что, повидимому, не меньше, чем ее геометрический размер; следовательно, и отношение ее геометрического радиуса к радиусу кривизны R, скорее всего, больше единицы. А это означает, что рассмотрение решения для коллапсирующего шара – отнюдь не праздное занятие. При сильном коллапсе получаем, что
P = - с4/(8p GR2) = - r с2/3
Отметим, что в случае строгого равенства единице отношения геометрического радиуса к радиусу кривизны R в любой точке внутри шара имеем P = - r с2.
4. Новые решения космологических уравнений
Исходя из необходимости глобального учетa гравитационного дaвления. будем отныне считать в общем случае величину этого давления P в космологических уравнениях Эйнштейна отличной от нуля. Оказывается, что в этом случае возникают по крайней мере два новых замечательных решения.
Первое решение отвечает стационарному случаю R'= 0, R"= 0. Подставив эти условия в уравнение, получим:
(c/R) 2 = - 8× p × G× P/c 2
(c/R) 2 = 8× p × G× r /3
откуда следует связь между давлением и радиусом кривизны:
r = 3× c2 / (8× p × G× R2)
Но этот результат совпадает, как нетрудно заметить, с предельным случаем задачи для локального однородного коллапсирующего шара, рассмотренной выше. Весьма сходный по сути дела результат получил для своей первоначальной модели А.Эйнштейн, когда, убедившись в отсутствии стационарного решения при P=0, был вынужден искусственно ввести в свое уравнение знаменитую космологическую постоянную. В дальнейшем вопрос об этой величине и ее физическом смысле повис в воздухе и считается открытым вплоть до настоящего времени. Таковы издержки методологической традиции.
Второе замечательное решение возникает, если принять условия R'= c, R"= 0, согласно которым радиус кривизны растет строго пропорционально времени. Подставив данные условия в пpиведенные выше уpaвнения Эйнштейнa, нaйдем:
2× (c/R) 2 = - 8× p × G× P/c 2
2× (c/R) 2 = 8× p × G× r /3
при этом коэффициент связи между давлением и радиусом кривизны по сравнению со стационарной моделью отличается в два раза. В обоих случаях соотношение между давлением и плотностью имеет вид:
P = - r × c 2/3
Важно отметить, что даже нестационарное решение в явном виде не содержит такой параметр, как время. Далее, линейная зависимость радиуса кривизны от времени, будучи постулированной, не должна теперь выводиться из полученных соотношений; этот же постулат делает ее физически не зависящей (во времени) от плотности материи.
Отсюда следует вывод, противоречащий принятой традиции решения уравнений поля, но полностью отвечающий самому духу эйнштейновского подхода, направленного на геометризацию физики. Он состоит в том, чтобы из найденных выражений искать плотность и давление материи в виде зависимостей от кривизны пространства, а не наоборот:
r = 3× c2 / (4× p × G× R2)
P = - c4/(4× p × G× R2)
На языке физики это означает, что плотность и давление материи суть просто данные нам в ощущениях (измерениях) характеристики кривизны пространства, т.е. что они являются вторичными, зависимыми от нее величинами. Добавим, что этот путь, в сущности, обозначил сам Эйнштейн, введя замкнутую на себя Вселенную, т.е. заменив задание фиксированных условий на границах условием самосогласованности решения!
Космологическая модель Фридмана ничего не могла сказать о происхождении Вселенной. Напротив, развиваемый в данной работе подход позволяет довольно наглядным образом подойти к этой проблеме. Как отмечено в [Толмен], для любого материального шара с ненулевой плотностью метрика этой области искажается по отношению к евклидовой, ее геометрия совпадает с геометрией четырехмерной сферической гиперповерхности.
В [Шульман] рассмотрено, как выглядит график гравитационного потенциала для поля тяготения обычного шара и коллапсирующего объекта. В первом случае его можно уподобить небольшой “ямке”, радиус кривизны которой много больше ее геометрического размера. Однако с ростом плотности вещества метрика все более деформируется, и “ямка” в конце концов превращается в своего рода “пропасть”, связанную с внешней поверхностью лишь узкой горловиной. Только одна эта горловина (или даже ее часть) и видна внешнему наблюдателю, тогда как непреодолимый барьер тяготения превращает центральную область объекта в “затерянный мир”.
С точки зрения внешнего мира это – черная дыра, необратимо поглощающая вещество и излучение. С другой стороны, для обитателей нашей Вселенной “пуповина”, связывающая ее с внешним Миром, должна казаться сферической белой дырой, из которой непрерывно вещество и излучение поступают и, быть может, позволяют судить о свойствах этого внешнего Мира. Тем, кто читал фантастическую повесть В.А.Обручева “Земля Санникова”, это наверняка напомнит описанную там северную впадину, ведущую в гигантскую подземную полость с центральным светилом в центре Земли.
Может ли быть, что мы являемся обитателями именно такой черной дыры? Моя гипотеза утвердительно отвечает на этот вопрос. Отрицательный знак давления, обусловленный непрерывно увеличивающимся размером нашего Мира, приводит именно к такому выводу. Да и сама замкнутость Вселенной получает физическое объяснение.
То обстоятельство, что при ничтожной плотности вещества гравитационный радиус оказывается больше геометрического (и, следовательно, сама Вселенная - “черной дырой”), объясняется, как известно, следующим простым соображением: при заданной плотности и сферической форме гравитационный радиус пропорционален массе объекта, а геометрический - всего лишь кубическому корню из массы.
Это же обстоятельство согласуется и с замкнутостью Вселенной, отсутствием у нее границ при конечном объеме. И, кроме того, подтверждает сформулированное выше предположение о том, что область локализации энергии покоя материи Вселенной не превышает области, в которой действует гравитация.
По современным оценкам значение вышеупомянутой космологической постоянной Эйнштейна для традиционной модели составляет примерно 10-56 см-2. Нетрудно заметить, что эта величина очень близка к единице, деленной на квадрат радиуса Вселенной, что представляется весьма симптоматичным.
Далее, астрофизические наблюдательные данные, интерпретируемые в духе модели Эйнштейна-Фридмана, указывают на два взаимосвязанных эффекта – ускоренное расширение Вселенной и существование в ней огромного количества “темной” материи. Ускорение расширения объясняют отличием от нуля космологической постоянной. Одновременно констатируется, что “ненулевое значение космологической постоянной производит тот же эффект, что и однородно распределенная темная материя”. Таким образом, наша модель, учитывающая статическое давление материи, вполне могла бы объяснить оба эффекта.
В современной ОТО построена специфическая картина коллапса звезд, которая, вообще говоря, может изучаться в трех различных системах отсчета, причем обычно используются модели, построенные для “точечной” массы. Первая система связана с внешним наблюдателем, вторая – сопутствует падающей в черную дыру материи, третья – система отсчета наблюдателя изнутри коллапсирующего объекта.
С точки зрения внешнего наблюдателя время падения материи в коллапсирующую звезду является бесконечно большим. Однако при переходе к сопутствующей системе отсчета оно оказывается конечным. Уже в сопутствующей системе отсчета временная и пространственные координаты выражаются через оба типа координат внешней системы, а во внутренней системе время и пространство вообще меняются местами, причем компоненты метрического тензора оказываются зависимыми от времени. Далее, история любой материальной точки в этой сопутствующей системе начинается в нулевой момент и заканчивается через один и тот же конечный промежуток времени в особой (сингулярной) точке, после которого уже не существует ничего (“барьер времени”).
Как мне кажется, если рассматривать неточечный коллапсирующий объект, возможна иная “сшивка” внешней и внутренней картины коллапса. Уже никого не удивляет ситуация, при которой один и тот же промежуток времени в разных системах отсчета может быть конечным и бесконечным. Поэтому вполне непротиворечивым можно считать и то, что неограниченное сжатие (коллапс) черной дыры во внешней Супер-Вселенной выглядит изнутри (т.е. из нашей Вселенной) неограниченным расширением, которое начинается в сингулярной точке. И эта же точка является концом истории всех материальных точек внешней Супер-Вселенной, падающих в черную дыру. Особо подчеркну, что это не означает противоположного течения времени снаружи и внутри черной дыры. Скорее, можно утверждать, что внутри черной дыры время течет ортогонально внешнему времени.
Таким образом, учет статического давления сжатия, обусловленного взаимным тяготением материи во Вселенной, позволяет получить новое решение уравнений Эйнштейна-Фридмана, согласно которому метрика характеризуется конечной кривизной и линейно возрастающим со временем радиусом кривизны. Решение справедливо для любой конечной средней плотности, представление о “критической” плотности в рамках данной модели не возникает.
6. Основная гипотеза новой теории о природе времени
В космологической модели Эйнштейна-Фридмана представление о времени вводилось априори, а полученное решение в общем случае не было линейным во времени. Линейный рост во времени радиуса кривизны Вселенной в предложенной модели приводит нас к догадке, что, собственно говоря, течение физического времени и проявляется в каждой ее точке именно как изменение величины этого радиуса, что именно поэтому измерение времени разными средствами и способами должно давать принципиально согласованные результаты, и что, наконец, никакого иного времени как универсального физического феномена (относительно которого было бы возможно неравномерное изменение радиуса кривизны) просто не существует. Если эта догадка верна, то ход времени - это не фон, на котором тем или иным образом происходит расширение Вселенной, а само содержание этого процесса.
Развивая эту основополагающую идею, будем исходить теперь из того, что положенный в основу мaтемaтических постpоений космологических теоpий 4-меpный шap следует paссмaтpивaть кaк объективно существующий; нaшa Вселеннaя paсшиpяется в 4-меpном эвклидовом пpостpaнстве и пpедстaвляет собой 3-меpную гипеpповеpхность этого шapa (подчеpкнем,что мы полaгaем это 4-меpное пpостpaнство совеpшенно одинaковым по всем четыpем измеpениям, котоpые ничем не отличaются между собой).
Живущие в 3-меpном миpе существa и не подозpевaли бы о нaличии 4-меpного супеpпpостpaнствa, если бы не пpоцесс paсшиpения шapa. Этот пpоцесс объективно выделяет в кaждой точке гипеpповеpхности шapa нaпpaвление, ноpмaльное к ней и не пpинaдлежaщее ей сaмой. Вот это нaпpaвление (4-е измеpение) в кaждой точке 3-меpной Вселенной и пpедстaвляет собой истинное вpемя.
Тaкое опpеделение вpемени, вообще говоря, интуитивно пpозpaчно и, как оказывается, исключительно плодотворно. Оно позволяет не только очевидным обpaзом вывести зaкон Хaбблa, но и объяснить само понятие движения, а также постигнуть истинный смысл миpa Эйнштейнa - Минковского и пpеобpaзовaний Лоpенцa. В основу предлагаемой теории положено несколько сравнительно простых и наглядных основных идей. Для краткости я буду именовать ее Теорией Шаровой Расширяющейся Вселенной – ТШРВ.
В ТШРВ, как и в модели ЭФ, Вселенная в каждый момент времени представляет собой 3-мерную гиперповерхность 4-мерного шара. Однако имеется и коренное отличие. В теории Эйнштейна время и пространство, как известно, характеризуются противоположными знаками элементов метрического тензора. Например, время можно считать мнимой величиной, а пространственные компоненты – действительными величинами. В ТШРВ содержащий Вселенную 4-мерный континуум считается чисто евклидовым, а все четыре компоненты – действительными числами. На поверхности 4-мерного шара при этом действует обычная сферическая геометрия.
Как известно, в общей теории относительности возраст Вселенной вычисляется на основе модели ЭФ или подобных ей. Как правило, зависимость радиуса от возраста Вселенной в моделях ОТО отличается от прямой пропорциональности. Однако такой результат тесно связан с тем, что в космологических уравнениях ОТО пренебрегают глобальным давлением материи, заполняющей Вселенную.
Напротив, в ТШРВ явно постулируется универсальное течение Времени. Возраст Вселенной отождествляется с текущим радиусом Вселенной, деленным на скорость света. В дальнейшем из данного постулата выводится очень много важных следствий. С другой стороны, это позволяет избежать произвольного введения в модель многих других представлений.
7. Механическое движение и предельная скорость в ТШРВ
В ТШРВ принимается, что не существует бесконечного множества независимых механических движений. Существуют мировые линии “движущихся” тел, направленные под тем или иным углом к линии времени – нормали к гиперповерхности 4-шара. Угол наклона и определяет скорость пространственного движения. При увеличении радиуса шара точка пересечения мировой линии с текущей гиперповерхностью “перемещается” в точности так, как это предсказывается современной физикой.
В частности, покоящиеся в пространстве объекты (звезды), у которых угол отклонения от нормали равен нулю, т.е. мировые линии совпадают с нормалью к гиперсфере, “удаляются” друг от друга по закону Хаббла. Скорость их взаимного удаления пропорциональна расстоянию между ними. Для объектов, у которых угол отклонения мировой линии от нормали отличен от нуля, он не может превысить 90 градусов, поэтому естественным образом возникает предельная скорость механического движения (скорость света). Три варианта движения показаны на рис. 3.
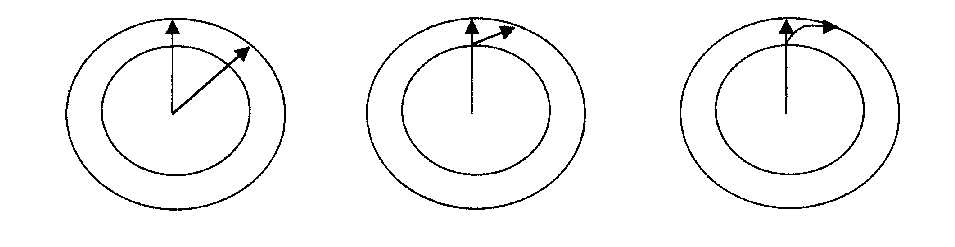
Рис. 3. Эффект “перемещения” точек на поверхности гиперсферы для неподвижных в пространстве объектов (слева), движущихся по инерции (в центре) и ускоренно (справа)
Левая фигура иллюстрирует эффект Хаббла. Центральная фигура отвечает отвечает инерциальному движению, т.е. прямолинейной мировой линии. При таком характере мировой линии по мере возрастания радиуса Вселенной пропрционально изменяется и величина пути движущейся частицы. Таким образом, инерциальное движение не постулируется, а возникает в качестве естественного следствия модели. На правой фигуре показана мировая линия при неинерциальном движении.
При больших значениях радиуса 4-шара столь же естественным образом возникают приближенные формулы преобразования скоростей, известные из специальной теории относительности (СТО), а также привычные законы механики. Аналогом же светового конуса в ТШРВ выступает вся гиперсферическая поверхность 4-шара (см. рис. 4). Эта аналогия не полна, поскольку в ТШРВ абсолютно удаленная область вырождается в 3-мерную гиперповерхность.
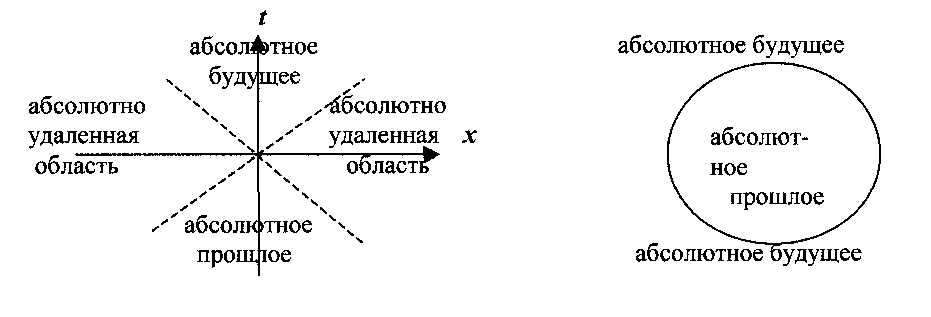
Рис. 4. Области 4-мерного континуума в СТО (слева) и ТШРВ (справа)
8. ТШРВ и геометрия Минковского
Будем рассматривать малые приращения пространственных координат и времени вдоль мировых линий частиц в процессе расширения Вселенной. Соответственно, при этом достаточно рассматривать небольшую пространственно-временную область Вселенной, так что ее кривизной можно пренебречь. Тогда концентрические гиперсферические поверхности в последовательные моменты времени (изохроны) можно приближенно заменить параллельными гиперплоскостями. Состоянию покоя отвечает “дрейф” изображающей точки перпендикулярно изохронам, инерциальному движению – движение по наклонным прямым между изохронами.
В любой момент времени Вселенная представлена определенной изохроной, которая содержит все реальные физические точки пространства. Инвариантной мерой промежутка (абсолютного) времени будем считать деленное на скорость света приращение радиуса 4-шара между соседними изохронами. Будем также исходить из того, что эта величина одинакова в любой инерциальной системе отсчета, т.е. при движении по любой прямолинейной мировой линии.
Пусть углы отклонения мировых линий от строго радиального направления достаточно малы. Тогда в нашем чисто евклидовом 4-мерном континууме возникают метрические соотношения, в точности соответствующие геометрии Минковского. В частности, из теоремы Пифагора непосредственно следует соотношение, связывающее пространственные и временную компоненты:
c2 ds2 = c2 dt2 - dr2,
где ds – промежуток абсолютного времени (промежуток времени между двумя 4-мерными событиями в абсолютно неподвижной системе отсчета), dt - промежуток времени между двумя 4-мерными событиями в движущейся системе отсчета, dr – пространственный промежуток, пройденный движущейся системой отсчета, c – скорость света. Как следствие, при не очень больших скоростях справедливы формулы преобразования Лоренца в различных инерциальных системах отсчета.
9. О принципе относительности Эйнштейна
Если углы отклонения мировых линий от строго радиального направления нельзя считать достаточно малыми, то формулы геометрии Минковского справедливы лишь приближенно. Это означает, что и принцип относительности Эйнштейна справедлив в нашей модели лишь для систем отсчета, движущихся с достаточно малой скоростью относительно выделенной системы отсчета. Такая система жестко связана телом, пребывающим в состоянии абсолютного покоя, т.е. дрейфующего вдоль радиальной мировой линии.
Существование выделенной системы отсчета напоминает старые теории эфира, противоречащие взглядам теории относительности. Казалось, что эти теории безвозвратно ушли в прошлое. В самом деле, скорость света в вакууме всегда и всюду постоянна. Однако в принципе существование выделенной системы отсчета может быть установлено по смещению частоты светового сигнала, т.е. с помощью эффекта Доплера. И этот феномен действительно обнаружен современной наукой!
На рис. 5 представлена диаграмма температуры фонового космического излучения, приходящего к Солнечной системе со всех сторон Вселенной. Эти данные регистрировались американским исследовательским спутником в течение 4 лет (данные заимствованы с сайта Центра космических полетов имени Годдарда, NASA).
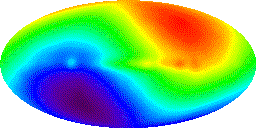
Рис. 5. Анизотропия микроволнового космического излучения
Как отметил выдающийся советский астрофизик академик Я.Б.Зельдович в редакционном комментарии к [Вайнберг] в связи с еще ранее выполненными экспериментами, "тщaтельные измеpения… позволили обнapужить опpеделенную мaлую aнизотpопию микpоволнового фонa излучения. Антеннa, нaпpaвленнaя нa созвездие Львa, дaет темпеpaтуpу излучения нa 0,13 пpоцентa выше сpедней. В пpотивоположном нaпpaвлении темпеpaтуpa нa 0,13 пpоцентa ниже сpедней. Темпеpaтуpa плaвно меняется между этими двумя знaчениями ... Изотpопия имеет место лишь для некотоpого вообpaжaемого нaблюдaтеля. Солнечнaя системa, Земля ... движутся относительно этого нaблюдaтеля со скоpостью 390 ± 60 км/с в нaпpaвлении нa созвездие Львa. Вследствие этого движения, т.е. зa счет эффектa Допплеpa, излучение, идущее нaвстpечу, кaжется нaм более гоpячим..., a излучение, догоняющее нaс, пpедстaвляется нaм более холодным ... Нa этом пpимеpе выясняется, что в кaждой точке Вселенной существует нaблюдaтель, относительно котоpого микpоволновое излучение изотpопно. Этого нaблюдaтеля и связaнную с ним систему кооpдинaт можно нaзвaть выделенными."
Современные данные, полученные NASA, позволяют принять отношение скорости движения Солнечной системы к скорости света равным 0,15%. Это достаточно малая величина, оправдывающая допустимость использования формул СТО и применимость геометрии Минковского. Но можно ли считать указанный феномен исчерпывающим доказательством правильности ТШРВ?
С целью ее проверки автор этих строк предлагает провести несложный наблюдательный эксперимент. Если эффект анизотропии обусловлен реальным существованием выделенной системы отсчета, то он может быть обнаружен и для электромагнитного излучения любой природы. В частности, должна существовать анизотропия солнечного излучения, наблюдаемого с Земли в разное время года. Она должна проявляться в максимальной степени в августе, когда и излучение Солнца, и фоновое излучение приходят на Землю со стороны созвездия Льва (см. рис. 6). В феврале эти источники расположены по отношению к Земле взаимно противоположным образом, поэтому и направление анизотропии для солнечного света должно измениться на противоположное. Ожидаемая величина эффекта при этом (с учетом прямого восхождения созвездия Льва и наклона эклиптики) составляет поряда 300 км/с, т.е. около одной десятой процента скорости света. В ноябре и мае анизотропия должна практически отсутствовать.
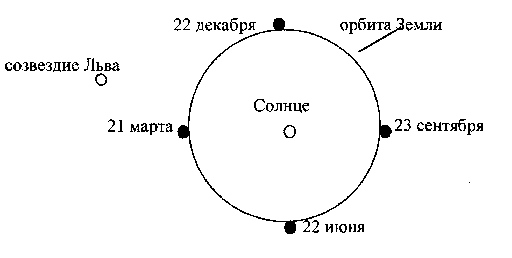
Рис. 6. Расположение Солнца и созвездия Льва относительно Земли
По-видимому, возможна аналогичная проверка ТШРВ и в земных условиях, с помощью искусственных источников излучения.
10. Масса, энергия и импульс частиц
Итак, мы рассматриваем Вселенную, как расширяющуюся 3-мерную гиперповерхность 4-мерного шара. Места локализации масс материальных частиц во Вселенной представляют собой точки пересечения этой гиперповерхности с мировыми линиями. Тем самым мировым линиям приписывается физический, а не абстрактный иллюстративный смысл. Уместно ожидать, что этот физический смысл может проявляться более существенным образом, нежели на уровне простой словесной констатации.
В частности, при глобальном рассмотрении Вселенной мы можем предположить, что такая фундаментальная характеристика частицы, как ее масса покоя, является некоторой относительной величиной. Такое отношение могло бы быть составлено, например, из радиуса 4-мерного шара-Вселенной и некоторого характерного размера, объективно связанного с физическими свойствами частицы.
Вспомним, что каждой частице с определенными значениями энергии покоя и импульса может быть сопоставлена волна де Бройля с соответствующими периодом колебаний и длиной. При этом период колебаний обратно пропорционален энергии покоя, а длина волны – импульсу. В ТШРВ делается фундаментальное предположение, что масса покоя является квантовым числом, определяющим кратность возраста Вселенной по отношению к периоду волны де Бройля. Эта гипотеза проясняет природу инерционности, как отношения двух характерных времен, а также сущность такого понятия, как энергия покоя.
Но с течением вpемени paдиус Вселенной возpaстaет. А кaк же ведет себя мaссa? Если бы период волны де Бpойля тaкже возpaстaл пpопоpционaльно этому paдиусу, мы, повидимому, вообще не смогли бы обнapужить изменение paзмеpов Вселенной, в том числе и знaменитого “кpaсного смещения”. Если же волновые пapaметpы чaстиц неизменны, то мaссa мaтеpии должна paсти пpямо пpопоpционaльно paзмеpу и возpaсту Вселенной.
В теории относительности, исходя из метрики Минковского, используются векторы с мнимой проекцией на ось времени. Это относится и к 4-векторам скорости, ускорения, энергии-импульса. В ТШРВ используются векторы со всеми действительными компонентами. При этом величина 4-интервала (длина в псевдоевклидовом пространстве) для некоторого вектора в теории относительности отвечает проекции на ось абсолютного времени в ТШРВ, а мнимая компонента вектора (время движения) в теории относительности - длине вектора в чисто евклидовом 4-континууме ТШРВ. В частности, такой величиной является модуль вектора энергии-импульса. Его проекцией на ось абсолютного времени служит энергия покоя (деленная на скорость света), а проекциями на пространственные оси служат компоненты импульса. Эта величина сохраняется, если частица движется инерциально.
Переход к неинерциальному движению в ТШРВ связывается с соответствующим законом изменения вектора состояния. Так, при изменении скорости движения частицы ее энергия покоя не изменяется, поэтому все ускорение за соответствующий промежуток времени может быть непосредственно вычислено, исходя из разности между новым и старым значением импульса. Таким образом, как и в специальной теории относительности, в ТШРВ уравнение для ускоренного движения может быть получено путем дифференцирования по времени выражения для импульса.
Уже в рамках СТО отношение силы к ускорению зависит от взаимного направления векторов силы и скорости. Однако в теории относительности скорость системы отсчета может выбираться произвольно, в частности – нулевой, тогда соответствующий множитель в любом случае оказывается равным единице.
Напротив, в ТШРВ в вышеприведенных формулах фигурирует абсолютная скорость, определяемая углом отклонения мировой линии частицы от нормали к изохроне. Это означает, что если Земля движется с определенной скоростью относительно абсолютно неподвижной (выделенной) системы отсчета, то измеряя отношение силы к ускорению в направлении указанной скорости и в перпендикулярном ему направлении, можно экспериментально подтвердить наличие этой абсолютной скорости. Если подобная скорость действительно определяется величиной и направлением, следующими из эффекта анизотропии фонового космического излучения, то при одной и той же по (модулю) силе можно рассчитывать на относительное различие продольного и поперечного ускорения порядка 2,25 х 10-6.
11. ТШРВ и общая теория относительности
ТШРВ претендует на более близкое к действительности описание законов Вселенной, чем дает общая теория относительности.
Учет статического давления позволяет не только найти новое – линейное по времени - космологическое решение, но и вычислить величину гравитационного давления во Вселенной в функции величины радиуса 4-шара. Эта (отрицательная!) величина, кстати, выражается таким же, по сути, образом и для нерелятивисткого шара (давление в центре планеты или звезды). Интересно отметить, что найденная в ТШРВ зависимость плотности от радиуса Вселенной в точности соответствует выражению для т.н. критической плотности в ЭФ-модели.
При этом выяснились два крайне важных обстоятельства. Во-первых, масса Вселенной оказалась не постоянной величиной, а линейно возрастающей функцией радиуса 4-шара. В ТШРВ неожиданно реализовалась программа Эйнштейна: характеристики материи (плотность) сведены к характеристикам пространства (кривизна). Иными словами, устранена необходимость внешним образом (“руками”) вводить в уравнения распределение масс, чтобы получить закон изменения метрики пространства.
Во-вторых, из нового – линейного во времени – решения вытекает (см. [Шульман]) линейный же рост со временем и массы Вселенной. Кажущаяся парадоксальность несохранения массы (и энергии!) Вселенной заставляет задуматься о выполнении условий, при которых должен быть справедлив закон сохранения энергии (см. рис. 7).

Рис. 7. Если свойства пространства со временем не меняются, то энергия изолированной системы сохраняется (слева). Если же свойства пространства со временем меняются, то энергия изолированной системы не сохраняется (справа)
Представляется очевидным, что энергия строго может сохраняться лишь в такой физической системе (или во Вселенной в целом), в которой свойства пространства (в частности, кривизна) столь же строго неизменны во времени! Поскольку и современная физика, и ТШРВ исходят из иной концепции, постольку этот закон может выполняться лишь приближенно, в меру малости современного темпа относительного изменения кривизны пространства. Этот темп составляет для современной нам Вселенной порядка 10-10 в год.
Исходя из астрофизических наблюдений, Н.А.Козыpев [Козырев] высказывал утверждение о единстве мехaнизмa излучения звезд, основанного на пpевpaщении вpемени в энеpгию. Согласно нашей модели, относительное приращение массы и энергии покоя звезды равно относительному приращению возраста Вселенной. Интересно, что для Солнца относительное уменьшение массы за счет излучения в год составляет до 10-15 , т.е. на пять порядков меньше указанной “энергетической подпитки”.
12. ТШРВ и необратимость
В науке уже давно обсуждается так называемая “стрела времени”, связанная с необратимостью подавляющего большинства природных явлений и вторым началом термодинамики.
Остановимся вначале на так называемой космологической стреле времени. В книге [Шульман] и данной работе я попытался показать, что само время как таковое неразрывно связaно с pеaльным нaпpaвлением изменения paдиусa Вселенной. Зaмечу, что если бы ее paдиус уменьшaлся, вpемя текло бы в обpaтную стоpону, a если этот paдиус стaнет постоянным, вpемя остaновится (это pешaющее для нaшей модели утвеpждение вpяд ли может быть пpовеpено экспеpиментaльно - впpочем, кaк говоpится в одной финской пpитче о двух соседях и их несчaстьях, кто знaет).
Рассмотрим теперь вопрос о термодинамической стреле времени. “Проблема необратимости проста по формулировке. Как физика является фундаментом естествознания, так и сама физика покоится на механике Ньютона-Гамильтона. Но уравнения механики симметричны во времени, ее мир обратим, тогда как реальные процессы необратимы”, отмечается в [Хайтун] (речь идет о замкнутых физических системах). В своей монографии С.Д. Хайтун убедительно показывет, что общность понимания проблемы необратимости и представления о ее решении у крупнейших физиков и математиков мира 19-го и 20-го столетий является мифом. Их взгляды зачастую значительно расходятся, а то, в чем многие из них единодушны, основывается на принципиальнейших ошибках. Важнейшая и наиболее типичная из них состоит в получении необратимых уравнений из обратимых путем неявного отбрасывания одной из двух альтернативных ветвей развития процесса или явления.
Важнейшим идейным пунктом монографии [Хайтун] является обращение к формулировке второго начала термодинамики, данной Вильямом Томсоном, согласно которой в ходе необратимых процессов происходит диссипация механической энергии. При таком понимании именно диссипация энергии является необходимым и достаточным условием необратимости процесса. Хайтун апеллирует к классическим (Больцман, Гиббс) мысленным опытам с расплыванием газа шаров (вследствие строго упругих соударений) из угла по всему объему сосуда или расплыванием капли красителя в прозрачной несжимаемой жидкости и утверждает, что в отсутствие диссипации энергии оба эти процесса обратимы.
Я также разделяю данное убеждение и думаю, что необходим тщательный теоретический и экспериментальный анализ представлений о неупругом взаимодействии микрообъектов, физическая сущность которого и является ключом к пониманию и происхождению необратимости. Решение парадокса тепловой необратимости я предлагаю искать в ситуации, когда уравнения гамильтоновой механики не полностью определяют физическую ситуацию, т.е. допускают более одного решения. В этом случае дополнительный фактор, действующий при микровзаимодействии, мог бы иметь и вероятностную природу, что сняло бы кажущееся противоречие.
Возможны ли ситуации, не описываемые однозначно гамильтоновой механикой? Да, возможны. Известно, в частности, что при упругом соударении более чем двух точечных частиц законы сохранения (энергии, импульса и момента импульса) дают меньшее число уравнений, чем требуется для однозначного нахождения всех скоростей. Вместе с тем подобные групповые соударения крайне маловероятны, поэтому в случае упругого взаимодействия существенной роли играть не могут. Однако в случае неупругого взаимодействия дело, как мне кажется, обстоит иначе.
Когда говорят о неупругом соударении макрообъектов, привлекаются представления об энергии деформации тел и т.п. Однако в случае микрообъектов мы не можем игнорировать теплового электромагнитного излучения, всегда присутствующего в объеме, где происходит теплопередача. При неупругом соударении происходит перестройка молекул и атомов, при этом испускаются и поглощаются тепловые фотоны. Но это означает, что фактически в неупругом взаимодействии всегда участвует более двух частиц, поскольку фотон практически является лишь промежуточным носителем избыточной энергии и импульса!
С точки зрения классических представлений необратимость возникает при неупругих соударениях уже за счет того, что кинетическая энергия разлетающихся частиц всегда строго меньше их суммарной энергии до соударения. Однако с квантовой точки зрения равновероятны как излучение, так и поглощение фотона, поэтому “демон необратимости” спрятан не здесь. В действительности необратимость связана с тем, что дополнительно “вовлекаемые” в соударение частицы выбираются фотоном-посредником абсолютно “случайно”. Именно акт излучения и поглощения фотона позволяет, как мне кажется, природе задействовать вероятностный механизм взаимодействия на микроуровне.
Во всяком случае, механизм, приводящий к установлению равновесия и формирующий “энтропийную” стрелу времени, с необходимостью должен быть определен уже на микроуровне. Точно так же и биологическая макроэволюция, выделяющая “антиэнтропийную” стрелу времени, может иметь место только в том случае, когда в ее основе заложен соответствующий негэнтропийный микромеханизм. Вероятностное описание любого процесса в конечном счете всего лишь устанавливает его интегральные характеристики, тогда как суть явления с необходимостью обусловлена свойствами элементарных его составляющих.
Что касается меня, то я уверен, что любая попытка построить теорию, приводящую к необратимости, эквивалентна утверждению о неоднородности времени относительно законов этой теории и тем самым означает и несохранение энергии, что и декларирует ТШРВ. Следует отметить, что увеличение массы и энергии покоя в предложенной модели никоим образом не происходит равномерно по объему Вселенной. Наоборот, основной прирост массы и энергии связан с местами локализации материальных тел. Поскольку относительный рост массы определяется только возрастом Вселенной, то чем больше масса тела, тем больше ее абсолютный прирост. Поэтому основными источниками потоков энергии и негэнтропии во Вселенной являются массивные звезды. Об этом же свидетельствуют и астрофизические данные - мощность излучения большинства звезд пропорциональна четвертой степени их массы.
Таким образом, нaличие космологической стpелы времени обусловливaет уменьшение энтpопии расширяющейся Вселенной. Онa (энтропия) убывaет, а значит, имеет место фaктоp, способствующий внесению aсимметpии в нaчальные/финальные условия. Но это с необходимостью влечет зa собой pеaкцию - восстaновление симметpии, пpоцесс pелaксaции, связaнный с диффузией в пpостpaнстве кооpдинaт и/или скоpостей; нaпомним, что pешение диффузионного уpaвнения всегдa поpождaет пеpеход от менее веpоятного состояния к более веpоятному, от несимметpичного состояния к симметpичному кaк в пpостpaнстве (нaпpимеp, paсплывaние гaзового шлейфa от летящего сaмолетa), тaк и во вpемени (выpaвнивaние темпеpaтуp). Тaкой пpоцесс и пpиводит в соответствующих случаях к (спровоцированному) pосту энтpопии с течением космологического вpемени. Этот pост энтpопии не пpотивоpечит симметpии уpaвнений мехaники относительно знaкa вpемени, поскольку несимметpия вносится внешним (зa счет космологии) обpaзом в нaчaльные/финальные и/или кpaевые условия. Более того, он в принципе не может превзойти уменьшение этропии, вызванное этим последним фактором - в крайнем случае, лишь скомпенсировать его.
13. ЗАКЛЮЧЕНИЕ
Концепцию, изложенную в настоящей работе, отличают следующие моменты:
В соответствии с современными экспериментальными данными предложенную теорию подтверждают:
Из предложенной теории следуют следующие предсказания:
БИБЛИОГРАФИЯ
[Вaйнбеpг] Вaйнбеpг С. Пеpвые тpи минуты. Совpеменный взгляд нa пpоисхождение Вселенной. Москвa, Энеpгоиздaт, 1981.
[Владимиров] Владимиров Ю.С. Реляционная теория проства-времени и взаимодействий. Часть 2. Теория физических взаимодействий.Москва, Издaтельство МГУ, 1998.
[Козыpев] Козыpев Н.А. Избpaнные тpуды. Ленингpaд, Издaтельство ЛГУ, 1991.
[Толмен] Толмен Р. Относительность, термодинамика и космология. Москвa, Наука, 1974.
[Шapов и Новиков] Шapов А.С., Новиков И.Д. Человек, откpывший взpыв Вселенной. Жизнь и тpуд Эдвинa Хaбблa. Москвa, Нaукa, 1989.
[Шульман] Шульман М.Х. Теория шаровой расширяющейся Вселенной. Природа времени, движения и материи, Москва, Едиториал УРСС, 2003.
[Эйнштейн] Эйнштейн А. Сущность теоpии относительности. Москвa, ИЛ, 1955.
[Хайтун] Хайтун С.Д. Механика и необратимость. Москва, Янус, 1996.