 . (1)
. (1)глава 1. физика
БИНАРНАЯ ГЕОМЕТРОФИЗИКА
§1. Введение
В основе фундаментальной теоретической физики лежит теория пространства-времени. Все главные достижения физики ХХ века: специальная теория относительности, общая теория относительности и квантовая теория — связаны с изменением представлений о свойствах пространства-времени. Сейчас среди физиков-теоретиков все более крепнет убеждение, что геометрия реального пространства-времени есть физика, и основания физики должны описываться геометрией обобщенного пространства-времени. Дальнейший прогресс в фундаментальной теоретической физике следует ожидать на пути очередного пересмотра представлений о сущности физического пространства-времени.
Современная физика строится в рамках модели готового (плоского или искривленного) пространства-времени, имеющего характер вместилища всего сущего. Эти представления бытуют со времен Декарта и Ньютона. По убеждению автора, дальнейшее развитие физики и геометрии должно быть связано с переходом к реляционной трактовке пространства-времени, т.е. к его пониманию как некой системы отношений между материальными образованиями. В таком понимании без материи нет и пространства-времени. Этот подход обычно связывается с именами Г.Лейбница и Э.Маха (Мах, 1909). Он альтернативен субстанциальным представлениям о природе пространства и времени, которых придерживались В.Клиффорд и Дж.Уилер.
Подходящей основой для развития реляционной концепции пространства-времени является теория бинарных физических структур, построенная Ю.И.Кулаковым для переформулировки ряда законов общей физики (Кулаков, 1968). В этой теории постулируется существование двух множеств элементов и отношений между ними, удовлетворяющих некоторым алгебраическим условиям. В теории физических структур Кулакова отношения — это вещественные числа, сопоставляемые элементам из одного или из двух разных множеств.
Нам представляется, что новая физическая картина мира должна опираться на систему элементарных понятий, заимствованных из физики микромира, из которых бы выводились понятия как классического пространства-времени, так и теории известных видов фундаментальных физических взаимодействий. Для построения такой теории, названной автором бинарной геометрофизикой (БГФ) (Владимиров, 1992), использована комплексифицированная теория бинарных физических структур симметричных рангов (
r,r). Только в этом случае имеется возможность отразить свойства физики микромира. Упрощенные математические модели такой теории конкретного ранга названы бинарными системами комплексных отношений (БСКО).В рамках БСКО первого невырожденного ранга (3,3) можно построить прообраз 4-мерного классического пространства-времени Минковского, 3-мерную гиперболическую геометрию (Лобачевского), интерпретируемую в рамках БГФ как импульсное пространство выделенного класса свободных частиц. Предлагается их трактовать как идеализированные (т.е. невзаимодействующие) массивные лептоны (первого поколения).
В настоящей работе показано, что для получения реалистической теории взаимодействующих частиц необходимо опереться на БСКО более высоких рангов — на бинарное многомерие, являющееся прообразом общеизвестных (унарных) многомерных теорий Калуцы — Клейна. Идеи многомерия составляют второй блок исходных принципов, положенных в основу БГФ.
В рамках БГФ теория физических взаимодействий должна строиться в духе теории прямого межчастичного взаимодействия (ТПМЧВ) типа Фоккера — Фейнмана с той разницей, что как прообраз действия, так и пространственно-временные отношения описываются однотипными понятиями из отношений между частицами. Идеи ТПМЧВ составляют третий блок принципов БГФ.
В данной работе продемонстрирован переход от БСКО ранга (4,4) и соответствующей ей плоской 3-точечной геометрии к многомерной искривленной 2-точечной геометрии, используемой в теориях Калуцы — Клейна. Искривленное пространство-время общей теории относительности предлагается понимать как 4-мерное пространственно-временное сечение многомерной 2-точечной геометрии, возникающей из БСКО ранга (4,4) путем редукции ее к 4-мерной теории.

Рис.1. Бинарная система отношений ранга (
r, s)
§2. Основные понятия бинарной геометрофизики
Теория бинарных систем отношений (бинарных структур) изложена в ряде наших работ (Кулаков и др., 1991; Vladimirov, 1995). Напомним самые необходимые понятия. В теории бинарных систем отношений исходным является закон
F для отношений uia между элементами двух множеств i О M и aО N. В первом множестве M элементы нумеруются латинскими индексами, а во втором — греческими (рис.1). Ранг (4,4) означает, что закон записывается для 4 произвольных элементов множества M и для 4 произвольных элементов множества N. Согласно общей теории закон БСКО ранга (4,4) для элементов i, k, j, s; a, b, g, d записывается в виде  . (1)
. (1)
Легко показать, что этот закон тождественно выполняется, если каждый элемент характеризуется тремя комплексными числами (
i ® i1, i2, i3; a® a1, a2, a3), и парное отношение представляется через них в видеuia = i1a1 + i2a2 + i3a3. (2)
Фактически это скалярное произведение двух векторов в
3-мерном комплексном пространстве.Теорию БСКО ранга (
4,4) можно понимать как своеобразное многомерное обобщение теории БСКО ранга (3,3), ответственной за наблюдаемое классическое 4-мерие (Владимиров, 1988). Напомним, что закон БСКО ранга (3,3) записывается аналогично (1), но для двух троек разноименных элементов 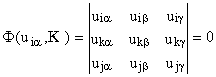 , (3)
, (3)
когда элементы характеризуются лишь двумя комплексными параметрами, а парное отношение имеет вид
uia=i1a1 +i2a2. (4)
В такой теории ключевой характер имеет так называемое фундаментальное
2ґ 2-отношение: 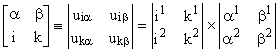 , (5)
, (5)
сопоставляемое двум парам разноименных элементов. Линейные преобразования элементов
![]()
с комплексными коэффициентами ![]() , оставляющие инвариантными отдельные определители справа в (5), образуют группу
, оставляющие инвариантными отдельные определители справа в (5), образуют группу
![]() = hmnpmpn, (7)
= hmnpmpn, (7)
где
hmn — метрический тензор 4-мерного пространства-времени Минковского; pm — компоненты 4-вектора, образованного параметрами двух пар элементов: i, k, a, b. Если элементы i, a и k, b описываются комплексно сопряженными параметрами, то вектор pm вещественен.Аналогичные рассуждения для БСКО ранга (
4,4) выделяют группу преобразований SL(3,C). Из параметров элементов можно построить вещественный 9-мерный вектор. Выделение подгруппы преобразований SL(2,C) соответствует редукции теории БСКО ранга (4,4) к теории в рамках БСКО ранга (3,3), аналогичной редукции многомерных моделей типа теории Калуцы — Клейна к 4-мерной ОТО с дополнительными полями геометрического происхождения. Как известно, они описываются дополнительными компонентами многомерного метрического тензора G5m, G6m и т.д. В данном случае следует поступать аналогично: из параметров с индексами 1 и 2 строятся компоненты 4-мерных векторов pm, а с помощью дополнительных параметров определяются заряды частиц (Vladimirov, 1995; Владимиров, 1992).В бинарной геометрофизике полагается, что в рамках БСКО ранга (
3,3) описываются идеализированные (невзаимодействующие) лептоны: двумя парами элементов из разных множеств описываются массивные лептоны (электроны и позитроны), а одной парой разноименных элементов описываются нейтрино. Реалистические, т.е. взаимодействующие электрослабым образом лептоны описываются такими же числами элементов, однако из редуцированной теории БСКО ранга (4,4) (Vladimirov, 1995).§3. Бинарные системы комплексных отношений и унарные геометрии с симметриями
Опыт работы в рамках эйнштейновской ОТО, многомерных теорий Калуцы — Клейна и квантовой теории показывает, что каждая из них содержит важную составную часть, описывающую переход от первичных понятий к физически наблюдаемым или интерпретируемым величинам. В ОТО это методы описания систем отсчета, в теории Калуцы — Клейна это методы редукции многомерных соотношений и величин к
4-мерным понятиям, в квантовой теории это переход к эрмитовым операторам и их собственным значениям. Аналогичный прием имеется и в бинарной геометрофизике. Он состоит в переходе от БСКО к унарным системам вещественных отношений (УСВО), в рамках которых понятия имеют знакомый геометрический и физический смысл.Это осуществляется склейкой пар или большего числа элементов из двух разных множеств БСКО в некое новое образование, играющее роль элемента унарной системы вещественных отношений (рис.2). Через парные отношения исходной БСКО строятся отношения УСВО. Как правило, склеиваются элементы двух множеств с комплексно сопряженными параметрами. Общая теория УСВО под названием теории физических структур на одном множестве элементов была ранее построена в работах Ю.И.Кулакова (1968), Г.Г.Михайличенко (1972), В.Х.Льва (1988). Было показано, что такие структуры соответствуют известным типам геометрий с группами симметрий. Для них пишутся законы некоторого ранга типа приведенных в (1) и (2) законов БСКО. Так, оказывается, геометрия
4-мерного пространства-времени Минковского описывается УСВО ранга 6. Ее закон записывается в виде равенства нулю определителя Кэли — Менгера на 6 точках: 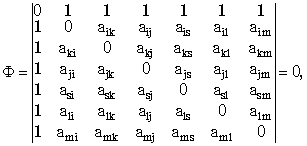 (8)
(8)
где парные отношения представляются в виде
![]() . (9)
. (9)
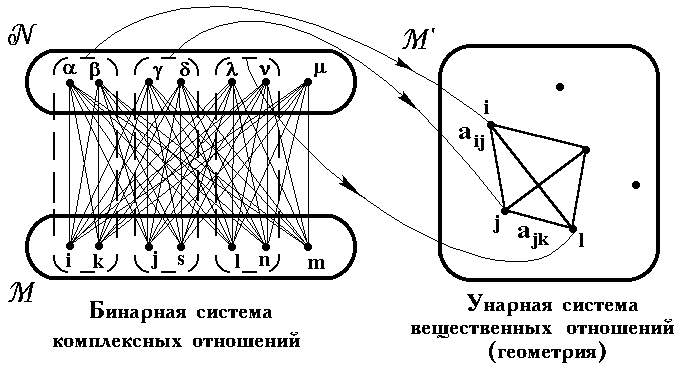
Рис.2. Переход от БСКО к УСВО (геометрии)
Здесь ![]() и
и ![]() — координаты точек-событий в
— координаты точек-событий в
Оказывается, к
4-мерному пространству-времени Минковского можно перейти от БСКО ранга (3,3). Кроме того, получается 3-мерная геометрия Лобачевского (Владимиров, 1993), которая в бинарной геометрофизике интерпретируется как импульсное пространство массивных лептонов.По образу и подобию теории БСКО ранга (
3,3) можно осуществлять переход к УСВО в рамках БСКО ранга (4,4) и более высоких рангов. При этом оказывается, что в итоге получаются геометрические конструкции не только более высокой размерности (в некотором обобщенном смысле), но и с другим мероопределением. Общепринятые парные (квадратичные) метрические отношения оказываются присущими лишь случаю БСКО ранга (3,3). В рамках БСКО ранга (4,4) получаются трехточечные геометрии (когда число, т.е. метрика, задается для трех точек). В рамках БСКО ранга (5,5) получаются 4-точечные геометрии и т.д. Отметим, что многоточечные геометрии независимо от бинарной геометрофизики рассматривались В.Я.Скоробогатько (Скоробогатько и др., 1975). Для таких многоточечных геометрий можно записать законы в духе теории вещественных физических структур Кулакова. Однако в отличие от общепринятых геометрий с квадратичным мероопределением такие законы записываются не через обычные квадратные, а через кубичные и пространственные определители. Теория таких определителей достаточно хорошо развита (Соколов, 1960), однако в теоретической физике они практически не использовались. В наших работах такие законы записаны и введен своеобразный метрический тензор, обобщающий метрику пространства-времени Минковского (Васильев, Владимиров, 1994).§4. Базовое 4
ґ 4-отношение и усреднение по эталонным элементамДо сих пор рассматривались унарные геометрии с симметриями: пространство-время Минковского, геометрия Лобачевского, многоточечные аналоги этих и других геометрий с группами движений. Оказывается, в рамках бинарной геометрофизики можно получить геометрию искривленного пространства-времени риманова типа. Это осуществляется с помощью ряда довольно естественных принципов.
Принцип 1
. Поскольку риманова геометрия, лежащая в основе ОТО и теорий Калуцы — Клейна, является унарной геометрией с парными вещественными отношениями, а в рамках БСКО ранга (4,4) получаются 3-точечные геометрии, то переход от трехточечной метрики к двухточечной должен осуществляться суммированием трехточечных отношений с участием двух избранных “точек” по всем третьим “точкам”. Символически это можно представить в виде a(1,![]() ) =
) =![]() , (10)
, (10)
где слева стоит парное отношение между избранными “точками”
1 и 1', а справа — сумма тройных отношений по всем третьим точкам, символически обозначенных цифрой 2 (как вторые частицы).Принцип 2. В качестве исходных тройных отношений будем выбирать выражение, во-первых, симметрично построенное из параметров двух четверок элементов, описывающих две массивные частицы (в рамках БСКО ранга (
4,4) это пара лептонов), и, во-вторых, инвариантное относительно характерной для БСКО ранга (4,4) группы преобразований SL(3,C). Таковым является базовое 4ґ 4-отношение, записываемое через окаймленный определитель из парных отношений 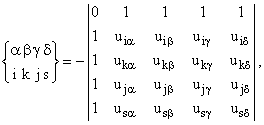 (11)
(11)
где элементы
i, k, a, b соответствуют выделенной частице (1), а элементы j, s, g, d определяют вторую частицу (2). Легко видеть, что это выражение записывается в виде совокупности из 16 фундаментальных 3ґ 3-отношений, инвариантных относительно группы SL(3,C).Принцип 3. Для перехода к классическим понятиям необходимо произвести усреднение по совокупности базисных элементов, составляющих классический макроприбор (классический наблюдатель). Подчеркнем, что до сих пор параметры элементов имели смысл отношений к некоторой тройке эталонных элементов. Это могла быть отдельная частица.
Усреднение по совокупности базисных элементов включает в себя две основные процедуры:
а) Суммирование по третьим элементам базиса, которое интерпретируется в духе принципа Маха, т.е. третьи параметры элементов трактуются как некие эффективные отношения ко всем частицам мира. На практике это означает выделение подгруппы преобразований
SL(2,C), затрагивающей лишь пару параметров с индексами 1 и 2. Третий параметр остается инвариантным. В результате такого выделения базовое 4ґ 4-отношение (11) представляется в виде суммы из 36 лоренц-инвариантных слагаемых вида ![]() . (12)
. (12)
б) Суммирование по всем различным системам отношений, характеризуемым значениями невырожденных параметров (с индексами
1 и 2). Это будет выражаться, в частности, в виде интегрирования по импульсам обмена между взаимодействующими частицами (по импульсам “промежуточных бозонов”).Принцип 4. Для перехода к классическим понятиям следует положить, что как выделенная “частица” так и окружающие ее частицы (2) представляют собой макрообъекты. В частности, это означает усреднение по поляризациям составляющих его частиц. Импульсы частиц определены параметрами с индексами
1 и 2 неоднозначно, с точностью до преобразований на 3-мерной гиперсфере. Усреднение по поляризациям означает интегрирование по этой гиперсфере. В итоге такого усреднения из названных выше 36 лоренц-инвариантных слагаемых базового 4ґ 4-отношения выживают лишь 6 “диагональных” слагаемых, которые составляют комбинацию 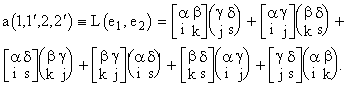 (13)
(13)
Это выражение было использовано в одной из предшествующих работ (Vladimirov, 1995) в качестве алгебраического аналога лагранжиана электрослабых взаимодействий двух массивных лептонов.
Кроме того, переход к макрообъектам означает пренебрежение слагаемыми, содержащими псевдовекторные слагаемые (в стандартной теории означающие взаимодействие через
Z-бозоны). Векторные слагаемые интерпретируются как 4-мерные импульсы частиц (Владимиров, 1988).§5. Основные принципы перехода к многомерной теории Калуцы— Клейна
Принцип 5. Для каждой из частиц две комбинации из дополнительных параметров составляющих их элементов имеют физический смысл
5-й и 6-й компонент многомерного импульса:i3+ k3 є C1L+ C1R ® ![]() ; i3-k3 є C1L- C1R ®
; i3-k3 є C1L- C1R ® ![]() ;
;
j3+ s3 є C2L+ C2R ® ![]() ; j3-s3 є C2L- C2R ®
; j3-s3 є C2L- C2R ® ![]() . (14)
. (14)
Аналогичные выражения имеют место для сопряженных параметров.
Этот принцип фактически означает переход к вырожденной БСКО ранга (
4,4;a) (Владимиров и др., 1992), когда третьи параметры представляются в виде ![]() , (15)
, (15)
где
i0 и a0 — новые параметры, имеющие размерность импульсов. Напомним, что в теории БСКО ранга (4,4;а) парные отношения представляются в видеaia = i1a1 + i2a2 + i0 + a0. (16)
При замене параметров с индексами
3 на параметры с индексами 0 стрелки в (14) превращаются в знаки равенства.Принцип 6. Для взаимодействующих частиц параметры начальных и конечных состояний более не связаны условием комплексного сопряжения. Это условие обобщается на
![]() (17)
(17)
где слева стоит комплексное выражение, построенное по общепринятым правилам для взаимодействующей частицы, а справа ![]() — конечный импульс первой частицы,
— конечный импульс первой частицы,
Принцип 7. Фазы экспоненциальных слагаемых, введенные в (17), представляются через
4-импульсы и координаты классического пространства-времени. Для конечных состояний имеем факторas, bs ~ exp{i
где
s =1, 2;is, ks ~ exp{-if1} = exp
где ![]() и
и ![]() — начальные значения импульса и координат частицы.
— начальные значения импульса и координат частицы.
Легко видеть, что произведение экспоненциальных слагаемых в (17) можно представить в виде
exp![]() (20)
(20)
где положено
![]() . (21)
. (21)
В дальнейшем будем полагать
dS1 малым и разлагать экспоненту в ряд по dS1, оставляя нулевой, первый и второй порядки: ![]() . (22)
. (22)
Величину
dS1 можно представить в виде dS1 =mcds1, где m — масса частицы, ds1 — смещение вдоль ее классической траектории. Тогда парное отношение (10) представляется в виде 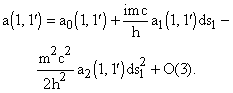 (23)
(23)
Принцип 8. Постулируем, что нулевой и первый порядки разложения в (23) обращаются в нуль:
![]() ; (24)
; (24)
![]() , (25)
, (25)
т.е. парное отношение ![]() в основном приближении пропорционально квадрату
в основном приближении пропорционально квадрату
![]() (26)
(26)
Этот принцип сводит суммарное эффективное парное отношение выделенной частицы, построенное в рамках БСКО ранга (
4,4), к парному отношению теории БСКО ранга (3,3).Принцип 9. Положим, что
ds1 представляет собой смещение частицы вдоль некой дополнительной координаты x4, тогда из суммы и разности (24) и (25) получаем два выражения. Одно из них, помноженное наВыпишем явно условие
7-оптики: ![]() (27)
(27)
где компоненты
7-мерной метрики имеют вид ![]() (28)
(28)
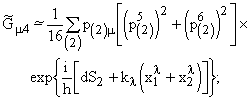 (29)
(29)
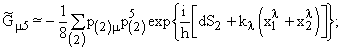 (30)
(30)
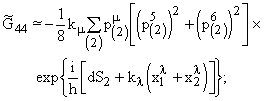 (31)
(31)
 (32)
(32)
 (33)
(33)
![]() , (34)
, (34)
где в знак суммирования включены все суммирования как по частицам, составляющим рассматриваемые объекты, так и по системам отношений макроприбора.
§6. Электромагнитное взаимодействие
Выделим в метрике (27) слагаемые, описывающие электромагнитное взаимодействие:
![]() (35)
(35)
где
A, B =0, 1, 2, 3, 5. Имея в виду, что компонента метрики 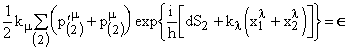 , (36)
, (36)
где ![]() . Это соответствует известному в электродинамике условию Лоренца. Тогда можно записать
. Это соответствует известному в электродинамике условию Лоренца. Тогда можно записать
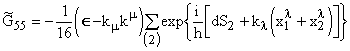 . (37)
. (37)
Из современной формулировки
5-мерной теории Калуцы — Клейна известно (Владимиров, 1987), что для отождествления компонент многомерной метрики с физическими величинами необходимо произвести две процедуры: (1) конформного преобразования исходной метрики и (2) операцию 1+4-расщепления. В качестве конформного фактора выберем величину 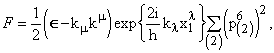 (38)
(38)
так что ![]()
Процедуру
1+4-расщепления следует производить с метрикой GAB. Для этого используем монадный метод в калибровке типа хронометрической в 4-мерной ОТО (Владимиров, 1982). Используя стандартные формулы, находим 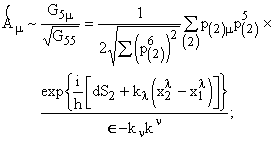 (39)
(39)
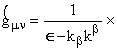 (40)
(40)
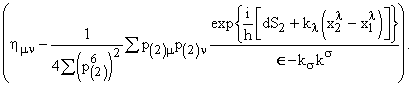
Вспомним, что процедура усреднения по эталонным элементам, образующим классический макроприбор, соответствует использованию совокупности систем отсчета, т.е. в формулах (39) и (40) следует перейти к интегрированию по
d4k. Кроме того, следует учесть, что ![]() (41)
(41)
В нашем случае вместо
d-функции получается сингулярная функция  (42)
(42)
которая известным образом связана с
d-функцией. В этой формуле малая величина e определяет контур интегрирования.§7. Гравитационное взаимодействие
Отдельно рассмотрим слагаемые, описывающие гравитационное взаимодействие. Для этого пренебрежем электромагнитным взаимодействием и запишем
5-мерную метрику, где в качестве пятой координаты выступает x4, ![]() (43)
(43)
Сделаем конформное преобразование с конформным фактором, установленным ранее из вида компоненты ![]()
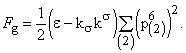 (44)
(44)
Далее произведем
1+4-расщепление 5-мерной метрики по рецептам монадного метода в калибровке типа хронометрической. Поскольку имеется недиагональная компонента метрики G4m, то физически интерпретируемая 4-мерная метрика принимает вид 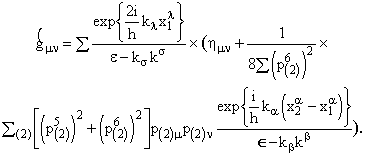 (45)
(45)
Здесь за скобку вынесено выражение, содержащее информацию о положении выделенной частицы (объекта) относительно начала координат эффективной системы отсчета, а в скобках оказались компоненты метрики пространства-времени Минковского и вклады в метрику со стороны всех других частиц мира. Естественно положить, что метрике эйнштейновской ОТО соответствует выражение, стоящее в круглых скобках. Вспоминая, что в знак суммирования входит усреднение по всем эталонным элементам БСКО, составляющим макроприбор, приходим к
4-мерной метрике вида 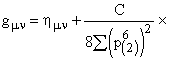
 (46)
(46)
где
C — некоторый размерный коэффициент.Отметим, что это выражение соответствует часто используемому в ОТО представлению римановой метрики через метрику пространства- времени Минковского и малые добавки к ней
gmn = hmn + hmn , (47)
где величины
hmn квадратичны по 4-мерным скоростям источников, т.е. для пылевидной материи пропорциональны компонентам энергии-импульса источников.Заметим также, что в теории прямого межчастичного гравитационного взаимодействия в основном приближении по гравитационной константе также получается эффективная риманова метрика вида (47), где
hmn содержит в себе интегрирование по компонентам тензора энергии-импульса источников (см., например, (владимиров, Турыгин, 1986)).Не представляет труда объединить формулы двух последних разделов, т.е. рассмотреть объединенную
6-мерную теорию грави-электромагнитных взаимодействий. Для этой цели следует использовать процедуру 1+1+4-расщепления в рамках диадного метода в калибровке типа дважды примененной хронометрической (владимиров, 1982). В этом случае в компоненты искривленной 4-мерной метрики будут давать вклады также электромагнитные слагаемые.Подводя итоги, сделаем ряд выводов.
1. Предложенную теорию можно трактовать как обобщение и развитие концепции дальнодействия в физике, в частности, теории прямого межчастичного взаимодействия Фоккера — Фейнмана. Однако в данном подходе идея дальнодействия распространена и на понятия пространства-времени. Заметим, что ранее в исследованиях такого рода пространство-время полагалось априори заданным.
2. В данном подходе проливается свет на суть дополнительных размерностей в многомерных теориях типа Калуцы — Клейна. Оказывается, они обусловлены дополнительными параметрами бинарных систем комплексных отношений рангов, больших (
3,3).3. В изложенной теории нашла свое развитие идея, содержащаяся в
5-оптике Румера, где в качестве пятой координаты предлагалось взять классическое действие. (Заметим, что на квадрат интервала 4-мерного риманова пространства-времени можно смотреть как на условие 5-оптики.) Однако тогда оказывается, что 5-оптика Румера, строго говоря, не предназначена для описания электромагнитного взаимодействия. Для этой цели необходима еще одна размерность. С другой стороны, в общепринятой теории Калуцы — Клейна до сих пор не рассматривалась координата x4, и рассуждения начинались с искривленных компонент Gmn, фактически уже полученных с ее помощью.4. В предложенной теории решается загадка, долгое время мешавшая восприятию
5-мерия, о сути компоненты G55. Обсуждались различные гипотезы описания с ее помощью дополнительного скалярного поля геометрического происхождения, изменения физических констант и т.д. С точки зрения изложенного здесь подхода компонента G55 играет ключевую роль во всей физике, — ею определяются знаменатели сингулярных функций, входящих в определение промежуточных бозонов переносчиков взаимодействий.5. В данном подходе явно проявились идеи, обычно связываемые с принципом Маха, понимаемом в широком смысле, т.е. как влияние глобальных факторов мира на локальные закономерности и понятия в физике. Это проявляется во многих моментах изложенного подхода: и в трактовке смысла дополнительных параметров, и в определении компонент римановой метрики, и в смысле фактора
О , и в других понятиях. Не случайно Эйнштейн возвел соображения Маха в ранг принципа в связи с определением метрики искривленного пространства-времени (Эйнштейн, 1965, с.613).6. Существенно подчеркнуть, что в определение метрики (гравитационного взаимодействия) вносит существенный вклад
6-я компонента многомерного импульса p6, определяющая взаимодействие лептонов с Z-бозонами в алгебраической модели электрослабых взаимодействий (Vladimirov, 1995).7. Наконец, следует отметить, что в данной работе рассмотрен переход от бинарной геометрофизики к многомерным геометрическим моделям физических взаимодействий в рамках БСКО ранга (
4,4). Для более высоких рангов, с помощью которых можно описывать барионы, суть рассуждений останется той же, лишь формулы будут иметь более громоздкий вид.Литература
Васильев С.А., Владимиров Ю.С. Кубичный аналог 9-мерного пространства Минковского // В сб. тезисов докладов международной школы-семинара “Многомерная гравитация и космология”. М., 1994. с.7.
Владимиров Ю.С. Системы отсчета в теории гравитации. М., 1982.
Владимиров Ю.С. Размерность физического пространства-времени и объединение взаимодействий. М., 1987.
Владимиров Ю.С. Биспиноры и физическая структура ранга (3,3) // Вычислительные системы. 1988. №125. c.42
Владимиров Ю.С. Фундаментальные взаимодействия в бинарной геометрофизике // В сб.: Гравитация и электромагнетизм. Вып.5. Минск, 1992. с.63
-70.Владимиров Ю.С. Бинарные структуры и неевклидовы геометрии // В сб.: Неевклидовы пространства и новые проблемы физики. Сб. статей, посвященных 200-летию Н.И.Лобачевского. М., 1993. с.45
-48.Владимиров Ю.С., Турыгин А.Ю. Теория прямого межчастичного взаимодействия. М., 1986. 134 с.
Кулаков Ю.И. Элементы теории физических структур. (Дополнение Г.Г.Михайличенко). Новосибирск, 1968.
Кулаков Ю.И., Владимиров Ю.С., Карнаухов А.В. Введение в теорию физических структур и бинарную геометрофизику. М., 1991.
Лев В.Х. Трехмерные геометрии в теории физических структур // Вычислительные системы. 1988. №125. c.90
-103.Мах Э. Познание и заблуждение. М., 1909.
Михайличенко Г.Г. Решение функциональных уравнений в теории физических структур // Доклады АН СССР. 1972. Т.206, №5. с.1056
-1058.Румер Ю.Б. Исследования по 5-оптике. М., 1956.
Скоробогатько В.Я., Фешин Г.Н., Пелых В.А. В сб. Математические методы и физико-механические поля. вып.1. Киев, 1975. с.5
-10.Соколов Н.П. Пространственные матрицы и их приложения. М., 19
60.Эйнштейн А. Принципы общей теории относительности // Собрание научных трудов. Т.1. М., 1965.
Vladimirov Yu.S. Binary geometrophysics: space-time, gravitation // Gravitation and Cosmology. 1995. №3. p.184
-190.