© А.Заславский
СОБСТВЕННЫЕ МИРЫ ДИНАМИЧЕСКИХ СИСТЕМ
А. Заславский
ВВЕДЕНИЕ
Мы владеем понятием “система”.
Мы можем рассуждать о системе, отвлекаясь от специфического (семантического) значения её состояний и элементов (Общая система [ 1 ] ).
Мы понимаем, что окружающий нас мир (включая нас самих) также является системой, которую можно рассматривать отвлеченно, как общую динамическую систему (т.е. абстрактную систему с линейно упорядоченным множеством состояний).
Обладая некоторым запасом воображения можно представить себе внешнего наблюдателя (в традициях классической науки – демона), для которого система “наш мир” представляется упорядоченной последовательностью абстрактных событий (состояний, отнесенных к моментам времени демона), о которых можно сказать лишь одно, что они различимы.
При этом мы знаем, что в системе “наш мир”, рассматриваемой с точки зрения её внутреннего наблюдателя (т.е. нас) действуют в нашем времени известные законы движения и взаимодействия подсистем (физических тел).
А теперь представим себя в качестве внешнего наблюдателя некоторой системы, не имеющей прямого отношения к окружающему пространству. Примерами такой системы могут служить конечный или бесконечный автомат, электрическая цепь и т.п. В этом случае наблюдаемая система проявляет себя как временной ряд, не связанный геометрическими отношениями с пространственными объектами нашего мира.
Если запас нашего воображения ещё не исчерпан, то можно представить существование второго демона, но уже в качестве внутреннего наблюдателя рассматриваемой системы, для которого эта система “изнутри” видится так же, как нам видится наш мир.
В общем случае события динамической системы взаимно однозначно соответствуют некоторым моментам времени внешнего наблюдателя и каждому моменту времени внутреннего наблюдателя.
Иными словами, мы предполагаем существование собственных миров общих динамических систем, отображённых в собственных временах и собственных пространствах.
Однако внешне динамическая система представляется линейно упорядоченной последовательностью абстрактных различимых состояний.
Следовательно, если допустить возможность существования отношений “собственный физический мир” на множестве событий общей динамической системы, то следует признать, что единственной внешней причиной таких отношений является линейная упорядоченность событий.
А это значило бы, что математические (физические) законы собственных миров могут быть выведены как непосредственные следствия этой упорядоченности.
При исследовании данной гипотезы будем предполагать, что внутренний наблюдатель собственного мира общей динамической системы является её подсистемой, организованной как однонаправленный автомат с памятью.
1. ПОСТАНОВКА ЗАДАЧИ (АКСИОМАТИКА)
Общая динамическая система (ДС) в контексте данной работы это отношение линейного порядка (цепь событий) на абстрактном множестве, которое в общей теории систем называют объектом состояний общей системы.
Объект состояний не однороден, он представляет собой совокупность ансамблей событий с разными признаками. Каждый такой ансамбль является объектом состояний соответствующей подсистемы (подмножеством цепи событий). Любой из этих ансамблей может быть объектом состояний подсистемы “внутренний наблюдатель”.
Каждому событию ![]() соответствует его порядковый номер в цепи (момент собственного времени
соответствует его порядковый номер в цепи (момент собственного времени ![]() ) и некоторый признак
) и некоторый признак ![]() =
=![]() - состояние (см. рис.1). В тех случаях, когда нам потребуется указать на принадлежность события
- состояние (см. рис.1). В тех случаях, когда нам потребуется указать на принадлежность события ![]() некоторой
некоторой ![]() - той подсистеме будем использовать обозначение
- той подсистеме будем использовать обозначение ![]() . Комбинация признаков в цепи событий и их отношение к различным объектам мира внешнего наблюдателя определяет специфическую сущность и внешние свойства наблюдаемой им системы. При исследовании собственного мира динамической системы отношение её состояний к объектам мира внешнего наблюдателя игнорируется.
. Комбинация признаков в цепи событий и их отношение к различным объектам мира внешнего наблюдателя определяет специфическую сущность и внешние свойства наблюдаемой им системы. При исследовании собственного мира динамической системы отношение её состояний к объектам мира внешнего наблюдателя игнорируется.

Различие или эквивалентность признаков ![]() и
и ![]() двух любых событий
двух любых событий ![]() и
и ![]() есть объективное свойство системы, не зависящее от наблюдателя. Собственно, признак
есть объективное свойство системы, не зависящее от наблюдателя. Собственно, признак ![]() может интерпретироваться различными наблюдателями по-разному (как, например, значение буквы латинского алфавита, или температура, или частота, или иероглиф, или еще как-то), но то, что
может интерпретироваться различными наблюдателями по-разному (как, например, значение буквы латинского алфавита, или температура, или частота, или иероглиф, или еще как-то), но то, что ![]() и
и ![]() различные (одинаковые) состояния, это есть объективное свойство системы, не зависящее от наблюдателя.
различные (одинаковые) состояния, это есть объективное свойство системы, не зависящее от наблюдателя.
Вследствие изложенного в предыдущем пункте, различные наблюдатели, классифицируя события наблюдаемой ими системы по одинаковым признакам, получат тождественные множества классов состояний. Мощность состояния (количество событий с одним и тем же признаком) есть величина, одинаковая для всех наблюдателей. Именно эту величину, вследствие инвариантности к выбору наблюдателя, будем использовать в качестве меры состояния общей ДС в собственном пространстве. Пусть динамическая система при переходе от события ![]() к событию
к событию ![]() оказывается
оказывается ![]() раз в состоянии
раз в состоянии ![]() . Эту величину, являющуюся разностью мощностей состояния
. Эту величину, являющуюся разностью мощностей состояния ![]() в моменты времени
в моменты времени ![]() и
и ![]() , можно рассматривать как расстояние, которое система преодолевает за время
, можно рассматривать как расстояние, которое система преодолевает за время ![]() .
.
Рассматривая поведение ДС в её собственном мире, будем различать два типа собственных пространственно-временных многообразий - виртуальное и реальное. Первое является отображением собственного мира ДС в абстрактном однородном и изотропном пространстве и времени относительно декартовой системы координат, не связанной с пространственными объектами мира внутреннего наблюдателя. Второе является отображением собственного мира ДС в реальном для внутреннего наблюдателя пространстве и времени относительно системы координат, связанной с одной из её подсистем. В данном случае возможность двоякого представления собственного мира системы обусловлена тем, что величины, которыми измеряется изменение её состояния (см. предыдущий пункт) не зависят от выбора системы координат. Вследствие того, что эти величины могут быть одинаково измерены как внутренним, так и внешним наблюдателем, имеется возможность отображать их в разных пространствах.
Задача состоит в том, чтобы построить адекватные математические модели этих многообразий как следствия линейной упорядоченности цепи событий.
2. ОСНОВНЫЕ ТОЖДЕСТВА ЦЕПИ СОБЫТИЙ.
Цепь событий ДС отобразим на диаграмме Хассе, как показано на рисунке 2.
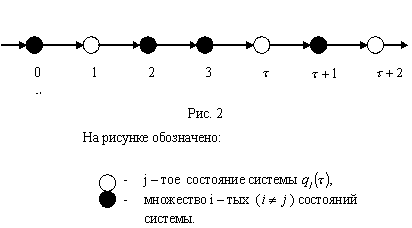
Обозначим ![]() количество
количество ![]() -тых состояний системы на отрезке времени
-тых состояний системы на отрезке времени ![]() . Далее, суммируя все состояния, получим:
. Далее, суммируя все состояния, получим:
![]() (2.1)
(2.1)
Обозначим ![]()
![]() количество переходов из
количество переходов из ![]() -того состояния в
-того состояния в ![]() -тое на отрезке времени
-тое на отрезке времени ![]() . Суммируя переходы из всех
. Суммируя переходы из всех ![]() -тых состояний в некоторое выделенное
-тых состояний в некоторое выделенное ![]() - тое состояние, получим:
- тое состояние, получим:
![]() (2.2)
(2.2)
Отношение количества ![]() -тых состояний системы на отрезке времени
-тых состояний системы на отрезке времени ![]() к количеству всех состояний на этом отрезке времени будем называть вероятностью
к количеству всех состояний на этом отрезке времени будем называть вероятностью ![]() -того состояния
-того состояния
 (2.3)
(2.3)
Суммируя (2.2) по индексу (![]() ), получим:
), получим:
![]() (2.4)
(2.4)
Отношение количества переходов из ![]() -того состояния в
-того состояния в ![]() -тое на отрезке времени
-тое на отрезке времени ![]() к сумме всех переходов на этом отрезке времени будем называть безусловной вероятностью перехода из
к сумме всех переходов на этом отрезке времени будем называть безусловной вероятностью перехода из![]() -того в
-того в ![]() -тое состояние
-тое состояние
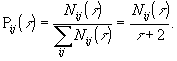 (2.5)
(2.5)
Отношение
![]() (2.6)
(2.6)
будем называть условной вероятностью перехода из ![]() -того в
-того в ![]() -тое состояние (т.е. при условии, что в момент времени
-тое состояние (т.е. при условии, что в момент времени ![]() система находилась в
система находилась в![]() -том состоянии).
-том состоянии).
Суммируя (2.3) по всем индексам ![]() , а также учитывая (2.2), получим систему тождеств цепи событий ДС в виде
, а также учитывая (2.2), получим систему тождеств цепи событий ДС в виде
![]() (2.7)
(2.7)
![]() . (2.8)
. (2.8)
Аналогичными равенствами, известными как уравнения Чепмэна – Колмогорова описывается кинетика марковских цепей.
Преобразуем полученную систему тождеств к дифференциальному виду. Для этого приведём (2.7) к виду
![]()
![]()
![]()
![]() . (2.9)
. (2.9)
Поставим в соответствие элементарному участку цепи длительность ![]()
![]()
![]() . (2.10)
. (2.10)
.Тогда произвольному участку цепи соответствует длительность ![]()
![]()
![]()
![]() . (2.11)
. (2.11)
Среднее приращение вероятности ![]() -того состояния на отрезке времени
-того состояния на отрезке времени ![]() равно
равно

![]()
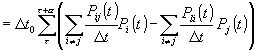 . (2.12)
. (2.12)
В пределе, при ![]() получаем
получаем
![]()
![]() (2.13)
(2.13)
![]()
![]() (2.14)
(2.14)
где ![]()
![]() - плотности вероятностей переходов.
- плотности вероятностей переходов.
3. ОСНОВНЫЕ НЕРАВЕНСТВА ЦЕПИ СОБЫТИЙ.
Так как количество состояний ![]() выражается положительным числом, то
выражается положительным числом, то ![]() .
.
Из этого с очевидностью следует первое неравенство цепи событий ДС:
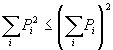 . (3.1)
. (3.1)
Если суммирование осуществляется по всем индексам ![]() , то
, то
![]() (3.2)
(3.2)
Вернемся вновь к модели ДС, изображенной на рис.2. Промежутку времени ![]() соответствует некоторое распределение состояний системы по
соответствует некоторое распределение состояний системы по ![]() признакам. Для наглядности это можно представить себе в виде
признакам. Для наглядности это можно представить себе в виде ![]() шаров разных цветов (количество цветов равно
шаров разных цветов (количество цветов равно ![]() ), уложенных в один ряд. Как известно из теории информации, количество информации
), уложенных в один ряд. Как известно из теории информации, количество информации ![]() , содержащейся в рассматриваемом отрезке цепи событий, равно
, содержащейся в рассматриваемом отрезке цепи событий, равно
![]() (3.3)
(3.3)
где:
 (3.4)
(3.4)
![]() - константа,
- константа, ![]() - количество возможных способов реализации отрезка цепи при заданном ансамбле
- количество возможных способов реализации отрезка цепи при заданном ансамбле ![]() признаков (состояний), каждый из которых включает
признаков (состояний), каждый из которых включает ![]() состояний. В качестве меры неопределённости, снимаемой одним реализованным состоянием ДС, примем среднее количество информации, приходящейся на одно событие
состояний. В качестве меры неопределённости, снимаемой одним реализованным состоянием ДС, примем среднее количество информации, приходящейся на одно событие
![]()
 (3.5)
(3.5)
Эта величина естественным образом ассоциируется с понятием энтропии системы. Заметим, что, применяя формулу Стирлинга к (3.5) в известном приближении ![]() , получаем формулу энтропии системы в обычном виде
, получаем формулу энтропии системы в обычном виде
![]()
![]() (3.6)
(3.6)
Нас интересует приращение энтропии на отрезке времени ![]()
. ![]()
![]()
Подставляя сюда ![]() и
и ![]() из (3.5), найдём
из (3.5), найдём
![]()
 . (3.7)
. (3.7)
На отрезке времени ![]() , вследствие линейной упорядоченности цепи событий, увеличивается на единицу количество событий только одного признака (например
, вследствие линейной упорядоченности цепи событий, увеличивается на единицу количество событий только одного признака (например ![]() ). При этом количество событий с иными признаками
). При этом количество событий с иными признаками ![]() не изменяется. Следовательно, (3.7) можно преобразовать к виду
не изменяется. Следовательно, (3.7) можно преобразовать к виду
![]()
![]() (3.8)
(3.8)
Так как ![]() , второе неравенство цепи состояний получаем в виде:
, второе неравенство цепи состояний получаем в виде:
![]()
![]() . (3.9)
. (3.9)
Иными словами – энтропия общей динамической системы не убывает.
4. CОБСТВЕННОЕ ПРОСТРАНСТВО – ВРЕМЯ ОБЩЕЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ.
В разделе “введение” было высказано предположение о существовании внутреннего наблюдателя общей динамической системы. Без такого предположения не имеет смысла рассуждать о её собственном мире. Совершенно очевидно, что наблюдатель должен являться подсистемой ДС. Это означает, что его собственная цепь событий должна быть подмножеством цепи событий общей системы. Вводя внутреннего наблюдателя, мы предполагаем, что на этом подмножестве задано отношение специального вида – автомат, способный запоминать и анализировать последовательности наблюдаемых событий. Функция наблюдения задаётся упомянутым отношением, как причинно – следственная связь состояний автомата – наблюдателя со всеми событиями наблюдаемой системы. Мы не будем детализировать конструкцию такого автомата. Принципы его построения хорошо изучены теорией автоматов (см. например [2,3,4]). Для нас достаточно осознавать принципиальную возможность его существования. “Если рассматривать человека как односторонний автомат, в котором направление движения ленты совпадает с осью времени, то, в сущности, это эквивалентно утверждению о том, что человек для того, чтобы осуществлять определённые виды деятельности, должен располагать памятью.” (Ф. Джордж [3]).
Какую полезную информацию может извлечь из своих наблюдений наш наблюдатель? Он не может соотнести зафиксированные им события с чем бы то ни было в недоступном его восприятию внешнем мире. Следовательно, наиболее простой (естественный) способ адекватно отображать изменения, происходящие в его собственном мире, состоит в том, чтобы классифицировать события по одинаковым признакам и фиксировать изменения мощностей полученных классов. При этом изменение суммы всех состояний системы воспринимается наблюдателем как изменение времени постольку, поскольку количество моментов собственного времени системы не может быть больше или меньше количества всех её событий. Изменение количества состояний каждого класса в отдельности можно интерпретировать как изменение соответствующей координаты в пространстве состояний системы. Одним из достоинств такого подхода к определению наблюдателя, с нашей точки зрения, является отсутствие необходимости изначально приписывать цепи событий какую-либо алгебраическую структуру. При этом время – пространственные отношения проявляются как следствия статистических закономерностей распределения состояний в цепи событий, а не оказываются заданными изначально. Важно также то, что понятие “расстояние” вводится со ссылкой на способ его измерения путём счёта количеств состояний системы.
Согласно данному выше определению, будем отображать виртуальный мир ДС в евклидовом однородном и изотропном пространстве относительно абстрактной декартовой системы координат. Эта система координат может быть как-то соотнесена с реальными объектами в мире внешнего наблюдателя, однако, безусловно, является абстракцией для внутреннего наблюдателя ДС.
По определению, каждое событие системы характеризуется одним из ![]() признаков (
признаков (![]() может стремиться к бесконечности). Следовательно, множество
может стремиться к бесконечности). Следовательно, множество ![]() событий ДС есть объединение
событий ДС есть объединение ![]() попарно непересекающихся подмножеств (цепей одного признака)
попарно непересекающихся подмножеств (цепей одного признака)
![]() . (4.1)
. (4.1)
Поставим в соответствие цепи ![]() событий системы интервал времени
событий системы интервал времени ![]() , равный
, равный
![]() (4.2)
(4.2)
Каждой цепи событий ![]() - того признака (состояния)
- того признака (состояния) ![]() поставим в соответствие положительное число
поставим в соответствие положительное число ![]() – проекцию приращения вектора состояния
– проекцию приращения вектора состояния ![]() на
на ![]() - тую координатную ось (при единичном базисе)
- тую координатную ось (при единичном базисе)
![]() (4.3)
(4.3)
где: ![]() - константа, устанавливающая соответствие между единицами измерений отрезков времени и пространства состояний.
- константа, устанавливающая соответствие между единицами измерений отрезков времени и пространства состояний.
Наглядное представление о том, как отображается состояние ДС на временной и пространственных осях дает рисунок 3. При таком способе отображения на координатных осях откладываются отрезки, пропорциональные изменениям количества состояний соответствующего признака (т.е. отображаются частоты появления состояний системы, не зависящие от того, как собственно состояния интерпретируются наблюдателем).

Умножив и разделив правую часть (4.3) на ![]() , получим:
, получим:
![]() (4.4)
(4.4)
Пусть ![]() - рассматриваемое
- рассматриваемое ![]() -мерное евклидово пространство и
-мерное евклидово пространство и ![]() - базис
- базис ![]() . Тогда с помощью проекций (4.4) дифференциал вектора состояния
. Тогда с помощью проекций (4.4) дифференциал вектора состояния ![]() можно отобразить в
можно отобразить в ![]() как линейную комбинацию векторов из
как линейную комбинацию векторов из ![]() :
:
![]()
![]() . (4.5)
. (4.5)
Выберем в качестве базиса ортонормированную систему векторов. В этом случае модуль вектора ![]() равен:
равен:
![]() . (4.6)
. (4.6)
Потребуем, чтобы система ограничений на движение ДС в собственном пространстве состояний была минимальной. Это означает, что направление и другие параметры движения не должны ограничиваться ничем кроме тождеств и неравенств цепи событий. Как видно из (4.5), при заданном базисе, движение всех подсистем ДС возможно только в положительном направлении его полуосей ![]() . Следовательно, задание конкретного базиса как системы констант вносит недопустимые ограничения, препятствующие, в частности, изотропности пространства. Поступим следующим образом. Будем считать базис, связанный с изображающей точкой системы, ортонормированным, произвольно ориентированным и масштабированным относительно некоторой системы декартовых координат. Геометрически это выглядит так (рис.4), как если бы в каждой точке пространства имелся свой локальный базис
. Следовательно, задание конкретного базиса как системы констант вносит недопустимые ограничения, препятствующие, в частности, изотропности пространства. Поступим следующим образом. Будем считать базис, связанный с изображающей точкой системы, ортонормированным, произвольно ориентированным и масштабированным относительно некоторой системы декартовых координат. Геометрически это выглядит так (рис.4), как если бы в каждой точке пространства имелся свой локальный базис ![]() , связанный линейным преобразованием с некоторым начальным ортогональным базисом
, связанный линейным преобразованием с некоторым начальным ортогональным базисом ![]() (в некотором смысле аналогично пространству Вейля[6]). Линейная комбинация векторов из
(в некотором смысле аналогично пространству Вейля[6]). Линейная комбинация векторов из ![]() вида (4.5) определяет приращение радиус – вектора подсистемы ДС в каждой точке пространства.
вида (4.5) определяет приращение радиус – вектора подсистемы ДС в каждой точке пространства.
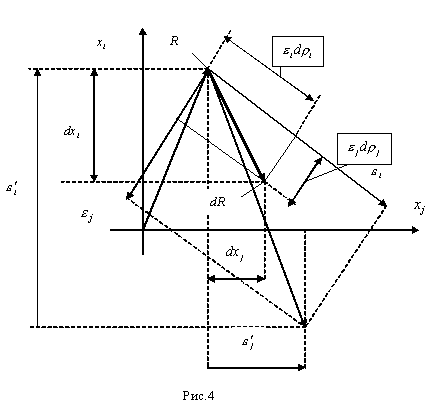
Раскладывая приращение вектора состояния системы ![]() по осям ортонормированного базиса
по осям ортонормированного базиса ![]() в точке
в точке ![]() , получаем для его компонент
, получаем для его компонент
![]() . (4.7)
. (4.7)
Раскладывая приращение вектора состояния системы по осям базиса ![]() , определяющего декартову систему координат
, определяющего декартову систему координат ![]() в виртуальном пространстве, получаем
в виртуальном пространстве, получаем
![]() , (4.8)
, (4.8)
где векторы ![]() базиса
базиса ![]() связаны с единичными векторами
связаны с единичными векторами ![]() линейным преобразованием.
линейным преобразованием.
Следовательно, вероятности состояний ![]() связаны с приращениями координат
связаны с приращениями координат ![]() линейным преобразованием вида:
линейным преобразованием вида:
![]() , (4.9)
, (4.9)
где ![]() - матрица линейного преобразования.
- матрица линейного преобразования.
Необходимым условием однородности и изотропности собственного виртуального пространства состояний динамической системы является ивариантность его метрики к линейным преобразованиям координат. Следовательно матрица ![]() должна быть ортогональной, а модуль вектора
должна быть ортогональной, а модуль вектора ![]() можно представить в инвариантном виде
можно представить в инвариантном виде
![]() . (4.10)
. (4.10)
Обозначим ![]() - бесконечно малый интервал между событиями в пространстве-времени ДС
- бесконечно малый интервал между событиями в пространстве-времени ДС
![]() . (4.11)
. (4.11)
Учитывая, что
![]() , (4.12)
, (4.12)
запишем (4.11) в виде
![]() (4.13)
(4.13)
В соответствии с первым неравенством цепи событий имеем:
![]() , (4.14)
, (4.14)
 . (4.15)
. (4.15)
Собственное виртуальное пространство – время общей ДС, также как и виртуальное пространство состояний, будем считать однородным и изотропным. Это означает инвариантность время – пространственного интервала ![]() к линейным преобразованиям в виртуальном пространстве – времени.
к линейным преобразованиям в виртуальном пространстве – времени.
Инвариантность время – пространственного интервала (4.11) и наличие ограничений (4.14, 4.15) – необходимые и достаточные условия для построения преобразований Лоренца и специальной теории относительности для общей системы, рассматриваемой в её собственном мире. Так как эта теория до сих пор базировалась на опытном материале, её невозможно было бы применить к абстрактной системе, чьи состояния не имеют отношения к пространственным объектам в нашем мире. Здесь же эта теория выглядит как статистический итог исчисления внешним или внутренним наблюдателем состояний общей динамической системы.
4.2. РАЗМЕРНОСТЬ ПРОСТРАНСТВА СОСТОЯНИЙ
Динамическая система “наш мир” является системой очень большой размерности. Тем не менее, наше восприятие ограничено тремя измерениями. Этот эмпирический факт до сих пор не получил какого-либо теоретического обоснования. При рассмотрении общей динамической системы мы не можем, опираясь на него, постулировать размерность пространства состояний, так как состояния абстрактной динамической системы, в общем случае, не отображены в физическом пространстве нашего мира. Поэтому нам придётся разработать математическую концепцию размерности пространства состояний общей системы, исходя из статистических закономерностей их распределения в цепи событий.
Рассмотрим пример классической (механической) системы в трёхмерном пространстве нашего мира. Система состоит из подсистем – материальных точек. Каждая такая подсистема определяется заданием трёх координат и трех импульсов в каждый момент времени. Для описания поведения всей системы, состоящей из ![]() материальных точек, в предельном случае требуется пространство
материальных точек, в предельном случае требуется пространство ![]() измерений.
измерений.
Теперь рассмотрим этот же пример в ином ракурсе. Пусть имеется ![]() - мерная динамическая система, о которой нам известно, что это система материальных точек, но не известно из какого количества точек она состоит. При этом материальная точка определена как объект, описываемый тремя переменными и их производными, удовлетворяющими некоторой системе ограничений. Положим для простоты
- мерная динамическая система, о которой нам известно, что это система материальных точек, но не известно из какого количества точек она состоит. При этом материальная точка определена как объект, описываемый тремя переменными и их производными, удовлетворяющими некоторой системе ограничений. Положим для простоты ![]() . Осуществим декомпозицию системы на подсистемы меньшей размерности, затем осуществим декомпозицию полученных подсистем и так до тех пор пока не получим такое множество подсистем, которые не могут быть подвергнуты декомпозиции без нарушения ограничений, которыми обусловлена их целостность. В нашем примере это ограничения, определяющие подсистемы как материальные точки. Следовательно, в предельном случае эксперимент с декомпозицией системы закончится её разбиением на
. Осуществим декомпозицию системы на подсистемы меньшей размерности, затем осуществим декомпозицию полученных подсистем и так до тех пор пока не получим такое множество подсистем, которые не могут быть подвергнуты декомпозиции без нарушения ограничений, которыми обусловлена их целостность. В нашем примере это ограничения, определяющие подсистемы как материальные точки. Следовательно, в предельном случае эксперимент с декомпозицией системы закончится её разбиением на ![]() материальных точек в пространстве трёх измерений. Рассмотренный пример допускает следующее обобщение. Если наблюдатель отображает динамическую систему в пространстве состояний в виде ансамбля точек, то размерность пространства равна размерности подсистемы, играющей роль точки. Эта размерность определяется как минимальная, при которой выполняются ограничения, обеспечивающие целостность подсистемы, и последняя обладает хоть одной степенью свободы. Минимальную размерность пространства состояний ДС определим следующим образом. Пусть имеется
материальных точек в пространстве трёх измерений. Рассмотренный пример допускает следующее обобщение. Если наблюдатель отображает динамическую систему в пространстве состояний в виде ансамбля точек, то размерность пространства равна размерности подсистемы, играющей роль точки. Эта размерность определяется как минимальная, при которой выполняются ограничения, обеспечивающие целостность подсистемы, и последняя обладает хоть одной степенью свободы. Минимальную размерность пространства состояний ДС определим следующим образом. Пусть имеется ![]() - мерная подсистема ДС вида (4.1). Пусть на вероятности её состояний наложено
- мерная подсистема ДС вида (4.1). Пусть на вероятности её состояний наложено ![]() ограничений
ограничений
 (4.16)
(4.16)
Если ![]() то, решая систему уравнений (4.16), получим
то, решая систему уравнений (4.16), получим ![]() (
(![]() ) В общем случае, при
) В общем случае, при ![]() решения (4.16) не существует. При
решения (4.16) не существует. При ![]() с учетом (2.14) получим
с учетом (2.14) получим ![]() Следовательно, минимальная размерность, при которой подсистема обладает свободой движения
Следовательно, минимальная размерность, при которой подсистема обладает свободой движения ![]() . При декомпозиции ДС размерности
. При декомпозиции ДС размерности ![]() на подсистемы, каждая из которых удовлетворяет
на подсистемы, каждая из которых удовлетворяет ![]() ограничениям, получим динамические подсистемы размерности не менее чем
ограничениям, получим динамические подсистемы размерности не менее чем ![]() . Если
. Если ![]() - минимально возможное число ограничений, то подсистемы в пространстве состояний размерности
- минимально возможное число ограничений, то подсистемы в пространстве состояний размерности ![]() играют роль материальных точек. Само собой разумеется, что в число минимально возможных ограничений входят лишь те, которые обусловлены внутренними статистическими закономерностями цепи событий. Первое такое ограничение на изолированную
играют роль материальных точек. Само собой разумеется, что в число минимально возможных ограничений входят лишь те, которые обусловлены внутренними статистическими закономерностями цепи событий. Первое такое ограничение на изолированную ![]() - тую подсистему накладывается условием нормировки
- тую подсистему накладывается условием нормировки
![]() . (4.17)
. (4.17)
Для вывода второго ограничения запишем пространственно – временной интервал в виде
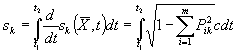 . (4.18)
. (4.18)
Из инвариантности подынтегральной функции следует существование интеграла движения
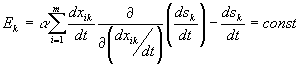 , (4.19)
, (4.19)
где: ![]() - постоянный коэффициент.
- постоянный коэффициент.
Выразив производные от координат через вероятности в соответствии с (4.9), получим
![]() . (4.20)
. (4.20)
Это равенство накладывает второе ограничение на вероятности состояний ![]() - той подсистемы. Если учитывать в качестве ограничений и другие интегралы движения, то получим систему с числом степеней свободы больше единицы. Следовательно, подсистема, играющая роль материальной точки в пространстве состояний ДС, имеет размерность, равную трём (три класса событий
- той подсистемы. Если учитывать в качестве ограничений и другие интегралы движения, то получим систему с числом степеней свободы больше единицы. Следовательно, подсистема, играющая роль материальной точки в пространстве состояний ДС, имеет размерность, равную трём (три класса событий ![]() ). Поэтому собственное пространство состояний абстрактной системы, воспринимаемой наблюдателем в виде ансамбля материальных точек, имеет размерность равную трём. Трёхмерность нашего мира можно рассматривать как эмпирическое подтверждение этого теоретического вывода.
). Поэтому собственное пространство состояний абстрактной системы, воспринимаемой наблюдателем в виде ансамбля материальных точек, имеет размерность равную трём. Трёхмерность нашего мира можно рассматривать как эмпирическое подтверждение этого теоретического вывода.
5. ПОЛЕ В СОБСТВЕННОМ ПРОСТРАНСТВЕ ДИНАМИЧЕСКОЙ СИСТЕМЫ
Как известно, наиболее общая формулировка закона движения механических систем в нашем мире дается принципом наименьшего действия (или принципом Гамильтона). Этим же принципом руководствуются в физике при выводе законов взаимодействия частиц с полем и уравнений поля. С математической точки зрения принцип наименьшего действия является постулатом, сформулированным как эмпирическое обобщение большого числа наблюдений за поведением механических систем. В теории оптимального управления вариационные принципы базируются на идее существования целевого функционала, конкретный вид которого обусловлен целью задачи управления поведением системы. Эмпирическая основа, а также отсутствие видимой цели эволюции, не позволяют без должного обоснования использовать эти принципы для формулировки закона движения общей ДС в её собственном мире. Тем не менее, для того чтобы иметь возможность использовать хорошо разработанный математический аппарат, желательно сформулировать подобный вариационный принцип применительно к рассматриваемым системам без ссылки на результаты наблюдений в нашем мире.
5.1. ПРИНЦИП НАИБОЛЕЕ ВЕРОЯТНОЙ ЦЕПИ СОБЫТИЙ.
Эволюцию общей ДС можно охарактеризовать каким-то законом. Для внешнего наблюдателя это закон распределения состояний в цепи событий наблюдаемой ДС. Каждый такой закон обусловлен действующими в отношении рассматриваемой системы ограничениями. Последние могут регламентировать сочетания различных признаков в цепи событий, или (и) соотношение их количеств. В первом случае имеется, как бы набор грамматических правил, согласно которым формируются объекты состояний подсистем ДС, что можно интерпретировать как их взаимодействие посредством сообщений. Ограничения второго типа, базирующиеся на тождествах и неравенствах цепи событий, рассмотрены в предыдущих разделах. Они позволяют представить ДС в виде ансамбля материальных точек в собственном трехмерном пространстве и во времени.
При заданных ограничениях на распределение состояний можно указать такое распределение, которому удовлетворяет наибольшее количество возможных цепей событий. Системы с таким распределением состояний встречаются чаще в процессе наблюдений за окружающим миром, иными словами, являются наиболее вероятными.
Следовательно, если мы хотим получить наиболее вероятные законы взаимодействия подсистем общей ДС, то должны руководствоваться при их выводе принципом наиболее вероятной цепи событий. Этот принцип универсален, как для систем, взаимодействующих посредством сообщений (ограничения первого типа), так и для ансамбля материальных точек (ограничения второго типа), взаимодействующих, как будет показано ниже, посредством силового поля в собственном пространстве ДС.
Ранее (раздел 3), при исследовании неравенств цепи событий, было установлено, что логарифмическим эквивалентом количества возможных реализаций отрезка ![]() цепи событий, является энтропия
цепи событий, является энтропия ![]() .
.
Варьируя ансамбль признаков в пределах, обусловленных ограничениями, можно добиться такого распределения состояний на отрезке цепи ![]() , при котором энтропия
, при котором энтропия ![]() будет максимальной и, следовательно, цепь событий
будет максимальной и, следовательно, цепь событий ![]() наиболее вероятной.
наиболее вероятной.
Выразим теперь принцип наиболее вероятной цепи событий математически в таком виде, чтобы из него можно было вывести уравнения движения материальных точек в функции их распределения в собственном пространстве ДС. Устремляя количество состояний на конечном отрезке времени к бесконечности, получаем возможность, в предельном случае, рассматривать собственное пространство – время ДС как континуум. При этом уравнения движения сводятся к дифференциальным уравнениям, а взаимодействие подсистем с системой можно рассматривать как взаимодействие частиц с силовым полем, распределённым в собственном пространстве ДС.
Запишем в общем виде
 (5.1)
(5.1)
Учитывая зависимость вероятностей состояний от координат и их производных, данную задачу следует рассматривать как общую задачу Лагранжа. Для её решения необходимо найти безусловный экстремум от интеграла
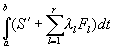 , (5.2)
, (5.2)
где ![]() - некоторые функции времени.
- некоторые функции времени.
Задача (5.2) может быть упрощена и сведена к известной в вариационном исчислении изопериметрической задаче [5] в тех случаях, когда систему ограничений удается свести к виду:
 (5.3)
(5.3)
В этом случае ![]() - константы и для решения задачи (5.1) необходимо найти безусловный экстремум от интеграла
- константы и для решения задачи (5.1) необходимо найти безусловный экстремум от интеграла
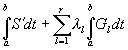 . (5.4)
. (5.4)
Учитывая двойственный характер экстремальных задач, замечаем, что максимуму функционала (5.4) соответствует минимум функционала
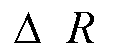 . (5.5)
. (5.5)
В этом интеграле первый член можно рассматривать как действие для поля, а последующие члены, как действие для частиц и их взаимодействия с полем системы.
Следовательно, принцип наименьшего действия, представленный функционалом (5.5), можно рассматривать как частный случай принципа наиболее вероятной цепи событий.
5.2. СИСТЕМА ОГРАНИЧЕНИЙ
В предыдущих разделах рассматривалась система без учета её взаимодействия с другими системами. Изоляция системы формально достигалась тем, что учитывались только её собственные состояния. Математически это выражалось условием нормировки, которое для изолированной системы имеет вид (2.8). Рассматривая ДС как ансамбль взаимодействующих материальных точек необходимо учитывать состояния всех её подсистем. При этом условие нормировки следует записывать в виде
![]() , (5.6)
, (5.6)
где: ![]() - вероятность k – той подсистемы как целого на рассматриваемом отрезке цепи.
- вероятность k – той подсистемы как целого на рассматриваемом отрезке цепи.
Также добавляется условие нормировки для системы в целом
![]() . (5.7)
. (5.7)
Для того чтобы математические выражения для приращений координат и время – пространственного интервала записывались одинаково, как для взаимодействующих подсистем ДС, так и для изолированной системы перепишем их в виде
![]() , (5.8)
, (5.8)
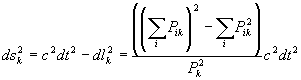 . (5.9)
. (5.9)
Запишем уравнения (4.9) в развёрнутом виде для ![]() -той подсистемы
-той подсистемы
![]() . (5.10)
. (5.10)
Суммируя правые и левые части выражения (5.10), получим
![]() , (5.11)
, (5.11)
где:
![]() .
.![]() (5.12)
(5.12)
Интегрируя правую и левую части равенства (5.11), получим первое ограничение в виде
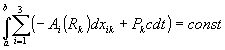 . (5.13)
. (5.13)
Второе ограничение на k – тую подсистему уже было сформулировано выше
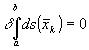 . (5.14)
. (5.14)
Условие нормировки (5.8) для системы в целом запишем в виде
 . (5.15)
. (5.15)
5.4. ДЕЙСТВИЕ ДЛЯ СОБСТВЕННОГО ПОЛЯ ДИНАМИЧЕСКОЙ СИСТЕМЫ.
С учетом ограничений (5.13, 5.14,5.15) функционал действия (5.5) перепишем в виде
![]() . (5.16)
. (5.16)
При варьировании этого функционала по координатам первые два слагаемых можно не учитывать, так как в них под интегралами находятся полные дифференциалы функций координат и времени (калибровочная инвариантность). Получаемые при этом экстремали представляют собой ансамбль траекторий материальных точек в заданном поле системы.
Последнее слагаемое есть та часть действия ![]() , которая зависит только от свойств подсистем (частиц), т.е. действие для свободных частиц
, которая зависит только от свойств подсистем (частиц), т.е. действие для свободных частиц
![]() , (5.17)
, (5.17)
где: ![]() - коэффициент, отождествляемый с массой частицы.
- коэффициент, отождествляемый с массой частицы.
Так как ![]() - положительно определённый скаляр, то и масса частицы есть величина всегда положительная.
- положительно определённый скаляр, то и масса частицы есть величина всегда положительная.
Сумма второго и третьего слагаемого в (5.16) по аналогии с теорией электромагнитного поля есть та часть действия ![]() , которая обусловлена взаимодействием между частицами и полем
, которая обусловлена взаимодействием между частицами и полем
![]() , (5.18)
, (5.18)
где: ![]() - коэффициент, отождествляемый с зарядом частицы,
- коэффициент, отождествляемый с зарядом частицы, ![]() - векторный потенциал поля ДС в той точке собственного пространства и времени, в которой находится соответствующая подсистема,
- векторный потенциал поля ДС в той точке собственного пространства и времени, в которой находится соответствующая подсистема,
![]() - скалярный потенциал.
- скалярный потенциал.
Так как в подынтегральном выражении при произвольном поле и движении частицы скалярное произведение![]() может иметь различные знаки, а в исходном ограничении это положительно определённая величина (вероятность), то заряд
может иметь различные знаки, а в исходном ограничении это положительно определённая величина (вероятность), то заряд ![]() должен иметь разные знаки в зависимости от знака указанного скалярного произведения.
должен иметь разные знаки в зависимости от знака указанного скалярного произведения.
Итак, мы видим, что общая динамическая система может рассматриваться в собственном мире как ансамбль заряженных частиц, взаимодействующих с калибровочным полем, адекватным известному нам электромагнитному полю.
Сумма ![]() - действие для зарядов в поле. Подынтегральное выражение в этой сумме есть функция Лагранжа для заряда в электромагнитном поле
- действие для зарядов в поле. Подынтегральное выражение в этой сумме есть функция Лагранжа для заряда в электромагнитном поле
![]() . (5.19)
. (5.19)
Варьируя действие по координатам, получим известные тензорные уравнения движения зарядов в электромагнитном поле
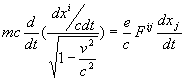 , (5.20)
, (5.20)
где индексы ![]() независимо пробегают значения 0,1,2,3;
независимо пробегают значения 0,1,2,3; ![]() - антисимметрический тензор, называемый тензором электромагнитного поля
- антисимметрический тензор, называемый тензором электромагнитного поля
![]() . (5.21)
. (5.21)
Первое слагаемое в (5.16)
![]()
![]()
есть та часть действия, которая зависит только от свойств самого поля. Для того чтобы получить замкнутую систему уравнений эволюции общей динамической системы необходимо выразить скорость производства энтропии ![]() в единице объёма через величины, характеризующие движение подсистем. Схема рассуждений, позволяющая в явном виде выразить действие
в единице объёма через величины, характеризующие движение подсистем. Схема рассуждений, позволяющая в явном виде выразить действие ![]() для случая электромагнитного поля, хорошо известна [7]. Она опирается на следующие утверждения:
для случая электромагнитного поля, хорошо известна [7]. Она опирается на следующие утверждения:
а) функция Лагранжа в подынтегральном выражении есть положительно определённый скаляр;
б) она не может быть функцией потенциалов, так как те не определены однозначно;
в) поле подчиняется принципу суперпозиции.
Пункты а) и в) в теории поля постулируются на основании эмпирических обобщений.
Положительная определённость функции Лагранжа связывается с необходимостью ![]() иметь минимум согласно принципу наименьшего действия. Принцип суперпозиции электромагнитных полей есть опытно установленный факт. В развиваемой здесь теории поля эти утверждения должны быть логическими следствиями тождеств и неравенств цепи событий ДС, так как эта теория применима к описанию собственных миров любых динамических систем. Пункт а) непосредственно следует из второго неравенства (3.9) цепи событий. Пункт в) докажем, опираясь на свойство аддитивности функции распределения состояний.
иметь минимум согласно принципу наименьшего действия. Принцип суперпозиции электромагнитных полей есть опытно установленный факт. В развиваемой здесь теории поля эти утверждения должны быть логическими следствиями тождеств и неравенств цепи событий ДС, так как эта теория применима к описанию собственных миров любых динамических систем. Пункт а) непосредственно следует из второго неравенства (3.9) цепи событий. Пункт в) докажем, опираясь на свойство аддитивности функции распределения состояний.
Пусть цепь событий k – той подсистемы представляет собой объединение двух цепей событий соответствующих подсистем
![]() , (5.22)
, (5.22)
тогда вероятность k – той подсистемы равна сумме вероятностей составляющих подсистем
![]() . (5.23)
. (5.23)
Векторный потенциал поля по определению (5.12) является линейной функцией вероятности.
Так как базис зависит только от выбора точки в пространстве, то векторный потенциал в точке ![]() равен
равен
![]()
![]() . (5.24)
. (5.24)
Следовательно, векторный потенциал поля, создаваемого сложной подсистемой равен сумме (геометрической) векторных потенциалов составляющих подсистем.
Скалярный потенциал подчиняется принципу суперпозиции, так как он также линейно зависит от вероятности (первый член в формуле скалярного потенциала, нарушающий аддитивность из-за множителя ![]() не существенен для поля вследствие калибровочной инвариантности). Таким образом, принцип суперпозиции для собственного поля общей ДС доказан и, следовательно, по аналогии с известным результатом из теории электромагнитного поля действие
не существенен для поля вследствие калибровочной инвариантности). Таким образом, принцип суперпозиции для собственного поля общей ДС доказан и, следовательно, по аналогии с известным результатом из теории электромагнитного поля действие ![]() должно иметь вид
должно иметь вид
![]() ,
, ![]() . (5.25)
. (5.25)
Численное значение ![]() зависит от выбора единиц для измерения поля.
зависит от выбора единиц для измерения поля.
Поскольку действие для общей ДС имеет точно такой же вид, как и действие для электромагнитного поля с находящимися в нём зарядами, то можно утверждать, что в собственном мире динамической системы имеют место все известные электромагнитные явления.
Всё изложенное выше относится к виртуальному миру ДС. Реальный собственный мир динамической системы это мир, воспринимаемый наблюдателем, связанным с какой – то из её подсистем.
Движение подсистем ДС, как это видно из уравнений (5.20), в общем случае не равномерно и не прямолинейно. Следовательно, преобразование, связывающее виртуальную и реальную системы отсчета, также не линейно. Переход к криволинейным координатам пространства – времени, согласно принципу эквивалентности, соответствует дополнительному взаимодействию подсистем ДС с каким – то гравитационным полем. При этом локальный базис в каждой точке пространства – времени обусловлен не только векторными потенциалами калибровочного поля (как в виртуальном мире), но и переменной метрикой (потенциалами гравитационного поля) реального пространства – времени, также определяемых из принципа наиболее вероятной цепи событий.
6. СУПЕРВИЗОРНЫЕ ПРЕОБРАЗОВАНИЯ
Пусть имеется некоторая динамическая система, которую мы наблюдаем в виде временого ряда абстрактных, по отношению к нашему пространству, состояний. Понятно, что собственный мир этой системы не доступен нашему непосредственному наблюдению. Однако из изложенного выше следует возможность математически реконструировать образ собственного мира, наблюдаемой системы, по распределению состояний в её временном ряду.
Представляет интерес также и обратная задача: математически реконструировать, недоступную непосредственному наблюдению извне, цепь событий нашего мира по распределению материальных точек в наблюдаемом пространстве.
Математическое преобразование распределения вероятностей цепи событий ДС в распределение координат объектов её собственного мира будем называть прямым супервизорным преобразованием образа собственного мира.
Математическое преобразование распределения координат объектов собственного мира ДС в распределение вероятностей её цепи событий будем называть обратным супервизорным преобразованием образа собственного мира.
В данной работе ограничимся выводом супервизорных преобразований виртуального мира. Для распространения полученных результатов на реальные собственные миры динамических систем необходимо перейти к криволинейным координатам пространства – времени, используя известный математический аппарат общей теории относительности.
Для вывода искомых преобразований сопоставим уравнения движения материальных точек с тождествами цепи событий.
Уравнения движения материальных точек (зарядов) в собственном поле системы, согласно установленной выше аналогии с электромагнитным полем, можно записать в трёхмерном виде.
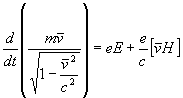 , (6.3)
, (6.3)
где: ![]() - векторы напряженностей электрического и магнитного полей, составленные из компонент тензора электромагнитного поля
- векторы напряженностей электрического и магнитного полей, составленные из компонент тензора электромагнитного поля ![]() .
.
Обозначим  - массу движущейся частицы ( в отличие от массы покоя -
- массу движущейся частицы ( в отличие от массы покоя -![]() ).
).
Раскрывая производную в левой и векторное произведение в правой части уравнения (6.3), получим
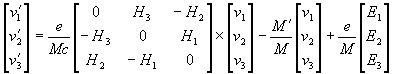 . (6.4)
. (6.4)
В компактной записи это уравнение имеет вид
![]() . (6.5)
. (6.5)
Запишем тождества (2.14), выделив в системе материальную точку, и обозначим её состояния и переходы индексами ![]() , пробегающими независимо друг от друга значения 1,2,3 (все иные значения будем обозначать индексом
, пробегающими независимо друг от друга значения 1,2,3 (все иные значения будем обозначать индексом ![]() )
)
![]()
![]()
![]() . (6.6)
. (6.6)
Обозначив ![]()
![]() , получим
, получим
![]()
 . (6.7)
. (6.7)
Подставим в эти тождества вероятности ![]() , выраженные через скорости изменения координат материальной точки
, выраженные через скорости изменения координат материальной точки![]() согласно (4.9)
согласно (4.9)
![]() , (6.8)
, (6.8)
где:
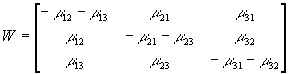 , (6.9)
, (6.9)
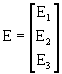 (6.10)
(6.10)
С учётом ортогональности матрицы ![]() тождествам (6.8) можно придать вид
тождествам (6.8) можно придать вид
![]() . (6.11)
. (6.11)
Матрицу в скобках представим в виде суммы антисимметрической ![]() и симметрической
и симметрической ![]() матриц
матриц
![]() , (6.12)
, (6.12)
где:
![]()
![]()
![]() , (6.13)
, (6.13)
![]()
![]()
![]() . (6.14)
. (6.14)
Из равенства левых частей уравнений (6.5) и (6.12) следует равенство их правых частей. Но так как (6.12) является тождеством, это равенство должно выполняться почленно. Приравнивая члены с одинаковыми показателями степени ![]() , получим следующие два уравнения
, получим следующие два уравнения
![]() , (6.15)
, (6.15)
![]() . (6.16)
. (6.16)
Однако, не трудно доказать, что первое из этих уравнений распадается на два уравнения. Действительно, так как ![]() и
и ![]() антисимметрические матрицы с нулевыми диагональными элементами, то разность
антисимметрические матрицы с нулевыми диагональными элементами, то разность ![]() - также является антисимметрической матрицей с нулевыми диагональными элементами, которая в сумме с симметрической матрицей
- также является антисимметрической матрицей с нулевыми диагональными элементами, которая в сумме с симметрической матрицей ![]() (где
(где ![]() - единичная матрица) может давать нуль лишь в том случае, когда все элементы главной диагонали последней равны нулю. Как видно из (6.14), в общем случае элементы главной диагонали
- единичная матрица) может давать нуль лишь в том случае, когда все элементы главной диагонали последней равны нулю. Как видно из (6.14), в общем случае элементы главной диагонали ![]() не равны друг другу и не равны нулю.
не равны друг другу и не равны нулю.
Следовательно, имеем три базовых уравнения для вывода супервизорных преобразований
![]()
![]() , (6.17)
, (6.17)
![]() , (6.18)
, (6.18)
![]() . (6.19)
. (6.19)
Для того чтобы найти коэффициенты преобразования ![]() примем во внимание ортогональность матрицы
примем во внимание ортогональность матрицы ![]() , (что является математическим выражением однородности и изотропности собственного пространства состояний), а также выражение (5.12) для компонент векторного потенциала собственного поля системы. Получим следующую систему уравнений
, (что является математическим выражением однородности и изотропности собственного пространства состояний), а также выражение (5.12) для компонент векторного потенциала собственного поля системы. Получим следующую систему уравнений
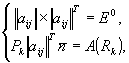 (6.20)
(6.20)
где: ![]() - матрица – столбец с единичными элементами.
- матрица – столбец с единичными элементами.
В развёрнутом виде эта система насчитывает шесть уравнений второго и три первого порядка – ровно столько, сколько необходимо для того, чтобы выразить девять коэффициентов ![]() через компоненты
через компоненты ![]() векторного потенциала собственного поля ДС.
векторного потенциала собственного поля ДС.
6.1. ПРЯМОЕ СУПЕРВИЗОРНОЕ ПРЕОБРАЗОВАНИЕ
Предполагаем, что нам известна цепь событий динамической системы, распределение состояний которой требуется преобразовать в распределение координат и импульсов материальных точек в её собственном мире. Это значит, что известны все плотности вероятностей переходов ![]() для каждого момента времени
для каждого момента времени ![]() . Кроме того, в цепи указаны подмножества событий для всех состояний материальной точки – объекта преобразования
. Кроме того, в цепи указаны подмножества событий для всех состояний материальной точки – объекта преобразования ![]() .
.
Из матричных уравнений (6.17, 6.19) имеем систему шести нелинейных дифференциальных уравнений в частных производных относительно потенциалов поля ![]() ,
, ![]() и их производных
и их производных ![]() по координатам собственного пространства. Из уравнения (6.18), получим три собственных значения
по координатам собственного пространства. Из уравнения (6.18), получим три собственных значения ![]() ,
, ![]() и три подпространства собственных векторов скорости материальной точки. Все собственные значения действительны вследствие симметричности матрицы
и три подпространства собственных векторов скорости материальной точки. Все собственные значения действительны вследствие симметричности матрицы ![]() .
.
Для того, чтобы найти значения массы и заряда материальной точки, воспользуемся ограничениями (5.13, 5.14, 5.15), переписав их в виде
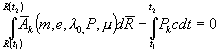 , (6.21)
, (6.21)
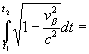
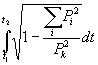 , (6.22)
, (6.22)
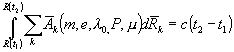 . (6.23)
. (6.23)
Решая эту систему уравнений при заданных граничных условиях, а также, учитывая
 , (6.24)
, (6.24)
найдём для каждого собственного вектора ![]() , соответствующие значения массы и заряда материальной точки
, соответствующие значения массы и заряда материальной точки ![]() , а также значения множителя
, а также значения множителя ![]() .
.
Таким образом, одной минимальной подсистеме цепи событий соответствует три подпространства материальных точек, отличающихся массой, зарядом и импульсом.
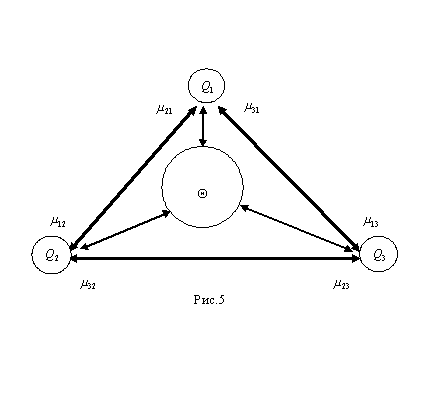
Предполагаем, что нам известно поле в собственном пространстве динамической системы, а также значения массы, заряда и скорости материальной точки, для которой осуществляется преобразование. Требуется найти распределение состояний соответствующей подсистемы в цепи событий рассматриваемой системы. Граф переходов подсистемы “материальная точка” в цепи событий показан на рисунке 3, где обозначено: ![]() - состояния подсистемы,
- состояния подсистемы, ![]() - множество состояний ДС, дополнительных к выделенным состояниям подсистемы. Стрелками показаны переходы между состояниями.
- множество состояний ДС, дополнительных к выделенным состояниям подсистемы. Стрелками показаны переходы между состояниями.
Так как распределение вероятностей состояний подсистемы описывается уравнением (6.7), то задача сводится к отысканию девяти переменных ![]() и
и ![]() . Из (6.17) и (6.19) имеем шесть уравнений, связывающих эти переменные с параметрами поля и материальной точки. Кроме того, имеются уравнения движения материальной точки, с помощью которых координаты собственного пространства ДС могут быть выражены через параметр
. Из (6.17) и (6.19) имеем шесть уравнений, связывающих эти переменные с параметрами поля и материальной точки. Кроме того, имеются уравнения движения материальной точки, с помощью которых координаты собственного пространства ДС могут быть выражены через параметр ![]() . Недостающие три уравнения получим из (6.18). Для этого приведём матрицу
. Недостающие три уравнения получим из (6.18). Для этого приведём матрицу ![]() к диагональному виду. Эта задача заведомо разрешима, так как
к диагональному виду. Эта задача заведомо разрешима, так как ![]() - симметрическая матрица. Из равенства
- симметрическая матрица. Из равенства
![]() (
(![]() )
)![]() , (6.25)
, (6.25)
где ![]() - ортогональная диагонализирующая матрица, получаем три уравнения, связывающие искомые переменные с параметрами поля системы и модулем скорости материальной точки.
- ортогональная диагонализирующая матрица, получаем три уравнения, связывающие искомые переменные с параметрами поля системы и модулем скорости материальной точки.
7. ЗАКЛЮЧЕНИЕ.
Результаты проведенного исследования доказывают существование собственных миров динамических систем, аналогичных нашему миру. Исследованные аналогии пока исчерпываются некоторыми физическими законами, определяющими свойства пространства, времени и поля. Однако есть основания предполагать, что они простираются гораздо дальше. Так, например, из принципа наиболее вероятной цепи событий (максимум энтропии), при учете различных ограничений на вероятности состояний, можно вывести [8] уравнения равновесной и неравновесной термодинамики, уравнения состояния вещества.
Что же нам дает теория собственных миров динамических систем? С одной стороны, появляется возможность сравнительного анализа поведения внешне не имеющих ничего общего систем, а также математического исследования Кантовской “вещи в себе”. С другой стороны, некоторые физические законы нашего мира, традиционно считавшиеся эмпирическими, получают объяснение как следствия линейной упорядоченности цепи событий общей динамической системы.
Но предлагаемая теория также порождает очень серьёзную проблему в философии. Смысл её состоит в том, что любая динамическая система, в том числе нематериальная с нашей точки зрения (например: абстрактный автомат, программа, мысль) обладает в собственном мире всеми атрибутами материи: веществом и полем. Здесь могут возразить, что “действующая” во времени программа всегда предполагает некоторый материальный носитель. Однако, как следует из вышеизложенного, ни количественно, ни качественно материальность этого носителя не может быть соотнесена с материальностью собственного мира порождаемой им системы.
И в заключение рассмотрим с позиций изложенной теории одно из самых интригующих противоречий современной физики, состоящее в том, что эволюция замкнутой системы с точки зрения термодинамики необратима, притом, что её поведение, как системы материальных точек, описывается обратимыми во времени уравнениями гамильтоновой динамики.
Запишем уравнения движения материальной точки в виде
![]() . (7.1)
. (7.1)
Преобразуем обратным супервизорным преобразованием распределение её координат и скоростей в распределение вероятностей состояний в цепи событий общей динамической системы. Получим распределение трёх вероятностей ![]() ,
,![]()
![]() , которые согласно второму неравенству цепи событий, изменяются необратимо. Прямое супервизорное преобразование ставит в соответствие этому распределению множество калибровочных полей и траекторий.
, которые согласно второму неравенству цепи событий, изменяются необратимо. Прямое супервизорное преобразование ставит в соответствие этому распределению множество калибровочных полей и траекторий.
Следовательно, на вопросы, поставленные И. Пригожиным [9]: “можно ли вывести оператор энтропии в рамках динамического описания” и “может ли марковский процесс появиться при обратимой во времени динамике”, можно дать положительный ответ. Формальные основания для этого даёт математический аппарат супервизорных преобразований.
Рассмотрим содержательный смысл проблемы микроскопической необратимости. С точки зрения динамического описания материальной точки, задание начальных условий полностью определяет её траекторию. До сих пор априори считалось, что вся информация об эволюции подсистемы “материальная точка”, заключена в её траектории (волновой функции). Поэтому движение материальной точки, как бы, не создавало новой информации, (энтропия оставалась неизменной). Отсюда следовал вывод об обратимости эволюции отдельно взятой подсистемы “материальная точка”. На уровне микроописания динамическая система оказывалась инвариантной к “стреле времени”.
Согласно известной теореме Пуанкаре, в рамках гамильтоновой динамки не существует функции координат и импульсов, которая обладала бы свойствами функции Ляпунова. Этот вывод Пуанкаре, как доказал Б.Мисра [9], остаётся в силе при любом усреднении функций распределения в фазовом пространстве.
Новая точка зрения состоит в том, что материальная точка, как динамический объект в пространстве, является лишь частным образом динамической подсистемы. Как было показано выше, её траектория полностью определяется распределением количеств состояний в цепи событий. Но знание распределения количеств состояний не достаточно для детального восстановления порядка их следования. Следовательно, детерминированная траектория не означает детерминированной эволюции. Задание начальных условий предопределяет лишь количество возможных “сообщений” – последовательностей состояний в цепи событий, но не сами последовательности. Эволюция подсистемы информационно богаче движения отображающей её точки в пространстве. Эволюция материальной точки сопровождается производством информации для внешнего наблюдателя. Если извне не накладываются специальные ограничения на содержание сообщений в цепи событий, то в каждый момент времени невозможно предсказать следующее состояние. А значит, эволюция материальной точки необратима постольку, поскольку непредсказуемо содержание сообщения, заключённого в последовательности состояний цепи её событий. Эта неопределённость возрастает с увеличением количества событий, т. е. с течением времени. Рассматривая замкнутую динамическую систему, как целое (т.е. учитывая все последовательности состояний в цепи событий), получаем в соответствии с (3.9, 5.16, 5.25)
![]() , (7.2)
, (7.2)
где интегрирование производится по всему объёму пространства.
Таким образом, калибровочное поле динамической системы эволюционирует необратимо. Здесь нет никакого противоречия с теоремой Пуанкаре - Мисры, поскольку итеграл (7.2) не зависит от координат и импульсов материальных точек. Повидимому, приращение энтропии следует рассматривать как сумму двух приращений
![]() , (7.3)
, (7.3)
где: ![]() элемент фазового объёма; первое слагаемое соответствует приращению энтропии вследствие увеличения количества состояний системы; второе слагаемое соответствует приращению энтропии вследствие увеличения количества событий в системе. В консервативных системах фазовый объём не изменяется, следовательно первое слагаемое обращается в нуль – информация для собственного мира не производится. Однако, для внешнего наблюдателя увеличивающаяся цепь событий производит новую информацию. Следовательно, второе слагаемое не обращается в нуль. Рассматривая динамическую систему только как ансамбль частиц в собственном мире, мы утрачиваем её информационное содержание. Цена такого упрощения – искажение смысла времени.
элемент фазового объёма; первое слагаемое соответствует приращению энтропии вследствие увеличения количества состояний системы; второе слагаемое соответствует приращению энтропии вследствие увеличения количества событий в системе. В консервативных системах фазовый объём не изменяется, следовательно первое слагаемое обращается в нуль – информация для собственного мира не производится. Однако, для внешнего наблюдателя увеличивающаяся цепь событий производит новую информацию. Следовательно, второе слагаемое не обращается в нуль. Рассматривая динамическую систему только как ансамбль частиц в собственном мире, мы утрачиваем её информационное содержание. Цена такого упрощения – искажение смысла времени.
СПИСОК ЛИТЕРАТУРЫ
СОБСТВЕННЫЕ МИРЫ ДИНАМИЧЕСКИХ СИСТЕМ.
А. Заславский.
АННОТАЦИЯ
Рассматривается общая динамическая система как цепь абстрактных событий. Вводится понятие собственного пространства – времени динамической системы, в котором расстояние измеряется количеством состояний, отделяющих одно событие от другого, а время – количеством событий. Разработан в общих чертах математический аппарат преобразований, позволяющих отображать распределение состояний цепи событий в распределение силового поля и материальных точек (и наоборот) в собственном пространстве – времени общей динамической системы.
INTRINSIC WORLDS OF DYNAMIC SYSTEMS
A. Zaslavsky
ANNOTATION
Dynamic system is treated as abstract chain of events. The concept of intrinsic space – time of dynamic system is introduced, where the distance is measured by the number of status separating one event from another, and time is measured by the number of events within a system. The system of mathematic transformation is designed in outline. These transformations make possible to map over the distribution of status of events chain in the distribution of field and material points (and on the contrary) within the intrinsic space – time of common dynamic system.