© А.М.Заславский

Нет такого первого начала, которое
само по себе было бы непознаваемым,
не схватываемым вспышкой озарения.
А.Уайтхед: “Процесс и реальность”

Ньютон полагал, что он “гипотез не измышляет”. Галилей также предпочитал строгие исследования туманным предположениям. Но, во многом благодаря их раскованному воображению, был заложен фундамент восьмого чуда света – здания современной физики. Его архитектура отличается математической строгостью, простотой и изяществом. Для чего возведен этот храм? В точном соответствии с замыслом первостроителей – для ответа на вопрос, каков наш мир. Однако, сколь бы тщательно мы ни исследовали это великолепное сооружение, нам не найти ответы на вопросы, почему наш мир таков как он есть, может ли он быть устроен иначе. Задайте эти вопросы современным строителям и служителям храма – физикам. Вы получите строгий исчерпывающий ответ, гипотез не измышляем.

Идея придать метафизике характер точной науки, со времён Аристотеля до наших дней, периодически завладевает умами исследователей самого различного профиля. Даже Мартин Хайдеггер, отвергая математику, как мерило философского знания, вынужден признать: “Декарт, определивший основополагающую установку новоевропейской философии, - чего другого хотел он, как не придать философской истине математический характер и вывести человечество из сомнения и неясности? От Лейбница дошло изречение: Sans les mathematiques on ne penetre point au fond de la Metaphysique, “без математики не проникнуть в основание метафизики”. Вот, кажется, самое глубокое и самое ёмкое подтверждение того, что люди естественным образом выставляют как абсолютную истину в философии для каждого” [1].

Среди работ последнего времени следует отметить проект Principia Cybernetica (В. Турчин, К. Джослин, Ф. Хейлиген) [2]. Его авторы поставили своей целью создание языка философии, адекватного по точности алгоритмическим языкам. Кибернетический подход к метафизике декларируется в работах Валентина Турчина "Cybernetic Metaphysics" [3] и "Cybernetic Ontology of Action" [4].

Одним из основных предметов исследования метафизики является время. Пожалуй, за всю историю научной мысли не было более интригующей и неприступной проблемы.

Физика имеет дело с объектами наблюдаемого мира и их отношениями (физическими явлениями). Сами эти объекты не могут быть определены иначе, чем посредством взаимных отношений. Примером тому является любой толковый словарь. Физика систематизирует и упорядочивает отношение на множестве объектов наблюдаемого мира, создавая ограниченное множество универсальных определяющих высказываний, которые принято называть законами природы. Основания физики можно рассматривать как некую аксиоматическую систему. Однако, Гёдель показал, что методами, которые могут быть представлены в самой аксиоматической системе невозможно доказать также и непротиворечивость системы. С этой точки зрения, не “измышляя гипотез”, т.е. не продлевая цепочку рассуждений за пределы наблюдаемого мира, вряд ли удастся непротиворечиво объяснить природу его важнейших сущностей – времени и пространства. Тем не менее, физика принципиально ограничивает круг рассматриваемых объектов и отношений явлениями наблюдаемого мира. Мысленный выход за пределы мира наблюдаемого – удел метафизики.

В-четвёртых, каждый из нас оказывается в роли упомянутого внешнего демона в тех случаях, когда объектом наблюдения является система, чьи состояния принципиально не могут быть соотнесены геометрически ни с каким объектом в окружающем пространстве. Примерами такой системы могут быть: абстрактный автомат, последовательность мыслей и т.п. И при этом мы утверждаем, что наблюдаемая система, в свою очередь, может включать демона (внутреннего), который, будучи включён в цепь её причинно-следственных связей, интерпретирует свой мир, так же как и мы свой в пространстве и во времени.

Здесь четвёртый тезис является ключевым. Он устанавливает индуктивное правило перехода от внутреннего наблюдателя к внешнему. Это правило оправдывает саму идею метафизического системного исследования, так как связывает наш повседневный опыт с предельным случаем его умозрительного обобщения – мысленным выходом за пределы наблюдаемого мира (как сказал Парменид “знают только сущее”).

Суть гипотезы состоит в том, что в отличие от ортодоксальных представлений о времени выдвигается предположение, о строгой линейной упорядоченности событий (отсутствии одновремённости) в системе любой природы, будь то система “наш мир” или какая-нибудь иная. Эта мысль является логическим следствием первого и второго тезисов. Действительно, если события линейно упорядочены, и их нельзя идентифицировать в пространстве, то одновремённые различные события невозможно наблюдать. Если бы такое было возможно, то различным одновремённым событиям следовало бы приписать различные точки в пространстве, а это исключается вторым тезисом.

Если в цепи последовательных событий могут быть выделены подцепи, соответствующие подсистемам наблюдаемого мира, то образ настоящего может включать множество псевдо-одновременных подсистем. Любые два события при этом не одновременны, но различные подцепи, чьи события, следуя друг за другом, “перемешаны” в одном отсеке времени, могут интерпретироваться автоматом - наблюдателем как одновременно существующие. Сказанное можно пояснить следующим примером. Всем известен способ кодирования сообщений, при котором в предъявленном тексте следует читать только вполне определённые символы, например каждый третий. Если текст представлен бесконечной последовательностью символов, то в нём можно передавать псевдо-одновременные сообщения, которые следует читать, скажем, через каждый второй, четвёртый и т.д. символы. При этом разные сообщения вплетаются в один фрагмент текста. В этом примере символами из некоторого алфавита обозначены различные состояния произвольной системы, в которых она оказывается, согласно выдвинутой гипотезе, в различные моменты времени.

Эта идея, несмотря на продолжительную драматическую предысторию, восходящую к Демокриту и Джордано Бруно, до сих пор не обрела заметного числа сподвижников в научных кругах.

Декларируя метафизический системный анализ как самостоятельное научное направление, необходимо, прежде всего, очертить “границы водораздела” со смежными науками. Таковыми здесь являются общая теория систем, с одной стороны, и физика (во всей совокупности своих направлений) с другой.

Общая теория систем ( Л. Берталанфи, А.Раппопорт, Н.Винер, Р.Эшби, М. Месарович, Я. Такахара и др.) изучает на междисциплинарном уровне наиболее общие свойства формальных отношений между абстрактными объектами. “Объектом исследований является не “физическая реальность”, не химическое или социальное явление (не субстанция), а “система”, т.е. формальная взаимосвязь между наблюдаемыми признаками и свойствами” [5]. Формально общая система определяется как отношение на непустых, абстрактных множествах.

Интересно сравнить это определение общей теории систем с определением метафизики Мартина Хайдеггера [1]: “Метафизика не специализированная наука, где мы с помощью некой умственной техники дознаёмся до чего-то в ограниченной предметной области. Мы воздержимся от того, чтобы помещать метафизику как научную дисциплину в ряду прочих. Нам придётся пока оставить открытым, что это вообще такое – метафизика. Мы видим только: метафизика есть фундаментальное событие в человеческом бытии. Её основные понятия суть понятия, последние же – как принято говорить в логике – суть пред-ставления, в которых мы представляем себе нечто общее или нечто вообще, нечто в аспекте того универсального, что многие вещи имеют между собою сообща.”(курсив и разрядка М. Хайдеггера).

Идея поставить во главу метафизики не частицу (субстанцию), а событие (время) была впервые предложена Уайтхедом. В его работе [6] эта мысль выражена с предельной ясностью: “Мы должны начать с события, приняв его за конечную единицу природного явления. Событие должно иметь отношение ко всему существующему, в том числе ко всем другим событиям”.

Пытаясь рассуждать о времени как о становлении, возникновении, инновации, процессе, мы всякий раз попадаем в кольцо противоречий. Потому что все эти понятия сами могут быть определены только по отношению ко времени, только с его помощью. Исследование законов движения в окружающем нас пространстве, предпринятое Эйнштейном, показало, что две системы находятся в относительном покое, если время для них течёт одинаково, и в относительном движении, если время для них течёт по-разному. Здесь несколько непривычно с точки зрения физических представлений расставлены акценты. Однако, таким образом, понятие относительного движения приобретает универсальный характер по отношению к любым (абстрактным) системам и сводится к определённым метрическим свойствам времени, проявляемым в различных системах по-разному. Различие собственных времён в разных системах выступает в качестве признака их относительного движения. Это очень важный результат, но он важен для понимания сущности движения, а не времени.

1. линейная упорядоченность событий является следствием физических законов, отражающих отношение объектов наблюдаемого мира;
2. физические законы являются следствиями линейной упорядоченности событий.

Среди известных концепций времени основными являются субстанциальная и реляционная. Первая предполагает наличие некоторого материального носителя времени. Вторая представляет собой попытку объяснить сущность времени или отдельные его свойства, исходя из суммы знаний о сущности взаимодействий (отношений) материальных объектов в физическом мире. Иными словами, в отношении ко времени предполагается первичность материального мира, обладающего изначальным свойством протяжённости в пространстве, не зависимым от времени.

Ни одна из попыток объяснить феномен времени во всей полноте его известных проявлений как следствие взаимодействий вещества и поля в пространстве не удалась. Поэтому всё больший интерес вызывает второй подход к концепции времени. Так, например, А.Н. Уайтхед в цитированной выше работе высказывает следующую мысль: “Пространство-время является спецификацией некоторых общих характеристик событий и их взаимной упорядоченности”. [6]

В своём известном мемуаре “О математических понятиях материального мира” он высказывается ещё более определённо в том смысле, что идеалом было бы сформулировать такие аксиомы монистической концепции универсума, из которых могли бы “с чрезвычайной простотой” вытекать все законы электромагнетизма и гравитации. При этом он считал, что беда естественнонаучных концепций в том, что их законы “предполагают геометрию” а должны были бы “создавать её” [6].

Необходимость смены научной парадигмы среди учёных, исследующих физические принципы устройства окружающего мира, по-видимому, впервые была осознана и провозглашена И. Пригожиным [7]. По его мнению необратимость (термодинамическая) не может быть выведена из законов взаимодействия материальных объектов. Необходимо заново пересмотреть эти законы, исходя из признания необратимости в качестве исходного постулата.

Результаты исследования собственных миров динамических систем [8] , проведенного автором настоящей работы, позволяют значительно усилить это предложение.

Линейная упорядоченность событий (время) произвольной (общей) системы не следствие, а первопричина геометрических и физических отношений между её подсистемами, отражающих статистические закономерности распределения состояний в цепи событий. Как показано там же, собственным наблюдателем общей системы может быть любая её подсистема, организованная как абстрактный односторонний автомат, выполняющий простейшую функцию – счёт и сортировку событий. Протяжённость собственного пространства системы такой наблюдатель определяет количеством состояний, отделяющих одно событие от другого.

Можно сказать, что конструктивная теоретико-системная концепция времени является центральной проблемой метафизики сегодня. Попытаемся, по крайней мере, наметить пути к её решению. При этом воспользуемся методом, который плодотворно используется в математической теории систем. Суть его состоит в следующем. Для того, чтобы дать формальное определение некоторой абстрактной системе, вначале, опираясь на интуицию, отбирают среди доступных наблюдению систем такие, которые примерно соответствуют мысленной конструкции. Затем анализируют отобранные реальные системы и создают формальную математическую модель, наделяя её такими абстрактными свойствами, которые обобщают свойства не только наблюдаемых, но и всех мыслимых аналогичных систем.

МАТЕМАТИЧЕСКИЕ ЧАСЫ – МОДЕЛЬ СИСТЕМЫ ВРЕМЕНИ

В своей знаменитой “Кибернетике” Н.Винер, проводя сравнительный анализ ньютоновского и бергсоновского времени, среди известных моделей реальности особым образом выделяет часовой автомат. Противопоставляя динамическое мышление Лейбница геометрическому мышлению Спинозы, он, в частности, замечает: “Итак, Лейбниц рассматривает мир автоматов, который, как и полагается ученику Гюйгенса, он строит по образцу часового механизма.”[9].

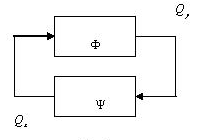
В качестве прообраза глобальной системы времени рассмотрим известную всем систему – часы. Если абстрагироваться от различных конструкций часов и воспользоваться кибернетическими представлениями, то систему математические часы можно рассматривать как два “чёрных ящика”, объединённых в систему так, что вход первого является выходом второго, вход которого, в свою очередь, является выходом первого (см. рисунок 1).

Таково устройство любого осциллятора, от песочных часов до электронных мультивибраторов.

Рассмотрим более подробно несколько характерных примеров.

Электронный мультивибратор. В очень упрощённом представлении он состоит из триггера и конденсатора . Множество событий можно рассматривать как объединение двух подмножеств: - заряд конденсатора достиг определённой величины и - переключение триггера в противоположное состояние. Событие “переключение триггера в противоположное состояние” является следствием события “заряд конденсатора достиг определённой величины”. Событие “заряд конденсатора достиг определённой величины” является следствием события “переключение триггера в противоположное состояние” и т.д.

Совершенно аналогично описывается процесс в маятниковых часах. Надо только заменить конденсатор маятником, заряд конденсатора отклонением маятника, триггер заменить храповиком, а переключение триггера - изменением положения храповика.

Песочные часы. Событие “песчинка упала в нижнюю часть конуса” является следствием события “песчинка находится в горловине конуса”. Событие “песчинка находится в горловине конуса” является следствием события “песчинка упала в нижнюю часть конуса” ( см. рис.2) и т.д.

(Для упрощения примера предполагается, что через горловину конуса проходит только одна песчинка). Как видите, здесь ход часов также обусловлен совместным действием прямой и обратной причинно – следственных связей. При этом “переворачивать” часы не требуется, если песчинок много.

Рис.2

Атомные часы. Событие “деление ядра атома” является следствием события “возникновение частицы, способной при взаимодействии с ядром вызвать его деление”. Событие “возникновение частицы, способной при взаимодействии с ядром вызвать его деление” является следствием события “деление ядра атома” и т.д.

Во всех этих примерах общим является то, что причинно – следственные связи образуют цикл на множествах причин и следствий, индуцирующий последовательность причинно – связанных событий. При этом сами события не эквивалентны, их можно сосчитать, они различаются по каким-то признакам (состояниям). И даже в тех случаях, когда состояния не различимы, события отличаются друг от друга как причины и следствия, что, собственно, и воспринимается нами как течение времени. Подобные циклы широко используются в различных автоматах именно с этой целью – упорядочить события. На рисунке 3 показан не очень серьёзный пример программного цикла.

С точки зрения внешнего демона, наблюдающего этот процесс, каждый оператор программного цикла может выполняться за секунду или за тысячу лет, но для внутреннего демона, чьё множество событий исчерпывается лишь теми, которые порождает оператор 1, каждое такое событие осуществляется в ускользающем моменте его собственного настоящего.

Если наблюдатель ощущает, что два следующие непосредственно друг за другом события разделены некоторым промежутком времени, то лишь благодаря тому, что он воспринимает и другие события, заполняющие этот промежуток. Если бы между двумя фиксированными событиями других событий не было, то непосредственно измерить, соответствующий им промежуток времени было бы невозможно. Но если время это линейная последовательность событий, значит должна существовать система, которая

её производит вследствие особенностей своей конструкции. С точки зрения выдвигаемой концепции эта особенность – причинно-следственный цикл, индуцирующий цепь событий, обобщающий те циклы, которые реализуются в часах различных конструкций и автоматах.

Когда мы говорим о часах как о приборе, моделирующем течение времени в наблюдаемом мире, то учитываем, что механизм его внутренних причинно – следственных связей (композиция функций и ) обусловлен физическими законами этого мира и замыслом конструктора. Обобщая понятие “часы” до уровня абстракции системы времени, мы, образно говоря, оказываемся внутри некоторой гиперсистемы “математические часы” такой, что любая система наблюдаемого мира является её подсистемой.

Анализируя систему математические часы, мы обнаруживаем, что цепь событий возникает вследствие упорядочивания замкнутой системой собственной области определения. Наиболее очевидными примерами таких систем могут служить компьютерные программы, автоматы, различные динамические системы, описываемые однородными дифференциальными или конечно – разностными уравнениями. Но все эти системы мы наблюдаем во времени лишь постольку, поскольку сами вместе с ними включены во всеобщую (для нашего мира) цепь событий. Следовательно, можно предположить, что все закономерности эволюции подобных систем являются следствием общих закономерностей, присущих той системе, частью которой они являются.

В работе автора [8] показано, что законы динамики материальной точки в трёхмерном пространстве являются выражением статистических закономерностей распределения состояний в цепи событий. Но там же показано, что знания законов движения абсолютно всех частиц в собственном мире системы недостаточно для восстановления последовательности состояний в цепи событий. Следовательно, линейный порядок цепи событий абстрактной динамической системы не выводится из законов движения материальных тел в её собственном мире.

1. Система времени это отношение на абстрактном бесконечном множестве , заданное биекцией , таким образом, что при любом разбиении множества на два непустых подмножества одно из них отображается в другое.

2. Для любого элемента множества имеются прообраз и образ, принадлежащие этому же множеству.

3. Отображение антисимметрично и антирефлексивно:

Первая и вторая аксиомы постулируют отсутствие начала и конца (бесконечность) времени, и определяют в качестве источника временных отношений связное отображение множества событий в себя (цикл причинно – следственных связей). Третья аксиома устанавливает специфические свойства бинарного отношения, по которым его следует относить к причинно – следственным связям. Биективность отображения, постулируемая первой аксиомой является следствием первого и второго тезисов исходной гипотезы системы времени.

На множестве для двух любых элементов и введём отношение порядка (следования) такое, что

. (1)

Иными словами, согласно данному определению, элемент следует после в том и только в том случае, если имеется непрерывная цепочка отображений, начинающаяся с элемента (прообраза) и заканчивающаяся элементом (образом). Элементы области определения системы времени будем называть событиями. Запись читается следующим образом: событие (старшее) предшествует (меньше) событию (младшему).

Теорема 1. Множество Q , упорядоченное отношением следования h является цепью событий системы времени.

Доказательство. Зафиксируем два произвольных элемента и множества . Вследствие аксиомы 2 имеем:

(2)

Обозначим . Согласно определению (4) каждое из этих подмножеств является цепью. При этом цепь не имеет наибольшего младшего элемента, а цепь - наименьшего старшего, так как в противном случае, либо множество событий конечно, что противоречит аксиоме 1, либо не выполняется аксиома 2. Допустим, что область пересечения этих подмножеств пуста. Тогда, вопреки утверждаемому в теореме, в соответствии с определением (4), выбранные элементы не сравнимы. Однако, при таком предположении отображение имеет две несвязные по отображению области определения, не совпадающие по отдельности с множеством , что противоречит аксиоме 1. Следовательно, множество пересечения цепей и не пусто. Но тогда вследствие биективности отображения , утверждаемого аксиомой 1, это множество может быть только цепью . А значит, произвольно выбранные элементы и множества сравнимы, что и требовалось доказать.

Теорема 2. Цепь событий является строго упорядоченным множеством.

Для того, чтобы отношение оказалось строгим порядком, необходимо и достаточно, чтобы оно было транзитивным, антирефлексивным (т.е. не имеет места ни при каком ) и сильно антисимметричным (т.е. ни для каких и соотношения и не могут выполняться одновременно).

Доказательство. 1.Транзитивность. Пусть имеются три события такие, что и . По определению (4) имеется непрерывная цепочка отображений от прообраза к образу и от прообраза к образу . Следовательно, имеется непрерывная цепочка отображений от к (), что и требовалось доказать.

2. Антирефлексивность и антисимметричность. Аксиома 3 даёт лишь необходимые, но не достаточные условия антирефлексивности и антисимметричности отношения . Это видно уже из простейшего примера. Пусть . Аксиома 3 не нарушена, но отношение порядка рефлексивно и симметрично, т.е. является отношением эквивалентности (см. рис. 4)

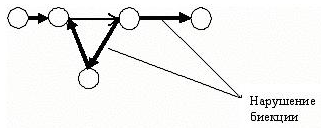
Однако, согласно аксиомам 1, 2 и теореме 1 множество - это одна бесконечная цепь событий. Следовательно, ни один из её конечных интервалов не может включать такого события, которое было бы отображено в предшествующее ему событие, так как при этом, либо цепь конечна, либо отображение не однозначно (см. рис. 5)

Множество событий не может представлять собой один конечный цикл, так как при этом нарушается требование бесконечности множества , и оно не может включать в качестве подмножества конечный или бесконечный цикл, так как при этом не выполняется требование биективности отображения, заданного на множестве (см. рис.5). Кроме того, множество событий не может состоять из циклов или иных подмножеств, не отображённых ( рис.4) друг в друга, так как это противоречит требованию аксиомы 1. Следовательно, система времени вообще не содержит конечных циклов.

И всё же, если в цепи имеется бесконечный замкнутый интервал, то рефлексивность и симметричность не противоречат аксиомам системы времени, так как в этом случае всё множество событий может представлять собой один бесконечный цикл.

Доказательство леммы. Во-первых, уточним, что мы имеем в виду, когда говорим о бесконечной цепи событий, каждый замкнутый интервал которой конечен. Для этого рассмотрим некоторый конечный интервал, включающий событий. Согласно аксиоме 2 прообраз наибольшего старшего и образ наименьшего младшего события также принадлежат цепи событий. Следовательно, имеем второй интервал, включающий первый и, соответственно событий. Поступая аналогичным образом, получим бесконечную последовательность интервалов, мощность которых бесконечно возрастает. Однако каждый из интервалов этой последовательности включает конечное число событий. Вопрос, следовательно, заключается в том, может ли замкнутый интервал, обозначенный конкретными событиями, например, и иметь дедекиндово сечение или щель. Так как только в этих случаях он является бесконечным интервалом. Предположим, что дело обстоит именно так. Обозначим и соответственно нижний и верхний классы дедекиндова сечения интервала . Обозначим наибольшее событие в нижнем классе. Согласно теореме 1 в верхнем классе должен иметься его образ , такой, что . Однако по определению дедекиндова сечения в верхнем классе отсутствует наименьшее событие, если в нижнем классе имеется наибольшее. А это значит, что любое событие из классаявляется образом события из этого же класса. Но так как - биекция, то одно и то же событие не может быть образом двух разных событий из верхнего и нижнего классов. Следовательно, наибольшее событие в нижнем классе дедекиндова сечения не имеет соответствующего образа в верхнем классе. Но в таком случае события и не сравнимы, что противоречит условию леммы, по которому - цепь. Подобные рассуждения могут быть проведены для иной разновидности дедекиндова сечения, при котором в верхнем классе имеется наименьшее событие, а в нижнем отсутствует наибольшее. Различие состоит лишь в том, что в этом случае мы приходим к противоречию с условием леммы по той причине, что невозможно найти в нижнем классе прообраз наименьшего события из верхнего класса. По отношению к щели аналогичная схема рассуждений приводит к противоречию с условием леммы по той причине, что в нижнем и верхнем классах сечения невозможно найти двух взаимно отображённых событий. Следовательно, лемма доказана, а значит доказана и теорема 2.

По аналогии с началами термодинамики вторая теорема может быть выражена в запретительной форме. А именно, ею устанавливается запрет на возможность существования машины времени как подсистемы, нарушающей порядок причинно – следственных связей.

И. Бродский. “Колыбельная трескового мыса”

При попытке исключить какую-либо из аксиом доказательство этих теорем становится невозможным. Следовательно, аксиомы необходимы для того, чтобы время обладало указанными свойствами. С другой стороны, ими определяется не время как таковое, а некоторая общая система, обладающая свойством индуцировать время. Важно также то, что наша модель улавливает одно из наиболее интригующих свойств времени, которое состоит в том, что достаточно указать на существование какого-либо события, как из этого следует существование нового события, а указанное уже является прошлым и так далее до бесконечности.

(3)

Кстати сказать, это свойство времени до сих пор (?) никак в точных науках не обозначено (слово “бренность”, мне кажется, имеет излишне эмоциональную окраску). Может быть, назвать его – транзиторность от английского слова transitory – преходящий?

Согласно второму тезису исходной метафизической гипотезы состояния системы времени являются внепространственной абстракцией для внешнего наблюдателя. Это значит, что они никаким способом не могут быть сопоставлены с результатами измерений длин отрезков и интервалов времени в его мире. Для того чтобы обобщить некоторую реально наблюдаемую систему до уровня абстракции системы времени необходимо “забыть” о связи чисел, отображающих её состояние, с результатами измерений пространства и времени. Но в таком случае значения, приписываемые состояниям системы времени, не могут быть соотнесены друг с другом из-за отсутствия общего для них базиса измерения. А это значит, что они не измеримы тем способом, которым мы обычно пользуемся, т.е. сопоставлением с системой базисных векторов пространства.

Пытаясь перейти от внешнего наблюдения некоторой абстрактной системы к внутреннему, мы ощущаем эту проблему с особой остротой. Действительно, не делая допущения о том, что множество внутренних наблюдателей обладает каким-то априорным, одинаковым для всех, знанием размерности и геометрических характеристик собственного пространства состояний, трудно вообразить, как они их измеряют. Однако в своём собственном мире мы умеем измерять состояния, наблюдаемых систем. Следовательно, можно предположить, что существует некоторый универсальный способ сравнения состояний абстрактной системы времени, не зависящий от выбора наблюдателя и гарантирующий сопоставимость результатов различных измерений. Отказываясь от этого предположения, мы автоматически признаем, что наше знание об окружающем мире вложено в нас извне, или является проявлением уникальной особенности наблюдателя, выделяющей его из иных подсистем системы времени. С нашей точки зрения такая позиция страдает неоправданной тоталитарностью. Предлагается гораздо более демократичная парадигма – рассматривать наш мир (т.е. абсолютно все объекты, объединённые общим пространством) всего лишь как некий образ одной из бесконечного множества систем, обладающей лишь теми свойствами, которые обусловлены строгой линейной упорядоченностью цепи событий.

Произвольное событие в системе теперь можно записать в виде , где индекс в скобках указывает время события (первый порядок), а нижний индекс- состояние системы (второй порядок различия). Более высокие порядки различия событий обусловлены их распределением по вложенным цепям событий подсистем, населяющих собственный мир системы времени. Пример фрагмента цепи событий системы времени, включающей множество подсистем, показан на рисунке 6.

Здесь кружками обозначена цепь событий подсистемы b, прямоугольниками – цепь событий подсистемы a. Индексами обозначены состояния системы времени.

Различие и тождество состояний, а также распределение событий между подсистемами, т.е. структуру, будем относить к абсолютным (объективным) признакам системы в том смысле, что и внутренний и внешний наблюдатели адекватно судят о тождестве и различии состояний. Если некоторое подмножество цепи событий является областью подсистемы для внутреннего наблюдателя, то это же подмножество воспринимается как область соответствующей подсистемы и внешним наблюдателем. При этом интерпретируется структура системы каждым наблюдателем по своему. Из собственного опыта нам известно, что внутренний наблюдатель интерпретирует её в образе объектов, взаимодействующих в пространстве и объектов, порождаемых этим взаимодействием. С другой стороны, согласно четвёртому тезису, принятой нами метафизической гипотезы, внешний наблюдатель интерпретирует эту же систему как внепространственную цепь событий, порождаемую эволюцией некоторой системы из своего (внешнего) мира. Нечто подобное имеет место, когда мы сталкиваемся с проблемой расшифровки текста, представленного неизвестными нам символами. Приходится допускать, что исследователь и создатель текста адекватны в оценке различия и тождества символов. Субъективности содержания сообщения, закодированного в цепи событий, противостоит объективность его структуры. Это положение, выдвигаемой метафизической гипотезы, отражает нашу веру в объективность универсума, основанную на опыте сопоставления множества индивидуальных восприятий окружающего мира различными наблюдателями.

Рассматривая цепь, где за каждым осуществлённым событием следует новое событие, характеризуемое определённым состоянием, причинно связанным с другими состояниями этой цепи, невозможно не обратить внимания на аналогию с односторонним ленточным автоматом. При этом можно предположить, что среди бесконечного множества событий такой цепи найдутся подмножества, которые обычно возникают вследствие целенаправленного поведения соответствующих автоматов. Подсистемы – автоматы обладают неким общим свойством. Оно состоит в том, что распределение состояний на некоторых интервалах цепи событий является функцией распределения состояний на предшествующих интервалах. Это свойство в теории автоматов называют памятью. Однако это же свойство определяет автомат как наблюдателя цепи событий, т.е. внутреннего наблюдателя системы времени.

М. Л. Цетлин [10], исследуя целесообразное поведение автомата, взаимодействующего со случайной средой, обратил внимание на один интересный аспект этой задачи. Для того чтобы максимизировать некоторую целевую функцию поведения (свой выигрыш) такой автомат должен вести счёт повторений одинаковых состояний (реакций) наблюдаемой им среды. Для автомата “вести счёт” означает совершать переходы из одного состояния в другое после определённого количества повторений одинаковых реакций среды. Следовательно, для достижения целесообразности собственного поведения наблюдатель должен отличать состояния друг от друга не только качественно, но и количественно, т.е. ведя счёт повторений каждого из состояний, наблюдаемой системы.

С помощью этой несложной процедуры абстрактный внутренний наблюдатель (подсистема – автомат), движимый необходимостью осуществлять целесообразное поведение (например, для выживания), имеет возможность воспринимать собственный мир системы времени так же, как мы воспринимаем свой мир – в пространстве и во времени. При этом единственным необходимым условием измеримости пространства и времени является счётность цепи событий. Но в соответствии с доказанной леммой цепь событий дискретна, а значит и счётна.

ЗАКЛЮЧЕНИЕ

Одной из самых сложных проблем философии, с момента её зарождения до наших дней является проблема отношения бытия ко времени. Вот, что по этому поводу писал Мартин Хайдеггер: “Между тем от метафизики на протяжении её истории от Анаксимандра до Ницше истина бытия остаётся скрытой”[12]

“Бытие никак не вещь, соответственно оно не нечто временное, тем не менее, в качестве присутствования оно всё равно определяется временем. Время никак не вещь, соответственно оно не нечто сущее, но остаётся в своём протекании постоянным, само, не будучи ничем временным наподобие существующего во времени. Бытие и время взаимно определяют друг друга, однако так, что ни первое – бытие – нельзя рассматривать как временное, ни второе – время – как сущее. Обдумывая всё это, мы гоняем по кругу взаимопротиворечащих высказываний.” [13]. Общепринятую точку зрения на проблему отношения бытия ко времени, Уайтхед выразил значительно определённее и короче: “событие имеет современников” [6]. Имеется в виду, что настоящее есть множество одновременных событий. Хотя каждый из нас, опираясь на собственный опыт, готов присоединиться к этой точке зрения, философия и естественные науки до сих пор “гоняют по кругу взаимопротиворечащих высказываний”. В чём здесь дело?

В концепции системы времени эти проблемы получают неожиданное разрешение. Бытия, в смысле присутствия всего сущего, в каждый момент настоящего в системе времени нет, но можно говорить об одновременной эволюции (бытии) всех доступных наблюдению подсистем в одном отсеке времени (прошлого). Действительно, с точки зрения концепции системы времени нет ничего загадочного в том, что достаточно длинная цепь событий, отображённая в памяти автомата – наблюдателя, может интерпретироваться как ансамбль цепей событий “одновременно” эволюционирующих подсистем. Пример совместного бытия подсистем в одном отсеке времени показан на рисунке 6. Отдельно взятое событие не может быть содержательно интерпретировано или измерено. Только последовательность событий, отображённая в памяти наблюдателя, может для него что-то означать. Следовательно, любой образ окружающего мира является образом его прошлого. Настоящего, населённого множеством объектов, в системе времени не существует вовсе. В известной концепции времени Бергсона отсутствует будущее. В предлагаемой концепции системы времени исключается не только будущее, но и настоящее. Точнее говоря, настоящее присутствует только в качестве отдельно взятого события, с помощью которого автомат – наблюдатель идентифицирует предшествующую последовательность событий [11].

С точки зрения теории собственных миров системы времени [8] материальная точка, как динамический объект в пространстве, является лишь частным образом динамической подсистемы. Её траектория полностью определяется распределением количеств состояний в цепи событий. Но знания распределения количеств состояний не достаточно для детального восстановления порядка их следования. Требуется ещё понятие информационного взаимодействия, так как последовательности событий определяются не только взаимным расположением подсистем в пространстве, т.е. распределением вероятностей состояний в цепи событий, но и порядком чередования состояний (сообщениями), соответствующими этим последовательностям. Сказанное поясняет следующий пример. Пусть для внешнего наблюдателя система времени это последовательность символов, которую он интерпретирует как текст. Всё, что можно сказать о поведении её подсистем в пространстве собственного мира, заключено в распределении относительных количеств (вероятностей) символов текста. Однако для прочтения самого текста этого не достаточно. Следовательно, всё сущее в собственном мире системы времени характеризуется не только параметрами, связанными с пространством и временем (координатами, импульсами, энергией, и т. п.), но и чем-то иным, что можно сравнить с сознанием, так как оно определяет информационную значимость сущего. Идея изначального присутствия сознания в сущем “дублирование материи сознанием” является основой эволюционистской концепции Т. де Шардена. Эта идея является неотъемлемой частью органистической метафизики Уайтхеда, и вообще монистического направления в философии. В концепции системы времени эта идея получает математическое обоснование.

Концепция системы времени существенно раздвигает границы принципа относительности. Такие незыблемые абсолюты как материя, поле, субстанция низводятся до относительных понятий, зависящих от выбора наблюдателя. То, что для внутреннего наблюдателя развёртывается в виде драматической истории материальных взаимодействий, для внешнего наблюдателя может быть чем угодно – игрой воображения, компьютерной программой и т. п. В связи с этим возникают новые и возрождаются старые гуманитарные проблемы философии. Когда мы говорим о том, что наш мир

1. Хайдеггер М. Основные понятия метафизики, в сб.: Время и бытие: Статьи и выступления: Пер. с нем. – М.: Республика, 1993. с.: 327 – 345.
2. Turchin, Valentin; Heylighen, Francis; and Joslyn, Cliff: (1992) 1992 \pc\ Nodes, \pc\ Tech Report.
3. Turchin, Valentin: (1993) "Cybernetic Ontology of Action", Kybernetes, v. 22:2,

pp.10-31,

4. Turchin, Valentin: (1991) "Cybernetic Metaphysics", \pc\ Technical Report,
5. М. Месарович, Я. Такахара. Общая теория систем. Математические основы.- М.: Мир, 1978. 311с.
6. Уайтхед А. Наука и современный мир, в сб.: Избранные работы по философии: Пер. с англ. – М.: Прогресс, 1990. с.: 56 – 272.
7. И. Пригожин. От существующего к возникающему: Время и сложность в физических науках. – М.: Наука, 1985. 327с.
8. А. Заславский. Собственные миры динамических систем.
9. Норберт Винер. Кибернетика, или управление и связь в животном и машине. – М.: Советское радио, 1958. 213с.
10. М. Л. Цетлин. Исследования по теории автоматов и моделированию биологических систем. – М.: Наука, 1969. 316с.
11. Брауэр В. Введение в теорию конечных автоматов: Пер. с нем. – М.: Радио и связь, 1987. – 392с.
12. Хайдеггер М. Введение к: “Что такое метафизика?”, в сб.: Время и бытие: Статьи и выступления: Пер. с нем. – М.: Республика, 1993. с.: 27 – 36.
13. Хайдеггер М. Время и бытие, в сб. Время и бытие: Статьи и выступления:: Пер. с нем. – М.: Республика, 1993. с.: 391 – 407.

В работе изложены философские и теоретико-системные принципы метафизической концепции системы времени, опирающейся на идею существования собственных миров абстрактных систем. Сформулированы аксиомы системы времени. Показано, что измеримость пространства и времени непосредственно связана со счётностью цепи событий. Доказана дискретность цепи событий системы времени.