© А.М.Заславский
ГЕОМЕТРИЧЕСКИЙ ОБРАЗ ВНУТРЕННЕГО МИРА АБСТРАКТНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
(ИНТРОСПЕКТИВНЫЙ АНАЛИЗ И СИНТЕЗ ВРЕМЕННЫХ РЯДОВ)
А. М. Заславский
![]()
АННОТАЦИЯ
Обсуждается гипотеза о строгой линейной упорядоченности событий (гипотеза неодновременности) в системе “наш мир”. Согласно предложенной гипотезе содержательный образ наблюдаемого мира в данный момент времени определяется не множеством одновременных событий, а последовательностью его состояний, предшествующих этому моменту. В отличие от общепринятой гипотезы одновременности, следуя которой можно лишь постулировать геометрические свойства пространства событий, данная гипотеза открывает возможность дедуктивного вывода этих свойств. Исследуется внутренняя геометрия многомерного собственного пространства – времени абстрактной динамической системы, все состояния которой линейно упорядочены (не одновременны) относительно внешнего наблюдателя. Доказывается, что линейные преобразования этого пространства – времени при изменении системы отсчёта являются преобразованиями Лоренца со всеми, вытекающими отсюда, следствиями специальной теории относительности. На основании этих исследований предложен новый метод (интроспективный) анализа и синтеза временных рядов. Интроспективный анализ позволяет по известному распределению значений временного ряда построить геометрическую релятивистскую модель, порождающей его, динамической системы в её собственном многомерном пространстве – времени. Интроспективный синтез позволяет по известному ансамблю траекторий динамической системы в её собственном многомерном пространстве найти распределение значений соответствующего ей временного ряда.
ВВЕДЕНИЕ
Общепринятая модель процесса эволюции сложной системы (в качестве которой можно рассматривать весь доступный наблюдению мир) опирается на гипотезу одновременности событий. Суть этой гипотезы в том, что каждому моменту времени системы ставится в соответствие множество одновремённых состояний множества её подсистем. Этим предположением фактически постулируется наличие пространства, в котором отображается эволюция системы, в качестве вместилища её одновремённых состояний. Классическая физика приписывала одновремённости абсолютный характер. В теории относительности одновремённость пространственно разделённых событий уже не абсолютна, но по-прежнему принимается в качестве концептуального базиса физического пространства.
Недостаток этой модели в том, что она требует от реального наблюдателя, фиксирующего события по сигналам, поступающим от наблюдаемого процесса, сверхъестественной способности мгновенно распознавать одновременные состояния множества одновременно наблюдаемых подсистем. Когда в теории относительности утверждается одновременность каких-либо событий, это означает признание именно такой способности наблюдателя, предполагающей бесконечно большую скорость преобразования информации, а, следовательно, и распространения сигналов (если, конечно, не допускать возможности наблюдателя бесконечно малых размеров). Противоречие с основным постулатом теории очевидно.
Модель процесса эволюции сложной системы, предложенная в концепции системы времени [1,2], напротив, основана на отрицании одновремённости состояний. Система времени представляет собой такую динамическую систему, в которой каждое состояние каждой из её подсистем осуществляется не одновременно с другими состояниями так, что множество состояний системы оказывается линейно упорядочено в цепи событий. Образ настоящего в такой системе определяется распределением последовательных состояний в цепи событий, предшествующей текущему моменту времени. Предположение о применимости подобной модели к системе “наш мир” также, всего лишь гипотеза, которую невозможно подтвердить или опровергнуть непосредственным наблюдением или экспериментом. Однако, в отличие от гипотезы одновременности, принимая которую, можно лишь постулировать геометрические свойства пространства событий, данная гипотеза открывает возможность дедуктивного вывода этих свойств. Это, в свою очередь, означает возможность дедуктивного вывода законов взаимодействия подсистем в системе времени.
Идея данного исследования схематично и неполно изложена в [2]. Настоящая работа задумывалась, как попытка раскрыть эту идею с большей полнотой и строгостью математических выкладок. Однако в ходе анализа следствий из гипотезы неодновременности были получены также принципиально новые результаты.
КИБЕРНЕТИЧЕСКАЯ МОДЕЛЬ НАБЛЮДАТЕЛЯ В СИСТЕМЕ ВРЕМЕНИ
Любая физическая теория начинается с определения наблюдателя и/или его свойств. Это связано с тем, что как показывает опыт, законы природы в общем случае не инвариантны к замене одного наблюдателя другим. В теориях, опирающихся на гипотезу одновремённости, наблюдатель представляет собой сложную систему, манипулирующую специальными твёрдыми телами (мерными линейками), обладающую возможностью мгновенно распознавать одновременные состояния и измерять промежутки времени между событиями.
В системе времени с её абстрактными линейно упорядоченными состояниями, где пространство изначально не задано, ни о каких мерных линейках, естественно, не может быть и речи. Следовательно, прежде чем приступать к исследованию следствий гипотезы неодновременности, необходимо дать определение наблюдателя как системы, отображающей изменения состояний наблюдаемой системы времени в пространстве.
Будем различать внешнего и внутреннего наблюдателей. Конструкция внешнего наблюдателя не может быть определена в терминах наблюдаемой им системы. Собственно гипотеза системы времени есть ни что иное, как гипотетический образ абстрактной динамической системы, создаваемый её внешним наблюдателем. С точки зрения внешнего наблюдателя система времени проявляет себя в виде цепи событий, отображённой в его памяти. В качестве исходного постулата принимается такое направление “стрелы времени”, которому соответствует положительное приращение количества событий в любой системе. Это значит, что цепь событий, начиная с некоторого начального события, в определённые дискретные моменты времени ![]() по часам внешнего наблюдателя увеличивается каждый раз на одно событие.
по часам внешнего наблюдателя увеличивается каждый раз на одно событие.
Событие в системе времени будем обозначать переменной ![]() , принимающей в каждый момент времени одно из
, принимающей в каждый момент времени одно из ![]() различных значений
различных значений ![]() , соответствующих
, соответствующих ![]() возможным состояниям системы. В разные моменты времени система может оказываться в одних и тех же состояниях. В общем случае цепь событий состоит из повторяющихся состояний.
возможным состояниям системы. В разные моменты времени система может оказываться в одних и тех же состояниях. В общем случае цепь событий состоит из повторяющихся состояний.
Подсистемам системы времени соответствуют подцепи общей цепи событий (см. рис.1). Повторяющиеся состояния на рисунке обозначены одним цветом. Состояния одной и той же подсистемы на рисунке обозначены фигурами одной и той же формы.

Рис. 1
Обозначим количество подсистем в системе времени ![]() . Событие в
. Событие в ![]() - той подсистеме времени будем обозначать переменной
- той подсистеме времени будем обозначать переменной ![]() , принимающей в каждый момент времени
, принимающей в каждый момент времени ![]() одно из
одно из ![]() различных значений
различных значений ![]() , соответствующих
, соответствующих ![]() возможным состояниям
возможным состояниям ![]() - той подсистемы. Число
- той подсистемы. Число ![]() будем называть размерностью подсистемы. Понятно, что система может состоять из подсистем с разным количеством возможных состояний. Так что точнее следовало бы говорить об
будем называть размерностью подсистемы. Понятно, что система может состоять из подсистем с разным количеством возможных состояний. Так что точнее следовало бы говорить об ![]() возможных состояний
возможных состояний ![]() - той подсистемы. Однако для упрощения обозначений будем принимать это во внимание лишь в тех случаях, когда речь будет идти именно о подсистемах различной размерности.
- той подсистемы. Однако для упрощения обозначений будем принимать это во внимание лишь в тех случаях, когда речь будет идти именно о подсистемах различной размерности.
Особенность внешнего наблюдателя, по определению, состоит в том, что любая подсистема системы времени проявляет себя по отношению к нему также как и система в целом, а именно – в виде увеличивающейся цепи событий. Иными словами, внешний наблюдатель не связан ни с одной из подсистем системы времени так, чтобы её состояния воспринимались им как неизменные. Он воспринимает эволюцию системы времени как изменяющееся распределение состояний в цепи событий. Пусть система времени при переходе от события ![]() (состоящего в том, что в момент времени
(состоящего в том, что в момент времени ![]() она находится в состоянии
она находится в состоянии ![]() ) к событию
) к событию ![]() оказывается
оказывается ![]() раз в i-том состоянии
раз в i-том состоянии ![]() . Этот процесс можно рассматривать как повторение i-того состояния
. Этот процесс можно рассматривать как повторение i-того состояния ![]() раз, или как изменение i-того состояния на
раз, или как изменение i-того состояния на ![]() дискретных единиц. Таким образом, на отрезке времени
дискретных единиц. Таким образом, на отрезке времени ![]() относительно внешнего наблюдателя цепь событий характеризуется распределением приращений состояний
относительно внешнего наблюдателя цепь событий характеризуется распределением приращений состояний ![]() , где каждое приращение
, где каждое приращение ![]() . Для восприятия этого распределения не требуется базис, относительно которого производится отсчёт изменений, достаточно просуммировать повторяющиеся состояния. Следовательно, внешний наблюдатель отображает абсолютные изменения состояний системы времени. Более того, согласно выдвинутому в (1) принципу измерения состояний системы времени, распределение этих изменений не зависит от выбора наблюдателя, внешнего или внутреннего, отражая объективную структуру системы времени.
. Для восприятия этого распределения не требуется базис, относительно которого производится отсчёт изменений, достаточно просуммировать повторяющиеся состояния. Следовательно, внешний наблюдатель отображает абсолютные изменения состояний системы времени. Более того, согласно выдвинутому в (1) принципу измерения состояний системы времени, распределение этих изменений не зависит от выбора наблюдателя, внешнего или внутреннего, отражая объективную структуру системы времени.
В отличие от внешнего, внутренний наблюдатель является подсистемой системы времени и его конструкция требует определения.
Представим себе модель системы времени (с точки зрения внешнего наблюдателя) в виде множества односторонних ленточных автоматов (подсистем) А1, …Аk, … с одной общей бесконечной лентой. Лента разбита на ячейки, пронумерованные как моменты времени ![]() , и дважды проходит через каждый автомат, образуя петлю, как показано на рис. 2, взаимодействующую с автоматами двумя полуветвями.
, и дважды проходит через каждый автомат, образуя петлю, как показано на рис. 2, взаимодействующую с автоматами двумя полуветвями.

Рис. 2
В ячейках одной полуветви автоматы отмечают свои состояния ![]() (на рис. показано стрелками, направленными к ленте). С ячеек второй полуветви автоматы считывают свои состояния и состояния иных автоматов (стрелки направлены от ленты), соответствующие предшествующим моментам времени. Поведение автомата (выбор последующих состояний в зависимости от предыдущих) в общем случае определяется значениями функций его состояний
(на рис. показано стрелками, направленными к ленте). С ячеек второй полуветви автоматы считывают свои состояния и состояния иных автоматов (стрелки направлены от ленты), соответствующие предшествующим моментам времени. Поведение автомата (выбор последующих состояний в зависимости от предыдущих) в общем случае определяется значениями функций его состояний ![]() .
.
В контексте данной работы нас не интересует вопрос о том, как именно влияют функции состояний автоматов на их поведение – это проблема кибернетики, а не метафизики. Важно то, что такие функции существуют и отображают состояния системы времени в принципе. Так как множество состояний системы времени счётное [1], то, не снижая общности рассуждений, можно считать областью значений функций состояний множество целых чисел ![]() ,
,
Пусть в составе системы имеется автомат (обозначим его индексом ![]() ), такой конструкции, что относительно малые изменения функций его состояний
), такой конструкции, что относительно малые изменения функций его состояний ![]() линейны относительно малых приращений количеств повторяющихся состояний
линейны относительно малых приращений количеств повторяющихся состояний ![]() - той подсистемы и некоторой произвольной
- той подсистемы и некоторой произвольной ![]() - той подсистемы
- той подсистемы
![]() , (2)
, (2)
где в общем случае![]() ,
, ![]() .
.
Относительная малость приращений функций состояний данного автомата и количеств повторяющихся состояний ![]() - той и
- той и ![]() - той подсистем математически выражается отношениями
- той подсистем математически выражается отношениями
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (3)
. (3)
Поведение рассматриваемого автомата, определяемое функциями состояний (2), соответствует счёту количеств повторяющихся состояний в цепи событий системы времени. Подобный автомат, ведущий счёт повторяющихся состояний, будем называть внутренним (линейным) наблюдателем системы. При этом, ![]() - тую подсистему будем называть объектом наблюдения, а
- тую подсистему будем называть объектом наблюдения, а ![]() - тую подсистему – объектом начала отсчёта. Изменения функций состояний внутреннего наблюдателя отражают изменения состояний наблюдаемой подсистемы относительно изменений состояний подсистемы – объекта начала отсчёта.
- тую подсистему – объектом начала отсчёта. Изменения функций состояний внутреннего наблюдателя отражают изменения состояний наблюдаемой подсистемы относительно изменений состояний подсистемы – объекта начала отсчёта.
Принцип действия подобного автомата – наблюдателя может быть приближённо описан с помощью следующего простого алгоритма. Каждая ![]() - тая функция его состояния
- тая функция его состояния ![]() получает положительное приращение +1 после того как
получает положительное приращение +1 после того как ![]() - тое состояние наблюдаемой
- тое состояние наблюдаемой ![]() - той подсистемы повторится в цепи событий не менее чем
- той подсистемы повторится в цепи событий не менее чем ![]() раз, и отрицательное приращение –1 после того как
раз, и отрицательное приращение –1 после того как ![]() - тое состояние объекта начала отсчёта повторится в цепи событий не менее чем
- тое состояние объекта начала отсчёта повторится в цепи событий не менее чем ![]() раз. При этом отсчёт повторений состояний наблюдаемой подсистемы и объекта начала отсчёта возобновляется с нуля каждый раз после очередного изменения соответствующих функций состояний автомата – наблюдателя. Не трудно заметить, что для автомата, описанной выше конструкции, изменения целочисленных функций состояний
раз. При этом отсчёт повторений состояний наблюдаемой подсистемы и объекта начала отсчёта возобновляется с нуля каждый раз после очередного изменения соответствующих функций состояний автомата – наблюдателя. Не трудно заметить, что для автомата, описанной выше конструкции, изменения целочисленных функций состояний ![]() на отрезке времени
на отрезке времени ![]() тем точнее отвечают формуле (2), чем меньше погрешность округления правой части, т.е., чем больше относительные изменения
тем точнее отвечают формуле (2), чем меньше погрешность округления правой части, т.е., чем больше относительные изменения ![]() и
и ![]() количеств состояний.
количеств состояний.
В отношении внутренних наблюдателей системы времени будем руководствоваться гипотезой, согласно которой существует столь малый отрезок наблюдаемой цепи событий, на котором различимы состояния системы и поддаётся счёту количество их повторений, но не различим их порядок следования. Неразличимость порядка следования достаточно близких во времени событий характерна для уровня прототемпорального восприятия [3]. Известно, что для человека с его органами чувств периоды длительностью (20-50) ms могут вмещать события, которые поддаются счету, но их невозможно расположить в каком-то временном порядке. Следствием этой гипотезы является то, что последовательность состояний в цепи событий из-за неопределённости прототемпорального восприятия вообще не может быть предметом наблюдений. Наблюдатель с прототемпоральным порогом восприятия может анализировать лишь эволюцию плотностей распределения состояний в цепи событий. Именно вследствие неразличимости порядка следования близких во времени состояний внутреннему наблюдателю необходима идея пространства. При этом прототемпоральному промежутку цепи событий ставятся в соответствие: один момент времени, отношение на множестве плотностей распределения состояний, заполняющих промежуток, и отношение этого множества к моменту времени. Подобная идея не требуется внешнему наблюдателю, который, по определению, различает порядок следования всех без исключения состояний в наблюдаемой им цепи событий.
Вообще говоря, цепь событий системы времени может рассматриваться с разной степенью детализации, обусловленной разрешающей способностью наблюдателя. Наиболее детальное описание цепи событий получим, учитывая каждое событие, наименее детальное – рассматривая такие её участки, на которых абсолютные значения количеств повторяющихся состояний стремятся к бесконечности, а относительные к нулю. В последнем случае цепь событий будем называть псевдоконтинуальной. Строго континуальной цепи событий не может существовать ни при каких обстоятельствах вследствие доказанной в [1] леммы дискретности времени. Исследуя геометрический образ внутреннего мира системы времени, будем считать, что объектом наблюдения является именно псевдоконтинуальная цепь событий, так как лишь в этом предельном случае можно приближённо отображать эволюцию её подсистем траекториями в пространстве состояний, т.е. геометрически.
Рассмотрим основные принципы измерения времени наблюдателями системы. Так как событиями в системе являются её состояния, то сумма количеств всех состояний и есть количество событий ![]() . Для системы в целом вследствие линейности цепи событий имеем следующее очевидное равенство
. Для системы в целом вследствие линейности цепи событий имеем следующее очевидное равенство
![]() . (4)
. (4)
Так как множество событий любой из подсистем системы времени, являясь подмножеством общей цепи событий, также линейно упорядочено, то в отношении его справедливо аналогичное равенство
![]() . (5)
. (5)
Здесь ![]() - количество событий в наблюдаемой подсистеме.
- количество событий в наблюдаемой подсистеме.
Если для внешнего наблюдателя собственный датчик времени может не иметь с наблюдаемой им системой ничего общего, то для внутреннего наблюдателя датчиком времени может быть только счётчик событий одной из подсистем.
Это значит, что промежуток между двумя, следующими друг за другом, событиями наблюдаемой системы может быть заполнен для внешнего наблюдателя событиями, происходящими в других системах, а для внутреннего – лишь событиями, происходящими в его собственной системе. Так как, по определению, внутренний наблюдатель отображает изменения состояний множества наблюдаемых подсистем относительно одной подсистемы – объекта начала отсчёта, то логично использовать в качестве локального датчика времени счётчик событий именно этой подсистемы
![]() . (6)
. (6)
При этом отображение изменений состояний всех наблюдаемых подсистем осуществляется в одном времени.
Среди множества наблюдаемых подсистем могут оказаться такие (обозначим их индексом ![]() ), чьи состояния изменяются синхронно с состояниями объекта начала отсчёта
), чьи состояния изменяются синхронно с состояниями объекта начала отсчёта
![]() . (7)
. (7)
О таких подсистемах будем говорить, что они находятся в покое относительно наблюдателя, если ![]() .
.
ГЕОМЕТРИЧЕСКАЯ МОДЕЛЬ НАБЛЮДАТЕЛЯ
В теории относительности в качестве датчика собственного времени рассматриваются часы, покоящиеся, относительно наблюдателя. При этом ход часов считается заданным, хотя и не ясно с каким процессом он синхронизирован. Говоря о том, что ход часов должен быть синхронизирован с равномерно движущимся объектом, или периодическим процессом, мы замыкаем порочный логический круг, так как равномерность движения или периодичность процесса можно установить, лишь с помощью часов, ход которых мы пытаемся определить. Сам же покоящийся объект никак не проявляет себя в уравнениях движения относительно собственного наблюдателя. Для разрешения этого противоречия А. Эйнштейн предлагал понятие периодического процесса считать предшествующим понятию времени, так же как понятие твёрдого тела он считал предшествующим понятию пространства [4].
В этой и других подобных концепциях время и пространство заданы (a priori) в виде геометрической конструкции с заранее известными свойствами.
Напротив, принципиальным моментом предложенной модели является то, что понятие пространства в ней формирует наблюдатель на основании анализа распределения линейно упорядоченных состояний в цепи событий, (понятие времени предшествует понятию пространства). Здесь в качестве датчика времени используется одна из наблюдаемых подсистем – объект начала отсчёта, чьи состояния сравниваются наблюдателем с состояниями всех остальных наблюдаемых подсистем, а время измеряется количеством событий объекта начала отсчёта. Так как распределение состояний объекта начала отсчёта в цепи событий не зависит от выбора наблюдателя, формула (6) задаёт его объективное собственное время.
Для того чтобы дискретные функции состояний внутреннего наблюдателя отобразить в геометрическом пространстве и времени, поставим в соответствие паре смежных (следующих непосредственно друг за другом) событий объекта начала отсчёта квант времени ![]() , а минимальному изменению
, а минимальному изменению ![]() - той функции состояния
- той функции состояния ![]() квант расстояния
квант расстояния ![]() .
.
Эти величины будем считать универсальными постоянными, имеющими одинаковые значения для любых наблюдателей и не зависящими от выбора объекта начала отсчёта. Такое допущение оправдано стремлением исключить влияние произвольно выбранных масштабов измерений различных наблюдателей на результаты сравнения относительных геометрических характеристик эволюции различных подсистем.
Так как квант времени и квант расстояния – константы, то их отношение ![]() также является универсальной постоянной
также является универсальной постоянной ![]() .
.
Умножим правую и левую части уравнения (2) на ![]() и на коэффициент
и на коэффициент 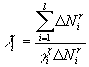 , (8)
, (8)
после чего получим
![]() . (9)
. (9)
Обозначим ![]() =
= ![]() - отображение в пространстве состояний внешнего наблюдателя абсолютного приращения
- отображение в пространстве состояний внешнего наблюдателя абсолютного приращения ![]() -того состояния
-того состояния ![]() - той подсистемы. Обозначим
- той подсистемы. Обозначим ![]() =
= ![]() - отображение в пространстве состояний внутреннего наблюдателя приращения
- отображение в пространстве состояний внутреннего наблюдателя приращения ![]() -того состояния
-того состояния ![]() - той подсистемы относительно
- той подсистемы относительно ![]() - того объекта начала отсчёта.
- того объекта начала отсчёта.
Учитывая (6), обозначим ![]() . Величина
. Величина ![]() представляет собой геометрический образ приращения собственного времени наблюдателя. С учётом введенных обозначений перепишем уравнения в виде
представляет собой геометрический образ приращения собственного времени наблюдателя. С учётом введенных обозначений перепишем уравнения в виде
![]() . (10)
. (10)
Выразим из этих уравнений абсолютные приращения состояний наблюдаемой подсистемы
![]() . (11)
. (11)
Суммируя правые и левые части этих равенств по всем индексам состояний, найдём
![]() , (12)
, (12)
где: ![]() ,
, ![]() .
.
Учитывая (5), обозначим ![]() . Величина
. Величина ![]() представляет собой геометрический образ приращения времени внешнего наблюдателя, измеренного количеством событий
представляет собой геометрический образ приращения времени внешнего наблюдателя, измеренного количеством событий ![]() - той подсистемы.
- той подсистемы.
Допуская псевдоконтинуальность цепи событий при геометрическом представлении системы времени, можно в пределе перейти от конечных разностей к дифференциалам.
![]() , (13)
, (13)
![]() . (14)
. (14)
Рассматривая формально пространство событий системы времени как ![]() - мерное многообразие, запишем эти уравнения в виде:
- мерное многообразие, запишем эти уравнения в виде:
![]() ,
, ![]() , (15)
, (15)
где обозначено: ![]() ,
, ![]() .
.
ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В СИСТЕМЕ ВРЕМЕНИ
Уравнения (15) устанавливают связь между результатами наблюдений внешнего и внутреннего наблюдателей за поведением ![]() - той подсистемы. Изменениям состояний поставлены в соответствие приращения осей координат. Изменениям времени также соотнесены числа, формально рассматриваемые как отрезки оси времени. При этом внутренний наблюдатель измеряет приращения состояний наблюдаемой им подсистемы относительно некоторой другой подсистемы – объекта начала отсчёта. Систему координат, в которой отображаются относительные изменения состояний наблюдаемых подсистем, и часы, измеряющие ход времени по количеству событий в подсистеме – объекте начала отсчёта, будем, как принято, называть системой отсчёта. Заметим, что преобразование системы отсчёта, связанное с переходом к другому объекту начала отсчёта, изменяя результаты наблюдения внутреннего наблюдателя, не влияет на результаты наблюдений внешнего.
- той подсистемы. Изменениям состояний поставлены в соответствие приращения осей координат. Изменениям времени также соотнесены числа, формально рассматриваемые как отрезки оси времени. При этом внутренний наблюдатель измеряет приращения состояний наблюдаемой им подсистемы относительно некоторой другой подсистемы – объекта начала отсчёта. Систему координат, в которой отображаются относительные изменения состояний наблюдаемых подсистем, и часы, измеряющие ход времени по количеству событий в подсистеме – объекте начала отсчёта, будем, как принято, называть системой отсчёта. Заметим, что преобразование системы отсчёта, связанное с переходом к другому объекту начала отсчёта, изменяя результаты наблюдения внутреннего наблюдателя, не влияет на результаты наблюдений внешнего.
Пусть имеются две системы отсчёта: одна, связанная с ![]() - той подсистемой, а вторая – с
- той подсистемой, а вторая – с ![]() - той. Записывая уравнения (15) в матричной форме для указанных объектов начала отсчёта, получим:
- той. Записывая уравнения (15) в матричной форме для указанных объектов начала отсчёта, получим:
![]()
![]() , (16)
, (16)
где обозначено: ![]() ,
, ![]()
![]() ,
, ![]() , индексы
, индексы ![]() ,
, ![]() пробегают значения от 0 до
пробегают значения от 0 до ![]() .
.
Из этой системы уравнений, линейных относительно малых приращений состояний и времени, найдём
![]() , (17)
, (17)
где ![]() .
.
Мы получили в общем виде формулы преобразования систем отсчёта внутреннего наблюдателя системы времени. Заметим сразу, что эти преобразования не Галилеевы так как при переходе от одного объекта начала отсчёта к другому изменяются не только приращения состояний наблюдаемой подсистемы, но и приращения времени. Коэффициенты преобразований ![]() могут быть определены лишь с помощью дополнительных величин – инвариантов преобразований. Такими инвариантами, например, определяющими группу преобразований Лоренца в специальной теории относительности, являются предельная скорость изменения состояний и квадратичная форма специального вида, получившая в теории относительности название “интервал в пространстве событий”.
могут быть определены лишь с помощью дополнительных величин – инвариантов преобразований. Такими инвариантами, например, определяющими группу преобразований Лоренца в специальной теории относительности, являются предельная скорость изменения состояний и квадратичная форма специального вида, получившая в теории относительности название “интервал в пространстве событий”.
Инвариантность предельной скорости постулируется в физике на основании обобщения известных экспериментов по измерению скорости распространения в пустоте электромагнитных волн.
Инвариантность интервала принимается без доказательств на том основании, “…что иначе мы пришли бы к физически нелепым выводам, которые всё равно вынудили бы нас сделать дополнительные предположения” [5, стр. 265]. Для современной физики с её парадоксами апелляция к “физически нелепым выводам” не очень убедительна. Поэтому в качестве таких дополнительных предположений обычно постулируют однородность и изотропность физического пространства и времени [6], что равнозначно утверждению об инвариантности интервала.
Совершенно очевидно, что в отношении абстрактных состояний абстрактной динамической системы подобное обоснование неприемлемо. У нас нет оснований для веры в универсальность этих принципов по отношению к системам, чья эволюция не осуществляется в физическом пространстве.
В нашем случае инварианты преобразований систем отсчёта должны отражать лишь те свойства системы времени, которые обусловлены линейной упорядоченностью её состояний и конструкцией автомата – наблюдателя.
Одним из таких свойств системы времени является положительное приращение количеств повторяющихся состояний её подсистем ![]() , соответствующее направлению “стрелы времени”. Сравнивая между собой две квадратичные формы – квадрат суммы положительных приращений с одной стороны и сумму их квадратов с другой, получим следующее очевидное неравенство
, соответствующее направлению “стрелы времени”. Сравнивая между собой две квадратичные формы – квадрат суммы положительных приращений с одной стороны и сумму их квадратов с другой, получим следующее очевидное неравенство
 . (18)
. (18)
Умножив это неравенство на ![]() , с учётом принятых выше обозначений получим
, с учётом принятых выше обозначений получим
![]() , (19)
, (19)
где ![]() обозначен интервал в пространстве событий системы времени. Так как величины
обозначен интервал в пространстве событий системы времени. Так как величины ![]() и
и ![]() , характеризующие движение подсистемы относительно внешнего наблюдателя, не зависят от выбора объекта начала отсчёта внутренним наблюдателем, они и, определяемый ими интервал
, характеризующие движение подсистемы относительно внешнего наблюдателя, не зависят от выбора объекта начала отсчёта внутренним наблюдателем, они и, определяемый ими интервал ![]() , являются инвариантами преобразований систем отсчёта. Переходя в неравенстве (19) к дифференциалам и подставляя значения переменных согласно формулам (15), выразим интервал
, являются инвариантами преобразований систем отсчёта. Переходя в неравенстве (19) к дифференциалам и подставляя значения переменных согласно формулам (15), выразим интервал ![]() через приращения координат и времени, измеряемые внутренним наблюдателем
через приращения координат и времени, измеряемые внутренним наблюдателем
 , (20)
, (20)
где ![]()
![]() - симметрическая матрица, которая может быть отождествлена с метрическим тензором внутреннего пространства событий. При этом квадратичная форма (20) может рассматриваться в качестве Римановой метрики пространства событий.
- симметрическая матрица, которая может быть отождествлена с метрическим тензором внутреннего пространства событий. При этом квадратичная форма (20) может рассматриваться в качестве Римановой метрики пространства событий.
Осуществляя преобразование (17) во внутреннем пространстве событий с помощью матрицы ![]() , численно равной матрице
, численно равной матрице ![]() , получим для малой окрестности некоторого события
, получим для малой окрестности некоторого события ![]() такую систему координат, в которой интервал с точки зрения внутреннего наблюдателя выражается такой же квадратичной формой, как и с точки зрения внешнего
такую систему координат, в которой интервал с точки зрения внутреннего наблюдателя выражается такой же квадратичной формой, как и с точки зрения внешнего
 . (21)
. (21)
Следовательно, внутреннее пространство событий характеризуется локально псевдоевклидовой римановой метрикой с сигнатурой (+ - - -…), а модуль наибольшей скорости ![]() , изменения состояний в нём, ограничен универсальной постоянной, не зависящей от выбора системы отсчёта
, изменения состояний в нём, ограничен универсальной постоянной, не зависящей от выбора системы отсчёта
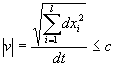 . (22)
. (22)
Предположим, что имеется некое множество подсистем, для которых коэффициенты ![]() , связывающие между собой результаты измерений внутреннего и внешнего наблюдателей в уравнениях (15), не зависят от координат и времени в некоторой локальной области пространства событий. Тогда вся эта область характеризуется метрикой (21).
, связывающие между собой результаты измерений внутреннего и внешнего наблюдателей в уравнениях (15), не зависят от координат и времени в некоторой локальной области пространства событий. Тогда вся эта область характеризуется метрикой (21).
Инвариантность интервала, предельной скорости изменения состояний, а также положительная определённость квадратичной формы (21), описывающей локальную метрику, являются необходимыми и достаточными условиями того, что преобразования (17) в локальной области пространства событий системы времени являются преобразованиями Лоренца. Подтверждением тому является общеизвестный вывод, исходя из перечисленных условий, этих преобразований для четырёхмерного пространства событий в специальной теории относительности, повторять который в данном случае не имеет смысла.
Заметим, что сами по себе математические выкладки при выводе преобразований Лоренца справедливы для любой размерности, но основания для их вывода в теории относительности черпались из эмпирических закономерностей движения физических тел в трёхмерном пространстве. Здесь же основанием для вывода преобразований Лоренца являются общие закономерности абстрактной цепи событий и не менее абстрактной конструкции автомата – наблюдателя. Следовательно, их действие распространяется на пространство событий абстрактной динамической системы произвольной размерности.
Теория относительности не объясняет причину ограничения скорости распространения сигналов (изменения состояний) в наблюдаемом пространстве. Ею постулируется без объяснения этот феномен как фундаментальное свойство физического пространства – времени. Видимо этим объясняются многочисленные попытки “преодолеть” предельную скорость в некоторых физических теориях. Однако, как видно из неравенства (18), ограничение скорости изменения состояний абстрактной динамической системы обусловлено направлением “стрелы времени” и не может быть преодолено никаким разумным способом, не требующим пересмотра оснований математики. Если бы такое “преодоление” было возможным, то это означало бы, что суммарное количество всех состояний на отрезке цепи событий больше чем количество событий. Иными словами, это означало бы, что система может оказываться в таких состояниях, которые не являются событиями, т.е. появление таких состояния в системе не увеличивает количества её событий, что противоречит общепринятой логической взаимосвязи понятий состояния и события. Если всё же допустить такие “фантомные” состояния, то можно заметить взаимосвязь между обратимостью времени и неограниченной скоростью их изменения. Действительно, если бы увеличение количества повторяющихся состояний могло сопровождаться уменьшением количества событий, то время в таком случае оказалось бы обращённым вспять. Количество событий уменьшалось бы с увеличением количества повторяющихся состояний системы времени. Так как время отождествляется с количеством событий, то из неравенства (18) уже нельзя было бы получить неравенство (19). Следовательно, скорость изменения состояний не имела бы ограничения. Таким образом, ограничение (22) предельной скорости изменения состояний указывает направление “кинематической стрелы времени”
Из преобразований Лоренца естественно вытекают все известные в специальной теории относительности пространственно – временные соотношения, характеризующие равномерное прямолинейное движение подсистем во внутреннем пространстве состояний системы времени. Однако интерес в данной работе представляет собой иное отношение, которым связаны между собой характеристики этого движения с распределением относительных частот повторений одинаковых состояний соответствующих подсистем в цепи событий. Этим отношением устанавливается соответствие между результатами наблюдений внешнего и внутреннего наблюдателей.
Запишем уравнения (10) дважды. Один раз для наблюдателя, связанного с одним объектом начала отсчёта, а второй раз для наблюдателя, связанного с другим.
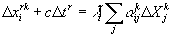 , (23)
, (23)
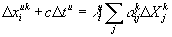 . (24)
. (24)
То, что под знаком суммы в обоих уравнениях все величины попарно равны, следует из тождественности самой себе подсистемы, наблюдаемой в обоих случаях одним и тем же наблюдателем. Сравнивая эти уравнения, найдём
 . (25)
. (25)
Вследствие инвариантности интервала имеем также
 . (26)
. (26)
Из этих двух уравнений, как показано А. Эйнштейном [7], достаточно просто выводятся преобразования Лоренца на ![]() - той координатной оси. Там же показано, что величина
- той координатной оси. Там же показано, что величина
 . (27)
. (27)
представляет собой относительную скорость движения подсистем при такой ориентации координатных осей в пространстве, что вектор скорости ![]() направлен вдоль
направлен вдоль ![]() - той координатной оси (
- той координатной оси (![]() ). Так как относительное движение подсистем рассматривается по отношению к одному и тому же наблюдателю, то величины
). Так как относительное движение подсистем рассматривается по отношению к одному и тому же наблюдателю, то величины ![]() и
и ![]() , входящие в выражения для
, входящие в выражения для ![]() и
и ![]() можно считать равными друг другу. Это соответствует выбору одинаковых масштабов в рассматриваемых системах отсчёта. Поэтому в (27) они взаимно сокращаются, и относительная скорость подсистем
можно считать равными друг другу. Это соответствует выбору одинаковых масштабов в рассматриваемых системах отсчёта. Поэтому в (27) они взаимно сокращаются, и относительная скорость подсистем ![]() и
и ![]() выражается через относительные частоты повторений их одноимённых состояний в цепи событий
выражается через относительные частоты повторений их одноимённых состояний в цепи событий
 . (28)
. (28)
Самое замечательное в этой формуле то, что относительная скорость движения подсистемы во внутреннем многомерном пространстве системы времени отображает распределение её состояний в цепи событий и не зависит от параметров, характеризующих конструкцию наблюдателя. Из этого следует, что разные внутренние наблюдатели, “не договариваясь заранее”, одинаково отображают кинематику собственного мира. А этим, в свою очередь, обусловлена возможность взаимной пространственно – временной синхронизация поведения автоматов – наблюдателей, что является предпосылкой образования в системе времени их коллективных сообществ.
Будем считать, что наблюдатель отображает относительное движение подсистемы траекторией точки относительно системы декартовых координат ![]() в пространстве состояний размерности
в пространстве состояний размерности ![]() . Из формулы (28) известна относительная скорость движения подсистем вдоль одной координатной оси при условии, что относительно других осей движение отсутствует. Следовательно, для того чтобы иметь возможность воспользоваться ею, необходимо рассматривать движение изображающей точки как совокупность движений
. Из формулы (28) известна относительная скорость движения подсистем вдоль одной координатной оси при условии, что относительно других осей движение отсутствует. Следовательно, для того чтобы иметь возможность воспользоваться ею, необходимо рассматривать движение изображающей точки как совокупность движений ![]() систем координат
систем координат ![]() , каждая из которых скользит относительно предшествующей точно в направлении одной оси. В этом случае
, каждая из которых скользит относительно предшествующей точно в направлении одной оси. В этом случае ![]() является скоростью движения системы координат
является скоростью движения системы координат![]() относительно системы координат
относительно системы координат![]() . Частные движения относительно различных систем отсчёта должны быть приведены к одной системе отсчёта
. Частные движения относительно различных систем отсчёта должны быть приведены к одной системе отсчёта ![]() . Рассмотрим решение этой задачи для двумерного случая, а затем обобщим его на системы любой размерности. Пусть на плоскости задана система декартовых координат
. Рассмотрим решение этой задачи для двумерного случая, а затем обобщим его на системы любой размерности. Пусть на плоскости задана система декартовых координат ![]() . Параллельно плоскости движется платформа, с которой скреплена система координат
. Параллельно плоскости движется платформа, с которой скреплена система координат ![]() . Оси координат систем
. Оси координат систем ![]() и
и ![]() взаимно параллельны. Движение платформы осуществляется в направлении оси
взаимно параллельны. Движение платформы осуществляется в направлении оси ![]() со скоростью
со скоростью ![]() . По платформе движется изображающая точка параллельно оси
. По платформе движется изображающая точка параллельно оси ![]() . Скорость её движения относительно платформы равна
. Скорость её движения относительно платформы равна ![]() (см. рис. 3). Требуется найти вектор скорости движения изображающей точки
(см. рис. 3). Требуется найти вектор скорости движения изображающей точки ![]() в системе координат
в системе координат ![]() .
.
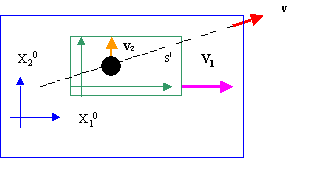
Рис. 3
Согласно известным в специальной теории относительности соотношениям компонента вектора скорости изображающей точки ![]() равна скорости
равна скорости ![]() , а ортогональная ей компонента
, а ортогональная ей компонента ![]() определяется формулой
определяется формулой
![]()
 . (29)
. (29)
Для решения данной задачи нам потребовалось разложить сложное движение точки в системе координат ![]() на сумму простых движений относительно
на сумму простых движений относительно ![]() и
и ![]() . При этом результат оказывается зависим от того, какой последовательностью простых движений представляется искомое сложное движение. Изменив эту последовательность в рассматриваемом примере, получим
. При этом результат оказывается зависим от того, какой последовательностью простых движений представляется искомое сложное движение. Изменив эту последовательность в рассматриваемом примере, получим
 (30)
(30)
Рассмотрим некоторые численные примеры.
Так как оба вида представления движения совершенно равноправны и в распределении состояний цепи событий не содержится информация о предпочтительном выборе того или иного из них, приходится допускать, что в общем случае одному конкретному распределению состояний цепи событий соответствует два представления её скорости во внутреннем двумерном пространстве состояний. Пусть в некоторый момент времени ![]() по часам внутреннего наблюдателя подсистема отображается им в пространстве состояний точкой M0. Дальнейшая эволюция траектории её равномерного движения, соответствующая примеру 1, показана на рис. 4.
по часам внутреннего наблюдателя подсистема отображается им в пространстве состояний точкой M0. Дальнейшая эволюция траектории её равномерного движения, соответствующая примеру 1, показана на рис. 4.

Рис. 4
Угол “размывания” траектории при одном и том же отношении ![]() и
и ![]() тем больше, чем больше значения составляющих скорости движения подсистемы. В предельном случае этот угол равен
тем больше, чем больше значения составляющих скорости движения подсистемы. В предельном случае этот угол равен ![]() (пример 2). Но относительно заданного объекта начала отсчёта существуют взаимно ортогональные оси, в направлении которых траектории не “размываются” (пример 3). Эти направления образуют систему взаимно ортогональных координат, связанную с данным объектом начала отсчёта, и структурируют внутреннее пространство системы времени. “Размывание” траектории подсистемы свидетельствует об увеличении её энтропии. Система взаимно ортогональных “неразмывающихся” траекторий соответствует группе движений с неизменной энтропией. Следовательно, можно предположить, что эти траектории являются экстремалями функционала, пропорционального энтропии системы, образующими во внутреннем пространстве особую (эквиэнтропийную) систему координат. Отображая цепь событий подсистемы во внутреннем пространстве системы времени описанным выше способом, мы получаем её траекторию именно в этой особой системе координат, связанной с объектом начала отсчёта.
(пример 2). Но относительно заданного объекта начала отсчёта существуют взаимно ортогональные оси, в направлении которых траектории не “размываются” (пример 3). Эти направления образуют систему взаимно ортогональных координат, связанную с данным объектом начала отсчёта, и структурируют внутреннее пространство системы времени. “Размывание” траектории подсистемы свидетельствует об увеличении её энтропии. Система взаимно ортогональных “неразмывающихся” траекторий соответствует группе движений с неизменной энтропией. Следовательно, можно предположить, что эти траектории являются экстремалями функционала, пропорционального энтропии системы, образующими во внутреннем пространстве особую (эквиэнтропийную) систему координат. Отображая цепь событий подсистемы во внутреннем пространстве системы времени описанным выше способом, мы получаем её траекторию именно в этой особой системе координат, связанной с объектом начала отсчёта.
Рассмотренный двумерный случай достаточно просто распространяется на любое число измерений
 (31)
(31)
В случае ![]() измерений наибольшее количество возможных представлений скорости равно
измерений наибольшее количество возможных представлений скорости равно ![]() .
.
Полученный результат позволяет по-новому взглянуть на общеизвестный парадокс “близнецов”. Если движение в пространстве осуществляется по замкнутому контуру не строго по направлениям, указываемым в каждой его точке осями эквиэнтропийной системы координат, то энтропия движущегося объекта к моменту возврата в исходную точку возрастёт соответственно скорости и маршруту движения. Поэтому, не смотря на релятивистское сокращение времени, действительный возраст движущегося объекта, определяемый приростом его энтропии, может оказаться даже больше возраста объекта, от которого начиналось и которым закончилось движение. Более того, его траектория может быть настолько “размыта” к моменту возврата, что распознать вернувшегося “близнеца”, томящийся в ожидании брат будет просто не в состоянии. Следовательно, в подобном случае актуальной становится проблема “эквиэнтропийной” навигации в пространстве.
Формулы (28), (31) открывают возможность численного интроспективного анализа временных рядов, образованных последовательностями сигналов, получаемых от исследуемых объектов. Результатом интроспективного анализа временного ряда является релятивистское представление порождающей его динамической системы ансамблем траекторий подсистем в её внутреннем многомерном пространстве состояний. Метод численного интроспективного анализа сводится к следующим операциям.
Исследование подобных моделей в самых различных областях знаний могут помочь выявить ранее не известные внутренние причины наблюдаемых процессов и явлений.
Обратным к задаче интроспективного анализа является интроспективный синтез временных рядов. Пусть в наблюдаемой внутренним наблюдателем области пространства известны усреднённые траектории множества подсистем некоторой динамической системы относительно эквиэнтропийных координат этого пространства (задача построения такой системы координат при заданном распределении подсистем в пространстве требует отдельного исследования, не предусмотренного объёмом и содержанием данной статьи). Требуется найти усреднённое распределение состояний в соответствующей цепи событий.
Разобьём интервал времени наблюдения на малые промежутки, в пределах которых допустимо считать проекции ![]() относительной скорости движения
относительной скорости движения ![]() - той подсистемы на координатные оси внутреннего пространства состояний постоянными.
- той подсистемы на координатные оси внутреннего пространства состояний постоянными.
Подставляя известные значения ![]() в (31) и задавшись порядком перечисления координатных осей, найдём значения
в (31) и задавшись порядком перечисления координатных осей, найдём значения ![]() . Подставляя эти значения в (28), получим систему
. Подставляя эти значения в (28), получим систему ![]() уравнений. В этих уравнениях будем считать известными отношения
уравнений. В этих уравнениях будем считать известными отношения ![]() , характеризующие объект начала отсчёта. Решение системы уравнений (29) при известных
, характеризующие объект начала отсчёта. Решение системы уравнений (29) при известных ![]() и
и ![]() даёт искомое распределение
даёт искомое распределение ![]() состояний
состояний ![]() - той подсистемы на синтезируемом отрезке цепи событий.
- той подсистемы на синтезируемом отрезке цепи событий.
ВЫВОДЫ
Список литературы