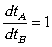Discussions. The answers to questions and remarks
Session of the scientific seminar on temporology, November 13, 2001
(below are made references to the papers given in References to
Section II “Research Program”).
1. What do you mean by the dynamical inhomogeneity of time? When does this phenomenon appear?
Answer. Let us consider the motion of a classical point particle
under the action of a force field in the inertial reference frames
 and
and  , moving relative to each other. The Cartesian coordinates connected
with the reference frames are assumed for definiteness to be oriented
in such a manner that the
, moving relative to each other. The Cartesian coordinates connected
with the reference frames are assumed for definiteness to be oriented
in such a manner that the  -axes of the frame
-axes of the frame
 are parallel to the
are parallel to the 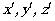 -axes of the frame
-axes of the frame  , the
, the  -axis and the
-axis and the  -axis coincide with each other, and the
reference frame
-axis coincide with each other, and the
reference frame  moves with a velocity
moves with a velocity  relative to the
relative to the  -frame along the
-frame along the  -axis. Denote by
-axis. Denote by  the length of a path section in a vicinity
of a point
the length of a path section in a vicinity
of a point  in the reference frame
in the reference frame  , which the particle covers for the time
, which the particle covers for the time  , and by
, and by
 and
and  the corresponding
quantities relating to the reference system
the corresponding
quantities relating to the reference system  . The quantities
. The quantities  and
and  are connected with each other by equality [33,34]:
are connected with each other by equality [33,34]:
 |
(1) |
where
 |
(2) |
 is the
is the  -component of the particle velocity
-component of the particle velocity  in the
in the  -frame at the instant of time
-frame at the instant of time  . As is seen from (1), if
. As is seen from (1), if
 , the quantity
, the quantity  depends not only on
depends not only on  , but also on the instant of time
, but also on the instant of time
 , that is the different instants of time on the
time axis prove to be physically non-equivalent. Therein lies the essence of the
phenomenon of local dynamical inhomogeneity of time. The dynamical inhomogeneity
of time means that the course of time in a vicinity of point
, that is the different instants of time on the
time axis prove to be physically non-equivalent. Therein lies the essence of the
phenomenon of local dynamical inhomogeneity of time. The dynamical inhomogeneity
of time means that the course of time in a vicinity of point  in the reference frame
in the reference frame  changes as compared to the
course of time in the frame
changes as compared to the
course of time in the frame  . As a measure of the
change in the course of time at a point one may use the ratio (see (1))
. As a measure of the
change in the course of time at a point one may use the ratio (see (1)) |
(3) |
Obviously, the dynamical inhomogeneity of time arises provided that
 , i.e. at
, i.e. at 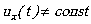 .
.2. Why can the force be considered as a reason of the dynamical inhomogeneity of time?
Answer. As can be seen from (2) and (3), if during some interval of time the particle moves
with a constant velocity ( ), i.e. by inertia, then on this
time interval
), i.e. by inertia, then on this
time interval
 |
that is the different instances of time are physically equivalent. Thus, the dynamical inhomogeneity of time is conditioned by the change in particle’s velocity, i.e. it is caused by the action of a force on particle.
3. Let us assume that the force 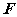 is such that
is such that
 . In this case
. In this case 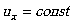 and thus by virtue of (2) and (3) the course of time is constant, contrary
to the statement made above that force is the reason for changing the course of time.
and thus by virtue of (2) and (3) the course of time is constant, contrary
to the statement made above that force is the reason for changing the course of time.
Answer. The reasoning above is erroneous for the following reason. According to the
relativistic equations of motion, if  , then
, then
 , but
, but  . From equality
. From equality
 |
it follows that .
4. What is meant by the change of the course of time along the trajectory of motion of particle in the same inertial reference frame? What quantity may serve as a measure of change of the course of time in this case?
Answer. Let us explain, first of all, what the constancy of the course of time
along the particle’s trajectory means. Let a dot particle move with constant
velocity ( ) relative to an inertial reference frame
) relative to an inertial reference frame
 . Obviously, by virtue of the constancy of particle’s
velocity, the particle passes the path sections
. Obviously, by virtue of the constancy of particle’s
velocity, the particle passes the path sections  and
and
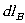 of equal length (
of equal length ( )
, situated in a vicinity of points
)
, situated in a vicinity of points  and
and  lying on the trajectory, for equal intervals of time:
lying on the trajectory, for equal intervals of time:
 |
(4) |
where
 |
The condition (4), which is carried out for any points
 and
and
 lying on the trajectory, expresses itself the constancy
of the course of time along the trajectory of motion of free particle. Evidently,
in the case of free particle the condition of the (4) type is carried out in any inertial
reference frame. This means that for free particle the course of time along the trajectory
does not vary with time in any inertial reference frame.
lying on the trajectory, expresses itself the constancy
of the course of time along the trajectory of motion of free particle. Evidently,
in the case of free particle the condition of the (4) type is carried out in any inertial
reference frame. This means that for free particle the course of time along the trajectory
does not vary with time in any inertial reference frame.If the particle moves relative to an inertial reference frame under the action of an external force, the situation essentially changes because of changing the velocity of the particle with time (
 ). Even if in the reference frame
). Even if in the reference frame

 |
(5) |
and, hence, in this reference frame the condition (4) is carried out (i.e. in the
 -frame the course of time is constant), in any other
inertial reference frame
-frame the course of time is constant), in any other
inertial reference frame  , moving relative to
, moving relative to
 , the course of time will change along the trajectory
as it follows from (1) and (2). An example of the force field, in which the flow of time
along the trajectory is constant, is homogeneous magnetic field: a charged particle moves
in this field with the velocity submitting to condition (5) (see [33,34]).
, the course of time will change along the trajectory
as it follows from (1) and (2). An example of the force field, in which the flow of time
along the trajectory is constant, is homogeneous magnetic field: a charged particle moves
in this field with the velocity submitting to condition (5) (see [33,34]).Before introducing a measure of change of the course of time along trajectory in the same inertial reference frame, we shall notice, that the course of time along trajectory may change only as a result of the action on particle of a force field, when the velocity of the particle varies from point to point. If the force field is absent (the particle moves with constant velocity), there is no reason for changing the course of time.
Let us pass from the inertial reference frame
 , in which
an external force operates on the particle, in such a reference frame
, in which
an external force operates on the particle, in such a reference frame 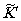 , in which the action of external force is completely compensated for by force of inertia at
that point of space at which the particle is placed. In the reference frame
, in which the action of external force is completely compensated for by force of inertia at
that point of space at which the particle is placed. In the reference frame
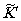 , the particle is in the state of imponderability, that
is it is free. The reference frame
, the particle is in the state of imponderability, that
is it is free. The reference frame 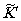 is quasi-inertial:
in some vicinity of the point, at which the particle is in the state of imponderability,
the reference frame
is quasi-inertial:
in some vicinity of the point, at which the particle is in the state of imponderability,
the reference frame 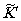 behaves as inertial. As in the
state of imponderability there is no force influence on the particle and, thus, there
is no reason for changing the course of time, the course of the proper time of particle
should be constant. Choosing identical intervals of proper time
behaves as inertial. As in the
state of imponderability there is no force influence on the particle and, thus, there
is no reason for changing the course of time, the course of the proper time of particle
should be constant. Choosing identical intervals of proper time  and
and 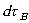 , corresponding to points
, corresponding to points  and
and  lying on particle’s trajectory, and taking into account
the relationship
lying on particle’s trajectory, and taking into account
the relationship |
(6) |
from equality
 |
(7) |
one can derive [37]:
 |
(8) |
where
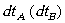 is the time interval in the reference frame
is the time interval in the reference frame
 , corresponding to proper time of the particle
, corresponding to proper time of the particle
 in the reference frame
in the reference frame 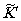 when the particle moves along the
when the particle moves along the
trajectory in a vicinity of point |
 |
. It is the quantity |
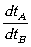 |
(8) that characterizes the |
 in comparison
with the course of time in a vicinity of point
in comparison
with the course of time in a vicinity of point  . The
course of time along the trajectory of motion of particle in some inertial reference
frame is constant, if
. The
course of time along the trajectory of motion of particle in some inertial reference
frame is constant, if  for any two points
for any two points
 and
and  lying on the
trajectory. As is seen from (8), the course of time along trajectory varies with varying
the particle’s velocity, i.e. in the presence of an external field acting on the particle
(the force influence is the reason for changing the course of time in the same inertial
reference frame).
lying on the
trajectory. As is seen from (8), the course of time along trajectory varies with varying
the particle’s velocity, i.e. in the presence of an external field acting on the particle
(the force influence is the reason for changing the course of time in the same inertial
reference frame).For the time intervals  and
and  the particle covers the path sections of length
the particle covers the path sections of length
 and and 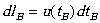 |
(9) |
respectively. By virtue of (8) and (9) one can obtain:
 |
(10) |
The ratio |
 |
(10) takes account of the change in the course of time at points |
 |
and |
 . . |
The condition |
 |
yields (see.(8)): |
|
5. The dynamical inhomogeneity of time seems to be an artefact resulting from an alternative and confusing definition of time in the systems of reference moving relative to each other, which does not change the equations, but allows one to dream of controlling time.
Answer. In my papers, there is no new definition of time different from the definition
given by the special theory of relativity (STR). The crux of the problem is that the force
in relativistic mechanics is not only the reason of acceleration of particle in an inertial
reference frame, but also the reason of change of the course of time along particle’s
trajectory. This is the main physical content of the STR.
6. What is called in the article the change in the course of time represents a trivial dependence of time intervals, during which the particle covers the path sections of identical length, upon velocity of particle on these path sections: with changing the particle’s velocity the lengths of these intervals change.
Answer. This statement is wrong. The mistake is caused by the wrong understanding
of the sense of quantities  and
and  in (8). The quantities above have no sense of time intervals during which the particle covers identical
distances in the vicinities of points
in (8). The quantities above have no sense of time intervals during which the particle covers identical
distances in the vicinities of points  and
and  (see equalities (10)). These quantities have the following meaning: they are those time
intervals which correspond to the identical intervals of proper time of the particle being
in the state of imponderability. To establish, whether the course of time along the
trajectory of particle in a force field changes, it is necessary to compare the course
of time when the particle moves freely (i.e. under conditions when there is obviously
no reason for changing the course of time) with that in the presence of a force influence
on the particle. It is from such a comparison that the formula (8) for the relative course
of time between points
(see equalities (10)). These quantities have the following meaning: they are those time
intervals which correspond to the identical intervals of proper time of the particle being
in the state of imponderability. To establish, whether the course of time along the
trajectory of particle in a force field changes, it is necessary to compare the course
of time when the particle moves freely (i.e. under conditions when there is obviously
no reason for changing the course of time) with that in the presence of a force influence
on the particle. It is from such a comparison that the formula (8) for the relative course
of time between points  and
and  is derived.
is derived.
It should be emphasized that, when the particle moves freely, quantity 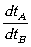 (8) is
always equal to 1, whereas when moving under the action of a force field, generally speaking,
(8) is
always equal to 1, whereas when moving under the action of a force field, generally speaking,
 . Last inequality points to the dependence of the flow of time on
the state of motion of the particle in force field, i.e. it testifies to the occurrence
of the physical properties of time. This result is of fundamental importance as it is
indicative of the feasibility of controlling the course of time.
. Last inequality points to the dependence of the flow of time on
the state of motion of the particle in force field, i.e. it testifies to the occurrence
of the physical properties of time. This result is of fundamental importance as it is
indicative of the feasibility of controlling the course of time.
7. What is the magnitude of the change in the course of time?
Answer. If the particle moves with the velocity small in comparison with that of
light ( 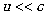 ), the change of the course of time is relativistically
small (it is of the order of
), the change of the course of time is relativistically
small (it is of the order of
 |
). |
8. What is meant physically by the change of the course of time in various areas of space in inertial reference frame? Is it possible to observe this effect?
Answer. From the physical point of view, the change of the course of time in one
area of space in comparison with the other means that the time scale in one area differs
from that in the other. The content of the paper consists in the proof that the time scale
along the trajectory of motion of particle depends upon the force influence on the particle.
This phenomenon is quite observable, and it should be taken into account because, without
regard for it, wrong expressions can be received both for the intervals of time between
physical events and for the distances between points at which these events occur (see
formula (10)).
9. One would think that the equality
 |
(11) |
which follows from the Lorentz transformations, points to the existence of the dynamical inhomogeneity of spatial coordinates similar to the inhomogeneity of time. Is such an interpretation correct?
Answer. As is seen from (11), the distance  , traversed by a particle in the
, traversed by a particle in the  -frame, depends not
only on the distance
-frame, depends not
only on the distance  , which the particle traverses
in the
, which the particle traverses
in the  -frame, but also on the instant of time
-frame, but also on the instant of time
 . This dependence cannot be treated, however, as
a manifestation of the dynamical inhomogeneity of spatial coordinates. Formula (11)
is a trivial consequence of kinematics: it expresses the simple fact that the distance
traversed by particle depends on its velocity, which may change with time (as a result
of the action of a force). Really, in classical mechanics, on the basis of the Galilean
transformations, we have successively:
. This dependence cannot be treated, however, as
a manifestation of the dynamical inhomogeneity of spatial coordinates. Formula (11)
is a trivial consequence of kinematics: it expresses the simple fact that the distance
traversed by particle depends on its velocity, which may change with time (as a result
of the action of a force). Really, in classical mechanics, on the basis of the Galilean
transformations, we have successively:
|
From this it follows that
 |
Up to the factor
 last formula coincides with (11).
In the case of relativistic mechanics we have analogously:
last formula coincides with (11).
In the case of relativistic mechanics we have analogously: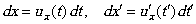 . . |
From here, using the velocity addition law and the Lorentz transformations for time, we arrive at formula (11).
Thus, as distinct from spatial coordinates, time in relativistic mechanics may be
deformed (i.e. time scale may change) under the action of an external force. It should
be emphasized that the active role of time in dynamics is due to the dynamical principle:
the latter is formulated in terms of time, not of spatial coordinates.
10. It would be desirable to elucidate the physical content of the notions “the physical properties of time” and “the physical properties of space”. What are the distinction and similarity between them?
Answer. I shall begin with the answer to the second part of the question. Common to
the properties mentioned above is that they are due to the dependence of time and spatial
characteristics of physical systems upon material processes occurring in them, while
distinctions are associated with the fact that time coordinate stands out in relation to
spatial coordinates from both geometrical and physical points of view (see [37]).
The physical properties of time signify the dependence of the course of time in some area
of space on the character of the physical processes occurring in this area. The reason of
the change of the course of time is the force field acting on a system.
By the physical properties of space is meant the fact that the spatial area, in which a
force field acts, turns to a physical medium having the capability to interact directly
with other particles.
It should be emphasized that because of the indissoluble connection between time and space
the occurrence of physical properties of space inevitably leads to the occurrence of
physical properties of time.
11. It is well known that the existence of the dependence of the course of time on gravitational field is substantiated in the general theory of relativity (GТR) . What is new in your work?
Answer. First of all, I shall make a quotation from [43] (see p. 303): “Already in
the special theory of relativity the flow of true time is different for the clocks moving
relative to each other. In the general theory of relativity the true time flows in different
ways also at different points of space in the same reference frame. This means that the
interval of proper time between two events occurring at some point of space and the interval
of time between the events taking place simultaneously with them at the other point of
space, generally speaking, are different from each other“. As “the gravitational field
is nothing but the change of the space-time metrics”([43], p. 313), one can assert,
apparently, that the change of the course of time is due, from the point of view of the
GTR, to the change of the 4-dimensional space metrics.
In the approach being developed, the gravitational field is considered as an ordinary force
field and the motion of particle is assumed to occur in the pseudo-Euclidean space-time.
The formulas received (see [37], and also formulas (8) and (9) from Section II) describe
the change of the course of time in an arbitrary force field at different points of space
in the same inertial reference frame. According to the results received, the change in the
course of time in a force field is by no means connected with the change of the space-time
metrics. It is caused by the action of the force field on a particle in inertial reference
frame and follows directly from the dynamical principle underlying relativistic mechanics.
12. The general theory of relativity predicts the red shift of spectral lines in gravitational field. Is there anything new about the shift of spectral lines in your theory?
Answer. As is seen from our results, the shift of spectral lines in gravitational
field is connected not to the change of the space-time metrics, but to that the gravitational
field is a force field. According to our approach, force is the reason of the change in the
course of time and, hence, the reason of the shift of spectral lines of atoms (the case in
point is merely that part of the shift which has a bearing on the change in the course of
time).
It should be emphasized that, from the point of view of quantum electrodynamics, the shift
of spectral lines of atoms is caused by interaction of atoms with force fields. This
interaction results in the occurrence of the energy level shifts of atoms and, hence, is the
reason of the shift of spectral lines. Evidently, the energy level shifts contain a
component connected with the change of the course of time, and its magnitude can be
calculated by our formulas.
If the force field is gravitational, the picture should remain the same: the shift of a
spectral line of atom, caused by the gravitational field, should consist of two
components - one of them is connected with the change of the course of time in gravitational
field and the other has no bearing on this change.
13. What is the basic result of your research on the problem of time?
Answer. The basic result is that the strict proof is given of the Kozyrev hypothesis
about the existence of physical properties of time, and a general relationship is received
connecting the course of time on one path section of a particle moving in a force field with
the course of time on the other in the same inertial reference frame. Briefly, basic
conclusion may be formulated as follows [37]: in relativistic mechanics, the force acting
on a particle in an inertial reference frame is the reason of change of the course of time
along the particle’s trajectory.