1) Анонсирование будущего доклада: Левич А.П. (Levich A.P.) (This email address is being protected from spambots. You need JavaScript enabled to view it.) "Моделирование времени-пространства открытых систем: строение, размерность, арифметизация".

Замысел работы – предложить модель, в которой течение времени и пространственное вместилище моделируемых систем оказываются не внешними по отношению к модели параметрами, а её конструктами. Также не хотелось бы без достаточных оснований вводить аналитический аппарат математики: комплексные или действительные числа, размерности и топологию многообразий и т.п. Выражаясь лапидарно, частицы – это не корпускулы, а излучающие нечто источники. Постулирую существование двух форм материи: 1) субстрата, состоящего из частиц, и 2) субстанций, состоящих из дискретных элементов. Представлю частицу парой (Q, f), где Q – источник или сток субстанции, а f – шлейф из испущенных источником (поглощенных стоком) элементов субстанции (позволю себе для краткости изложения в дальнейшем говорить только об источниках, подразумевая, что сток определен как "источник противоположного знака"). Совокупность нескольких частиц называю системой. Совокупность шлейфов этих частиц называю метаболическим пространством системы, а элементы субстанции – точками этого пространства. Подчеркну, что, согласно определению, "настоящие" элементы пространства – это не точки, а шлейфы субстанции. Части метаболического пространства могут не содержать источники частиц, но они никогда не пусты, так как "состоят" из материальной субстанции – шлейфов частиц. Состоянию метаболического пространства наиболее адекватно соответствует не термин "вакуум" (в переводе – пустое пространство), а его греческий антоним "пленум" (который буквально переводится как "непустое пространство"). Отмечу, что в модели и частицы, и пространство есть открытые по отношению к субстанциям, а не изолированные объекты мира. Допускаю существование субстанций нескольких типов. Они представляют собой несводимые друг к другу, невзаимозаменимые сущности и порождают различные типы зарядов, взаимодействий и метаболических времен. Метаболическое пространство может объединять шлейфы субстанций различных типов. Назову метаболической размерностью D метаболического пространства количество типов субстанций в составляющих метаболическое пространство шлейфах. Постулирую существование эталонного расстояния 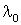между соседними точками шлейфов эталонной субстанции и назову его шагом эталона измерения расстояний, подразумевая, что выполняется принцип императивности для эталона расстояния: шаги между всеми соседними точками эталона измерения расстояний одинаковы. Назову эталонной метаболической линейкой тройку, состоящую из эталона измерения расстояний, метаболического счетчика элементов и шага . 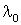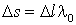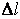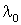Назову расстоянием по эталонной метаболической линейке (метаболическим расстоянием) между двумя точками метаболического пространства эталонной субстанции число , где – количество точек метаболического пространства между указанными точками и – шаг эталона измерения расстояний. Каждому из d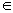D измерений ("осей координат") времени-пространства можно сопоставить пару чисел (t_d,x_d), задаваемых количеством t_d элементов субстанции типа d, появившихся с момента начала отсчета, и расстоянием x_d от начала отсчета, измеренному линейкой типа d. Таким образом, в D-мерном времени-пространстве имеется D пар координат (t_d,x_d) – D временных и D пространственных. Возникает соблазн эксплицировать пару (t_d,x_d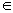), d D комплексным числом x_d+ i_d t_d. Насколько оправдана такая экспликация, подразумевающая очень специфический закон умножения: (t₁ , x₁)∙(t₂ , x₂) = (x₁t₂ + x₂t₁ , x₁x₂ - t₁t₂)? Существуют ли физические или методологические обоснования такого закона? Следует ли в случае "комплексификации" измерений пространства считать мнимые единицы i_d различными и само пространство – гиперкомплексным? Более естественным для метаболического подхода видится эйлерово представление комплексных чисел ρe^iφ, где обобщенные координаты (ρ, φ) можно интерпретировать в физических терминах – длина, фаза, энергия, время, действие… Очередной вопрос метаболического подхода – может ли закон умножения (в декартовой или полярной форме) быть введен "естественным" образом, а не формальным заимствованием из алгебры? Согласно модели, частица "состоит" из источника и шлейфа элементов субстанции, образующего вместе со шлейфами других частиц метаболическое пространство. И, если источник "точечен", то шлейф распределен во всем пространстве, точнее, объединение шлейфов и есть само пространство. Таким образом, частица как целое локализована не в "точке", а во всем пространстве. То же относится к временной протяжности частицы. Другими словами, частицы нелокальны как во времени, так и в пространстве, так как существуют не в отдельные, а во все моменты во всех точках своего времени-пространства. Частицы в метаболической модели нестационарны: шлейфы частиц "растут" (или "сокращаются") в каждый момент метаболического времени (точнее, этот "рост" и есть по определению "метаболическое время"). 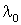О "росте" шлейфов можно сказать и как об их "распространении" в метаболическом пространстве (если в качестве системы отсчета принять не элементы субстанции, а их источник), а о самом шлейфе с чередованием бытия и небытия своих элементов с шагом и периодом можно говорить как о "метаболической волне", обладающей как пространственной, так и временной плотностью. Метаболическое пространство было определено как совокупность шлейфов частиц. Это определение можно переформулировать как "объединение метаболических волн". В этом смысле метаболическое пространство приобретает "динамическую структуру", которая усложняет представления о дискретности пространства. С одной стороны, оно "состоит" из дискретных элементов субстанции, но, с другой стороны, ни в какой момент времени и ни в какой области пространства не существует какой-либо стационарной дискретной структуры. Порождающие пространство шлейфы субстанций некоторых типов могут быть неравномерны. Это означает, что среди длительностей и/или расстояний между соседними элементами в них есть не равные друг другу (при измерении с помощью периода и шага шлейфа эталонной субстанции). Такая неравномерность может быть интерпретирована как неоднородность метаболического времени-пространства, приводящая, согласно геометрической концепции, к взаимодействиям частиц. (A.P. Levich. Generating Flows and a Substantional Model of Space-Time // Gravitation and Cosmology. 1995. V.1. №3. Pp. 237-242. A.P.Levich. Paradigms of natural science and substantial temporology // The Nature of Time: Geometry, Physics and Perception. Edited by Rosolino Buccheri, Metod Saniga, and William Mark Stuckey. Kluwer Academic Publishers: Dordrecht / Boston / London (published in cooperation with NATO Scientific Affairs Division), 2003. Pp. 427-435. Левич А.П. Модель частиц, порождающая пространство-время и становление // Основания физики и геометрии. М.: РУДН, 2008. С. 153-188. А.П.Левич. Моделирование природных референтов времени: метаболическое время и пространство // На пути к пониманию феномена времени: конструкции времени в ес­тествознании. Часть 3. Методология. Физика. Биология. Математика. Теория систем. М.: Прогресс-Традиция, 2009. С. 259-337.) Комментировать

2) Доклад: Морозов А.Н. "Неравновесные состояния и необратимые процессы".

 

Презентация Download Связанные материалы - не заполнять

• Презентация: Morozov A.N. Неравновесные состояния и необратимые процессы (Скачать) // Категории: Презентации 2011 г. [размещено на сайте 13.09.2015]

Комментировать